MATH 152: Calculus 2, SET8 EXAMPLES [Belmonte, 2018] 6 Applications of Integration. 5.5 The Substitution Rule. 6.2 Volumes. 6.1 Areas Between Curves
|
|
|
- Elizabeth Little
- 6 years ago
- Views:
Transcription
1 MATH 5: Calculus, SET8 EXAMPLES [Belmote, 8] 6 Applicatios of Itegratio 55 The Substitutio Rule [48/6] Evaluate the itegral t + dt by makig the substitutio u = t + [48/8] Evaluate x e x3 dx via the Substitutio Rule 3 [49/] Same as precedig for sec x 4 [49/3] Evaluate ta x dx 5 [49/38] Evaluate dt cos t + ta t z z 3 + dz 6 [49/48] Evaluate x 3 x + dx 3 dx 7 [49/63] Evaluate the defiite itegral 3 ( + x) 8 [49/68] Evaluate 4 x +x dx 9 [49/77] Evaluate (x + 3) 4 x dx by writig it as the sum of two itegrals ad the usig symmetry [49/78] Evaluate x x 4 dx by makig a substitutio ad iterpretig the resultig itegral i terms of a area 6 Areas Betwee Curves [434/6] Fid the area bouded by the curve y = six ad the lies y = x, x = π/, ad x = π [434/] Fid the area bouded by 4x + y = ad x = y 3 [434/8] Fid the area bouded by y = x ad x y = 4 [434/4] Fid the area bouded by y = cos x ad y = cos x for x π 5 [435/3] Fid the area of the regio eclosed by the curves x y = ad y = x, where x + x 9 x 6 [435/36] Evaluate the itegral 3x x dx ad iterpret it as the area of a regio 9 [436/5] The rates at which rai fell, i iches per hour, i two differet locatios t hours after the start of a storm are f (t) = 73t 3 t +t + 6 ad g(t) = 7t 5t + Compute the area betwee their graphs for t ad iterpret your result i this cotext [436/56] Fid the area of the regio bouded by the parabola y = x, its taget lie at (,), ad the x-axis 6 Volumes [446/3] Fid the volume of the solid obtaied by rotatig the regio bouded by y = x, y =, x = 5, about the x-axis [446/6] Fid the volume of the solid obtaied by rotatig the regio bouded by x = y, x =, y = 4, about the y-axis 3 [446/9] Fid the volume of the solid obtaied by rotatig the regio bouded by y = x, x = y, about the y-axis 4 [446/] Fid the volume of the solid obtaied by rotatig the regio bouded by y = x 3, y =, x =, about y = 3 5 [446/5] Fid the volume of the solid obtaied by rotatig the regio bouded by y = x 3, y =, x =, about x = 6 [447/35] Fid approximate x-coordiates of the poits of itersectio of the curves y = l ( x 6 + ) ad y = 3 x 3 The fid the approximate volume of the solid obtaied by rotatig about the x-axis the regio boud by the curves 7 [447/38] Use a CAS to fid the exact volume of the solid obtaied by rotatig the regio boud by the curves y = x, y = xe x/ about y = 3 8 [447/46] Cosider a profile view of a bird s egg (a) A model for its shape is obtaied by rotatig about the x-axis the regio uder the graph of f (x) = ( ax 3 + bx + cx + d ) x, x Use a CAS to fid the volume of such a egg (b) For a red-throated loo, a = 6, b = 4, c =, ad d = 54 Graph f ad fid the volume of a egg of this species 9 [448/55] The base of a solid S is a elliptical regio with boudary curve 9x + 4y = 36 Cross-sectios perpedicular to the x-axis are isosceles right triagles with hypoteuse i the base Fid the volume of S [448/6] The base of a solid S is the regio eclosed by y = x ad the x-axis Cross-sectios perpedicular to the y-axis are quarter-circles Fid the volume of S 7 [435/4] Graph the regio betwee the curves y = e x ad y = x 4 Compute its area correct to 5 decimal places 8 [435/48] The widths w (i meters) of a kidey-shaped swimmig pool were measured at -meter itervals as idicated i the table below Use the Midpoit Rule to estimate the area of the pool x w
2 63 Volumes by Cylidrical Shells [453/] Let S be the solid obtaied by rotatig the regio bouded by y = x(x ) ad y = about the y-axis Fid the volume of S via cylidrical shells [459/6] The table shows values of a force fuctio f (x), where x is measured i meters ad f (x) i ewtos Use the Midpoit Rule to estimate the work doe by the force i movig a object from x = 4 to x = x f (x) [459/7] A force of lb is required to hold a sprig stretched 4i beyod its atural legth How much work (i ft-lb) is doe i stretchig it from it atural legth to 6i beyod its atural legth? 4 [459/9] Suppose that J of work is eeded to stretch a sprig from its atural legth of 3cm to a legth of 4cm [454/6] Use the method of cylidrical shells to fid the volume geerated by rotatig the regio bouded by y = 4x x, y = x, about the y-axis 3 [454/3] Use the method of cylidrical shells to fid the volume geerated by rotatig the regio bouded by x = + (y ), x =, about the x-axis 4 [454/8] Use the method of cylidrical shells to fid the volume geerated by rotatig the regio bouded by y = x, x = y, about x = 5 5 [454/3] Fid the volume of the solid obtaied by rotatig the regio bouded by the curves y = ±cos 4 x, π x π, about x = π 6 [454/7] Use the Midpoit Rule with = 5 to estimate the volume obtaied by rotatig about the y-axis the regio uder the curve y = + x 3, x (a) How much work is eeded to stetch the sprig from 35cm to 4cm? (b) How far beyoud its atural legth will a force of 3N keep the sprig stretched? 5 [459/] If 6J of work is eeded to stetch a sprig from cm to cm ad aother J is eeded to stretch it from cm to 4cm, what is the atural legth of the sprig? 6 [459/5] A cable that weighs lb/ft is used to lift 8lb of coal up a mie shaft 5ft deep Fid the total work doe 7 [459/] A circular swimmig pool has a diameter of 4ft, the sides are 5ft high, ad the depth of the water is 4ft How much work is required to pump all of the water out over the side? (The weight desity of water is δ = 65lb/ft 3 ) 8 [459/3] A tak is full of water, the mass desity of which is ρ = kg/m 3 Fid the work required to pump the water out of the spout (Gravitatioal acceleratio is g = 98m/s ) 7 [454/34] Fid the approximate x-coordiates of the poits of itersectio of the curves y = e six ad y = x 4x + 5 The estimate the volume of the solid obtaied by rotatig about the y-axis the regio eclosed by these curves 8 [454/36] Use a CAS to fid the exact volume of the solid obtaied by rotatig the regio bouded by y = x 3 six, y =, x π, about x = 9 [455/39] The regio bouded by y x = ad y = is rotated about the x-axis Fid the volume of the resultig solid by ay method you wish 9 [459/4] Same as #8 with the spherical tak depicted below [455/4] The regio bouded by x + (y ) = is rotated about the y-axis Fid the volume of the resultig solid by ay method you wish 64 Work [458/3] A variable force of F (x) = 5x pouds moves a object alog a straight lie whe it is x feet from the origi Calculate the work doe i movig the object from x = ft to x = ft [46/8] Same as #9, but with the tak half full of oil that has mass desity ρ = 9kg/m 3
3 MATH 5: Calculus, SET8 EXAMPLES [Belmote, 8] 7 Techiques of Itegratio 7 Itegratio by Parts [476/] Evaluate the itegral x lxdx usig itegratio by parts with u = lx ad dv = xdx [476/8] Evaluate the itegral t siβt dt 3 [476/] Evaluate the itegral x ta xdx 4 [476/4] Evaluate the defiite itegral ( x + ) e x dx 5 [476/3] Evaluate the defiite itegral 3 arcta(/x) dx r 3 6 [477/34] Evaluate dr 4 + r 7 [477/4] First make a substitutio ad the use itegratio by arcsi(lx) parts to evaluate the itegral dx x 8 [477/46] Evaluate the idefiite itegral x sixdx, the graph both the itegrad ad its atiderivative (take C = ) 9 [477/58] Fid the area of the regio bouded by y = x e x ad y = xe x [477/64] Use the method of cylidrical shells to fid the volume geerated by rotatig the regio bouded by the curves y = e x, x =, ad y = 3 about the x-axis 7 Trigoometric Itegrals 73 Trigoometric Substitutio [49/] Use the trigoometric substitutio x = taθ x 3 to evaluate the itegral x + 4 dx 3 x [49/6] Evaluate the itegral dx 36 x /3 dx 3 [49/6] Evaluate /3 x 5 9x 4 [49/8] Evaluate 5 [49/8] Evaluate dx ((ax) b ) 3/ x + (x x + ) dx π/ cost 6 [49/3] Evaluate + si t dt 7 [49/34] Fid the area of the regio bouded by the hyperbola 9x 4y = 36 ad the lie x = 3 8 [49/38] Fid the volume of the solid obtaied by rotatig about the lie x = the regio uder the curve y = x x, x 9 [49/4] The parabola y = x divides the circular disk x + y 8 ito two parts Fid the areas of both parts [49/4] A charged rod of legth L produces a electric field L a λb at poit P(a,b) give by E (P) = dx a 4πε (x + b 3/ ) where λ is the charge desity per uit legth o the rod ad ε is the free space permittivity (see figure) Evaluate the itegral to obtai a expressio for the electric field E (P) [484/] Evaluate the itegral si 3 θ cos 4 θ dθ [484/] Evaluate the itegral π si t cos 4 t dt 3 [484/6] Evaluate the itegral π/4 sec 6 θ ta 6 θ dθ 4 [484/8] Evaluate the itegral ta 5 x sec 3 xdx 5 [484/3] Evaluate π/4 ta 4 xdx 6 [485/36] Evaluate π/ π/4 cot3 xdx 7 [485/4] Evaluate siθ si6θ dθ 8 [485/46] Evaluate π/4 cos4θ dθ 9 [485/58] Fid the area of the regio bouded by the curves y = tax, y = ta x, x π/4 [485/64] Fid the volume obtaied by rotatig the regio bouded by the curves y = secx, y = cosx, x π/3, about the lie y = 74 Itegratio of Ratioal Fuctios by Partial Fractios [5/4] Give the form of the partial fractio decompositio (PFD) of these expressios [I MATLAB, automatically determie the PFDs usig the partfrac commad!] (a) x4 x 3 + x + x x x + (b) x x 3 + x + x
4 [5/] Evaluate the itegral x 4 x 5x + 6 dx x 3 + 4x + x 3 [5/6] Evaluate x 3 + x dx x 4 [5/3] Evaluate x + 4x + 3 dx 5 [5/4] Make a substitutio to express the itegrad as a ratioal fuctio the evaluate + 3 x dx 6 [5/48] Same as #5 for 7 [5/5] Same as #5 for six cos x 3cosx dx e x (e x )(e x + ) dx 8 [5/6] Use t = ta ( ) x, cosx = t, six = t +t dx = +t dt to evaluate π/ π/3 + six cosx dx +t ad 9 [5/64] Fid the area of the regio uder the curve y = / ( x 3 + x ), x [5/66] Fid the volume of the resultig solid if the regio uder the curve y = / ( x + 3x + ) from x = to x = is rotated about (a) the x-axis ad (b) the y-axis 78 Improper Itegrals [534/] Which of the followig itegrals are improper? Why? (a) π/4 taxdx (b) π taxdx (c) dx (d) e x3 dx x x [534/6] Determie whether the itegral 4 dx is + x coverget or diverget If coverget, compute its value 3 [534/] Same as # for 4 [534/6] Same as # for 5 [534/8] Same as # for 5 6 [535/34] Same as # for r dr siθe cosθ dθ dv v + v 3 w w dw π/ cosθ 7 [535/38] Same as # for dθ siθ 8 [535/56] Evaluate x dx by usig a trigoometric x 4 substitutio, the splittig the iterval of itegratio i the resultig itegral 9 [535/58] Fid the values of p for which e x(lx) p dx coverges ad evaluate the itegral for those values of p [536/8] Fid the value of C for which the improper itegral x x + C dx coverges The evaluate the itegral 3x + for this value of C
5 MATH 5: Calculus, SET8 EXAMPLES [Belmote, 8] Parametric Equatios Curves Defied by Parametric Equatios [645/4] Sketch the curve x = e t +t, y = e t t, t State how the curve is traversed as t icreases [645/6] Sketch the curve x = 3t +, y = t + 3 State how the curve is traversed as t icreases Elimiate the parameter to fid a Cartesia equatio of the curve 3 [645/8] Sketch the curve x = sit, y = cost, t π State how the curve is traversed as t icreases Elimiate the parameter to fid a Cartesia equatio of the curve 4 [645/5] Sketch the curve x = t, y = lt State how the curve is traversed as t icreases Elimiate the parameter to fid a Cartesia equatio of the curve 5 [645/8c] Sketch the curve x = sit, y = si(t + sit) 6 [647/3] Graph the curves y = x 3 4x ad x = y 3 4y ad fid their poits of itersectio to two decimal places 7 [647/34] Cosider the ellipse x a + y b = (a) Give parametric equatios for x ad y i terms of t (b) Graph the ellipse for a = 3 ad b =,, 4, 8 (c) How does the ellipse s shape chage as b icreases? 8 [648/45] The positio of oe particle at time t is give by x = 3sit, y = cost, t π ad the positio of a secod particle is give by x = 3 + cost, y = + sit, t π (a) Graph the paths of both particles How may poits of itersectio are there? Fid ad plot them (b) Are ay of these poits of itersectio collisio poits? I other words, are the particles ever at the same place at the same time? If so, fid ay collisio poits (c) Repeat (a) ad (b) if the path of the secod particle is x 3 = 3 + cost, y 3 = + sit, t π 9 [648/47] Ivestigate the family of curves defied by the parametric equatios x = t, y = t 3 ct How does the shape chage as c icreases? Illustrate by graphig members of the family for c =,,, [648/5] Graph several members of the family of curves x = sit + sit, y = cost + cost, t π, where is a positive iteger What features do they have i commo? What happes as icreases? Use =,, 3, 4, 5 Calculus with Parametric Curves [655/3] Fid a equatio of the taget lie to the curve x = t 3 +, y = t 4 +t, for t = [655/7] Fid parametric ad Cartesia equatios for the taget lie to the curve x = + lt, y = t +, at (,3) 3 [655//] Fid dy/dx ad d y/dx give x = t +, y = t +t For which values of t is the curve cocave upward? 4 [655/7] Fid the poits o the curve x = t 3 3t, y = t 3, where the taget is horizotal or vertical Illustrate 5 [655/6] Graph the curve x = cost, y = sit + si t to discover where the curve crosses itself The fid equatios of both tagets at that poit Illustrate with a graph 6 [655/3] Fid the area eclosed by the curve x = t t, y = t ad the y-axis 7 [656/46] Graph the curve x = cost + l ( ta t), y = sit, π 4 t 3π 4 ad fid its arc legth 8 [656/48] Fid the legth of the loop of the curve x = 3t t 3, y = 3t 9 [656/6] Fid the surface area obtaied by rotatig the curve x = t + t, y = 8 t, t 3, about the x-axis [657/66] Fid the surface area obtaied by rotatig the curve x = e t t, y = 4e t/, t, about the y-axis 3 Polar Coordiates [666/] Sketch the regio i the plae whose polar coordiates satisfy r 3, π 6 < θ < 5π 6 [666/6] Fid a Cartesia equatio for the polar curve r = 4secθ Illustrate 3 [667//6] Fid a polar equatio for the Cartesia equatio x y = 4 Illustrate 4 [667/5] Fid a polar equatio for the Cartesia equatio ( x + y ) 3 = 4x y, the sketch the curve 5 [667/6] Fid the taget lie to the curve r = + cosθ at θ = π/3 Illustrate 6 [667/6] Fid the poits o the curve r = 3cosθ where the taget lie is horizotal or vertical Sketch 7 [668/68] Graph the hippopede r = 8si θ 8 [668/7] Graph the valetie curve r = taθ cotθ 9 [668/7] Graph the curve r = + cos(9θ/4) Beauty, eh? [668/74] Graph the curve r = siθ Fid the y-coordiate of the highest poits o the curve
6 4 Areas ad Legths i Polar Coordiates [673/8] Fid the area of the regio betwee the curve r = lθ, θ π ad the origi [673/] Sketch the curve r = cosθ ad fid the area it ecloses 9 [68/5] A cross-sectio of a parabolic reflector is show i the figure The bulb is located at the focus F ad the opeig at the focus is cm (a) Fid a equatio of the parabola (b) Fid CD, the diameter of the opeig that is cm from the vertex 3 [673//] Fid the area of the regio eclosed by oe loop of the curve r = si5θ 4 [673/4] Fid the area of the regio that lies iside the curve r = si θ ad outside the curve r = Illustrate 5 [673/6] Fid the area of the regio that lies iside the curve r = + cosθ ad outside the curve r = cosθ Illustrate 6 [673/3] Fid the area of the regio that lies iside both r = 3 + cosθ ad r = 3 + siθ Illustrate 7 [673/36] Fid the area of betwee a large loop ad the eclosed small loop of r = + cos 3θ Illustrate 8 [673/4] Fid all poits of itersectio of the curves r = cos3θ ad r = si3θ Illustrate 9 [673/46] Fid the legth of r = 5 θ, θ π Illustrate [673/49] Fid the legth of the curve r = cos 4 (θ/4) Graph 5 Coic Sectios [68/8] Fid the vertex, focus, ad directrix of the parabola x 6x 3y + 38 = ad sketch its graph [68/4] Fid the vertices ad foci of the ellipse x + 36y = 5 ad sketch its graph 3 [68//8] Fid a equatio of the ellipse depicted The fid its foci 4 [68/4] Fid the vertices, foci, ad asymptotes of the hyperbola 9y 4x 36y 8x = 4 ad sketch its graph 5 [68/3] Idetify the type of coic sectio whose equatio is x x + y 8y + 7 = Fid vertices ad foci; graph 6 [68/3] Fid a equatio for the parabola with focus (,) ad directrix y = 6 Sketch 7 [68/4] Fid a equatio for the ellipse with foci (, ) ad (8, ) ad vertex (9, ) Sketch 8 [68/44] Fid a equatio for the hyperbola with foci (,±5) ad vertices (,±) Sketch [68/54] Fid a equatio for the slated ellipse with foci (,) ad (,) ad major axis of legth 4 Graph 6 Coic Sectios i Polar Coordiates [688/] Write a polar equatio of a parabola with the focus at the origi ad directrix x = 3 Sketch the curve [688/4] Write a polar equatio of a hyperbola with the focus at the origi, eccetricity 3 ad directrix x = 3 Illustrate 3 [688/6] Write a polar equatio of a ellipse with the focus at the origi, eccetricity 3/5 ad directrix r = 4cscθ Graph 4 [688/] Let r = + siθ (a) Fid the eccetricity (b) Idetify the coic (c) Give a equatio of the directrix (d) Sketch the coic 5 [688/] Same as #4 for r = 6 [688/4] Same as #4 for r = 7 [688/6] Same as #4 for r = 5 4cosθ 3 3siθ 4 + 3cosθ 8 [688/8] Graph the coic r = 4/(5 + 6cosθ) alog with its directrix Additioally graph the coic obtaied by rotatig this curve about the origi through a agle π/3 9 [688/5] The orbit of Mars aroud the su is a ellipse with eccetricity 93 ad the semimajor axis 8 8 km Fid a polar equatio for the orbit [688/3] Jupiter s orbit has eccetricity 48 ad the legth of the major axis is 56 9 km Fid a polar equatio for the orbit
7 MATH 5: Calculus, SET8 EXAMPLES [Belmote, 8] Ifiite Sequeces & Series Sequeces [74/8] List the first 5 terms of the sequece a = ( )! + [74/4] Fid a formula for the geeral term a of the sequece { 4,, 4, 6, 64,}, assumig that the patter for the first few terms cotiues 3 [74/6] Determie whether the sequece a = + (86) coverges or diverges If it coverges, fid the limit 4 [74/36] Same as #3 for a = ( ) + 5 [74/5] Same as #3 for a = ( ) 6 [74/6] Graph the sequece a =! to decide whether it is coverget or diverget 7 [75/64] Defie a sequece by a = c, a + = 4 a, where c is a costat Determie if the sequece is coverget or diverget i each of the two cases (a) a = ad (b) a = 8 [75/77] Determie whether the sequece a = 3 e is icreasig, decreasig, or ot mootoic Is it bouded? 9 [75/8] A recursive sequece is give by a =, a + = + a (a) Show that {a } is a icreasig sequece ad bouded above by 3 Apply the Mootoic Sequece Theorem (MST) to show that lim a exists (b) Fid the limit [75/8] Show that the recursive sequece defied by a =, a + = 3 a satisfies < a ad is decreasig Deduce that it coverges ad fid its limit Series [75/4] Calculate the sum of the series a whose partial sums are s = 4 + [75/8] Calculate the first eight partial sums of the series ( ) to four decimal places Does it appear that the! series is coverget or diverget? 3 [75/] Fid the first te partial sums of cos to four decimal places Graph both the sequece of terms {a } ad the sequece of partial sums {s } o the same plot Does it appear that the series is coverget or diverget? If it is coverget, fid the sum If it is diverget, explai why 4 [76/4] Same as #3 for ( si ) si + 5 [76/8] Determie whether the geometric series is coverget or diverget If it is coverget, fid its sum 6 [76/4] Same as #5 for 7 [76/6] Same as #5 for = 3 + ( ) [76/8] Is the series coverget or diverget? If it is coverget, fid its sum 9 [76/35] Same as #8 for k= (si)k [76/36] Same as #8 for +(/3) [76/44] Determie whether the series l + is coverget or diverget by expressig it as a telescopig sum If it is coverget, fid its sum [76/45] Same as # for 3 ( + 3) 3 [76/56] Express the umber as a ratio of itegers (The digits uder the bar repeat) 4 [76/6] Fid the values of x for which = ( 4) (x 5) coverges Fid the sum of the series for those values of x 5 [77/64] We have see that the harmoic series is a diverget series whose terms approach Show that ( l + ) is aother series with this property 6 [77/66] Use MATLAB s partial fractio commad partfrac to fid a coveiet expressio for the th partial sum of the series The fid the sum of the series + 4 =3 7 [77/75] Fid the value of c if = ( + c) = 8 [77/76] Fid the value of c such that = ec = 9 [78/8] Suppose that a with a is kow to be coverget Show that (/a ) diverges [78/85] If a is coverget ad b is diverget, show that the series (a + b ) is diverget (Argue by cotradictio) 3 The Itegral Test ad Estimates of Sums [75/4] Use the Itegral Test (IT) to determie whether the series 3/ is coverget or diverget
8 [75/8] Same as # for e 3 3 [76/4] Determie if this p-series coverves or diverges 4 [76/] Same as # for 5 [76/6] Same as # for = [76/8] Explai why the Itegral Test ca t be used to cos determie whether the series is coverget + 7 [76/3] Fid the values of p for which the series is coverget 8 [76/36] Cosider the series ζ (4) = Exercise 76/35 i the textbook l p 4 = π4 give i 9 (a) Fid the th partial sum s of the series Estimate the error i usig it to approximate the sum of the series (b) Use iformatio from the Remaider Estimate for the Itegral Test i a maer similar to Example 6 i the text to give a improved estimate of the sum (c) Compare your estimate i part (b) with ζ (4) (d) Fid a value of so that s is withi 5 of the sum 9 [76/4] Cosider the series (a) Show that it is coverget (l ) (b) Fid a upper boud for the error i the approximatio s s (c) What is the smallest value of such that this upper boud is less tha 5? (d) Fid s for this value of [77/46] Fid all values of c for which the series coverges ( c ) + 4 The Compariso Tests (CT) [73/] Suppose that a ad b are series with positive terms ad b is kow to be diverget (a) If a > b for all, what ca you say about a? Why? (b) If a < b for all, what ca you say about a? Why? [73/6] Determie whether the series diverges Explai why 3 [73/] Same as # for 4 [73/8] Same as # for 5 [73/4] Same as # for 6 [73/3] Same as # for k= (k ) ( k ) (k + )(k + 4) ! 3 coverges or + 7 [73/36] Use the first terms to approximate the sum of the series 3 Estimate the error [73/38] For what values of p does the series coverge? = 9 [73/44] Show that if a > ad a is coverget, the l( + a ) is coverget p l [73/46] If a ad b are both coverget series with positive terms, is it true that a b is also coverget? Why? 5 Alteratig Series [736/4] Test the series l3 l4 + l5 l6 + l7 for covergece or divergece [736/8] Same as # for 3 [736/4] Same as # for 4 [736/6] Same as # for 5 [736/] Same as # for 6 [736/] For the series ( ) + + ( ) arcta cos π ( ) ( + ) ( ) do the followig 8 (a) Graph both the sequece of terms ad the sequece of partial sums o the same plot (b) Use the graph to make a rough estimate of the sum of the series (c) The use the Alteratig Series Estimatio Theorem (ASET) to estimate the sum correct to 4 decimal places
9 7 [736/6] Cosider the series ( ) (a) Show that the series is coverget (b) How may terms do we eed to add i order to fid the sum of the series with a error < 5? (c) Compute this estimate of the sum 8 [736/8] Approximate the sum of the series correct to 4 decimal places 9 [736/3] For what values of p is the series coverget? [736/34] Same as #9 for = ( ) (l) p ( ) + 6 ( ) 6 Absolute Covergece ad the Ratio ad Root Tests ( ) [74/4] Determie whether the series 3 is absolutely + coverget (AC) or coditioally coverget (CC) [743/6] Same as # for ( ) [743/4] Use the Ratio Test to determie whether the series! is coverget or diverget 4 [743/] Same as #4 for ()! (!) 5 [743/6] Use the Root Test to determie whether the series ( ) is coverget or diverget 6 [743/34] Use ay test(s) to determie whether the series 5 is absolutely coverget (AC), coditioally + coverget (CC), or diverget (D) 7 [743/38] Same as #6 for = ( ) l 8 [743/44] For which positive itegers k is the series coverget? p (!) (k)! 9 [744/48] Compute the th partial sum as well as the actual sum of the series (Use MATLAB) [744/5] Aroud 9, the Idia mathematicia Sriivasa Ramauja discovered the formula π = (4)!( ) 98 = (!) William Gosper used this series i 985 to compute the first 7 millio digits of π (a) Verify that the series is coverget (b) How may correct decimal places of π do you get if you use just the first term of the series? What if you use the first two terms? 8 Power Series [75/6] Fid the radius of covergece R ad iterval of ( ) x covergece I of the power series [75/8] Same as # for 3 [75/] Same as # for 4 [75/] Same as # for 5 [75/8] Same as # for 6 [75/] Same as # for 7 [75/] Same as # for 8 [75/4] Same as # for 9 [75/6] Same as # for = = x x ( ) 5 x 8 (x + 6) (x ) 5 b l (x a) where b > x 4 6 () x (l) [75/34] Graph the first several partial sums s (x) of the series = x, together with the fuctio f (x) = /( x) o the same plot O what iterval do these partial sums appear to be covergig to f (x)? 9 Represetatio of Fuctios as Power Series [757/4] Fid a power series represetatio of f (x) = 5 4x ad determie its radius ad iterval of covergece [757/8] Same as # for f (x) = x x + 3
10 3 [757/] Same as # for f (x) = x + 3 x Start by + 3x + fidig the partial fractio decompositio of f (x) 4 [757/6] Same as # for f (x) = x ta ( x 3), but oly give the radius of covergece 5 [757/] Same as #4 for f (x) = x + x ( x) 3 6 [758/4] Cosider the fuctio f (x) = ta (x) (a) Fid a power series represetatio for f (x) (b) Graph f ad several partial sums s (x) together (c) What happes as icreases? ta x 7 [758/8] Evaluate the idefiite itegral dx as a x power series What is the radius of covergece? 8 [758/3] Use a power series to approximate the defiite itegral / arcta(x/) dx to six decimal places = ( ) x 9 [758/34] Show that the fuctio f (x) = is a ()! solutio of the differetial equatio f (x) + f (x) = [758/4] Cosider the geometric series = x (a) Fid the sum of the series (b) Fid sums of the series (c) Fid the sums of the series =, ad x, x < x for x < ad = ( )x for x <, Taylor & Maclauri Series [77/8] Fid the first four ozero terms of the Taylor series for f (x) = lx cetered at a = usig the defiitio [77/6] Fid the Maclauri series for f (x) = xcosx ad its radius of covergece 3 [77/4] Fid the Taylor series for f (x) = cosx cetered at a = π/ ad its radius of covergece 4 [77/4] Fid the Maclauri series for f (x) = x l ( + x 3) x six 5 [77/44] Same as #4 for f (x) = x 3 if x 6 if x = 6 [77/48] Fid the Maclauri series for f (x) = ta ( x 3) ad its radius of covergece The graph both f ad its first few Taylor polyomials o the same plot Commet 7 [77/56] Evaluate the idefiite itegral arcta ( x ) dx as a ifiite series 8 [77/58] Use series to approximate the defiite itegral si ( x 4) dx to four decimal places cosx 9 [77/6] Use series to evaluate the limit lim x + x e x [77/78] Fid the sum l + (l)! (l)3 3! Applicatios of Taylor Polyomials + [78/4] Fid the Taylor polyomial T 3 (x) for f (x) = six cetered at a = π/6 Graph them together [78/8] Same as #4 for f (x) = xcosx at a = 3 [78/] Same as #4 for f (x) = ta x at a = 4 [78/] Use a CAS to fid Taylor polyomials T (x) for f (x) = 3 + x cetered at a = for =,3,4,5 Graph them together 5 [78/6] Let f (x) = six, a = π/6, = 4, ad I = [, 3 π] (a) Approximate f by T (x) (b) Use Taylor s Iequality to estimate the approximatio f (x) T (x) o I (c) Check part (b): graph R (x) = f (x) T (x) o I 6 [78/] Same as #5 for f (x) = xlx, a =, = 3, ad I = [5, 5] 7 [78/4] Use iformatio from #5 to esimate si38 correct to 5 decimal places 8 [78/8] Estimate the rage of x for which the approximatio cosx x + 4 x4 is accurate to withi 5 9 [78/36] A uiformly charged disk has radius R ad surface charge desity σ The electric potetial V at poit P at a distace d alog ( the perpedicular cetral axis of the disk is d ) V = πk e σ + R d where k e is Coulomb s costat Show that V πk e R σ/d for large d (See diagram i text) [78/37] If a surveyor measures differeces i elevatio whe makig plas for a highway across a desert, correctios must be made for the curvature of the earth (See diagram i text) (a) If R is the radius of the earth ad L is the legth of the highway, show the correctio is C = R sec(l/r) R (b) Use a Taylor polyomial to show that C L R + 5L4 4R 3 (c) Compare the correctios give by the formulas i parts (a) ad (b) for a highway that is km log (Take the radius of the earth to be 637km) 4
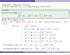
Taylor Series and Applications - (8.7)(8.8) b n!x # c" n for x # c " R.!x # c" # f %%!c" 2! T!x"! 1 # x # x2 2! # x3. 3! n!
 Taylor Series ad Applicatios - (8.7)(8.8). Taylor ad Maclauri Series: For a give fuctio f!x, how ca we fid its power series represetatio? If f has a power series represetatio at a umber a, that is, if
Taylor Series ad Applicatios - (8.7)(8.8). Taylor ad Maclauri Series: For a give fuctio f!x, how ca we fid its power series represetatio? If f has a power series represetatio at a umber a, that is, if
Test 4 Review. dy du 9 5. sin5 zdz. dt. 5 Ê. x 2 È 1, 3. 2cos( x) dx is less than using Simpson's. ,1 t 5 t 2. ft () t2 4.
 Name: Class: Date: ID: A Test Review Short Aswer. Fid the geeral solutio of the differetial equatio below ad check the result by differetiatio. dy du 9 u. Use the error formula to estimate the error i
Name: Class: Date: ID: A Test Review Short Aswer. Fid the geeral solutio of the differetial equatio below ad check the result by differetiatio. dy du 9 u. Use the error formula to estimate the error i
NTH, GEOMETRIC, AND TELESCOPING TEST
 NTH, GEOMETRIC, AND TELESCOPING TEST Sectio 9. Calculus BC AP/Dual, Revised 08 viet.dag@humbleisd.et /4/08 0:0 PM 9.: th, Geometric, ad Telescopig Test SUMMARY OF TESTS FOR SERIES Lookig at the first few
NTH, GEOMETRIC, AND TELESCOPING TEST Sectio 9. Calculus BC AP/Dual, Revised 08 viet.dag@humbleisd.et /4/08 0:0 PM 9.: th, Geometric, ad Telescopig Test SUMMARY OF TESTS FOR SERIES Lookig at the first few
Intro to Scientific Computing: Solutions
 Itro to Scietific Computig: Solutios Dr. David M. Goulet. How may steps does it take to separate 3 objects ito groups of 4? We start with 5 objects ad apply 3 steps of the algorithm to reduce the pile
Itro to Scietific Computig: Solutios Dr. David M. Goulet. How may steps does it take to separate 3 objects ito groups of 4? We start with 5 objects ad apply 3 steps of the algorithm to reduce the pile
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Math 10C Long Range Plans
 Math 10C Log Rage Plas Uits: Evaluatio: Homework, projects ad assigmets 10% Uit Tests. 70% Fial Examiatio.. 20% Ay Uit Test may be rewritte for a higher mark. If the retest mark is higher, that mark will
Math 10C Log Rage Plas Uits: Evaluatio: Homework, projects ad assigmets 10% Uit Tests. 70% Fial Examiatio.. 20% Ay Uit Test may be rewritte for a higher mark. If the retest mark is higher, that mark will
South Slave Divisional Education Council. Math 10C
 South Slave Divisioal Educatio Coucil Math 10C Curriculum Package February 2012 12 Strad: Measuremet Geeral Outcome: Develop spatial sese ad proportioal reasoig It is expected that studets will: 1. Solve
South Slave Divisioal Educatio Coucil Math 10C Curriculum Package February 2012 12 Strad: Measuremet Geeral Outcome: Develop spatial sese ad proportioal reasoig It is expected that studets will: 1. Solve
EVALUATION OF TRIGONOMETRIC FUNCTIONS
 EVALUATION OF TRIGONOMETRIC FUNCTIONS Whe first exposed to trigoometric fuctios i high school studets are expected to memorize the values of the trigoometric fuctios of sie cosie taget for the special
EVALUATION OF TRIGONOMETRIC FUNCTIONS Whe first exposed to trigoometric fuctios i high school studets are expected to memorize the values of the trigoometric fuctios of sie cosie taget for the special
Area As A Limit & Sigma Notation
 Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
Bezier curves. Figure 2 shows cubic Bezier curves for various control points. In a Bezier curve, only
 Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
9 x and g(x) = 4. x. Find (x) 3.6. I. Combining Functions. A. From Equations. Example: Let f(x) = and its domain. Example: Let f(x) = and g(x) = x x 4
 1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
WebAssign Lesson 6-1b Geometric Series (Homework)
 WebAssig Lesso 6-b Geometric Series (Homework) Curret Score : / 49 Due : Wedesday, July 30 204 :0 AM MDT Jaimos Skriletz Math 75, sectio 3, Summer 2 204 Istructor: Jaimos Skriletz. /2 poitsrogac alcet2
WebAssig Lesso 6-b Geometric Series (Homework) Curret Score : / 49 Due : Wedesday, July 30 204 :0 AM MDT Jaimos Skriletz Math 75, sectio 3, Summer 2 204 Istructor: Jaimos Skriletz. /2 poitsrogac alcet2
Math Section 2.2 Polynomial Functions
 Math 1330 - Sectio. Polyomial Fuctios Our objectives i workig with polyomial fuctios will be, first, to gather iformatio about the graph of the fuctio ad, secod, to use that iformatio to geerate a reasoably
Math 1330 - Sectio. Polyomial Fuctios Our objectives i workig with polyomial fuctios will be, first, to gather iformatio about the graph of the fuctio ad, secod, to use that iformatio to geerate a reasoably
Physics 11b Lecture #19
 Physics b Lecture #9 Geometrical Optics S&J Chapter 34, 35 What We Did Last Time Itesity (power/area) of EM waves is give by the Poytig vector See slide #5 of Lecture #8 for a summary EM waves are produced
Physics b Lecture #9 Geometrical Optics S&J Chapter 34, 35 What We Did Last Time Itesity (power/area) of EM waves is give by the Poytig vector See slide #5 of Lecture #8 for a summary EM waves are produced
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
Section 7.2: Direction Fields and Euler s Methods
 Sectio 7.: Directio ields ad Euler s Methods Practice HW from Stewart Tetbook ot to had i p. 5 # -3 9-3 odd or a give differetial equatio we wat to look at was to fid its solutio. I this chapter we will
Sectio 7.: Directio ields ad Euler s Methods Practice HW from Stewart Tetbook ot to had i p. 5 # -3 9-3 odd or a give differetial equatio we wat to look at was to fid its solutio. I this chapter we will
Mathematics and Art Activity - Basic Plane Tessellation with GeoGebra
 1 Mathematics ad Art Activity - Basic Plae Tessellatio with GeoGebra Worksheet: Explorig Regular Edge-Edge Tessellatios of the Cartesia Plae ad the Mathematics behid it. Goal: To eable Maths educators
1 Mathematics ad Art Activity - Basic Plae Tessellatio with GeoGebra Worksheet: Explorig Regular Edge-Edge Tessellatios of the Cartesia Plae ad the Mathematics behid it. Goal: To eable Maths educators
Recursive Procedures. How can you model the relationship between consecutive terms of a sequence?
 6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
Creating Exact Bezier Representations of CST Shapes. David D. Marshall. California Polytechnic State University, San Luis Obispo, CA , USA
 Creatig Exact Bezier Represetatios of CST Shapes David D. Marshall Califoria Polytechic State Uiversity, Sa Luis Obispo, CA 93407-035, USA The paper presets a method of expressig CST shapes pioeered by
Creatig Exact Bezier Represetatios of CST Shapes David D. Marshall Califoria Polytechic State Uiversity, Sa Luis Obispo, CA 93407-035, USA The paper presets a method of expressig CST shapes pioeered by
FURTHER INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
 Mathematics Revisio Guides More Trigoometric ad Log Itegrals Page of 7 MK HOME TUITION Mathematics Revisio Guides Level: AS / A Level AQA : C Edexcel: C OCR: C OCR MEI: C FURTHER INTEGRATION TECHNIQUES
Mathematics Revisio Guides More Trigoometric ad Log Itegrals Page of 7 MK HOME TUITION Mathematics Revisio Guides Level: AS / A Level AQA : C Edexcel: C OCR: C OCR MEI: C FURTHER INTEGRATION TECHNIQUES
Chapter 18: Ray Optics Questions & Problems
 Chapter 18: Ray Optics Questios & Problems c -1 2 1 1 1 h s θr= θi 1siθ 1 = 2si θ 2 = θ c = si ( ) + = m = = v s s f h s 1 Example 18.1 At high oo, the su is almost directly above (about 2.0 o from the
Chapter 18: Ray Optics Questios & Problems c -1 2 1 1 1 h s θr= θi 1siθ 1 = 2si θ 2 = θ c = si ( ) + = m = = v s s f h s 1 Example 18.1 At high oo, the su is almost directly above (about 2.0 o from the
The Nature of Light. Chapter 22. Geometric Optics Using a Ray Approximation. Ray Approximation
 The Nature of Light Chapter Reflectio ad Refractio of Light Sectios: 5, 8 Problems: 6, 7, 4, 30, 34, 38 Particles of light are called photos Each photo has a particular eergy E = h ƒ h is Plack s costat
The Nature of Light Chapter Reflectio ad Refractio of Light Sectios: 5, 8 Problems: 6, 7, 4, 30, 34, 38 Particles of light are called photos Each photo has a particular eergy E = h ƒ h is Plack s costat
1. Sketch a concave polygon and explain why it is both concave and a polygon. A polygon is a simple closed curve that is the union of line segments.
 SOLUTIONS MATH / Fial Review Questios, F5. Sketch a cocave polygo ad explai why it is both cocave ad a polygo. A polygo is a simple closed curve that is the uio of lie segmets. A polygo is cocave if it
SOLUTIONS MATH / Fial Review Questios, F5. Sketch a cocave polygo ad explai why it is both cocave ad a polygo. A polygo is a simple closed curve that is the uio of lie segmets. A polygo is cocave if it
PLEASURE TEST SERIES (XI) - 04 By O.P. Gupta (For stuffs on Math, click at theopgupta.com)
 wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Arithmetic Sequences
 . Arithmetic Sequeces COMMON CORE Learig Stadards HSF-IF.A. HSF-BF.A.1a HSF-BF.A. HSF-LE.A. Essetial Questio How ca you use a arithmetic sequece to describe a patter? A arithmetic sequece is a ordered
. Arithmetic Sequeces COMMON CORE Learig Stadards HSF-IF.A. HSF-BF.A.1a HSF-BF.A. HSF-LE.A. Essetial Questio How ca you use a arithmetic sequece to describe a patter? A arithmetic sequece is a ordered
It just came to me that I 8.2 GRAPHS AND CONVERGENCE
 44 Chapter 8 Discrete Mathematics: Fuctios o the Set of Natural Numbers (a) Take several odd, positive itegers for a ad write out eough terms of the 3N sequece to reach a repeatig loop (b) Show that ot
44 Chapter 8 Discrete Mathematics: Fuctios o the Set of Natural Numbers (a) Take several odd, positive itegers for a ad write out eough terms of the 3N sequece to reach a repeatig loop (b) Show that ot
Fundamentals of Media Processing. Shin'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dinh Le
 Fudametals of Media Processig Shi'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dih Le Today's topics Noparametric Methods Parze Widow k-nearest Neighbor Estimatio Clusterig Techiques k-meas Agglomerative Hierarchical
Fudametals of Media Processig Shi'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dih Le Today's topics Noparametric Methods Parze Widow k-nearest Neighbor Estimatio Clusterig Techiques k-meas Agglomerative Hierarchical
Polynomial Functions and Models. Learning Objectives. Polynomials. P (x) = a n x n + a n 1 x n a 1 x + a 0, a n 0
 Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
. Perform a geometric (ray-optics) construction (i.e., draw in the rays on the diagram) to show where the final image is formed.
 MASSACHUSETTS INSTITUTE of TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.161 Moder Optics Project Laboratory 6.637 Optical Sigals, Devices & Systems Problem Set No. 1 Geometric optics
MASSACHUSETTS INSTITUTE of TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.161 Moder Optics Project Laboratory 6.637 Optical Sigals, Devices & Systems Problem Set No. 1 Geometric optics
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Parabolic Path to a Best Best-Fit Line:
 Studet Activity : Fidig the Least Squares Regressio Lie By Explorig the Relatioship betwee Slope ad Residuals Objective: How does oe determie a best best-fit lie for a set of data? Eyeballig it may be
Studet Activity : Fidig the Least Squares Regressio Lie By Explorig the Relatioship betwee Slope ad Residuals Objective: How does oe determie a best best-fit lie for a set of data? Eyeballig it may be
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
The number n of subintervals times the length h of subintervals gives length of interval (b-a).
 Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
Spherical Mirrors. Types of spherical mirrors. Lecture convex mirror: the. geometrical center is on the. opposite side of the mirror as
 Lecture 14-1 Spherical Mirrors Types of spherical mirrors covex mirror: the geometrical ceter is o the opposite side of the mirror as the object. cocave mirror: the geometrical ceter is o the same side
Lecture 14-1 Spherical Mirrors Types of spherical mirrors covex mirror: the geometrical ceter is o the opposite side of the mirror as the object. cocave mirror: the geometrical ceter is o the same side
An (or ) is a sequence in which each term after the first differs from the preceding term by a fixed constant, called the.
 Sectio.2 Arithmetic Sequeces ad Series -.2 Arithmetic Sequeces ad Series Arithmetic Sequeces Arithmetic Series Key Terms: arithmetic sequece (arithmetic progressio), commo differece, arithmetic series
Sectio.2 Arithmetic Sequeces ad Series -.2 Arithmetic Sequeces ad Series Arithmetic Sequeces Arithmetic Series Key Terms: arithmetic sequece (arithmetic progressio), commo differece, arithmetic series
Project 2.5 Improved Euler Implementation
 Project 2.5 Improved Euler Implemetatio Figure 2.5.10 i the text lists TI-85 ad BASIC programs implemetig the improved Euler method to approximate the solutio of the iitial value problem dy dx = x+ y,
Project 2.5 Improved Euler Implemetatio Figure 2.5.10 i the text lists TI-85 ad BASIC programs implemetig the improved Euler method to approximate the solutio of the iitial value problem dy dx = x+ y,
( n+1 2 ) , position=(7+1)/2 =4,(median is observation #4) Median=10lb
 Chapter 3 Descriptive Measures Measures of Ceter (Cetral Tedecy) These measures will tell us where is the ceter of our data or where most typical value of a data set lies Mode the value that occurs most
Chapter 3 Descriptive Measures Measures of Ceter (Cetral Tedecy) These measures will tell us where is the ceter of our data or where most typical value of a data set lies Mode the value that occurs most
Integration: Reduction Formulas Any positive integer power of sin x can be integrated by using a reduction formula.
 Itegratio: Reductio Formulas Ay positive iteger power of si x ca be itegrated by usig a reductio formula. Prove that for ay iteger 2, si xdx = 1 si 1 x cos x + 1 si Solutio. Weuseitegratiobyparts. Let
Itegratio: Reductio Formulas Ay positive iteger power of si x ca be itegrated by usig a reductio formula. Prove that for ay iteger 2, si xdx = 1 si 1 x cos x + 1 si Solutio. Weuseitegratiobyparts. Let
Optimal Mapped Mesh on the Circle
 Koferece ANSYS 009 Optimal Mapped Mesh o the Circle doc. Ig. Jaroslav Štigler, Ph.D. Bro Uiversity of Techology, aculty of Mechaical gieerig, ergy Istitut, Abstract: This paper brigs out some ideas ad
Koferece ANSYS 009 Optimal Mapped Mesh o the Circle doc. Ig. Jaroslav Štigler, Ph.D. Bro Uiversity of Techology, aculty of Mechaical gieerig, ergy Istitut, Abstract: This paper brigs out some ideas ad
Convex hull ( 凸殻 ) property
 Covex hull ( 凸殻 ) property The covex hull of a set of poits S i dimesios is the itersectio of all covex sets cotaiig S. For N poits P,..., P N, the covex hull C is the give by the expressio The covex hull
Covex hull ( 凸殻 ) property The covex hull of a set of poits S i dimesios is the itersectio of all covex sets cotaiig S. For N poits P,..., P N, the covex hull C is the give by the expressio The covex hull
Ch 9.3 Geometric Sequences and Series Lessons
 Ch 9.3 Geometric Sequeces ad Series Lessos SKILLS OBJECTIVES Recogize a geometric sequece. Fid the geeral, th term of a geometric sequece. Evaluate a fiite geometric series. Evaluate a ifiite geometric
Ch 9.3 Geometric Sequeces ad Series Lessos SKILLS OBJECTIVES Recogize a geometric sequece. Fid the geeral, th term of a geometric sequece. Evaluate a fiite geometric series. Evaluate a ifiite geometric
The golden search method: Question 1
 1. Golde Sectio Search for the Mode of a Fuctio The golde search method: Questio 1 Suppose the last pair of poits at which we have a fuctio evaluatio is x(), y(). The accordig to the method, If f(x())
1. Golde Sectio Search for the Mode of a Fuctio The golde search method: Questio 1 Suppose the last pair of poits at which we have a fuctio evaluatio is x(), y(). The accordig to the method, If f(x())
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
UNIT 4 Section 8 Estimating Population Parameters using Confidence Intervals
 UNIT 4 Sectio 8 Estimatig Populatio Parameters usig Cofidece Itervals To make ifereces about a populatio that caot be surveyed etirely, sample statistics ca be take from a SRS of the populatio ad used
UNIT 4 Sectio 8 Estimatig Populatio Parameters usig Cofidece Itervals To make ifereces about a populatio that caot be surveyed etirely, sample statistics ca be take from a SRS of the populatio ad used
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
Civil Engineering Computation
 Civil Egieerig Computatio Fidig Roots of No-Liear Equatios March 14, 1945 World War II The R.A.F. first operatioal use of the Grad Slam bomb, Bielefeld, Germay. Cotets 2 Root basics Excel solver Newto-Raphso
Civil Egieerig Computatio Fidig Roots of No-Liear Equatios March 14, 1945 World War II The R.A.F. first operatioal use of the Grad Slam bomb, Bielefeld, Germay. Cotets 2 Root basics Excel solver Newto-Raphso
Name Date Hr. ALGEBRA 1-2 SPRING FINAL MULTIPLE CHOICE REVIEW #1
 Name Date Hr. ALGEBRA - SPRING FINAL MULTIPLE CHOICE REVIEW #. The high temperatures for Phoeix i October of 009 are listed below. Which measure of ceter will provide the most accurate estimatio of the
Name Date Hr. ALGEBRA - SPRING FINAL MULTIPLE CHOICE REVIEW #. The high temperatures for Phoeix i October of 009 are listed below. Which measure of ceter will provide the most accurate estimatio of the
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
The Graphs of Polynomial Functions
 Sectio 4.3 The Graphs of Polyomial Fuctios Objective 1: Uderstadig the Defiitio of a Polyomial Fuctio Defiitio Polyomial Fuctio 1 2 The fuctio ax a 1x a 2x a1x a0 is a polyomial fuctio of degree where
Sectio 4.3 The Graphs of Polyomial Fuctios Objective 1: Uderstadig the Defiitio of a Polyomial Fuctio Defiitio Polyomial Fuctio 1 2 The fuctio ax a 1x a 2x a1x a0 is a polyomial fuctio of degree where
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Chapter 11. Parametric Equations And Polar Coordinates
 Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
COMP 558 lecture 6 Sept. 27, 2010
 Radiometry We have discussed how light travels i straight lies through space. We would like to be able to talk about how bright differet light rays are. Imagie a thi cylidrical tube ad cosider the amout
Radiometry We have discussed how light travels i straight lies through space. We would like to be able to talk about how bright differet light rays are. Imagie a thi cylidrical tube ad cosider the amout
SD vs. SD + One of the most important uses of sample statistics is to estimate the corresponding population parameters.
 SD vs. SD + Oe of the most importat uses of sample statistics is to estimate the correspodig populatio parameters. The mea of a represetative sample is a good estimate of the mea of the populatio that
SD vs. SD + Oe of the most importat uses of sample statistics is to estimate the correspodig populatio parameters. The mea of a represetative sample is a good estimate of the mea of the populatio that
Recursive Estimation
 Recursive Estimatio Raffaello D Adrea Sprig 2 Problem Set: Probability Review Last updated: February 28, 2 Notes: Notatio: Uless otherwise oted, x, y, ad z deote radom variables, f x (x) (or the short
Recursive Estimatio Raffaello D Adrea Sprig 2 Problem Set: Probability Review Last updated: February 28, 2 Notes: Notatio: Uless otherwise oted, x, y, ad z deote radom variables, f x (x) (or the short
Cubic Polynomial Curves with a Shape Parameter
 roceedigs of the th WSEAS Iteratioal Coferece o Robotics Cotrol ad Maufacturig Techology Hagzhou Chia April -8 00 (pp5-70) Cubic olyomial Curves with a Shape arameter MO GUOLIANG ZHAO YANAN Iformatio ad
roceedigs of the th WSEAS Iteratioal Coferece o Robotics Cotrol ad Maufacturig Techology Hagzhou Chia April -8 00 (pp5-70) Cubic olyomial Curves with a Shape arameter MO GUOLIANG ZHAO YANAN Iformatio ad
Fast Fourier Transform (FFT) Algorithms
 Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
Consider the following population data for the state of California. Year Population
 Assigmets for Bradie Fall 2016 for Chapter 5 Assigmet sheet for Sectios 5.1, 5.3, 5.5, 5.6, 5.7, 5.8 Read Pages 341-349 Exercises for Sectio 5.1 Lagrage Iterpolatio #1, #4, #7, #13, #14 For #1 use MATLAB
Assigmets for Bradie Fall 2016 for Chapter 5 Assigmet sheet for Sectios 5.1, 5.3, 5.5, 5.6, 5.7, 5.8 Read Pages 341-349 Exercises for Sectio 5.1 Lagrage Iterpolatio #1, #4, #7, #13, #14 For #1 use MATLAB
Numerical Methods Lecture 6 - Curve Fitting Techniques
 Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Visualization of Gauss-Bonnet Theorem
 Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
Basic Optics: Index of Refraction
 Basic Optics: Idex of Refractio Deser materials have lower speeds of light Idex of Refractio = where c = speed of light i vacuum v = velocity i medium Eve small chages ca create differece i Higher idex
Basic Optics: Idex of Refractio Deser materials have lower speeds of light Idex of Refractio = where c = speed of light i vacuum v = velocity i medium Eve small chages ca create differece i Higher idex
AP B mirrors and lenses websheet 23.2
 Name: Class: _ Date: _ ID: A AP B mirrors ad leses websheet 232 Multiple Choice Idetify the choice that best completes the statemet or aswers the questio 1 The of light ca chage whe light is refracted
Name: Class: _ Date: _ ID: A AP B mirrors ad leses websheet 232 Multiple Choice Idetify the choice that best completes the statemet or aswers the questio 1 The of light ca chage whe light is refracted
CS Polygon Scan Conversion. Slide 1
 CS 112 - Polygo Sca Coversio Slide 1 Polygo Classificatio Covex All iterior agles are less tha 180 degrees Cocave Iterior agles ca be greater tha 180 degrees Degeerate polygos If all vertices are colliear
CS 112 - Polygo Sca Coversio Slide 1 Polygo Classificatio Covex All iterior agles are less tha 180 degrees Cocave Iterior agles ca be greater tha 180 degrees Degeerate polygos If all vertices are colliear
2) Give an example of a polynomial function of degree 4 with leading coefficient of -6
 Math 165 Read ahead some cocepts from sectios 4.1 Read the book or the power poit presetatios for this sectio to complete pages 1 ad 2 Please, do ot complete the other pages of the hadout If you wat to
Math 165 Read ahead some cocepts from sectios 4.1 Read the book or the power poit presetatios for this sectio to complete pages 1 ad 2 Please, do ot complete the other pages of the hadout If you wat to
1. The lines intersect. There is one solution, the point where they intersect. The system is called a consistent system.
 Commo Core Math 3 Notes Uit Day Systems I. Systems of Liear Equatios A system of two liear equatios i two variables is two equatios cosidered together. To solve a system is to fid all the ordered pairs
Commo Core Math 3 Notes Uit Day Systems I. Systems of Liear Equatios A system of two liear equatios i two variables is two equatios cosidered together. To solve a system is to fid all the ordered pairs
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
MATH 1020 WORKSHEET 10.1 Parametric Equations
 MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
Name Date Hr. ALGEBRA 1-2 SPRING FINAL MULTIPLE CHOICE REVIEW #2
 Name Date Hr. ALGEBRA - SPRING FINAL MULTIPLE CHOICE REVIEW # 5. Which measure of ceter is most appropriate for the followig data set? {7, 7, 75, 77,, 9, 9, 90} Mea Media Stadard Deviatio Rage 5. The umber
Name Date Hr. ALGEBRA - SPRING FINAL MULTIPLE CHOICE REVIEW # 5. Which measure of ceter is most appropriate for the followig data set? {7, 7, 75, 77,, 9, 9, 90} Mea Media Stadard Deviatio Rage 5. The umber
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Orientation. Orientation 10/28/15
 Orietatio Orietatio We will defie orietatio to mea a object s istataeous rotatioal cofiguratio Thik of it as the rotatioal equivalet of positio 1 Represetig Positios Cartesia coordiates (x,y,z) are a easy
Orietatio Orietatio We will defie orietatio to mea a object s istataeous rotatioal cofiguratio Thik of it as the rotatioal equivalet of positio 1 Represetig Positios Cartesia coordiates (x,y,z) are a easy
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
The Platonic solids The five regular polyhedra
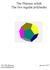 The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Apparent Depth. B' l'
 REFRACTION by PLANE SURFACES Apparet Depth Suppose we have a object B i a medium of idex which is viewed from a medium of idex '. If '
REFRACTION by PLANE SURFACES Apparet Depth Suppose we have a object B i a medium of idex which is viewed from a medium of idex '. If '
Final Exam information
 Fial Exam iformatio Wedesday, Jue 6, 2012, 9:30 am - 11:18 am Locatio: i recitatio room Comprehesive (covers all course material) 35 multiple-choice questios --> 175 poits Closed book ad otes Make up your
Fial Exam iformatio Wedesday, Jue 6, 2012, 9:30 am - 11:18 am Locatio: i recitatio room Comprehesive (covers all course material) 35 multiple-choice questios --> 175 poits Closed book ad otes Make up your
Parametric curves. Reading. Parametric polynomial curves. Mathematical curve representation. Brian Curless CSE 457 Spring 2015
 Readig Required: Agel 0.-0.3, 0.5., 0.6-0.7, 0.9 Parametric curves Bria Curless CSE 457 Sprig 05 Optioal Bartels, Beatty, ad Barsy. A Itroductio to Splies for use i Computer Graphics ad Geometric Modelig,
Readig Required: Agel 0.-0.3, 0.5., 0.6-0.7, 0.9 Parametric curves Bria Curless CSE 457 Sprig 05 Optioal Bartels, Beatty, ad Barsy. A Itroductio to Splies for use i Computer Graphics ad Geometric Modelig,
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
3D Model Retrieval Method Based on Sample Prediction
 20 Iteratioal Coferece o Computer Commuicatio ad Maagemet Proc.of CSIT vol.5 (20) (20) IACSIT Press, Sigapore 3D Model Retrieval Method Based o Sample Predictio Qigche Zhag, Ya Tag* School of Computer
20 Iteratioal Coferece o Computer Commuicatio ad Maagemet Proc.of CSIT vol.5 (20) (20) IACSIT Press, Sigapore 3D Model Retrieval Method Based o Sample Predictio Qigche Zhag, Ya Tag* School of Computer
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
A Resource for Free-standing Mathematics Qualifications
 Ope.ls The first sheet is show elow. It is set up to show graphs with equatios of the form = m + c At preset the values of m ad c are oth zero. You ca chage these values usig the scroll ars. Leave the
Ope.ls The first sheet is show elow. It is set up to show graphs with equatios of the form = m + c At preset the values of m ad c are oth zero. You ca chage these values usig the scroll ars. Leave the
Analysis Metrics. Intro to Algorithm Analysis. Slides. 12. Alg Analysis. 12. Alg Analysis
 Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Size and Shape Parameters
 Defied i the At the momet there is miimal stadardizatio for defiig particle size shape whe usig automated image aalsis. Although particle size distributio calculatios are defied i several stadards (1,
Defied i the At the momet there is miimal stadardizatio for defiig particle size shape whe usig automated image aalsis. Although particle size distributio calculatios are defied i several stadards (1,
Algorithms Chapter 3 Growth of Functions
 Algorithms Chapter 3 Growth of Fuctios Istructor: Chig Chi Li 林清池助理教授 chigchi.li@gmail.com Departmet of Computer Sciece ad Egieerig Natioal Taiwa Ocea Uiversity Outlie Asymptotic otatio Stadard otatios
Algorithms Chapter 3 Growth of Fuctios Istructor: Chig Chi Li 林清池助理教授 chigchi.li@gmail.com Departmet of Computer Sciece ad Egieerig Natioal Taiwa Ocea Uiversity Outlie Asymptotic otatio Stadard otatios
1.8 What Comes Next? What Comes Later?
 35 1.8 What Comes Next? What Comes Later? A Practice Uderstadig Task For each of the followig tables, CC BY Hiroaki Maeda https://flic.kr/p/6r8odk describe how to fid the ext term i the sequece, write
35 1.8 What Comes Next? What Comes Later? A Practice Uderstadig Task For each of the followig tables, CC BY Hiroaki Maeda https://flic.kr/p/6r8odk describe how to fid the ext term i the sequece, write
INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 2 (2013), No. 1, 5-22 INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES NENAD U. STOJANOVIĆ Abstract. If above each side of a regular polygo
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 2 (2013), No. 1, 5-22 INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES NENAD U. STOJANOVIĆ Abstract. If above each side of a regular polygo
Aberrations in Lens & Mirrors (Hecht 6.3)
 Aberratios i Les & Mirrors (Hecht 6.3) Aberratios are failures to focus to a "poit" Both mirrors ad les suffer from these Some are failures of paraxial assumptio 3 5 θ θ si( θ ) = θ + L 3! 5! Paraxial
Aberratios i Les & Mirrors (Hecht 6.3) Aberratios are failures to focus to a "poit" Both mirrors ad les suffer from these Some are failures of paraxial assumptio 3 5 θ θ si( θ ) = θ + L 3! 5! Paraxial
Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 2 4 x 0
 Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Lenses and Imaging (Part I)
 Leses ad Imagig (Part I) Why is imagig ecessary: Huyge s priciple Spherical & parallel ray budles, poits at ifiity efractio at spherical surfaces (paraial approimatio) Optical power ad imagig coditio Matri
Leses ad Imagig (Part I) Why is imagig ecessary: Huyge s priciple Spherical & parallel ray budles, poits at ifiity efractio at spherical surfaces (paraial approimatio) Optical power ad imagig coditio Matri
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Lenses and imaging. MIT 2.71/ /10/01 wk2-a-1
 Leses ad imagig Huyges priciple ad why we eed imagig istrumets A simple imagig istrumet: the pihole camera Priciple of image formatio usig leses Quatifyig leses: paraial approimatio & matri approach Focusig
Leses ad imagig Huyges priciple ad why we eed imagig istrumets A simple imagig istrumet: the pihole camera Priciple of image formatio usig leses Quatifyig leses: paraial approimatio & matri approach Focusig
Our Learning Problem, Again
 Noparametric Desity Estimatio Matthew Stoe CS 520, Sprig 2000 Lecture 6 Our Learig Problem, Agai Use traiig data to estimate ukow probabilities ad probability desity fuctios So far, we have depeded o describig
Noparametric Desity Estimatio Matthew Stoe CS 520, Sprig 2000 Lecture 6 Our Learig Problem, Agai Use traiig data to estimate ukow probabilities ad probability desity fuctios So far, we have depeded o describig
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Lenses and Imaging (Part I) Parabloid mirror: perfect focusing
 Leses ad Imagig (Part I) eview: paraboloid reflector, focusig Why is imagig ecessary: Huyges priciple Spherical & parallel ray budles, poits at ifiity efractio at spherical surfaces (paraial approimatio)
Leses ad Imagig (Part I) eview: paraboloid reflector, focusig Why is imagig ecessary: Huyges priciple Spherical & parallel ray budles, poits at ifiity efractio at spherical surfaces (paraial approimatio)
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
Algorithm. Counting Sort Analysis of Algorithms
 Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
APPLICATION NOTE PACE1750AE BUILT-IN FUNCTIONS
 APPLICATION NOTE PACE175AE BUILT-IN UNCTIONS About This Note This applicatio brief is iteded to explai ad demostrate the use of the special fuctios that are built ito the PACE175AE processor. These powerful
APPLICATION NOTE PACE175AE BUILT-IN UNCTIONS About This Note This applicatio brief is iteded to explai ad demostrate the use of the special fuctios that are built ito the PACE175AE processor. These powerful
