CS 267 Sources of. Parallelism and Locality in Simulation. Lecture 4" James Demmel!
|
|
|
- Elvin Shelton
- 5 years ago
- Views:
Transcription
1 Parallelism and Locality in Simulation CS 267 Sources of Parallelism and Locality in Simulation Lecture 4" James Demmel! Parallelism and data locality both critical to performance Recall that moving data is the most expensive operation Real world problems have parallelism and locality: Many objects operate independently of others. Objects often depend much more on nearby than distant objects. Dependence on distant objects can often be simplified. Example of all three: particles moving under gravity Scientific models may introduce more parallelism: When a continuous problem is discretized, time dependencies are generally limited to adjacent time steps. Helps limit dependence to nearby objects (eg collisions) Far-field effects may be ignored or approximated in many cases. Many problems exhibit parallelism at multiple levels CS267 Lecture 4! 1! 01/30/2014! CS267 Lecture 4! 2! Basic Kinds of Simulation Discrete event systems: Game of Life, Manufacturing systems, Finance, Circuits, Pacman, Particle systems: Billiard balls, Galaxies, Atoms, Circuits, Pinball Lumped variables depending on continuous parameters aka Ordinary Differential Equations (ODEs), Structural mechanics, Chemical kinetics, Circuits, Star Wars: The Force Unleashed Continuous variables depending on continuous parameters aka Partial Differential Equations (PDEs) Heat, Elasticity, Electrostatics, Finance, Circuits, Medical Image Analysis, Terminator 3: Rise of the Machines A given phenomenon can be modeled at multiple levels. Many simulations combine more than one of these techniques. For more on simulation in games, see 01/30/2014! CS267 Lecture 4! 3! Example: Circuit Simulation Circuits are simulated at many different levels Discrete Event Lumped Systems Continuous Systems Level Primitives Examples Instruction level Instructions SimOS, SPIM Cycle level Functional units VIRAM-p Register Transfer Level (RTL) Gate Level Register, counter, MUX Gate, flip-flop, memory cell VHDL Switch level Ideal transistor Cosmos Circuit level Device level Resistors, capacitors, etc. Electrons, silicon Spice Thor 01/30/2014! CS267 Lecture 4! 4! CS267 Lecture 2 1
2 Outline Discrete event systems Time and space are discrete Particle systems Important special case of lumped systems Lumped systems (ODEs) Location/entities are discrete, time is continuous Continuous systems (PDEs) Time and space are continuous Next lecture Identify common problems and solutions discrete continuous A Model Problem: Sharks and Fish Illustration of parallel programming Original version (discrete event only) proposed by Geoffrey Fox Called WATOR Basic idea: sharks and fish living in an ocean rules for movement (discrete and continuous) breeding, eating, and death forces in the ocean forces between sea creatures 6 problems (S&F1 - S&F6) Different sets of rules, to illustrate different phenomena Available in many languages (see class web page) Matlab, pthreads, MPI, OpenMP, Split-C, Titanium, CMF, CMMD, psather (not all problems in all languages) Some homework based on these 01/30/2014! CS267 Lecture 4! 5! 01/30/2014! CS267 Lecture 4! 6! Sharks and Fish S&F 1. Fish alone move continuously subject to an external current and Newton's laws. S&F 2. Fish alone move continuously subject to gravitational attraction and Newton's laws. S&F 3. Fish alone play the "Game of Life" on a square grid. S&F 4. Fish alone move randomly on a square grid, with at most one fish per grid point. S&F 5. Sharks and Fish both move randomly on a square grid, with at most one fish or shark per grid point, including rules for fish attracting sharks, eating, breeding and dying. S&F 6. Like Sharks and Fish 5, but continuous, subject to Newton's laws. 01/30/2014! CS267 Lecture 4! 7! Discrete Event Systems" CS267 Lecture 4! 8! CS267 Lecture 2 2
3 Discrete Event Systems Systems are represented as: finite set of variables. the set of all variable values at a given time is called the state. each variable is updated by computing a transition function depending on the other variables. System may be: synchronous: at each discrete timestep evaluate all transition functions; also called a state machine. asynchronous: transition functions are evaluated only if the inputs change, based on an event from another part of the system; also called event driven simulation. Example: The game of life: Also known as Sharks and Fish #3: Space divided into cells, rules govern cell contents at each step Parallelism in Game of Life (S&F 3) The simulation is synchronous use two copies of the grid (old and new), ping-pong between them the value of each new grid cell depends only on 9 cells (itself plus 8 neighbors) in old grid. simulation proceeds in timesteps-- each cell is updated at every step. Easy to parallelize by dividing physical domain: Domain Decomposition P1 P2 P3 P4 P5 P6 P7 P8 P9 Repeat compute locally to update local system barrier() exchange state info with neighbors finish updates until done simulating Locality is achieved by using large patches of the ocean Only boundary values from neighboring patches are needed. How to pick shapes of domains? 01/30/2014! CS267 Lecture 4! 9! 01/30/2014! CS267 Lecture 4! 10! Regular Meshes (e.g. Game of Life) Suppose graph is nxn mesh with connection NSEW neighbors Which partition has less communication? (n=18, p=9) Minimizing communication on mesh minimizing surface to volume ratio of partition n*(p-1) edge crossings 2*n*(p 1/2 1) edge crossings Synchronous Circuit Simulation Circuit is a graph made up of subcircuits connected by wires Component simulations need to interact if they share a wire. Data structure is (irregular) graph of subcircuits. Parallel algorithm is timing-driven or synchronous: Evaluate all components at every timestep (determined by known circuit delay) Graph partitioning assigns subgraphs to processors Determines parallelism and locality. Goal 1 is to evenly distribute subgraphs to nodes (load balance). Goal 2 is to minimize edge crossings (minimize communication). Easy for meshes, NP-hard in general, so we will approximate (future lecture) better 01/30/2014! CS267 Lecture 4! 11! edge crossings = 6 edge crossings = 10 01/30/2014! CS267 Lecture 4! 12! CS267 Lecture 2 3
4 Sharks & Fish in Loosely Connected Ponds Parallelization: each processor gets a set of ponds with roughly equal total area work is proportional to area, not number of creatures One pond can affect another (through streams) but infrequently 01/30/2014! CS267 Lecture 4! 13! Asynchronous Simulation Synchronous simulations may waste time: Simulates even when the inputs do not change Asynchronous (event-driven) simulations update only when an event arrives from another component: No global time steps, but individual events contain time stamp. Example: Game of life in loosely connected ponds (don t simulate empty ponds). Example: Circuit simulation with delays (events are gates changing). Example: Traffic simulation (events are cars changing lanes, etc.). Asynchronous is more efficient, but harder to parallelize In MPI, events are naturally implemented as messages, but how do you know when to execute a receive? 01/30/2014! CS267 Lecture 4! 14! Scheduling Asynchronous Circuit Simulation Conservative: Only simulate up to (and including) the minimum time stamp of inputs. Need deadlock detection if there are cycles in graph Example on next slide Example: Pthor circuit simulator in Splash1 from Stanford. Speculative (or Optimistic): Assume no new inputs will arrive and keep simulating. May need to backup if assumption wrong, using timestamps Example: Timewarp [D. Jefferson], Parswec [Wen,Yelick]. Optimizing load balance and locality is difficult: Locality means putting tightly coupled subcircuit on one processor. Since active part of circuit likely to be in a tightly coupled subcircuit, this may be bad for load balance. 01/30/2014! CS267 Lecture 4! 15! Deadlock in Conservative Asynchronous Circuit Simulation Example: Sharks & Fish 3, with 3 processors simulating 3 ponds connected by streams along which fish can move Suppose all ponds simulated up to time t 0, but no fish move, so no messages sent from one proc to another So no processor can simulate past time t 0 Fix: After waiting for an incoming message for a while, send out an Are you stuck too? message If you ever receive such a message, pass it on If you receive such a message that you sent, you have a deadlock cycle, so just take a step with latest input Can be a serial bottleneck 01/30/2014! CS267 Lecture 4! 16! CS267 Lecture 2 4
5 Summary of Discrete Event Simulations Model of the world is discrete Both time and space Approaches Decompose domain, i.e., set of objects Run each component ahead using Synchronous: communicate at end of each timestep Asynchronous: communicate on-demand Conservative scheduling wait for inputs need deadlock detection Speculative scheduling assume no inputs roll back if necessary 01/30/2014! CS267 Lecture 4! 17! Summary of Lecture so far Parallelism and Locality arise naturally in simulation So far: Discrete Event Simulation (time and space discrete) Next: Particle Systems, Lumped variables (ODEs), Continuous variables (PDEs) Discrete Event Simulation Game of Life, Digital Circuits, Pacman, Finite set of variables, values at a given time called state Each variable updated by transition function depending on others Synchronous: update all values at each discrete timestep Asynchronous: update a value only if inputs change, when an event occurs; also called event driven simulation 01/30/2014! CS267 Lecture 4! 18! Particle Systems Particle Systems" CS267 Lecture 4! 19! A particle system has a finite number of particles moving in space according to Newton s Laws (i.e. F = ma) time is continuous Examples stars in space with laws of gravity electron beam in semiconductor manufacturing atoms in a molecule with electrostatic forces neutrons in a fission reactor cars on a freeway with Newton s laws plus model of driver and engine balls in a pinball game Reminder: many simulations combine techniques such as particle simulations with some discrete events (Ex Sharks and Fish) 01/30/2014! CS267 Lecture 4! 20! CS267 Lecture 2 5
6 Forces in Particle Systems Force on each particle can be subdivided force = external_force + nearby_force + far_field_force External force ocean current in sharks and fish world (S&F 1) externally imposed electric field in electron beam Nearby force sharks attracted to eat nearby fish (S&F 5) balls on a billiard table bounce off of each other Van der Waals forces in fluid (1/r^6) how Gecko feet work? Far-field force fish attract other fish by gravity-like (1/r^2 ) force (S&F 2) gravity, electrostatics, radiosity in graphics forces governed by elliptic PDE Example S&F 1: Fish in an External Current % fishp = array of initial fish positions (stored as complex numbers) % fishv = array of initial fish velocities (stored as complex numbers) % fishm = array of masses of fish % tfinal = final time for simulation (0 = initial time) % Algorithm: integrate using Euler's method with varying step size % Initialize time step, iteration count, and array of times dt =.01; t = 0; % loop over time steps while t < tfinal, t = t + dt; fishp = fishp + dt*fishv; accel = current(fishp)./fishm; % current depends on position fishv = fishv + dt*accel; % update time step (small enough to be accurate, but not too small) dt = min(.1*max(abs(fishv))/max(abs(accel)),1); end 01/30/2014! CS267 Lecture 4! 21! 01/30/2014! CS267 Lecture 4! 22! Parallelism in External Forces These are the simplest The force on each particle is independent Called embarrassingly parallel Sometimes called map reduce by analogy Evenly distribute particles on processors Any distribution works Locality is not an issue, no communication For each particle on processor, apply the external force Also called map May need to reduce (eg compute maximum) to compute time step, other data Parallelism in Nearby Forces Nearby forces require interaction and therefore communication. Force may depend on other nearby particles: Example: collisions. simplest algorithm is O(n 2 ): look at all pairs to see if they collide. Usual parallel model is domain decomposition of physical region in which particles are located O(n/p) particles per processor if evenly distributed. 01/30/2014! CS267 Lecture 4! 23! 01/30/2014! CS267 Lecture 4! 24! CS267 Lecture 2 6
7 Parallelism in Nearby Forces Challenge 1: interactions of particles near processor boundary: need to communicate particles near boundary to neighboring processors. Region near boundary called ghost zone Low surface to volume ratio means low communication. Use squares, not slabs, to minimize ghost zone sizes Parallelism in Nearby Forces Challenge 2: load imbalance, if particles cluster: galaxies, electrons hitting a device wall. To reduce load imbalance, divide space unevenly. Each region contains roughly equal number of particles. Quad-tree in 2D, oct-tree in 3D. Communicate particles in boundary region to neighbors! Example: each square contains at most 3 particles! Need to check for collisions between regions! 01/30/2014! CS267 Lecture 4! 25! 01/30/2014! CS267 Lecture 4! 26! Parallelism in Far-Field Forces Far-field forces involve all-to-all interaction and therefore communication. Force depends on all other particles: Examples: gravity, protein folding Simplest algorithm is O(n 2 ) as in S&F 2, 4, 5. Just decomposing space does not help since every particle needs to visit every other particle. Implement by rotating particle sets. Keeps processors busy All processors eventually see all particles Use more clever algorithms to reduce communication Use more clever algorithms to beat O(n 2 ). 01/30/2014! CS267 Lecture 4! 27! Far-field Forces: Particle-Mesh Methods Based on approximation: Superimpose a regular mesh. Move particles to nearest grid point. Exploit fact that the far-field force satisfies a PDE that is easy to solve on a regular mesh: FFT, multigrid (described in future lectures) Cost drops to O(n log n) or O(n) instead of O(n 2 ) Accuracy depends on the fineness of the grid is and the uniformity of the particle distribution. 1) Particles are moved to nearby mesh points (scatter) 2) Solve mesh problem 3) Forces are interpolated at particles from mesh points (gather) 01/30/2014! CS267 Lecture 4! 28! CS267 Lecture 2 7
8 Far-field forces: Tree Decomposition Based on approximation. Forces from group of far-away particles simplified -- resembles a single large particle. Use tree; each node contains an approximation of descendants. Also O(n log n) or O(n) instead of O(n 2 ). Several Algorithms Barnes-Hut. Fast multipole method (FMM) of Greengard/Rohklin. Anderson s method. Summary of Particle Methods Model contains discrete entities, namely, particles Time is continuous must be discretized to solve Simulation follows particles through timesteps Force = external _force + nearby_force + far_field_force All-pairs algorithm is simple, but inefficient, O(n 2 ) Particle-mesh methods approximates by moving particles to a regular mesh, where it is easier to compute forces Tree-based algorithms approximate by treating set of particles as a group, when far away Discussed in later lecture. May think of this as a special case of a lumped system 01/30/2014! CS267 Lecture 4! 29! 01/30/2014! CS267 Lecture 4! 30! Lumped Systems: ODEs" System of Lumped Variables Many systems are approximated by System of lumped variables. Each depends on continuous parameter (usually time). Example -- circuit: approximate as graph. wires are edges. nodes are connections between 2 or more wires. each edge has resistor, capacitor, inductor or voltage source. system is lumped because we are not computing the voltage/ current at every point in space along a wire, just endpoints. Variables related by Ohm s Law, Kirchoff s Laws, etc. Forms a system of ordinary differential equations (ODEs). Differentiated with respect to time Variant: ODEs with some constraints Also called DAEs, Differential Algebraic Equations CS267 Lecture 4! 31! 01/30/2014! CS267 Lecture 4! 32! CS267 Lecture 2 8
9 Circuit Example State of the system is represented by v n (t) node voltages i b (t) branch currents all at time t v b (t) branch voltages Equations include Kirchoff s current Kirchoff s voltage Ohm s law Capacitance Inductance 0 A 0 v n 0 A 0 -I * i b = S 0 R -I v b 0 0 -I C*d/dt 0 0 L*d/dt I 0 Structural Analysis Example Another example is structural analysis in civil engineering: Variables are displacement of points in a building. Newton s and Hook s (spring) laws apply. Static modeling: exert force and determine displacement. Dynamic modeling: apply continuous force (earthquake). Eigenvalue problem: do the resonant modes of the building match an earthquake A is sparse matrix, representing connections in circuit One column per branch (edge), one row per node (vertex) with +1 and -1 in each column at rows indicating end points Write as single large system of ODEs or DAEs 01/30/2014! CS267 Lecture 4! 33! OpenSees project in CE at Berkeley looks at this section of 880, among others 01/30/2014! CS267 Lecture 4! 34! Gaming Example Star Wars The Force Unleashed Solving ODEs In these examples, and most others, the matrices are sparse: i.e., most array elements are 0. neither store nor compute on these 0 s. Sparse because each component only depends on a few others Given a set of ODEs, two kinds of questions are: Compute the values of the variables at some time t Explicit methods Implicit methods Compute modes of vibration Eigenvalue problems 01/30/2014! CS267 Lecture 4! 35! 01/30/2014! CS267 Lecture 4! 36! CS267 Lecture 2 9
10 Solving ODEs: Explicit Methods Assume ODE is x (t) = f(x) = A*x(t), where A is a sparse matrix Compute x(i*dt) = x[i] at i=0,1,2, ODE gives x (i*dt) = slope x[i+1]=x[i] + dt*slope Use slope at x[i] Explicit methods, e.g., (Forward) Euler s method. Approximate x (t)=a*x(t) by (x[i+1] - x[i] )/dt = A*x[i]. x[i+1] = x[i]+dt*a*x[i], i.e. sparse matrix-vector multiplication. Tradeoffs: Simple algorithm: sparse matrix vector multiply. Stability problems: May need to take very small time steps, especially if system is stiff (i.e. A has some large entries, so x can change rapidly). 01/30/2014! CS267 Lecture 4! 37! t (i) t+dt (i+1) Solving ODEs: Implicit Methods Assume ODE is x (t) = f(x) = A*x(t), where A is a sparse matrix Compute x(i*dt) = x[i] at i=0,1,2, ODE gives x ((i+1)*dt) = slope x[i+1]=x[i] + dt*slope Use slope at x[i+1] t (i) t t t+dt + (i+1) Implicit method, e.g., Backward Euler solve: Approximate x (t)=a*x(t) by (x[i+1] - x[i] )/dt = A*x[i+1]. (I - dt*a)*x[i+1] = x[i], i.e. we need to solve a sparse linear system of equations. Trade-offs: Larger timestep possible: especially for stiff problems More difficult algorithm: need to solve a sparse linear system of equations at each step 01/30/2014! CS267 Lecture 4! 38! Solving ODEs: Eigensolvers Computing modes of vibration: finding eigenvalues and eigenvectors. Seek solution of d 2 x(t)/dt 2 = A*x(t) of form x(t) = sin(ω*t) * x 0, where x 0 is a constant vector ω called the frequency of vibration x 0 sometimes called a mode shape Plug in to get -ω 2 *x 0 = A*x 0, so that ω 2 is an eigenvalue and x 0 is an eigenvector of A. Solution schemes reduce either to sparse-matrix multiplication, or solving sparse linear systems. Implicit Methods; Eigenproblems Implicit methods for ODEs need to solve linear systems Direct methods (Gaussian elimination) Called LU Decomposition, because we factor A = L*U. Future lectures will consider both dense and sparse cases. More complicated than sparse-matrix vector multiplication. Iterative solvers Will discuss several of these in future. Jacobi, Successive over-relaxation (SOR), Conjugate Gradient (CG), Multigrid,... Most have sparse-matrix-vector multiplication in kernel. Eigenproblems Future lectures will discuss dense and sparse cases. Also depend on sparse-matrix-vector multiplication, direct methods. 01/30/2014! CS267 Lecture 4! 39! 01/30/2014! CS267 Lecture 4! 40! CS267 Lecture 2 10
11 ODEs and Sparse Matrices All these problems reduce to sparse matrix problems Explicit: sparse matrix-vector multiplication (SpMV). Implicit: solve a sparse linear system direct solvers (Gaussian elimination). iterative solvers (use sparse matrix-vector multiplication). Eigenvalue/vector algorithms may also be explicit or implicit. Conclusion: SpMV is key to many ODE problems Relatively simple algorithm to study in detail Two key problems: locality and load balance 01/30/2014! CS267 Lecture 4! 41! y SpMV in Compressed Sparse Row (CSR) Format SpMV: y = y + A*x, only store, do arithmetic, on nonzero entries CSR format is simplest one of many possible data structures for A x Representation of A A Matrix-vector multiply kernel: y(i) ß y(i) + A(i,j) x(j) for each row i for k=ptr[i] to ptr[i+1]-1 do y[i] = y[i] + val[k]*x[ind[k]] 01/30/2014! CS267 Lecture 4! 42! Parallel Sparse Matrix-vector multiplication y = A*x, where A is a sparse n x n matrix Questions which processors store y[i], x[i], and A[i,j] which processors compute y P2 P3 P4 y[i] = sum (from 1 to n) A[i,j] * x[j] = (row i of A) * x a sparse dot product Partitioning Partition index set {1,,n} = N1 N2 Np. May require communication For all i in Nk, Processor k stores y[i], x[i], and row i of A For all i in Nk, Processor k computes y[i] = (row i of A) * x owner computes rule: Processor k compute the y[i]s it owns. 01/30/2014! CS267 Lecture 4! 43! x P1 Matrix Reordering via Graph Partitioning Ideal matrix structure for parallelism: block diagonal p (number of processors) blocks, can all be computed locally. If no non-zeros outside these blocks, no communication needed Can we reorder the rows/columns to get close to this? Most nonzeros in diagonal blocks, few outside P0 P1 P2 P3 P4! = * P0! P1! P2! P3! P4! 01/30/2014! CS267 Lecture 4! 44! CS267 Lecture 2 11
12 Goals of Reordering Performance goals balance load (how is load measured?). Approx equal number of nonzeros (not necessarily rows) balance storage (how much does each processor store?). Approx equal number of nonzeros minimize communication (how much is communicated?). Minimize nonzeros outside diagonal blocks Related optimization criterion is to move nonzeros near diagonal improve register and cache re-use Group nonzeros in small vertical blocks so source (x) elements loaded into cache or registers may be reused (temporal locality) Group nonzeros in small horizontal blocks so nearby source (x) elements in the cache may be used (spatial locality) Other algorithms reorder for other reasons Reduce # nonzeros in matrix after Gaussian elimination Improve numerical stability 01/30/2014! CS267 Lecture 4! 45! Graph Partitioning and Sparse Matrices Relationship between matrix and graph Edges in the graph are nonzero in the matrix: here the matrix is symmetric (edges are unordered) and weights are equal (1) If divided over 3 procs, there are 14 nonzeros outside the diagonal blocks, which represent the 7 (bidirectional) edges 01/30/2014! CS267 Lecture 4! 46! Summary: Common Problems Load Balancing Dynamically if load changes significantly during job Statically - Graph partitioning Discrete systems Sparse matrix vector multiplication Linear algebra Solving linear systems (sparse and dense) Eigenvalue problems will use similar techniques Fast Particle Methods O(n log n) instead of O(n 2 ) 01/30/2014! CS267 Lecture 4! 47! What do commercial and CSE applications have in common? Motif/Dwarf: Common Computational Methods (Red Hot Blue Cool) 1 Finite State Mach. 2 Combinational 3 Graph Traversal 4 Structured Grid 5 Dense Matrix 6 Sparse Matrix 7 Spectral (FFT) 8 Dynamic Prog 9 N-Body 10 MapReduce 11 Backtrack/ B&B 12 Graphical Models 13 Unstructured Grid 01/30/2014! Embed SPEC DB Games ML HPC Health Image Speech Music Browser CS267 Lecture 4! 48! CS267 Lecture 2 12
Lecture 4: Locality and parallelism in simulation I
 Lecture 4: Locality and parallelism in simulation I David Bindel 6 Sep 2011 Logistics Distributed memory machines Each node has local memory... and no direct access to memory on other nodes Nodes communicate
Lecture 4: Locality and parallelism in simulation I David Bindel 6 Sep 2011 Logistics Distributed memory machines Each node has local memory... and no direct access to memory on other nodes Nodes communicate
Lecture 15: More Iterative Ideas
 Lecture 15: More Iterative Ideas David Bindel 15 Mar 2010 Logistics HW 2 due! Some notes on HW 2. Where we are / where we re going More iterative ideas. Intro to HW 3. More HW 2 notes See solution code!
Lecture 15: More Iterative Ideas David Bindel 15 Mar 2010 Logistics HW 2 due! Some notes on HW 2. Where we are / where we re going More iterative ideas. Intro to HW 3. More HW 2 notes See solution code!
AMS526: Numerical Analysis I (Numerical Linear Algebra)
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 20: Sparse Linear Systems; Direct Methods vs. Iterative Methods Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 26
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 20: Sparse Linear Systems; Direct Methods vs. Iterative Methods Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 26
Shared Memory Programming. Parallel Programming Overview
 Shared Memory Programming Arvind Krishnamurthy Fall 2004 Parallel Programming Overview Basic parallel programming problems: 1. Creating parallelism & managing parallelism Scheduling to guarantee parallelism
Shared Memory Programming Arvind Krishnamurthy Fall 2004 Parallel Programming Overview Basic parallel programming problems: 1. Creating parallelism & managing parallelism Scheduling to guarantee parallelism
Roofline Model (Will be using this in HW2)
 Parallel Architecture Announcements HW0 is due Friday night, thank you for those who have already submitted HW1 is due Wednesday night Today Computing operational intensity Dwarves and Motifs Stencil computation
Parallel Architecture Announcements HW0 is due Friday night, thank you for those who have already submitted HW1 is due Wednesday night Today Computing operational intensity Dwarves and Motifs Stencil computation
HPC Algorithms and Applications
 HPC Algorithms and Applications Dwarf #5 Structured Grids Michael Bader Winter 2012/2013 Dwarf #5 Structured Grids, Winter 2012/2013 1 Dwarf #5 Structured Grids 1. dense linear algebra 2. sparse linear
HPC Algorithms and Applications Dwarf #5 Structured Grids Michael Bader Winter 2012/2013 Dwarf #5 Structured Grids, Winter 2012/2013 1 Dwarf #5 Structured Grids 1. dense linear algebra 2. sparse linear
Adaptive-Mesh-Refinement Pattern
 Adaptive-Mesh-Refinement Pattern I. Problem Data-parallelism is exposed on a geometric mesh structure (either irregular or regular), where each point iteratively communicates with nearby neighboring points
Adaptive-Mesh-Refinement Pattern I. Problem Data-parallelism is exposed on a geometric mesh structure (either irregular or regular), where each point iteratively communicates with nearby neighboring points
Principles of Parallel Algorithm Design: Concurrency and Mapping
 Principles of Parallel Algorithm Design: Concurrency and Mapping John Mellor-Crummey Department of Computer Science Rice University johnmc@rice.edu COMP 422/534 Lecture 3 17 January 2017 Last Thursday
Principles of Parallel Algorithm Design: Concurrency and Mapping John Mellor-Crummey Department of Computer Science Rice University johnmc@rice.edu COMP 422/534 Lecture 3 17 January 2017 Last Thursday
Contents. F10: Parallel Sparse Matrix Computations. Parallel algorithms for sparse systems Ax = b. Discretized domain a metal sheet
 Contents 2 F10: Parallel Sparse Matrix Computations Figures mainly from Kumar et. al. Introduction to Parallel Computing, 1st ed Chap. 11 Bo Kågström et al (RG, EE, MR) 2011-05-10 Sparse matrices and storage
Contents 2 F10: Parallel Sparse Matrix Computations Figures mainly from Kumar et. al. Introduction to Parallel Computing, 1st ed Chap. 11 Bo Kågström et al (RG, EE, MR) 2011-05-10 Sparse matrices and storage
2.7 Cloth Animation. Jacobs University Visualization and Computer Graphics Lab : Advanced Graphics - Chapter 2 123
 2.7 Cloth Animation 320491: Advanced Graphics - Chapter 2 123 Example: Cloth draping Image Michael Kass 320491: Advanced Graphics - Chapter 2 124 Cloth using mass-spring model Network of masses and springs
2.7 Cloth Animation 320491: Advanced Graphics - Chapter 2 123 Example: Cloth draping Image Michael Kass 320491: Advanced Graphics - Chapter 2 124 Cloth using mass-spring model Network of masses and springs
CS 267 Applications of Parallel Computers. Lecture 23: Load Balancing and Scheduling. James Demmel
 CS 267 Applications of Parallel Computers Lecture 23: Load Balancing and Scheduling James Demmel http://www.cs.berkeley.edu/~demmel/cs267_spr99 CS267 L23 Load Balancing and Scheduling.1 Demmel Sp 1999
CS 267 Applications of Parallel Computers Lecture 23: Load Balancing and Scheduling James Demmel http://www.cs.berkeley.edu/~demmel/cs267_spr99 CS267 L23 Load Balancing and Scheduling.1 Demmel Sp 1999
Multigrid Pattern. I. Problem. II. Driving Forces. III. Solution
 Multigrid Pattern I. Problem Problem domain is decomposed into a set of geometric grids, where each element participates in a local computation followed by data exchanges with adjacent neighbors. The grids
Multigrid Pattern I. Problem Problem domain is decomposed into a set of geometric grids, where each element participates in a local computation followed by data exchanges with adjacent neighbors. The grids
The Jello Cube Assignment 1, CSCI 520. Jernej Barbic, USC
 The Jello Cube Assignment 1, CSCI 520 Jernej Barbic, USC 1 The jello cube Undeformed cube Deformed cube The jello cube is elastic, Can be bent, stretched, squeezed,, Without external forces, it eventually
The Jello Cube Assignment 1, CSCI 520 Jernej Barbic, USC 1 The jello cube Undeformed cube Deformed cube The jello cube is elastic, Can be bent, stretched, squeezed,, Without external forces, it eventually
Simulation in Computer Graphics. Deformable Objects. Matthias Teschner. Computer Science Department University of Freiburg
 Simulation in Computer Graphics Deformable Objects Matthias Teschner Computer Science Department University of Freiburg Outline introduction forces performance collision handling visualization University
Simulation in Computer Graphics Deformable Objects Matthias Teschner Computer Science Department University of Freiburg Outline introduction forces performance collision handling visualization University
Solving Sparse Linear Systems. Forward and backward substitution for solving lower or upper triangular systems
 AMSC 6 /CMSC 76 Advanced Linear Numerical Analysis Fall 7 Direct Solution of Sparse Linear Systems and Eigenproblems Dianne P. O Leary c 7 Solving Sparse Linear Systems Assumed background: Gauss elimination
AMSC 6 /CMSC 76 Advanced Linear Numerical Analysis Fall 7 Direct Solution of Sparse Linear Systems and Eigenproblems Dianne P. O Leary c 7 Solving Sparse Linear Systems Assumed background: Gauss elimination
L17: Introduction to Irregular Algorithms and MPI, cont.! November 8, 2011!
 L17: Introduction to Irregular Algorithms and MPI, cont.! November 8, 2011! Administrative Class cancelled, Tuesday, November 15 Guest Lecture, Thursday, November 17, Ganesh Gopalakrishnan CUDA Project
L17: Introduction to Irregular Algorithms and MPI, cont.! November 8, 2011! Administrative Class cancelled, Tuesday, November 15 Guest Lecture, Thursday, November 17, Ganesh Gopalakrishnan CUDA Project
EFFICIENT SOLVER FOR LINEAR ALGEBRAIC EQUATIONS ON PARALLEL ARCHITECTURE USING MPI
 EFFICIENT SOLVER FOR LINEAR ALGEBRAIC EQUATIONS ON PARALLEL ARCHITECTURE USING MPI 1 Akshay N. Panajwar, 2 Prof.M.A.Shah Department of Computer Science and Engineering, Walchand College of Engineering,
EFFICIENT SOLVER FOR LINEAR ALGEBRAIC EQUATIONS ON PARALLEL ARCHITECTURE USING MPI 1 Akshay N. Panajwar, 2 Prof.M.A.Shah Department of Computer Science and Engineering, Walchand College of Engineering,
The jello cube. Undeformed cube. Deformed cube
 The Jello Cube Assignment 1, CSCI 520 Jernej Barbic, USC Undeformed cube The jello cube Deformed cube The jello cube is elastic, Can be bent, stretched, squeezed,, Without external forces, it eventually
The Jello Cube Assignment 1, CSCI 520 Jernej Barbic, USC Undeformed cube The jello cube Deformed cube The jello cube is elastic, Can be bent, stretched, squeezed,, Without external forces, it eventually
Principles of Parallel Algorithm Design: Concurrency and Mapping
 Principles of Parallel Algorithm Design: Concurrency and Mapping John Mellor-Crummey Department of Computer Science Rice University johnmc@rice.edu COMP 422/534 Lecture 3 28 August 2018 Last Thursday Introduction
Principles of Parallel Algorithm Design: Concurrency and Mapping John Mellor-Crummey Department of Computer Science Rice University johnmc@rice.edu COMP 422/534 Lecture 3 28 August 2018 Last Thursday Introduction
PHYSICALLY BASED ANIMATION
 PHYSICALLY BASED ANIMATION CS148 Introduction to Computer Graphics and Imaging David Hyde August 2 nd, 2016 WHAT IS PHYSICS? the study of everything? WHAT IS COMPUTATION? the study of everything? OUTLINE
PHYSICALLY BASED ANIMATION CS148 Introduction to Computer Graphics and Imaging David Hyde August 2 nd, 2016 WHAT IS PHYSICS? the study of everything? WHAT IS COMPUTATION? the study of everything? OUTLINE
CMSC 714 Lecture 6 MPI vs. OpenMP and OpenACC. Guest Lecturer: Sukhyun Song (original slides by Alan Sussman)
 CMSC 714 Lecture 6 MPI vs. OpenMP and OpenACC Guest Lecturer: Sukhyun Song (original slides by Alan Sussman) Parallel Programming with Message Passing and Directives 2 MPI + OpenMP Some applications can
CMSC 714 Lecture 6 MPI vs. OpenMP and OpenACC Guest Lecturer: Sukhyun Song (original slides by Alan Sussman) Parallel Programming with Message Passing and Directives 2 MPI + OpenMP Some applications can
CS 140: Sparse Matrix-Vector Multiplication and Graph Partitioning
 CS 140: Sparse Matrix-Vector Multiplication and Graph Partitioning Parallel sparse matrix-vector product Lay out matrix and vectors by rows y(i) = sum(a(i,j)*x(j)) Only compute terms with A(i,j) 0 P0 P1
CS 140: Sparse Matrix-Vector Multiplication and Graph Partitioning Parallel sparse matrix-vector product Lay out matrix and vectors by rows y(i) = sum(a(i,j)*x(j)) Only compute terms with A(i,j) 0 P0 P1
Multigrid James Demmel
 Multigrid James Demmel www.cs.berkeley.edu/~demmel/ma221 Review of Previous Lectures and Outline Review Poisson equation Overview of Methods for Poisson Equation Jacobi s method Gauss-Seidel method Red-Black
Multigrid James Demmel www.cs.berkeley.edu/~demmel/ma221 Review of Previous Lectures and Outline Review Poisson equation Overview of Methods for Poisson Equation Jacobi s method Gauss-Seidel method Red-Black
Parallel Implementations of Gaussian Elimination
 s of Western Michigan University vasilije.perovic@wmich.edu January 27, 2012 CS 6260: in Parallel Linear systems of equations General form of a linear system of equations is given by a 11 x 1 + + a 1n
s of Western Michigan University vasilije.perovic@wmich.edu January 27, 2012 CS 6260: in Parallel Linear systems of equations General form of a linear system of equations is given by a 11 x 1 + + a 1n
Summer 2009 REU: Introduction to Some Advanced Topics in Computational Mathematics
 Summer 2009 REU: Introduction to Some Advanced Topics in Computational Mathematics Moysey Brio & Paul Dostert July 4, 2009 1 / 18 Sparse Matrices In many areas of applied mathematics and modeling, one
Summer 2009 REU: Introduction to Some Advanced Topics in Computational Mathematics Moysey Brio & Paul Dostert July 4, 2009 1 / 18 Sparse Matrices In many areas of applied mathematics and modeling, one
Homework # 2 Due: October 6. Programming Multiprocessors: Parallelism, Communication, and Synchronization
 ECE669: Parallel Computer Architecture Fall 2 Handout #2 Homework # 2 Due: October 6 Programming Multiprocessors: Parallelism, Communication, and Synchronization 1 Introduction When developing multiprocessor
ECE669: Parallel Computer Architecture Fall 2 Handout #2 Homework # 2 Due: October 6 Programming Multiprocessors: Parallelism, Communication, and Synchronization 1 Introduction When developing multiprocessor
High Performance Computing: Tools and Applications
 High Performance Computing: Tools and Applications Edmond Chow School of Computational Science and Engineering Georgia Institute of Technology Lecture 15 Numerically solve a 2D boundary value problem Example:
High Performance Computing: Tools and Applications Edmond Chow School of Computational Science and Engineering Georgia Institute of Technology Lecture 15 Numerically solve a 2D boundary value problem Example:
Homework # 1 Due: Feb 23. Multicore Programming: An Introduction
 C O N D I T I O N S C O N D I T I O N S Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.86: Parallel Computing Spring 21, Agarwal Handout #5 Homework #
C O N D I T I O N S C O N D I T I O N S Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.86: Parallel Computing Spring 21, Agarwal Handout #5 Homework #
Why Use the GPU? How to Exploit? New Hardware Features. Sparse Matrix Solvers on the GPU: Conjugate Gradients and Multigrid. Semiconductor trends
 Imagine stream processor; Bill Dally, Stanford Connection Machine CM; Thinking Machines Sparse Matrix Solvers on the GPU: Conjugate Gradients and Multigrid Jeffrey Bolz Eitan Grinspun Caltech Ian Farmer
Imagine stream processor; Bill Dally, Stanford Connection Machine CM; Thinking Machines Sparse Matrix Solvers on the GPU: Conjugate Gradients and Multigrid Jeffrey Bolz Eitan Grinspun Caltech Ian Farmer
Cloth Simulation. COMP 768 Presentation Zhen Wei
 Cloth Simulation COMP 768 Presentation Zhen Wei Outline Motivation and Application Cloth Simulation Methods Physically-based Cloth Simulation Overview Development References 2 Motivation Movies Games VR
Cloth Simulation COMP 768 Presentation Zhen Wei Outline Motivation and Application Cloth Simulation Methods Physically-based Cloth Simulation Overview Development References 2 Motivation Movies Games VR
Geometric Modeling Assignment 3: Discrete Differential Quantities
 Geometric Modeling Assignment : Discrete Differential Quantities Acknowledgements: Julian Panetta, Olga Diamanti Assignment (Optional) Topic: Discrete Differential Quantities with libigl Vertex Normals,
Geometric Modeling Assignment : Discrete Differential Quantities Acknowledgements: Julian Panetta, Olga Diamanti Assignment (Optional) Topic: Discrete Differential Quantities with libigl Vertex Normals,
Challenges in large-scale graph processing on HPC platforms and the Graph500 benchmark. by Nkemdirim Dockery
 Challenges in large-scale graph processing on HPC platforms and the Graph500 benchmark by Nkemdirim Dockery High Performance Computing Workloads Core-memory sized Floating point intensive Well-structured
Challenges in large-scale graph processing on HPC platforms and the Graph500 benchmark by Nkemdirim Dockery High Performance Computing Workloads Core-memory sized Floating point intensive Well-structured
Lecture 17: More Fun With Sparse Matrices
 Lecture 17: More Fun With Sparse Matrices David Bindel 26 Oct 2011 Logistics Thanks for info on final project ideas. HW 2 due Monday! Life lessons from HW 2? Where an error occurs may not be where you
Lecture 17: More Fun With Sparse Matrices David Bindel 26 Oct 2011 Logistics Thanks for info on final project ideas. HW 2 due Monday! Life lessons from HW 2? Where an error occurs may not be where you
Automatic Tuning of Sparse Matrix Kernels
 Automatic Tuning of Sparse Matrix Kernels Kathy Yelick U.C. Berkeley and Lawrence Berkeley National Laboratory Richard Vuduc, Lawrence Livermore National Laboratory James Demmel, U.C. Berkeley Berkeley
Automatic Tuning of Sparse Matrix Kernels Kathy Yelick U.C. Berkeley and Lawrence Berkeley National Laboratory Richard Vuduc, Lawrence Livermore National Laboratory James Demmel, U.C. Berkeley Berkeley
Memory Consistency and Multiprocessor Performance
 Memory Consistency Model Memory Consistency and Multiprocessor Performance Define memory correctness for parallel execution Execution appears to the that of some correct execution of some theoretical parallel
Memory Consistency Model Memory Consistency and Multiprocessor Performance Define memory correctness for parallel execution Execution appears to the that of some correct execution of some theoretical parallel
smooth coefficients H. Köstler, U. Rüde
 A robust multigrid solver for the optical flow problem with non- smooth coefficients H. Köstler, U. Rüde Overview Optical Flow Problem Data term and various regularizers A Robust Multigrid Solver Galerkin
A robust multigrid solver for the optical flow problem with non- smooth coefficients H. Köstler, U. Rüde Overview Optical Flow Problem Data term and various regularizers A Robust Multigrid Solver Galerkin
Week 3: MPI. Day 04 :: Domain decomposition, load balancing, hybrid particlemesh
 Week 3: MPI Day 04 :: Domain decomposition, load balancing, hybrid particlemesh methods Domain decompositon Goals of parallel computing Solve a bigger problem Operate on more data (grid points, particles,
Week 3: MPI Day 04 :: Domain decomposition, load balancing, hybrid particlemesh methods Domain decompositon Goals of parallel computing Solve a bigger problem Operate on more data (grid points, particles,
Introduction to Multigrid and its Parallelization
 Introduction to Multigrid and its Parallelization! Thomas D. Economon Lecture 14a May 28, 2014 Announcements 2 HW 1 & 2 have been returned. Any questions? Final projects are due June 11, 5 pm. If you are
Introduction to Multigrid and its Parallelization! Thomas D. Economon Lecture 14a May 28, 2014 Announcements 2 HW 1 & 2 have been returned. Any questions? Final projects are due June 11, 5 pm. If you are
1 2 (3 + x 3) x 2 = 1 3 (3 + x 1 2x 3 ) 1. 3 ( 1 x 2) (3 + x(0) 3 ) = 1 2 (3 + 0) = 3. 2 (3 + x(0) 1 2x (0) ( ) = 1 ( 1 x(0) 2 ) = 1 3 ) = 1 3
 6 Iterative Solvers Lab Objective: Many real-world problems of the form Ax = b have tens of thousands of parameters Solving such systems with Gaussian elimination or matrix factorizations could require
6 Iterative Solvers Lab Objective: Many real-world problems of the form Ax = b have tens of thousands of parameters Solving such systems with Gaussian elimination or matrix factorizations could require
Memory Consistency and Multiprocessor Performance. Adapted from UCB CS252 S01, Copyright 2001 USB
 Memory Consistency and Multiprocessor Performance Adapted from UCB CS252 S01, Copyright 2001 USB 1 Memory Consistency Model Define memory correctness for parallel execution Execution appears to the that
Memory Consistency and Multiprocessor Performance Adapted from UCB CS252 S01, Copyright 2001 USB 1 Memory Consistency Model Define memory correctness for parallel execution Execution appears to the that
PARALLEL METHODS FOR SOLVING PARTIAL DIFFERENTIAL EQUATIONS. Ioana Chiorean
 5 Kragujevac J. Math. 25 (2003) 5 18. PARALLEL METHODS FOR SOLVING PARTIAL DIFFERENTIAL EQUATIONS Ioana Chiorean Babeş-Bolyai University, Department of Mathematics, Cluj-Napoca, Romania (Received May 28,
5 Kragujevac J. Math. 25 (2003) 5 18. PARALLEL METHODS FOR SOLVING PARTIAL DIFFERENTIAL EQUATIONS Ioana Chiorean Babeş-Bolyai University, Department of Mathematics, Cluj-Napoca, Romania (Received May 28,
(Sparse) Linear Solvers
 (Sparse) Linear Solvers Ax = B Why? Many geometry processing applications boil down to: solve one or more linear systems Parameterization Editing Reconstruction Fairing Morphing 2 Don t you just invert
(Sparse) Linear Solvers Ax = B Why? Many geometry processing applications boil down to: solve one or more linear systems Parameterization Editing Reconstruction Fairing Morphing 2 Don t you just invert
Partial Differential Equations
 Simulation in Computer Graphics Partial Differential Equations Matthias Teschner Computer Science Department University of Freiburg Motivation various dynamic effects and physical processes are described
Simulation in Computer Graphics Partial Differential Equations Matthias Teschner Computer Science Department University of Freiburg Motivation various dynamic effects and physical processes are described
ECE 669 Parallel Computer Architecture
 ECE 669 Parallel Computer Architecture Lecture 9 Workload Evaluation Outline Evaluation of applications is important Simulation of sample data sets provides important information Working sets indicate
ECE 669 Parallel Computer Architecture Lecture 9 Workload Evaluation Outline Evaluation of applications is important Simulation of sample data sets provides important information Working sets indicate
Fluent User Services Center
 Solver Settings 5-1 Using the Solver Setting Solver Parameters Convergence Definition Monitoring Stability Accelerating Convergence Accuracy Grid Independence Adaption Appendix: Background Finite Volume
Solver Settings 5-1 Using the Solver Setting Solver Parameters Convergence Definition Monitoring Stability Accelerating Convergence Accuracy Grid Independence Adaption Appendix: Background Finite Volume
AMS526: Numerical Analysis I (Numerical Linear Algebra)
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 5: Sparse Linear Systems and Factorization Methods Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical Analysis I 1 / 18 Sparse
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 5: Sparse Linear Systems and Factorization Methods Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical Analysis I 1 / 18 Sparse
EE795: Computer Vision and Intelligent Systems
 EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 FDH 204 Lecture 14 130307 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Stereo Dense Motion Estimation Translational
EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 FDH 204 Lecture 14 130307 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Stereo Dense Motion Estimation Translational
High Performance Computing Programming Paradigms and Scalability Part 6: Examples of Parallel Algorithms
 High Performance Computing Programming Paradigms and Scalability Part 6: Examples of Parallel Algorithms PD Dr. rer. nat. habil. Ralf-Peter Mundani Computation in Engineering (CiE) Scientific Computing
High Performance Computing Programming Paradigms and Scalability Part 6: Examples of Parallel Algorithms PD Dr. rer. nat. habil. Ralf-Peter Mundani Computation in Engineering (CiE) Scientific Computing
Principle Of Parallel Algorithm Design (cont.) Alexandre David B2-206
 Principle Of Parallel Algorithm Design (cont.) Alexandre David B2-206 1 Today Characteristics of Tasks and Interactions (3.3). Mapping Techniques for Load Balancing (3.4). Methods for Containing Interaction
Principle Of Parallel Algorithm Design (cont.) Alexandre David B2-206 1 Today Characteristics of Tasks and Interactions (3.3). Mapping Techniques for Load Balancing (3.4). Methods for Containing Interaction
The Fast Multipole Method (FMM)
 The Fast Multipole Method (FMM) Motivation for FMM Computational Physics Problems involving mutual interactions of N particles Gravitational or Electrostatic forces Collective (but weak) long-range forces
The Fast Multipole Method (FMM) Motivation for FMM Computational Physics Problems involving mutual interactions of N particles Gravitational or Electrostatic forces Collective (but weak) long-range forces
Parallel Combinatorial BLAS and Applications in Graph Computations
 Parallel Combinatorial BLAS and Applications in Graph Computations Aydın Buluç John R. Gilbert University of California, Santa Barbara SIAM ANNUAL MEETING 2009 July 8, 2009 1 Primitives for Graph Computations
Parallel Combinatorial BLAS and Applications in Graph Computations Aydın Buluç John R. Gilbert University of California, Santa Barbara SIAM ANNUAL MEETING 2009 July 8, 2009 1 Primitives for Graph Computations
Multigrid. James Demmel. Poisson s equation in 1D: T = Graph and stencil. 2 u/ x 2 = f(x)
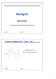 Multigrid James Demmel www.cs.berkeley.edu/~demmel/ma221_spr16 Poisson s equation in 1D: 2 u/ x 2 = f(x) T = 2-1 -1 2-1 -1 2-1 -1 2-1 -1 2 Graph and stencil -1 2-1 1 2D Poisson s equation Similar to the
Multigrid James Demmel www.cs.berkeley.edu/~demmel/ma221_spr16 Poisson s equation in 1D: 2 u/ x 2 = f(x) T = 2-1 -1 2-1 -1 2-1 -1 2-1 -1 2 Graph and stencil -1 2-1 1 2D Poisson s equation Similar to the
Mass-Spring Systems. Last Time?
 Mass-Spring Systems Last Time? Implicit Surfaces & Marching Cubes/Tetras Collision Detection & Conservative Bounding Regions Spatial Acceleration Data Structures Octree, k-d tree, BSF tree 1 Today Particle
Mass-Spring Systems Last Time? Implicit Surfaces & Marching Cubes/Tetras Collision Detection & Conservative Bounding Regions Spatial Acceleration Data Structures Octree, k-d tree, BSF tree 1 Today Particle
Numerical Algorithms
 Chapter 10 Slide 464 Numerical Algorithms Slide 465 Numerical Algorithms In textbook do: Matrix multiplication Solving a system of linear equations Slide 466 Matrices A Review An n m matrix Column a 0,0
Chapter 10 Slide 464 Numerical Algorithms Slide 465 Numerical Algorithms In textbook do: Matrix multiplication Solving a system of linear equations Slide 466 Matrices A Review An n m matrix Column a 0,0
Programming as Successive Refinement. Partitioning for Performance
 Programming as Successive Refinement Not all issues dealt with up front Partitioning often independent of architecture, and done first View machine as a collection of communicating processors balancing
Programming as Successive Refinement Not all issues dealt with up front Partitioning often independent of architecture, and done first View machine as a collection of communicating processors balancing
Lecture 2: Parallel Programs. Topics: consistency, parallel applications, parallelization process
 Lecture 2: Parallel Programs Topics: consistency, parallel applications, parallelization process 1 Sequential Consistency A multiprocessor is sequentially consistent if the result of the execution is achievable
Lecture 2: Parallel Programs Topics: consistency, parallel applications, parallelization process 1 Sequential Consistency A multiprocessor is sequentially consistent if the result of the execution is achievable
CSCE 5160 Parallel Processing. CSCE 5160 Parallel Processing
 HW #9 10., 10.3, 10.7 Due April 17 { } Review Completing Graph Algorithms Maximal Independent Set Johnson s shortest path algorithm using adjacency lists Q= V; for all v in Q l[v] = infinity; l[s] = 0;
HW #9 10., 10.3, 10.7 Due April 17 { } Review Completing Graph Algorithms Maximal Independent Set Johnson s shortest path algorithm using adjacency lists Q= V; for all v in Q l[v] = infinity; l[s] = 0;
Lecture 5. Applications: N-body simulation, sorting, stencil methods
 Lecture 5 Applications: N-body simulation, sorting, stencil methods Announcements Quiz #1 in section on 10/13 Midterm: evening of 10/30, 7:00 to 8:20 PM In Assignment 2, the following variation is suggested
Lecture 5 Applications: N-body simulation, sorting, stencil methods Announcements Quiz #1 in section on 10/13 Midterm: evening of 10/30, 7:00 to 8:20 PM In Assignment 2, the following variation is suggested
Contents. I The Basic Framework for Stationary Problems 1
 page v Preface xiii I The Basic Framework for Stationary Problems 1 1 Some model PDEs 3 1.1 Laplace s equation; elliptic BVPs... 3 1.1.1 Physical experiments modeled by Laplace s equation... 5 1.2 Other
page v Preface xiii I The Basic Framework for Stationary Problems 1 1 Some model PDEs 3 1.1 Laplace s equation; elliptic BVPs... 3 1.1.1 Physical experiments modeled by Laplace s equation... 5 1.2 Other
Outline. Parallel Algorithms for Linear Algebra. Number of Processors and Problem Size. Speedup and Efficiency
 1 2 Parallel Algorithms for Linear Algebra Richard P. Brent Computer Sciences Laboratory Australian National University Outline Basic concepts Parallel architectures Practical design issues Programming
1 2 Parallel Algorithms for Linear Algebra Richard P. Brent Computer Sciences Laboratory Australian National University Outline Basic concepts Parallel architectures Practical design issues Programming
ECE 259 / CPS 221 Advanced Computer Architecture II (Parallel Computer Architecture) Parallel Programming
 ECE 259 / CPS 221 Advanced Computer Architecture II (Parallel Computer Architecture) Parallel Programming Copyright 2010 Daniel J. Sorin Duke University Slides are derived from work by Sarita Adve (Illinois),
ECE 259 / CPS 221 Advanced Computer Architecture II (Parallel Computer Architecture) Parallel Programming Copyright 2010 Daniel J. Sorin Duke University Slides are derived from work by Sarita Adve (Illinois),
Lesson 2 7 Graph Partitioning
 Lesson 2 7 Graph Partitioning The Graph Partitioning Problem Look at the problem from a different angle: Let s multiply a sparse matrix A by a vector X. Recall the duality between matrices and graphs:
Lesson 2 7 Graph Partitioning The Graph Partitioning Problem Look at the problem from a different angle: Let s multiply a sparse matrix A by a vector X. Recall the duality between matrices and graphs:
Particle-based Fluid Simulation
 Simulation in Computer Graphics Particle-based Fluid Simulation Matthias Teschner Computer Science Department University of Freiburg Application (with Pixar) 10 million fluid + 4 million rigid particles,
Simulation in Computer Graphics Particle-based Fluid Simulation Matthias Teschner Computer Science Department University of Freiburg Application (with Pixar) 10 million fluid + 4 million rigid particles,
Parallelization Strategy
 COSC 335 Software Design Parallel Design Patterns (II) Spring 2008 Parallelization Strategy Finding Concurrency Structure the problem to expose exploitable concurrency Algorithm Structure Supporting Structure
COSC 335 Software Design Parallel Design Patterns (II) Spring 2008 Parallelization Strategy Finding Concurrency Structure the problem to expose exploitable concurrency Algorithm Structure Supporting Structure
Space Filling Curves and Hierarchical Basis. Klaus Speer
 Space Filling Curves and Hierarchical Basis Klaus Speer Abstract Real world phenomena can be best described using differential equations. After linearisation we have to deal with huge linear systems of
Space Filling Curves and Hierarchical Basis Klaus Speer Abstract Real world phenomena can be best described using differential equations. After linearisation we have to deal with huge linear systems of
ME964 High Performance Computing for Engineering Applications
 ME964 High Performance Computing for Engineering Applications Outlining Midterm Projects Topic 3: GPU-based FEA Topic 4: GPU Direct Solver for Sparse Linear Algebra March 01, 2011 Dan Negrut, 2011 ME964
ME964 High Performance Computing for Engineering Applications Outlining Midterm Projects Topic 3: GPU-based FEA Topic 4: GPU Direct Solver for Sparse Linear Algebra March 01, 2011 Dan Negrut, 2011 ME964
6. Parallel Volume Rendering Algorithms
 6. Parallel Volume Algorithms This chapter introduces a taxonomy of parallel volume rendering algorithms. In the thesis statement we claim that parallel algorithms may be described by "... how the tasks
6. Parallel Volume Algorithms This chapter introduces a taxonomy of parallel volume rendering algorithms. In the thesis statement we claim that parallel algorithms may be described by "... how the tasks
An Efficient CUDA Implementation of a Tree-Based N-Body Algorithm. Martin Burtscher Department of Computer Science Texas State University-San Marcos
 An Efficient CUDA Implementation of a Tree-Based N-Body Algorithm Martin Burtscher Department of Computer Science Texas State University-San Marcos Mapping Regular Code to GPUs Regular codes Operate on
An Efficient CUDA Implementation of a Tree-Based N-Body Algorithm Martin Burtscher Department of Computer Science Texas State University-San Marcos Mapping Regular Code to GPUs Regular codes Operate on
1.2 Numerical Solutions of Flow Problems
 1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
Realtime Water Simulation on GPU. Nuttapong Chentanez NVIDIA Research
 1 Realtime Water Simulation on GPU Nuttapong Chentanez NVIDIA Research 2 3 Overview Approaches to realtime water simulation Hybrid shallow water solver + particles Hybrid 3D tall cell water solver + particles
1 Realtime Water Simulation on GPU Nuttapong Chentanez NVIDIA Research 2 3 Overview Approaches to realtime water simulation Hybrid shallow water solver + particles Hybrid 3D tall cell water solver + particles
Advanced Surface Based MoM Techniques for Packaging and Interconnect Analysis
 Electrical Interconnect and Packaging Advanced Surface Based MoM Techniques for Packaging and Interconnect Analysis Jason Morsey Barry Rubin, Lijun Jiang, Lon Eisenberg, Alina Deutsch Introduction Fast
Electrical Interconnect and Packaging Advanced Surface Based MoM Techniques for Packaging and Interconnect Analysis Jason Morsey Barry Rubin, Lijun Jiang, Lon Eisenberg, Alina Deutsch Introduction Fast
Fast methods for N-body problems
 CME342- Parallel Methods in Numerical Analysis Fast methods for N-body problems May 21, 2014 Lecture 13 Outline Motivation: N-body problem is O(N^2) Data structures: quad tree and oct tree (ADT?) The Barnes-Hut
CME342- Parallel Methods in Numerical Analysis Fast methods for N-body problems May 21, 2014 Lecture 13 Outline Motivation: N-body problem is O(N^2) Data structures: quad tree and oct tree (ADT?) The Barnes-Hut
GTC 2013: DEVELOPMENTS IN GPU-ACCELERATED SPARSE LINEAR ALGEBRA ALGORITHMS. Kyle Spagnoli. Research EM Photonics 3/20/2013
 GTC 2013: DEVELOPMENTS IN GPU-ACCELERATED SPARSE LINEAR ALGEBRA ALGORITHMS Kyle Spagnoli Research Engineer @ EM Photonics 3/20/2013 INTRODUCTION» Sparse systems» Iterative solvers» High level benchmarks»
GTC 2013: DEVELOPMENTS IN GPU-ACCELERATED SPARSE LINEAR ALGEBRA ALGORITHMS Kyle Spagnoli Research Engineer @ EM Photonics 3/20/2013 INTRODUCTION» Sparse systems» Iterative solvers» High level benchmarks»
Visual Tracking (1) Tracking of Feature Points and Planar Rigid Objects
 Intelligent Control Systems Visual Tracking (1) Tracking of Feature Points and Planar Rigid Objects Shingo Kagami Graduate School of Information Sciences, Tohoku University swk(at)ic.is.tohoku.ac.jp http://www.ic.is.tohoku.ac.jp/ja/swk/
Intelligent Control Systems Visual Tracking (1) Tracking of Feature Points and Planar Rigid Objects Shingo Kagami Graduate School of Information Sciences, Tohoku University swk(at)ic.is.tohoku.ac.jp http://www.ic.is.tohoku.ac.jp/ja/swk/
Algorithms, System and Data Centre Optimisation for Energy Efficient HPC
 2015-09-14 Algorithms, System and Data Centre Optimisation for Energy Efficient HPC Vincent Heuveline URZ Computing Centre of Heidelberg University EMCL Engineering Mathematics and Computing Lab 1 Energy
2015-09-14 Algorithms, System and Data Centre Optimisation for Energy Efficient HPC Vincent Heuveline URZ Computing Centre of Heidelberg University EMCL Engineering Mathematics and Computing Lab 1 Energy
6 February Parallel Computing: A View From Berkeley. E. M. Hielscher. Introduction. Applications and Dwarfs. Hardware. Programming Models
 Parallel 6 February 2008 Motivation All major processor manufacturers have switched to parallel architectures This switch driven by three Walls : the Power Wall, Memory Wall, and ILP Wall Power = Capacitance
Parallel 6 February 2008 Motivation All major processor manufacturers have switched to parallel architectures This switch driven by three Walls : the Power Wall, Memory Wall, and ILP Wall Power = Capacitance
Efficient Multi-GPU CUDA Linear Solvers for OpenFOAM
 Efficient Multi-GPU CUDA Linear Solvers for OpenFOAM Alexander Monakov, amonakov@ispras.ru Institute for System Programming of Russian Academy of Sciences March 20, 2013 1 / 17 Problem Statement In OpenFOAM,
Efficient Multi-GPU CUDA Linear Solvers for OpenFOAM Alexander Monakov, amonakov@ispras.ru Institute for System Programming of Russian Academy of Sciences March 20, 2013 1 / 17 Problem Statement In OpenFOAM,
Matrix Multiplication
 Matrix Multiplication CPS343 Parallel and High Performance Computing Spring 2013 CPS343 (Parallel and HPC) Matrix Multiplication Spring 2013 1 / 32 Outline 1 Matrix operations Importance Dense and sparse
Matrix Multiplication CPS343 Parallel and High Performance Computing Spring 2013 CPS343 (Parallel and HPC) Matrix Multiplication Spring 2013 1 / 32 Outline 1 Matrix operations Importance Dense and sparse
Using GPUs to compute the multilevel summation of electrostatic forces
 Using GPUs to compute the multilevel summation of electrostatic forces David J. Hardy Theoretical and Computational Biophysics Group Beckman Institute for Advanced Science and Technology University of
Using GPUs to compute the multilevel summation of electrostatic forces David J. Hardy Theoretical and Computational Biophysics Group Beckman Institute for Advanced Science and Technology University of
Multi-Domain Pattern. I. Problem. II. Driving Forces. III. Solution
 Multi-Domain Pattern I. Problem The problem represents computations characterized by an underlying system of mathematical equations, often simulating behaviors of physical objects through discrete time
Multi-Domain Pattern I. Problem The problem represents computations characterized by an underlying system of mathematical equations, often simulating behaviors of physical objects through discrete time
TAU mesh deformation. Thomas Gerhold
 TAU mesh deformation Thomas Gerhold The parallel mesh deformation of the DLR TAU-Code Introduction Mesh deformation method & Parallelization Results & Applications Conclusion & Outlook Introduction CFD
TAU mesh deformation Thomas Gerhold The parallel mesh deformation of the DLR TAU-Code Introduction Mesh deformation method & Parallelization Results & Applications Conclusion & Outlook Introduction CFD
Design of Parallel Algorithms. Models of Parallel Computation
 + Design of Parallel Algorithms Models of Parallel Computation + Chapter Overview: Algorithms and Concurrency n Introduction to Parallel Algorithms n Tasks and Decomposition n Processes and Mapping n Processes
+ Design of Parallel Algorithms Models of Parallel Computation + Chapter Overview: Algorithms and Concurrency n Introduction to Parallel Algorithms n Tasks and Decomposition n Processes and Mapping n Processes
An introduction to mesh generation Part IV : elliptic meshing
 Elliptic An introduction to mesh generation Part IV : elliptic meshing Department of Civil Engineering, Université catholique de Louvain, Belgium Elliptic Curvilinear Meshes Basic concept A curvilinear
Elliptic An introduction to mesh generation Part IV : elliptic meshing Department of Civil Engineering, Université catholique de Louvain, Belgium Elliptic Curvilinear Meshes Basic concept A curvilinear
CS-184: Computer Graphics Lecture #21: Fluid Simulation II
 CS-184: Computer Graphics Lecture #21: Fluid Simulation II Rahul Narain University of California, Berkeley Nov. 18 19, 2013 Grid-based fluid simulation Recap: Eulerian viewpoint Grid is fixed, fluid moves
CS-184: Computer Graphics Lecture #21: Fluid Simulation II Rahul Narain University of California, Berkeley Nov. 18 19, 2013 Grid-based fluid simulation Recap: Eulerian viewpoint Grid is fixed, fluid moves
Introduction to parallel Computing
 Introduction to parallel Computing VI-SEEM Training Paschalis Paschalis Korosoglou Korosoglou (pkoro@.gr) (pkoro@.gr) Outline Serial vs Parallel programming Hardware trends Why HPC matters HPC Concepts
Introduction to parallel Computing VI-SEEM Training Paschalis Paschalis Korosoglou Korosoglou (pkoro@.gr) (pkoro@.gr) Outline Serial vs Parallel programming Hardware trends Why HPC matters HPC Concepts
Visual Tracking (1) Feature Point Tracking and Block Matching
 Intelligent Control Systems Visual Tracking (1) Feature Point Tracking and Block Matching Shingo Kagami Graduate School of Information Sciences, Tohoku University swk(at)ic.is.tohoku.ac.jp http://www.ic.is.tohoku.ac.jp/ja/swk/
Intelligent Control Systems Visual Tracking (1) Feature Point Tracking and Block Matching Shingo Kagami Graduate School of Information Sciences, Tohoku University swk(at)ic.is.tohoku.ac.jp http://www.ic.is.tohoku.ac.jp/ja/swk/
SELECTIVE ALGEBRAIC MULTIGRID IN FOAM-EXTEND
 Student Submission for the 5 th OpenFOAM User Conference 2017, Wiesbaden - Germany: SELECTIVE ALGEBRAIC MULTIGRID IN FOAM-EXTEND TESSA UROIĆ Faculty of Mechanical Engineering and Naval Architecture, Ivana
Student Submission for the 5 th OpenFOAM User Conference 2017, Wiesbaden - Germany: SELECTIVE ALGEBRAIC MULTIGRID IN FOAM-EXTEND TESSA UROIĆ Faculty of Mechanical Engineering and Naval Architecture, Ivana
GPU-based Distributed Behavior Models with CUDA
 GPU-based Distributed Behavior Models with CUDA Courtesy: YouTube, ISIS Lab, Universita degli Studi di Salerno Bradly Alicea Introduction Flocking: Reynolds boids algorithm. * models simple local behaviors
GPU-based Distributed Behavior Models with CUDA Courtesy: YouTube, ISIS Lab, Universita degli Studi di Salerno Bradly Alicea Introduction Flocking: Reynolds boids algorithm. * models simple local behaviors
Parallel Computing. Parallel Algorithm Design
 Parallel Computing Parallel Algorithm Design Task/Channel Model Parallel computation = set of tasks Task Program Local memory Collection of I/O ports Tasks interact by sending messages through channels
Parallel Computing Parallel Algorithm Design Task/Channel Model Parallel computation = set of tasks Task Program Local memory Collection of I/O ports Tasks interact by sending messages through channels
PARALLELIZATION OF POTENTIAL FLOW SOLVER USING PC CLUSTERS
 Proceedings of FEDSM 2000: ASME Fluids Engineering Division Summer Meeting June 11-15,2000, Boston, MA FEDSM2000-11223 PARALLELIZATION OF POTENTIAL FLOW SOLVER USING PC CLUSTERS Prof. Blair.J.Perot Manjunatha.N.
Proceedings of FEDSM 2000: ASME Fluids Engineering Division Summer Meeting June 11-15,2000, Boston, MA FEDSM2000-11223 PARALLELIZATION OF POTENTIAL FLOW SOLVER USING PC CLUSTERS Prof. Blair.J.Perot Manjunatha.N.
(Lec 14) Placement & Partitioning: Part III
 Page (Lec ) Placement & Partitioning: Part III What you know That there are big placement styles: iterative, recursive, direct Placement via iterative improvement using simulated annealing Recursive-style
Page (Lec ) Placement & Partitioning: Part III What you know That there are big placement styles: iterative, recursive, direct Placement via iterative improvement using simulated annealing Recursive-style
Lecture 4: Principles of Parallel Algorithm Design (part 4)
 Lecture 4: Principles of Parallel Algorithm Design (part 4) 1 Mapping Technique for Load Balancing Minimize execution time Reduce overheads of execution Sources of overheads: Inter-process interaction
Lecture 4: Principles of Parallel Algorithm Design (part 4) 1 Mapping Technique for Load Balancing Minimize execution time Reduce overheads of execution Sources of overheads: Inter-process interaction
Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Computation in Astrophysics Seminar (Spring 2006) L. J. Dursi
 Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Eulerian Grid Methods The methods covered so far in this course use an Eulerian grid: Prescribed coordinates In `lab frame' Fluid elements flow
Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Eulerian Grid Methods The methods covered so far in this course use an Eulerian grid: Prescribed coordinates In `lab frame' Fluid elements flow
Matrix Multiplication
 Matrix Multiplication CPS343 Parallel and High Performance Computing Spring 2018 CPS343 (Parallel and HPC) Matrix Multiplication Spring 2018 1 / 32 Outline 1 Matrix operations Importance Dense and sparse
Matrix Multiplication CPS343 Parallel and High Performance Computing Spring 2018 CPS343 (Parallel and HPC) Matrix Multiplication Spring 2018 1 / 32 Outline 1 Matrix operations Importance Dense and sparse
Contents. Preface xvii Acknowledgments. CHAPTER 1 Introduction to Parallel Computing 1. CHAPTER 2 Parallel Programming Platforms 11
 Preface xvii Acknowledgments xix CHAPTER 1 Introduction to Parallel Computing 1 1.1 Motivating Parallelism 2 1.1.1 The Computational Power Argument from Transistors to FLOPS 2 1.1.2 The Memory/Disk Speed
Preface xvii Acknowledgments xix CHAPTER 1 Introduction to Parallel Computing 1 1.1 Motivating Parallelism 2 1.1.1 The Computational Power Argument from Transistors to FLOPS 2 1.1.2 The Memory/Disk Speed
1 Serial Implementation
 Grey Ballard, Razvan Carbunescu, Andrew Gearhart, Mehrzad Tartibi CS267: Homework 2 1 Serial Implementation For n particles, the original code requires O(n 2 ) time because at each time step, the apply
Grey Ballard, Razvan Carbunescu, Andrew Gearhart, Mehrzad Tartibi CS267: Homework 2 1 Serial Implementation For n particles, the original code requires O(n 2 ) time because at each time step, the apply
Auto Injector Syringe. A Fluent Dynamic Mesh 1DOF Tutorial
 Auto Injector Syringe A Fluent Dynamic Mesh 1DOF Tutorial 1 2015 ANSYS, Inc. June 26, 2015 Prerequisites This tutorial is written with the assumption that You have attended the Introduction to ANSYS Fluent
Auto Injector Syringe A Fluent Dynamic Mesh 1DOF Tutorial 1 2015 ANSYS, Inc. June 26, 2015 Prerequisites This tutorial is written with the assumption that You have attended the Introduction to ANSYS Fluent
Numerical Methods for (Time-Dependent) HJ PDEs
 Numerical Methods for (Time-Dependent) HJ PDEs Ian Mitchell Department of Computer Science The University of British Columbia research supported by National Science and Engineering Research Council of
Numerical Methods for (Time-Dependent) HJ PDEs Ian Mitchell Department of Computer Science The University of British Columbia research supported by National Science and Engineering Research Council of
Application of Finite Volume Method for Structural Analysis
 Application of Finite Volume Method for Structural Analysis Saeed-Reza Sabbagh-Yazdi and Milad Bayatlou Associate Professor, Civil Engineering Department of KNToosi University of Technology, PostGraduate
Application of Finite Volume Method for Structural Analysis Saeed-Reza Sabbagh-Yazdi and Milad Bayatlou Associate Professor, Civil Engineering Department of KNToosi University of Technology, PostGraduate
Master Informatics Eng.
 Advanced Architectures Master Informatics Eng. 207/8 A.J.Proença The Roofline Performance Model (most slides are borrowed) AJProença, Advanced Architectures, MiEI, UMinho, 207/8 AJProença, Advanced Architectures,
Advanced Architectures Master Informatics Eng. 207/8 A.J.Proença The Roofline Performance Model (most slides are borrowed) AJProença, Advanced Architectures, MiEI, UMinho, 207/8 AJProença, Advanced Architectures,
