Appendix E Calculating Normal Vectors
|
|
|
- Jordan Blair
- 5 years ago
- Views:
Transcription
1 OpenGL Programming Guide (Addison-Wesley Publishing Company) Appendix E Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use the OpenGL lighting facility, which is described in Chapter 5. "Normal Vectors" in Chapter 2 introduces normals and the OpenGL command for specifying them. This appendix goes through the details of calculating them. It has the following major sections: "Finding Normals for Analytic Surfaces" "Finding Normals from Polygonal Data" Since normals are perpendicular to a surface, you can find the normal at a particular point on a surface by first finding the flat plane that just touches the surface at that point. The normal is the vector that s perpendicular to that plane. On a perfect sphere, for example, the normal at a point on the surface is in the same direction as the vector from the center of the sphere to that point. For other types of surfaces, there are other, better means for determining the normals, depending on how the surface is specified. Recall that smooth curved surfaces are approximated by a large number of small flat polygons. If the vectors perpendicular to these polygons are used as the surface normals in such an approximation, the surface appears faceted, since the normal direction is discontinuous across the polygonal boundaries. In many cases, however, an exact mathematical description exists for the surface, and true surface normals can be calculated at every point. Using the true normals improves the rendering considerably, as shown in Figure E-1. Even if you don t have a mathematical description, you can do better than the faceted look shown in the figure. The two major sections in this appendix describe how to calculate normal vectors for these two cases: "Finding Normals for Analytic Surfaces" explains what to do when you have a mathematical description of a surface. "Finding Normals from Polygonal Data" covers the case when you have only the polygonal data to describe a surface. Figure E-1 : Rendering with Polygonal Normals vs. True Normals
2 Finding Normals for Analytic Surfaces Analytic surfaces are smooth, differentiable surfaces that are described by a mathematical equation (or set of equations). In many cases, the easiest surfaces to find normals for are analytic surfaces for which you have an explicit definition in the following form: V(s,t) = [ X(s,t) Y(s,t) Z(s,t) ] where s and t are constrained to be in some domain, and X, Y, and Z are differentiable functions of two variables. To calculate the normal, find which are vectors tangent to the surface in the s and t directions. The cross product is perpendicular to both and, hence, to the surface. The following shows how to calculate the cross product of two vectors. (Watch out for the degenerate cases where the cross product has zero length!) You should probably normalize the resulting vector. To normalize a vector [x y z], calculate its length and divide each component of the vector by the length. As an example of these calculations, consider the analytic surface V(s,t) = [ s2 t3 3-st ] From this we have So, for example, when s=1 and t=2, the corresponding point on the surface is (1, 8, 1), and the vector (-24, 2, 24) is perpendicular to the surface at that point. The length of this vector is 34, so the unit normal vector is (-24/34, 2/34, 24/34) = ( , , ).
3 For analytic surfaces that are described implicitly, as F(x, y, z) = 0, the problem is harder. In some cases, you can solve for one of the variables, say z = G(x, y), and put it in the explicit form given previously: Then continue as described earlier. If you can t get the surface equation in an explicit form, you might be able to make use of the fact that the normal vector is given by the gradient evaluated at a particular point (x, y, z). Calculating the gradient might be easy, but finding a point that lies on the surface can be difficult. As an example of an implicitly defined analytic function, consider the equation of a sphere of radius 1 centered at the origin: x2 + y2 + z2-1 = 0 ) This means that F (x, y, z) = x2 + y2 + z2-1 which can be solved for z to yield Thus, normals can be calculated from the explicit form as described previously. If you could not solve for z, you could have used the gradient as long as you could find a point on the surface. In this case, it s not so hard to find a point - for example, (2/3, 1/3, 2/3) lies on the surface. Using the gradient, the normal at this point is (4/3, 2/3, 4/3). The unit-length normal is (2/3, 1/3, 2/3), which is the same as the point on the surface, as expected. Finding Normals from Polygonal Data
4 As mentioned previously, you often want to find normals for surfaces that are described with polygonal data such that the surfaces appear smooth rather than faceted. In most cases, the easiest way for you to do this (though it might not be the most efficient way) is to calculate the normal vectors for each of the polygonal facets and then to average the normals for neighboring facets. Use the averaged normal for the vertex that the neighboring facets have in common. Figure E-2 shows a surface and its polygonal approximation. (Of course, if the polygons represent the exact surface and aren t merely an approximation - if you re drawing a cube or a cut diamond, for example - don t do the averaging. Calculate the normal for each facet as described in the following paragraphs, and use that same normal for each vertex of the facet.) Figure E-2 : Averaging Normal Vectors To find the normal for a flat polygon, take any three vertices v1, v2, and v3 of the polygon that do not lie in a straight line. The cross product [v1 - v2] [v2 - v3] is perpendicular to the polygon. (Typically, you want to normalize the resulting vector.) Then you need to average the normals for adjoining facets to avoid giving too much weight to one of them. For instance, in the example shown in Figure E-2, if n1, n2, n3, and n4 are the normals for the four polygons meeting at point P, calculate n1+n2+n3+n4 and then normalize it. (You can get a better average if you weight the normals by the size of the angles at the shared intersection.) The resulting
5 vector can be used as the normal for point P. Sometimes, you need to vary this method for particular situations. For instance, at the boundary of a surface (for example, point Q in Figure E-2), you might be able to choose a better normal based on your knowledge of what the surface should look like. Sometimes the best you can do is to average the polygon normals on the boundary as well. Similarly, some models have some smooth parts and some sharp corners (point R is on such an edge in Figure E-2). In this case, the normals on either side of the crease shouldn t be averaged. Instead, polygons on one side of the crease should be drawn with one normal, and polygons on the other side with another. OpenGL Programming Guide (Addison-Wesley Publishing Company)
Let and be a differentiable function. Let Then be the level surface given by
 Module 12 : Total differential, Tangent planes and normals Lecture 35 : Tangent plane and normal [Section 35.1] > Objectives In this section you will learn the following : The notion tangent plane to a
Module 12 : Total differential, Tangent planes and normals Lecture 35 : Tangent plane and normal [Section 35.1] > Objectives In this section you will learn the following : The notion tangent plane to a
Curves and Surfaces Computer Graphics I Lecture 9
 15-462 Computer Graphics I Lecture 9 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] February 19, 2002 Frank Pfenning Carnegie
15-462 Computer Graphics I Lecture 9 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] February 19, 2002 Frank Pfenning Carnegie
Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers
 In this section we present Lagrange s method for maximizing or minimizing a general function f(x, y, z) subject to a constraint (or side condition) of the form g(x, y, z) = k. Figure 1 shows this curve
In this section we present Lagrange s method for maximizing or minimizing a general function f(x, y, z) subject to a constraint (or side condition) of the form g(x, y, z) = k. Figure 1 shows this curve
Central issues in modelling
 Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction includes: manual modelling; fitting to
Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction includes: manual modelling; fitting to
Advanced Algebra. Equation of a Circle
 Advanced Algebra Equation of a Circle Task on Entry Plotting Equations Using the table and axis below, plot the graph for - x 2 + y 2 = 25 x -5-4 -3 0 3 4 5 y 1 4 y 2-4 3 2 + y 2 = 25 9 + y 2 = 25 y 2
Advanced Algebra Equation of a Circle Task on Entry Plotting Equations Using the table and axis below, plot the graph for - x 2 + y 2 = 25 x -5-4 -3 0 3 4 5 y 1 4 y 2-4 3 2 + y 2 = 25 9 + y 2 = 25 y 2
Curves D.A. Forsyth, with slides from John Hart
 Curves D.A. Forsyth, with slides from John Hart Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction
Curves D.A. Forsyth, with slides from John Hart Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction
TANGENTS AND NORMALS
 Mathematics Revision Guides Tangents and Normals Page 1 of 8 MK HOME TUITION Mathematics Revision Guides Level: AS / A Level AQA : C1 Edecel: C OCR: C1 OCR MEI: C TANGENTS AND NORMALS Version : 1 Date:
Mathematics Revision Guides Tangents and Normals Page 1 of 8 MK HOME TUITION Mathematics Revision Guides Level: AS / A Level AQA : C1 Edecel: C OCR: C1 OCR MEI: C TANGENTS AND NORMALS Version : 1 Date:
The Law of Reflection
 If the surface off which the light is reflected is smooth, then the light undergoes specular reflection (parallel rays will all be reflected in the same directions). If, on the other hand, the surface
If the surface off which the light is reflected is smooth, then the light undergoes specular reflection (parallel rays will all be reflected in the same directions). If, on the other hand, the surface
Surfaces and Partial Derivatives
 Surfaces and James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 15, 2017 Outline 1 2 Tangent Planes Let s go back to our simple surface
Surfaces and James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 15, 2017 Outline 1 2 Tangent Planes Let s go back to our simple surface
Haga's Origamics. Haga's Origamics are a series of activities designed to illustrate the science behind simple paper folding.
 Haga's Origamics Haga's Origamics are a series of activities designed to illustrate the science behind simple paper folding. Activity I : TUPS (Turned-Up Parts) Take a square piece of paper and label the
Haga's Origamics Haga's Origamics are a series of activities designed to illustrate the science behind simple paper folding. Activity I : TUPS (Turned-Up Parts) Take a square piece of paper and label the
Intro to Modeling Modeling in 3D
 Intro to Modeling Modeling in 3D Polygon sets can approximate more complex shapes as discretized surfaces 2 1 2 3 Curve surfaces in 3D Sphere, ellipsoids, etc Curved Surfaces Modeling in 3D ) ( 2 2 2 2
Intro to Modeling Modeling in 3D Polygon sets can approximate more complex shapes as discretized surfaces 2 1 2 3 Curve surfaces in 3D Sphere, ellipsoids, etc Curved Surfaces Modeling in 3D ) ( 2 2 2 2
Licom Systems Ltd., Training Course Notes. 3D Surface Creation
 , Training Course Notes Work Volume and Work Planes...........................1 Overview..........................................1 Work Volume....................................1 Work Plane......................................1
, Training Course Notes Work Volume and Work Planes...........................1 Overview..........................................1 Work Volume....................................1 Work Plane......................................1
Curves and Surfaces Computer Graphics I Lecture 10
 15-462 Computer Graphics I Lecture 10 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] September 30, 2003 Doug James Carnegie
15-462 Computer Graphics I Lecture 10 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] September 30, 2003 Doug James Carnegie
Answer Key: Three-Dimensional Cross Sections
 Geometry A Unit Answer Key: Three-Dimensional Cross Sections Name Date Objectives In this lesson, you will: visualize three-dimensional objects from different perspectives be able to create a projection
Geometry A Unit Answer Key: Three-Dimensional Cross Sections Name Date Objectives In this lesson, you will: visualize three-dimensional objects from different perspectives be able to create a projection
Surfaces and Integral Curves
 MODULE 1: MATHEMATICAL PRELIMINARIES 16 Lecture 3 Surfaces and Integral Curves In Lecture 3, we recall some geometrical concepts that are essential for understanding the nature of solutions of partial
MODULE 1: MATHEMATICAL PRELIMINARIES 16 Lecture 3 Surfaces and Integral Curves In Lecture 3, we recall some geometrical concepts that are essential for understanding the nature of solutions of partial
What you will learn today
 What you will learn today Tangent Planes and Linear Approximation and the Gradient Vector Vector Functions 1/21 Recall in one-variable calculus, as we zoom in toward a point on a curve, the graph becomes
What you will learn today Tangent Planes and Linear Approximation and the Gradient Vector Vector Functions 1/21 Recall in one-variable calculus, as we zoom in toward a point on a curve, the graph becomes
1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral
 1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral Show your working and give your answer correct to three decimal places. 2 2.5 3 3.5 4 When When When When When
1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral Show your working and give your answer correct to three decimal places. 2 2.5 3 3.5 4 When When When When When
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Surface Rendering. Surface Rendering
 Surface Rendering Surface Rendering Introduce Mapping Methods - Texture Mapping - Environmental Mapping - Bump Mapping Go over strategies for - Forward vs backward mapping 2 1 The Limits of Geometric Modeling
Surface Rendering Surface Rendering Introduce Mapping Methods - Texture Mapping - Environmental Mapping - Bump Mapping Go over strategies for - Forward vs backward mapping 2 1 The Limits of Geometric Modeling
MATH Lagrange multipliers in 3 variables Fall 2016
 MATH 20550 Lagrange multipliers in 3 variables Fall 2016 1. The one constraint they The problem is to find the extrema of a function f(x, y, z) subject to the constraint g(x, y, z) = c. The book gives
MATH 20550 Lagrange multipliers in 3 variables Fall 2016 1. The one constraint they The problem is to find the extrema of a function f(x, y, z) subject to the constraint g(x, y, z) = c. The book gives
Lecture IV Bézier Curves
 Lecture IV Bézier Curves Why Curves? Why Curves? Why Curves? Why Curves? Why Curves? Linear (flat) Curved Easier More pieces Looks ugly Complicated Fewer pieces Looks smooth What is a curve? Intuitively:
Lecture IV Bézier Curves Why Curves? Why Curves? Why Curves? Why Curves? Why Curves? Linear (flat) Curved Easier More pieces Looks ugly Complicated Fewer pieces Looks smooth What is a curve? Intuitively:
SPM Add Math Form 5 Chapter 3 Integration
 SPM Add Math Form Chapter Integration INDEFINITE INTEGRAL CHAPTER : INTEGRATION Integration as the reverse process of differentiation ) y if dy = x. Given that d Integral of ax n x + c = x, where c is
SPM Add Math Form Chapter Integration INDEFINITE INTEGRAL CHAPTER : INTEGRATION Integration as the reverse process of differentiation ) y if dy = x. Given that d Integral of ax n x + c = x, where c is
Three Dimensional Geometry. Linear Programming
 Three Dimensional Geometry Linear Programming A plane is determined uniquely if any one of the following is known: The normal to the plane and its distance from the origin is given, i.e. equation of a
Three Dimensional Geometry Linear Programming A plane is determined uniquely if any one of the following is known: The normal to the plane and its distance from the origin is given, i.e. equation of a
Describe Plane Shapes
 Lesson 12.1 Describe Plane Shapes You can use math words to describe plane shapes. point an exact position or location line endpoints line segment ray a straight path that goes in two directions without
Lesson 12.1 Describe Plane Shapes You can use math words to describe plane shapes. point an exact position or location line endpoints line segment ray a straight path that goes in two directions without
Systems of Equations and Inequalities. Copyright Cengage Learning. All rights reserved.
 5 Systems of Equations and Inequalities Copyright Cengage Learning. All rights reserved. 5.5 Systems of Inequalities Copyright Cengage Learning. All rights reserved. Objectives Graphing an Inequality Systems
5 Systems of Equations and Inequalities Copyright Cengage Learning. All rights reserved. 5.5 Systems of Inequalities Copyright Cengage Learning. All rights reserved. Objectives Graphing an Inequality Systems
CSE 167: Introduction to Computer Graphics Lecture #10: View Frustum Culling
 CSE 167: Introduction to Computer Graphics Lecture #10: View Frustum Culling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2015 Announcements Project 4 due tomorrow Project
CSE 167: Introduction to Computer Graphics Lecture #10: View Frustum Culling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2015 Announcements Project 4 due tomorrow Project
Triangle meshes I. CS 4620 Lecture 2
 Triangle meshes I CS 4620 Lecture 2 2014 Steve Marschner 1 spheres Andrzej Barabasz approximate sphere Rineau & Yvinec CGAL manual 2014 Steve Marschner 2 finite element analysis PATRIOT Engineering 2014
Triangle meshes I CS 4620 Lecture 2 2014 Steve Marschner 1 spheres Andrzej Barabasz approximate sphere Rineau & Yvinec CGAL manual 2014 Steve Marschner 2 finite element analysis PATRIOT Engineering 2014
Surfaces and Partial Derivatives
 Surfaces and Partial Derivatives James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 9, 2016 Outline Partial Derivatives Tangent Planes
Surfaces and Partial Derivatives James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 9, 2016 Outline Partial Derivatives Tangent Planes
Mathematical Analysis of Tetrahedron (solid angle subtended by any tetrahedron at its vertex)
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter March 29, 2015 Mathematical Analysis of Tetrahedron solid angle subtended by any tetrahedron at its vertex) Harish Chandra Rajpoot Rajpoot,
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter March 29, 2015 Mathematical Analysis of Tetrahedron solid angle subtended by any tetrahedron at its vertex) Harish Chandra Rajpoot Rajpoot,
In what follows, we will focus on Voronoi diagrams in Euclidean space. Later, we will generalize to other distance spaces.
 Voronoi Diagrams 4 A city builds a set of post offices, and now needs to determine which houses will be served by which office. It would be wasteful for a postman to go out of their way to make a delivery
Voronoi Diagrams 4 A city builds a set of post offices, and now needs to determine which houses will be served by which office. It would be wasteful for a postman to go out of their way to make a delivery
[Anton, pp , pp ] & [Bourne, pp ]
![[Anton, pp , pp ] & [Bourne, pp ] [Anton, pp , pp ] & [Bourne, pp ]](/thumbs/85/91711765.jpg) hapter 3 Integral Theorems [Anton, pp. 1124 1130, pp. 1145 1160] & [Bourne, pp. 195 224] First of all some definitions which we will need in the following: Definition 3.1. (a) A domain (region) is an open
hapter 3 Integral Theorems [Anton, pp. 1124 1130, pp. 1145 1160] & [Bourne, pp. 195 224] First of all some definitions which we will need in the following: Definition 3.1. (a) A domain (region) is an open
Continuity and Tangent Lines for functions of two variables
 Continuity and Tangent Lines for functions of two variables James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 4, 2014 Outline 1 Continuity
Continuity and Tangent Lines for functions of two variables James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 4, 2014 Outline 1 Continuity
MATERIAL FOR A MASTERCLASS ON HYPERBOLIC GEOMETRY. Timeline. 10 minutes Exercise session: Introducing curved spaces
 MATERIAL FOR A MASTERCLASS ON HYPERBOLIC GEOMETRY Timeline 10 minutes Introduction and History 10 minutes Exercise session: Introducing curved spaces 5 minutes Talk: spherical lines and polygons 15 minutes
MATERIAL FOR A MASTERCLASS ON HYPERBOLIC GEOMETRY Timeline 10 minutes Introduction and History 10 minutes Exercise session: Introducing curved spaces 5 minutes Talk: spherical lines and polygons 15 minutes
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
The diagram above shows a sketch of the curve C with parametric equations
 1. The diagram above shows a sketch of the curve C with parametric equations x = 5t 4, y = t(9 t ) The curve C cuts the x-axis at the points A and B. (a) Find the x-coordinate at the point A and the x-coordinate
1. The diagram above shows a sketch of the curve C with parametric equations x = 5t 4, y = t(9 t ) The curve C cuts the x-axis at the points A and B. (a) Find the x-coordinate at the point A and the x-coordinate
3 Polygonal Modeling. Getting Started with Maya 103
 3 Polygonal Modeling In Maya, modeling refers to the process of creating virtual 3D surfaces for the characters and objects in the Maya scene. Surfaces play an important role in the overall Maya workflow
3 Polygonal Modeling In Maya, modeling refers to the process of creating virtual 3D surfaces for the characters and objects in the Maya scene. Surfaces play an important role in the overall Maya workflow
x 6 + λ 2 x 6 = for the curve y = 1 2 x3 gives f(1, 1 2 ) = λ actually has another solution besides λ = 1 2 = However, the equation λ
 Math 0 Prelim I Solutions Spring 010 1. Let f(x, y) = x3 y for (x, y) (0, 0). x 6 + y (4 pts) (a) Show that the cubic curves y = x 3 are level curves of the function f. Solution. Substituting y = x 3 in
Math 0 Prelim I Solutions Spring 010 1. Let f(x, y) = x3 y for (x, y) (0, 0). x 6 + y (4 pts) (a) Show that the cubic curves y = x 3 are level curves of the function f. Solution. Substituting y = x 3 in
Equation of tangent plane: for implicitly defined surfaces section 12.9
 Equation of tangent plane: for implicitly defined surfaces section 12.9 Some surfaces are defined implicitly, such as the sphere x 2 + y 2 + z 2 = 1. In general an implicitly defined surface has the equation
Equation of tangent plane: for implicitly defined surfaces section 12.9 Some surfaces are defined implicitly, such as the sphere x 2 + y 2 + z 2 = 1. In general an implicitly defined surface has the equation
Chapter 17: The Truth about Normals
 Chapter 17: The Truth about Normals What are Normals? When I first started with Blender I read about normals everywhere, but all I knew about them was: If there are weird black spots on your object, go
Chapter 17: The Truth about Normals What are Normals? When I first started with Blender I read about normals everywhere, but all I knew about them was: If there are weird black spots on your object, go
Chapter III.C Analysis of The Second Derivative Draft Version 4/19/14 Martin Flashman 2005
 Chapter III.C Analysis of The Second Derivative Draft Version 4/19/14 Martin Flashman 2005 In this section we will develop applications of the second derivative that explain more graphical features of
Chapter III.C Analysis of The Second Derivative Draft Version 4/19/14 Martin Flashman 2005 In this section we will develop applications of the second derivative that explain more graphical features of
4. TANGENTS AND NORMALS
 4. TANGENTS AND NORMALS 4. Equation of the Tangent at a Point Recall that the slope of a curve at a point is the slope of the tangent at that point. The slope of the tangent is the value of the derivative
4. TANGENTS AND NORMALS 4. Equation of the Tangent at a Point Recall that the slope of a curve at a point is the slope of the tangent at that point. The slope of the tangent is the value of the derivative
12.7 Tangent Planes and Normal Lines
 .7 Tangent Planes and Normal Lines Tangent Plane and Normal Line to a Surface Suppose we have a surface S generated by z f(x,y). We can represent it as f(x,y)-z 0 or F(x,y,z) 0 if we wish. Hence we can
.7 Tangent Planes and Normal Lines Tangent Plane and Normal Line to a Surface Suppose we have a surface S generated by z f(x,y). We can represent it as f(x,y)-z 0 or F(x,y,z) 0 if we wish. Hence we can
How do we draw a picture?
 1 How do we draw a picture? Define geometry. Now what? We can draw the edges of the faces. Wireframe. We can only draw the edges of faces that are visible. We can fill in the faces. Giving each object
1 How do we draw a picture? Define geometry. Now what? We can draw the edges of the faces. Wireframe. We can only draw the edges of faces that are visible. We can fill in the faces. Giving each object
Solved Examples. Parabola with vertex as origin and symmetrical about x-axis. We will find the area above the x-axis and double the area.
 Solved Examples Example 1: Find the area common to the curves x 2 + y 2 = 4x and y 2 = x. x 2 + y 2 = 4x (i) (x 2) 2 + y 2 = 4 This is a circle with centre at (2, 0) and radius 2. y = (4x-x 2 ) y 2 = x
Solved Examples Example 1: Find the area common to the curves x 2 + y 2 = 4x and y 2 = x. x 2 + y 2 = 4x (i) (x 2) 2 + y 2 = 4 This is a circle with centre at (2, 0) and radius 2. y = (4x-x 2 ) y 2 = x
Geometry Definitions and Theorems. Chapter 9. Definitions and Important Terms & Facts
 Geometry Definitions and Theorems Chapter 9 Definitions and Important Terms & Facts A circle is the set of points in a plane at a given distance from a given point in that plane. The given point is the
Geometry Definitions and Theorems Chapter 9 Definitions and Important Terms & Facts A circle is the set of points in a plane at a given distance from a given point in that plane. The given point is the
Chapter 6. Curves and Surfaces. 6.1 Graphs as Surfaces
 Chapter 6 Curves and Surfaces In Chapter 2 a plane is defined as the zero set of a linear function in R 3. It is expected a surface is the zero set of a differentiable function in R n. To motivate, graphs
Chapter 6 Curves and Surfaces In Chapter 2 a plane is defined as the zero set of a linear function in R 3. It is expected a surface is the zero set of a differentiable function in R n. To motivate, graphs
Triangle meshes I. CS 4620 Lecture Kavita Bala (with previous instructor Marschner) Cornell CS4620 Fall 2015 Lecture 2
 Triangle meshes I CS 4620 Lecture 2 1 Shape http://fc00.deviantart.net/fs70/f/2014/220/5/3/audi_r8_render_by_smiska333-d7u9pjt.jpg spheres Andrzej Barabasz approximate sphere Rineau & Yvinec CGAL manual
Triangle meshes I CS 4620 Lecture 2 1 Shape http://fc00.deviantart.net/fs70/f/2014/220/5/3/audi_r8_render_by_smiska333-d7u9pjt.jpg spheres Andrzej Barabasz approximate sphere Rineau & Yvinec CGAL manual
Section 2.1 Graphs. The Coordinate Plane
 Section 2.1 Graphs The Coordinate Plane Just as points on a line can be identified with real numbers to form the coordinate line, points in a plane can be identified with ordered pairs of numbers to form
Section 2.1 Graphs The Coordinate Plane Just as points on a line can be identified with real numbers to form the coordinate line, points in a plane can be identified with ordered pairs of numbers to form
A simple problem that has a solution that is far deeper than expected!
 The Water, Gas, Electricity Problem A simple problem that has a solution that is far deeper than expected! Consider the diagram below of three houses and three utilities: water, gas, and electricity. Each
The Water, Gas, Electricity Problem A simple problem that has a solution that is far deeper than expected! Consider the diagram below of three houses and three utilities: water, gas, and electricity. Each
Geometry Vocabulary. acute angle-an angle measuring less than 90 degrees
 Geometry Vocabulary acute angle-an angle measuring less than 90 degrees angle-the turn or bend between two intersecting lines, line segments, rays, or planes angle bisector-an angle bisector is a ray that
Geometry Vocabulary acute angle-an angle measuring less than 90 degrees angle-the turn or bend between two intersecting lines, line segments, rays, or planes angle bisector-an angle bisector is a ray that
An angle that has a measure less than a right angle.
 Unit 1 Study Strategies: Two-Dimensional Figures Lesson Vocab Word Definition Example Formed by two rays or line segments that have the same 1 Angle endpoint. The shared endpoint is called the vertex.
Unit 1 Study Strategies: Two-Dimensional Figures Lesson Vocab Word Definition Example Formed by two rays or line segments that have the same 1 Angle endpoint. The shared endpoint is called the vertex.
Triangle meshes I. CS 4620 Lecture Steve Marschner. Cornell CS4620 Spring 2017
 Triangle meshes I CS 4620 Lecture 2 2017 Steve Marschner 1 spheres Andrzej Barabasz approximate sphere Rineau & Yvinec CGAL manual 2017 Steve Marschner 2 finite element analysis PATRIOT Engineering 2017
Triangle meshes I CS 4620 Lecture 2 2017 Steve Marschner 1 spheres Andrzej Barabasz approximate sphere Rineau & Yvinec CGAL manual 2017 Steve Marschner 2 finite element analysis PATRIOT Engineering 2017
GEOMETRY IN THREE DIMENSIONS
 1 CHAPTER 5. GEOMETRY IN THREE DIMENSIONS 1 INSTITIÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW GEOMETRY IN THREE DIMENSIONS Contents 1 Geometry in R 3 2 1.1 Lines...............................................
1 CHAPTER 5. GEOMETRY IN THREE DIMENSIONS 1 INSTITIÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW GEOMETRY IN THREE DIMENSIONS Contents 1 Geometry in R 3 2 1.1 Lines...............................................
Day 5: Inscribing and Circumscribing Getting Closer to π: Inscribing and Circumscribing Polygons - Archimedes Method. Goals:
 Day 5: Inscribing and Circumscribing Getting Closer to π: Inscribing and Circumscribing Polygons - Archimedes Method Goals: Construct an inscribed hexagon and dodecagon. Construct a circumscribed hexagon
Day 5: Inscribing and Circumscribing Getting Closer to π: Inscribing and Circumscribing Polygons - Archimedes Method Goals: Construct an inscribed hexagon and dodecagon. Construct a circumscribed hexagon
Quiz 6 Practice Problems
 Quiz 6 Practice Problems Practice problems are similar, both in difficulty and in scope, to the type of problems you will see on the quiz. Problems marked with a are for your entertainment and are not
Quiz 6 Practice Problems Practice problems are similar, both in difficulty and in scope, to the type of problems you will see on the quiz. Problems marked with a are for your entertainment and are not
Lesson 3: Surface Creation
 Lesson 3: Surface Creation In this lesson, you will learn how to create surfaces from wireframes. Lesson Contents: Case Study: Surface Creation Design Intent Stages in the Process Choice of Surface Sweeping
Lesson 3: Surface Creation In this lesson, you will learn how to create surfaces from wireframes. Lesson Contents: Case Study: Surface Creation Design Intent Stages in the Process Choice of Surface Sweeping
1 Solution of Homework
 Math 3181 Dr. Franz Rothe February 2, 2012 All3181\4080_spr12h1.tex Name: Use the back pages for extra space due date: February 10 1 Solution of Homework Figure 1: A neutral construction of the tangents
Math 3181 Dr. Franz Rothe February 2, 2012 All3181\4080_spr12h1.tex Name: Use the back pages for extra space due date: February 10 1 Solution of Homework Figure 1: A neutral construction of the tangents
Core Mathematics 3 Functions
 http://kumarmaths.weebly.com/ Core Mathematics 3 Functions Core Maths 3 Functions Page 1 Functions C3 The specifications suggest that you should be able to do the following: Understand the definition of
http://kumarmaths.weebly.com/ Core Mathematics 3 Functions Core Maths 3 Functions Page 1 Functions C3 The specifications suggest that you should be able to do the following: Understand the definition of
03 - Reconstruction. Acknowledgements: Olga Sorkine-Hornung. CSCI-GA Geometric Modeling - Spring 17 - Daniele Panozzo
 3 - Reconstruction Acknowledgements: Olga Sorkine-Hornung Geometry Acquisition Pipeline Scanning: results in range images Registration: bring all range images to one coordinate system Stitching/ reconstruction:
3 - Reconstruction Acknowledgements: Olga Sorkine-Hornung Geometry Acquisition Pipeline Scanning: results in range images Registration: bring all range images to one coordinate system Stitching/ reconstruction:
CGT 581 G Geometric Modeling Curves
 CGT 581 G Geometric Modeling Curves Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Curves What is a curve? Mathematical definition 1) The continuous image of an interval
CGT 581 G Geometric Modeling Curves Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Curves What is a curve? Mathematical definition 1) The continuous image of an interval
Reflection & Mirrors
 Reflection & Mirrors Geometric Optics Using a Ray Approximation Light travels in a straight-line path in a homogeneous medium until it encounters a boundary between two different media A ray of light is
Reflection & Mirrors Geometric Optics Using a Ray Approximation Light travels in a straight-line path in a homogeneous medium until it encounters a boundary between two different media A ray of light is
Geometric Primitives. Chapter 5
 Chapter 5 Geometric Primitives In this chapter, we discuss the basic geometric primitives we will use to represent the world in which our graphic objects live. As discussed at the beginning of this class,
Chapter 5 Geometric Primitives In this chapter, we discuss the basic geometric primitives we will use to represent the world in which our graphic objects live. As discussed at the beginning of this class,
Mathematically, the path or the trajectory of a particle moving in space in described by a function of time.
 Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 45 : Curves in space [Section 45.1] Objectives In this section you will learn the following : Concept of curve in space. Parametrization
Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 45 : Curves in space [Section 45.1] Objectives In this section you will learn the following : Concept of curve in space. Parametrization
Glossary of dictionary terms in the AP geometry units
 Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
PAST QUESTIONS ON INTEGRATION PAPER 1
 PAST QUESTIONS ON INTEGRATION PAPER 1 1. Q9 Nov 2001 2. Q11 Nov 2001 3. The diagram shows the curve y = and the line y = x intersecting at O and P. Find the coordinates of P, [1] the area of the shaded
PAST QUESTIONS ON INTEGRATION PAPER 1 1. Q9 Nov 2001 2. Q11 Nov 2001 3. The diagram shows the curve y = and the line y = x intersecting at O and P. Find the coordinates of P, [1] the area of the shaded
CSCI 4620/8626. Coordinate Reference Frames
 CSCI 4620/8626 Computer Graphics Graphics Output Primitives Last update: 2014-02-03 Coordinate Reference Frames To describe a picture, the world-coordinate reference frame (2D or 3D) must be selected.
CSCI 4620/8626 Computer Graphics Graphics Output Primitives Last update: 2014-02-03 Coordinate Reference Frames To describe a picture, the world-coordinate reference frame (2D or 3D) must be selected.
Math (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines
 Math 18.02 (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines February 12 Reading Material: From Simmons: 17.1 and 17.2. Last time: Square Systems. Word problem. How many solutions?
Math 18.02 (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines February 12 Reading Material: From Simmons: 17.1 and 17.2. Last time: Square Systems. Word problem. How many solutions?
3. The three points (2, 4, 1), (1, 2, 2) and (5, 2, 2) determine a plane. Which of the following points is in that plane?
 Math 4 Practice Problems for Midterm. A unit vector that is perpendicular to both V =, 3, and W = 4,, is (a) V W (b) V W (c) 5 6 V W (d) 3 6 V W (e) 7 6 V W. In three dimensions, the graph of the equation
Math 4 Practice Problems for Midterm. A unit vector that is perpendicular to both V =, 3, and W = 4,, is (a) V W (b) V W (c) 5 6 V W (d) 3 6 V W (e) 7 6 V W. In three dimensions, the graph of the equation
Direction Fields; Euler s Method
 Direction Fields; Euler s Method It frequently happens that we cannot solve first order systems dy (, ) dx = f xy or corresponding initial value problems in terms of formulas. Remarkably, however, this
Direction Fields; Euler s Method It frequently happens that we cannot solve first order systems dy (, ) dx = f xy or corresponding initial value problems in terms of formulas. Remarkably, however, this
PARAMETRIC EQUATIONS AND POLAR COORDINATES
 10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES A coordinate system represents a point in the plane by an ordered pair of numbers called coordinates. PARAMETRIC EQUATIONS
10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES A coordinate system represents a point in the plane by an ordered pair of numbers called coordinates. PARAMETRIC EQUATIONS
REVIEW I MATH 254 Calculus IV. Exam I (Friday, April 29) will cover sections
 REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
Curvature Berkeley Math Circle January 08, 2013
 Curvature Berkeley Math Circle January 08, 2013 Linda Green linda@marinmathcircle.org Parts of this handout are taken from Geometry and the Imagination by John Conway, Peter Doyle, Jane Gilman, and Bill
Curvature Berkeley Math Circle January 08, 2013 Linda Green linda@marinmathcircle.org Parts of this handout are taken from Geometry and the Imagination by John Conway, Peter Doyle, Jane Gilman, and Bill
Optics II. Reflection and Mirrors
 Optics II Reflection and Mirrors Geometric Optics Using a Ray Approximation Light travels in a straight-line path in a homogeneous medium until it encounters a boundary between two different media The
Optics II Reflection and Mirrors Geometric Optics Using a Ray Approximation Light travels in a straight-line path in a homogeneous medium until it encounters a boundary between two different media The
12.5 Lines and Planes in 3D Lines: We use parametric equations for 3D lines. Here s a 2D warm-up:
 Closing Thu: 12.4(1)(2), 12.5(1) Closing next Tue: 12.5(2)(3), 12.6 Closing next Thu: 13.1, 13.2 12.5 Lines and Planes in 3D Lines: We use parametric equations for 3D lines. Here s a 2D warm-up: Consider
Closing Thu: 12.4(1)(2), 12.5(1) Closing next Tue: 12.5(2)(3), 12.6 Closing next Thu: 13.1, 13.2 12.5 Lines and Planes in 3D Lines: We use parametric equations for 3D lines. Here s a 2D warm-up: Consider
COMPUTING CONSTRAINED DELAUNAY
 COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE By Samuel Peterson, University of Minnesota Undergraduate The Goal The Problem The Algorithms The Implementation Applications Acknowledgments
COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE By Samuel Peterson, University of Minnesota Undergraduate The Goal The Problem The Algorithms The Implementation Applications Acknowledgments
Does a group of parallel line segments need to be the same length?
 1 Parallel Line Segments Parallel t Parallel What is the same about the groups of parallel line segments? They are always the same distance apart. They do not intersect each other. If you extend the line
1 Parallel Line Segments Parallel t Parallel What is the same about the groups of parallel line segments? They are always the same distance apart. They do not intersect each other. If you extend the line
AQA GCSE Further Maths Topic Areas
 AQA GCSE Further Maths Topic Areas This document covers all the specific areas of the AQA GCSE Further Maths course, your job is to review all the topic areas, answering the questions if you feel you need
AQA GCSE Further Maths Topic Areas This document covers all the specific areas of the AQA GCSE Further Maths course, your job is to review all the topic areas, answering the questions if you feel you need
11 cm. A rectangular container is 12 cm long, 11 cm wide and 10 cm high. The container is filled with water to a depth of 8 cm.
 Diagram NOT accurately drawn 10 cm 11 cm 12 cm 3.5 cm A rectangular container is 12 cm long, 11 cm wide and 10 cm high. The container is filled with water to a depth of 8 cm. A metal sphere of radius 3.5
Diagram NOT accurately drawn 10 cm 11 cm 12 cm 3.5 cm A rectangular container is 12 cm long, 11 cm wide and 10 cm high. The container is filled with water to a depth of 8 cm. A metal sphere of radius 3.5
Ray Tracing Basics I. Computer Graphics as Virtual Photography. camera (captures light) real scene. photo. Photographic print. Photography: processing
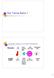 Ray Tracing Basics I Computer Graphics as Virtual Photography Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera model (focuses
Ray Tracing Basics I Computer Graphics as Virtual Photography Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera model (focuses
11/1/13. Visualization. Scientific Visualization. Types of Data. Height Field. Contour Curves. Meshes
 CSCI 420 Computer Graphics Lecture 26 Visualization Height Fields and Contours Scalar Fields Volume Rendering Vector Fields [Angel Ch. 2.11] Jernej Barbic University of Southern California Scientific Visualization
CSCI 420 Computer Graphics Lecture 26 Visualization Height Fields and Contours Scalar Fields Volume Rendering Vector Fields [Angel Ch. 2.11] Jernej Barbic University of Southern California Scientific Visualization
Visualization. CSCI 420 Computer Graphics Lecture 26
 CSCI 420 Computer Graphics Lecture 26 Visualization Height Fields and Contours Scalar Fields Volume Rendering Vector Fields [Angel Ch. 11] Jernej Barbic University of Southern California 1 Scientific Visualization
CSCI 420 Computer Graphics Lecture 26 Visualization Height Fields and Contours Scalar Fields Volume Rendering Vector Fields [Angel Ch. 11] Jernej Barbic University of Southern California 1 Scientific Visualization
For each question, indicate whether the statement is true or false by circling T or F, respectively.
 True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
Substituting a 2 b 2 for c 2 and using a little algebra, we can then derive the standard equation for an ellipse centred at the origin,
 Conics onic sections are the curves which result from the intersection of a plane with a cone. These curves were studied and revered by the ancient Greeks, and were written about extensively by both Euclid
Conics onic sections are the curves which result from the intersection of a plane with a cone. These curves were studied and revered by the ancient Greeks, and were written about extensively by both Euclid
Example: The following is an example of a polyhedron. Fill the blanks with the appropriate answer. Vertices:
 11.1: Space Figures and Cross Sections Polyhedron: solid that is bounded by polygons Faces: polygons that enclose a polyhedron Edge: line segment that faces meet and form Vertex: point or corner where
11.1: Space Figures and Cross Sections Polyhedron: solid that is bounded by polygons Faces: polygons that enclose a polyhedron Edge: line segment that faces meet and form Vertex: point or corner where
OpenGL Graphics System. 2D Graphics Primitives. Drawing 2D Graphics Primitives. 2D Graphics Primitives. Mathematical 2D Primitives.
 D Graphics Primitives Eye sees Displays - CRT/LCD Frame buffer - Addressable pixel array (D) Graphics processor s main function is to map application model (D) by projection on to D primitives: points,
D Graphics Primitives Eye sees Displays - CRT/LCD Frame buffer - Addressable pixel array (D) Graphics processor s main function is to map application model (D) by projection on to D primitives: points,
1) Find. a) b) c) d) e) 2) The function g is defined by the formula. Find the slope of the tangent line at x = 1. a) b) c) e) 3) Find.
 1 of 7 1) Find 2) The function g is defined by the formula Find the slope of the tangent line at x = 1. 3) Find 5 1 The limit does not exist. 4) The given function f has a removable discontinuity at x
1 of 7 1) Find 2) The function g is defined by the formula Find the slope of the tangent line at x = 1. 3) Find 5 1 The limit does not exist. 4) The given function f has a removable discontinuity at x
13.1. Functions of Several Variables. Introduction to Functions of Several Variables. Functions of Several Variables. Objectives. Example 1 Solution
 13 Functions of Several Variables 13.1 Introduction to Functions of Several Variables Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Objectives Understand
13 Functions of Several Variables 13.1 Introduction to Functions of Several Variables Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Objectives Understand
Tutte s Theorem: How to draw a graph
 Spectral Graph Theory Lecture 15 Tutte s Theorem: How to draw a graph Daniel A. Spielman October 22, 2018 15.1 Overview We prove Tutte s theorem [Tut63], which shows how to use spring embeddings to obtain
Spectral Graph Theory Lecture 15 Tutte s Theorem: How to draw a graph Daniel A. Spielman October 22, 2018 15.1 Overview We prove Tutte s theorem [Tut63], which shows how to use spring embeddings to obtain
 CHAPTER - 10 STRAIGHT LINES Slope or gradient of a line is defined as m = tan, ( 90 ), where is angle which the line makes with positive direction of x-axis measured in anticlockwise direction, 0 < 180
CHAPTER - 10 STRAIGHT LINES Slope or gradient of a line is defined as m = tan, ( 90 ), where is angle which the line makes with positive direction of x-axis measured in anticlockwise direction, 0 < 180
Topics and things to know about them:
 Practice Final CMSC 427 Distributed Tuesday, December 11, 2007 Review Session, Monday, December 17, 5:00pm, 4424 AV Williams Final: 10:30 AM Wednesday, December 19, 2007 General Guidelines: The final will
Practice Final CMSC 427 Distributed Tuesday, December 11, 2007 Review Session, Monday, December 17, 5:00pm, 4424 AV Williams Final: 10:30 AM Wednesday, December 19, 2007 General Guidelines: The final will
If the center of the sphere is the origin the the equation is. x y z 2ux 2vy 2wz d 0 -(2)
 Sphere Definition: A sphere is the locus of a point which remains at a constant distance from a fixed point. The fixed point is called the centre and the constant distance is the radius of the sphere.
Sphere Definition: A sphere is the locus of a point which remains at a constant distance from a fixed point. The fixed point is called the centre and the constant distance is the radius of the sphere.
Sec 4.1 Coordinates and Scatter Plots. Coordinate Plane: Formed by two real number lines that intersect at a right angle.
 Algebra I Chapter 4 Notes Name Sec 4.1 Coordinates and Scatter Plots Coordinate Plane: Formed by two real number lines that intersect at a right angle. X-axis: The horizontal axis Y-axis: The vertical
Algebra I Chapter 4 Notes Name Sec 4.1 Coordinates and Scatter Plots Coordinate Plane: Formed by two real number lines that intersect at a right angle. X-axis: The horizontal axis Y-axis: The vertical
Properties of Quadratic functions
 Name Today s Learning Goals: #1 How do we determine the axis of symmetry and vertex of a quadratic function? Properties of Quadratic functions Date 5-1 Properties of a Quadratic Function A quadratic equation
Name Today s Learning Goals: #1 How do we determine the axis of symmetry and vertex of a quadratic function? Properties of Quadratic functions Date 5-1 Properties of a Quadratic Function A quadratic equation
( ) ( 200, 0 ) and 0, 200. Linear programming 6C. ( 40, 0) and ( 0, 80) ( 100.8,16.8) F = 168. ( 37.5, 22.5) m=97.5. Objective line passes through
 Linear programming 6C 1 a Need intersection of 4x+y= 1400 and 3x+2y= 1200 ( 320,120) m=760 b ( 0, 400) N = 1600 c Need intersection of x+ 3y= 1200 and 3x+2y= 1200 ( 171 3, 342 6) 7 7 P= 514 2 7 d ( 350,
Linear programming 6C 1 a Need intersection of 4x+y= 1400 and 3x+2y= 1200 ( 320,120) m=760 b ( 0, 400) N = 1600 c Need intersection of x+ 3y= 1200 and 3x+2y= 1200 ( 171 3, 342 6) 7 7 P= 514 2 7 d ( 350,
Homework #2. Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves
 Computer Graphics Instructor: Brian Curless CSEP 557 Autumn 2016 Homework #2 Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves Assigned: Wednesday, Nov 16 th Due: Wednesday, Nov 30
Computer Graphics Instructor: Brian Curless CSEP 557 Autumn 2016 Homework #2 Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves Assigned: Wednesday, Nov 16 th Due: Wednesday, Nov 30
Scalar Field Visualization. Some slices used by Prof. Mike Bailey
 Scalar Field Visualization Some slices used by Prof. Mike Bailey Scalar Fields The approximation of certain scalar function in space f(x,y,z). Most of time, they come in as some scalar values defined on
Scalar Field Visualization Some slices used by Prof. Mike Bailey Scalar Fields The approximation of certain scalar function in space f(x,y,z). Most of time, they come in as some scalar values defined on
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot. Harish Chandra Rajpoot Rajpoot, HCR. Summer April 6, 2015
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Summer April 6, 2015 Mathematical Analysis of Uniform Polyhedron Trapezohedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Summer April 6, 2015 Mathematical Analysis of Uniform Polyhedron Trapezohedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices
True/False. MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY
 MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY True/False 10 points: points each) For the problems below, circle T if the answer is true and circle F is the answer is false. After you ve chosen
MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY True/False 10 points: points each) For the problems below, circle T if the answer is true and circle F is the answer is false. After you ve chosen
CONSTRUCTIONS Introduction Division of a Line Segment
 216 MATHEMATICS CONSTRUCTIONS 11 111 Introduction In Class IX, you have done certain constructions using a straight edge (ruler) and a compass, eg, bisecting an angle, drawing the perpendicular bisector
216 MATHEMATICS CONSTRUCTIONS 11 111 Introduction In Class IX, you have done certain constructions using a straight edge (ruler) and a compass, eg, bisecting an angle, drawing the perpendicular bisector
Calculation of the Focal Length of an Offset Satellite Dish Antenna
 Calculation of the Focal Length of an Offset Satellite Dish Antenna by John A R Legon, B.Sc. Given an offset satellite dish or antenna without LNB bracket or documentation, it is useful to be able to determine
Calculation of the Focal Length of an Offset Satellite Dish Antenna by John A R Legon, B.Sc. Given an offset satellite dish or antenna without LNB bracket or documentation, it is useful to be able to determine
