Greedy Algorithms. Interval Scheduling. Greedy Algorithms. Interval scheduling. Greedy Algorithms. Interval Scheduling
|
|
|
- Jack Evans
- 5 years ago
- Views:
Transcription
1 Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio without lookig to the future Wat the best curret partial solutio as if the curret step were the last step May be more tha oe greedy algorithm usig differet criteria to solve a give problem Greedy Algorithms Iterval Schedulig Greedy algorithms Easy to produce Fast ruig times Work oly o certai classes of problems Two methods for provig that greedy algorithms do work Greedy algorithm stays ahead At each step ay other algorithm will have a worse value for the criterio Exchage Argumet Ca trasform ay other solutio to the greedy solutio at o loss i quality Iterval Schedulig Sigle resource Reservatio requests Of form Ca I reserve it from start time s to fiish time f? s < f Fid: maximum umber of requests that ca be scheduled so that o two reservatios have the resource at the same time Iterval schedulig Greedy Algorithms for Iterval Schedulig Formally Requests,,, request i has start time s i ad fiish time f i > s i Requests i ad j are compatible iff either request i is for a time etirely before request j What criterio should we try? Earliest start time s i f i s j or, request j is for a time etirely before request i Shortest request time f i -s i f j s i Set A of requests is compatible iff every pair of requests i,j A, i j is compatible Goal: Fid maximum size subset A of compatible requests Earliest fiish fime f i
2 Greedy Algorithms for Iterval Schedulig What criterio should we try? Earliest start time s i Does t work Shortest request time f i -s i Does t work Eve fewest coflicts does t work Earliest fiish fime f i Works Greedy Algorithm for Iterval Schedulig R set of all requests A While R do Choose request i R with smallest fiishig time f i Add request i to A Delete all requests i R that are ot compatible with request i Retur A Greedy Algorithm for Iterval Schedulig Claim: A is a compatible set of requests ad these are added to A i order of fiish time Whe we add a request to A we delete all icompatible oes from R Claim: For ay other set O R of compatible requests the if we order requests i A ad O by fiish time the for each k: If O cotais a k th request the so does A ad the fiish time of the k th request i A, is the fiish time of the k th request i O, i.e. a k o k where a k ad o k are the respective fiish times Iductive Proof of Claim: a k o k Base Case: This is true for the first request i A sice that is the oe with the smallest fiish time Iductive Step: Suppose a k o k By defiitio of compatibility If O cotais a k+ st request r the the start time of that request must be after o k ad thus after a k Thus r is compatible with the first k requests i A Therefore A has at least k+ requests sice a compatible oe is available after the first k are chose r was amog those cosidered by the greedy algorithm for that k+ st request i A Therefore by the greedy choice the fiish time of r which is o k+ is at least the fiish time of that k+ st request i A which is a k+ Implemetig the Greedy Algorithm Exchage argumets Sort the requests by fiish time O(log ) time Maitai curret latest fiish time scheduled Keep array of start times idexed by request umber Oly elimiate icompatible requests as eeded Walk alog array of requests sorted by fiish times skippig those whose start time is before curret latest fiish time scheduled O() additioal time for greedy algorithm Schedulig to miimize lateess Sigle resource as i iterval schedulig but istead of start ad fiish times request i has Time requiremet t i which must be scheduled i a cotiguous block Target deadlie d i by which time the request would like to be fiished Overall start time s Requests are scheduled by the algorithm ito time itervals [s i,f i ] such that t i =f i -s i Lateess of schedule for request i is If d i <f i the request i is late by L i = f i -d i otherwise its lateess L i = Maximum lateess L=max i L i Goal: Fid a schedule for all requests (values of s i ad f i for each request i) to miimize the maximum lateess, L
3 Greedy Algorithm: Earliest Deadlie First Order requests i icreasig order of deadlies Schedule the request with the earliest deadlie as soo as the resource becomes available Greedy Algorithm: Earliest Deadlie First Sort deadlies i icreasig order (assume wlog that d d d ) f s for i to to s i f f i s i +t i f f i ed for Why does this give optimal value of maximum lateess? Easy observatios This schedule has o idle time The overall schedule starts at time s ad fiishes as soo as possible at time s+t +t + + t There is a optimal schedule with o idle time Shiftig the requests earlier by the amout of the idle time ca oly decrease maximum lateess (It might ot improve the maximum lateess but it certaily ca t hurt to do this.) There are oly a fiite # of schedules with o idle time so oe of them must be best Exchage Argumet We will show that if there is aother schedule O (thik optimal schedule) the we ca gradually chage O so that at each step the maximum lateess i O ever gets worse it evetually becomes the same as A Iversios Optimal schedules ad iversios Iversio d j < d i but i is scheduled before j Earliest deadlie first has o iversios Claim: All schedules with o iversios ad o idle time have the same maximum lateess Proof Schedules ca differ oly i how they order requests with equal deadlies Cosider all requests havig some commo deadlie d Maximum lateess of these jobs is based oly o the fiish time of the last of these jobs but the set of these requests occupy the same time segmet i both schedules Last of these requests fiishes at the same time i ay such schedule. Claim: There is a optimal schedule with o idle time ad o iversios Proof: By previous argumet there is a optimal schedule O with o idle time (i) If O has a iversio the it has a cosecutive pair of requests i its schedule that are iverted i.e. d j < d i but i is scheduled immediately before j (Simple trasitivity of <, otherwise cosecutive pairs would always be scheduled i icreasig order of deadlies)
4 Optimal schedules ad iversios Optimal schedules ad iversios (ii) If d j < d i but i is scheduled i O immediately before j the swappig requests i ad j to get schedule O does ot icrease the maximum lateess Lateess L j L j sice j is scheduled earlier i O tha i O Requests i ad j together occupy the same total time slot i both schedules All other requests k i have L k =L k (iii) Evetually these swaps will produce a optimal schedule with o iversios Each swap decreases the umber of iversios by There are at most (-)/ iversios QED f i =f j so L i = f j -d i < f j -d j =L j Maximum lateess has ot icreased! Earliest Deadlie First is optimal Optimal Cachig/Pagig We kow that There is a optimal schedule with o idle time or iversios All schedules with o idle time or iversios have the same maximum lateess EDF produces a schedule with o idle time or iversios Therefore EDF produces a optimal schedule Memory systems may levels of storage with differet access times smaller storage has shorter access time to access a item it must be brought to the lowest level of the memory system Cosider the maagemet problem betwee adjacet levels Mai memory with data items from a set U Cache ca hold k< items Simplest versio with o direct-mappig or other restrictios about where items ca be Suppose cache is full iitially Holds k data items to start with Optimal Cachig/Pagig Give a memory request d from U If d is stored i the cache we ca access it quickly If ot the we call it a cache miss ad (sice the cache is full) we must brig it ito cache ad evict some other data item from the cache which oe to evict? Give a sequece D=d,d,,d m of elemets from U correspodig to memory requests Fid a sequece of evictios (a evictio schedule) that has as few cache misses as possible Cachig Example =, k=, U={a,b,c} Cache iitially cotais {a,b} D= a b c b c a b S= a c C= a b a b c b This is optimal
5 A Note o Optimal Cachig I real operatig coditios oe typically eeds a o-lie algorithm make the evictio decisios as each memory request arrives However to desig ad aalyze these algorithms it is also importat to uderstad how the best possible decisios ca be made if oe did kow the future Field of o-lie algorithms compares the quality of o-lie decisios to that of the optimal schedule What does a optimal schedule look like? Belady s Greedy Algorithm: Farthest-I-Future Give sequece D=d,d,,d m Whe d i eeds to be brought ito the cache evict the item that is eeded farthest i the future Let NextAccess i (d)=mi{ j i : d j =d} be the ext poit i D that item d will be requested Evict d such that NextAccess i (d) is largest Other Algorithms Reduced Schedule Ofte there is flexibility, e.g. k=, C={a,b,c} D= a b c d a d e a d b c S FIF = c b e d S = b c d e Why are t other algorithms better? Least-Frequety-Used-I-Future? Exchage Argumet We ca swap choices to covert other schedules to Farthest-I-Future without losig quality We seemed to assume that we oly brought i ew items (ad evicted curret items) at cache misses Would actig i advace would help? Call a evictio schedule reduced if its oly evictios are of sigle items at cache misses Farthest-I-Future produces a reduced schedule Give a evictio schedule S defie schedule reduced(s) as follows: I step i if S brought i item d that is ot accessed util step j > i ad evicted item e from cache the preted to do this evictio leavig d i mai memory util step j Claim: reduced(s) yields at most as may cache misses as S does Optimal Cachig Fix some sequece D=d,d,,d m of requests Let S FIF be the schedule produced o this sequece by Farthest-I-Future Claim: If S is ay reduced schedule (for all of D) that agrees with S FIF for (at least) the first j steps the there is a reduced schedule S that agrees with S FIF for (at least) the first j+ steps such that #misses(s ) #misses(s) Applyig this claim m times we could start with ay optimal reduced schedule S (which agrees with S FIF for at least steps) ad produce S FIF without icreasig the umber of cache misses Provig the Claim Suppose S is a reduced schedule that agrees with S FIF for the first j steps At the time of the j+ st request d j+, S ad S FIF yield the same cache cotets Case : d j+ is i the cache Sice both S ad S FIF are reduced either has a miss so they agree for j+ steps ad we ca set S =S Case : d j+ is ot i the cache Say that S evicts f ad S FIF evicts e If e=f the we ca take S =S sice S ad S FIF agree for j+ steps What if e f?
6 Buildig S NextAccess j+ (e)>nextaccess j+ (f) Defie schedule S that agrees with S except that At step j+ it evicts e istead of f The first time after step j+ that oe of the followig occurs it does somethig differet that will result i S havig the same cache as S so that the rest of the simulatio ca take place Evet A: There is a request to a item g other tha e or f s.t. S evicts e Evet B: There is a request to f Note: S will have trouble hadlig ay access to e while it remais i the cache uder S but we wo t have to deal with it because Evet B will happe before ay access to e Buildig S Evet A: There is a request to a item g other tha e or f s.t. S evicts e I this case the cache uder S also does t cotai g (sice the caches uder S ad S ca at most disagree o e ad f) So we have S evict f Caches ow agree ad S is exactly the same as S for the rest #misses(s )=#misses(s). Buildig S Sigle-source shortest paths Evet B: There is a request to f Now f is i the cache uder S but ot S Say S evicts item e If e =e the after this step the caches uder S ad S are the same so we let S match S for the rest #misses(s )<#misses(s) If e e the have S evict e also ad brig i e istead Now cache uder S ad S agree ad S ca match S #misses(s )=#misses(s) But S is ot reduced so we replace S by reduce(s ) Reduce(S ) still agrees with S FIF for j+ steps Give a (u)directed graph G=(V,E) with each edge e havig a o-egative weight w(e) ad a vertex v Fid legth of shortest paths from v to each vertex i G A greedy algorithm Dijsktra s Algorithm : Maitai a set S of vertices whose shortest paths are kow iitially S={s} Maitaiig curret best legths of paths that oly go through S to each of the vertices i G path-legths to elemets of S will be right, to V-S they might ot be right Repeatedly add vertex v to S that has the shortest path-legth of ay vertex i V-S update path legths based o ew paths through v Dijkstra(G,w,s) S {s} d[s] while S V do of all edges e=(u,v) s.t. v S ad u S select* oe with the miimum value of d[u]+w(e) S S {v} d[v] d[u]+w(e) pred[v] u *For each v S maitai d [v]=miimum value of d[u]+w(e) over all vertices u S s.t. e=(u,v) is i of G
7 Update distaces Update distaces
8 Update distaces Update distaces Update distaces
9 Update distaces Update distaces Update distaces
10 Update distaces Update distaces Update distaces
11 Correctess Suppose all distaces to vertices i S are correct ad u has smallest curret value i V-S distace value of vertex i V-S=legth of shortest path from s with oly last edge leavig S s S x v Suppose some other path to v ad x= first vertex o this path ot i S d (v) d (x) x-v path legth other path is loger Therefore addig v to S keeps correct distaces Algorithm also produces a tree of shortest paths to v followig pred liks From w follow its acestors i the tree back to v If all you care about is the shortest path from v to w simply stop the algorithm whe w is added to S Implemetig Data Structure Review Need to keep curret distace values for odes i V-S fid miimum curret distace value reduce distaces whe vertex moved to S Priority Queue: Elemets each with a associated key Operatios Isert Fid-mi Retur the elemet with the smallest key Delete-mi Retur the elemet with the smallest key ad delete it from the data structure Decrease-key Decrease the key value of some elemet Implemetatios Arrays: O() time fid/delete-mi, O() time isert/ decrease-key Heaps: O(log ) time isert/decrease-key/delete-mi, O() time fid-mi with Priority Queues For each vertex u ot i tree maitai cost of curret cheapest path through tree to u Store u i priority queue with key = legth of this path Operatios: - isertios (each vertex added oce) - delete-mis (each vertex deleted oce) pick the vertex of smallest key, remove it from the priority queue ad add its edge to the graph <m decrease-keys (each edge updates oe vertex) Dijskstra s Algorithm with Priority Queues Priority queue implemetatios Array isert O(), delete-mi O(), decrease-key O() total O(+ +m)=o( ) Heap isert, delete-mi, decrease-key all O(log ) total O(m log ) d-heap (d=m/) isert, decrease-key O(log m/ ) delete-mi O((m/) log m/ ) total O(m log m/ )
12 Miimum Spaig Trees (Forests) Weighted Udirected Graph Give a udirected graph G=(V,E) with each edge e havig a weight w(e) Fid a subgraph T of G of miimum total weight s.t. every pair of vertices coected i G are also coected i T if G is coected the T is a tree otherwise it is a forest - First Greedy Algorithm Prim s Algorithm: start at a vertex s add the cheapest edge adjacet to s repeatedly add the cheapest edge that jois the vertices explored so far to the rest of the graph Exactly like Dijsktra s Algorithm but with a differet metric Dijsktra s Algorithm Dijkstra(G,w,s) S {s} d[s] while S V do of all edges e=(u,v) s.t. v S ad u S select* oe with the miimum value of d[u]+w(e) S S {v} d[v] d[u]+w(e) pred[v] u *For each v S maitai d [v]=miimum value of d[u]+w(e) over all vertices u S s.t. e=(u,v) is i of G Prim s Algorithm Prim(G,w,s) S {s} while S V do of all edges e=(u,v) s.t. v S ad u S select* oe with the miimum value of w(e) S S {v} pred[v] u *For each v S maitai small[v]=miimum value of w(e) over all vertices u S s.t. e=(u,v) is i of G Secod Greedy Algorithm Kruskal s Algorithm Start with the vertices ad o edges Repeatedly add the cheapest edge that jois two differet compoets. i.e. that does t create a cycle
13 Why greed is good Cuts ad Spaig Trees Defiitio: Give a graph G=(V,E), a cut of G is a partitio of V ito two o-empty pieces, S ad V-S Lemma: For every cut (S,V-S) of G, there is a miimum spaig tree (or forest) cotaiig ay cheapest edge crossig the cut, i.e. coectig some ode i S with some ode i V-S. call such a edge safe - The greedy algorithms always choose safe edges Prim s Algorithm Prim s Algorithm Always chooses cheapest edge from curret tree to rest of the graph This is cheapest edge across a cut which has the vertices of that tree o oe side. - The greedy algorithms always choose safe edges Kruskal s Algorithm Kruskal s Algorithm Always chooses cheapest edge coectig two pieces of the graph that are t yet coected This is the cheapest edge across ay cut which has those two pieces o differet sides ad does t split ay curret pieces. -
14 Kruskal s Algorithm Proof of Lemma: A Exchage Argumet - Suppose you have a MST ot usig cheapest edge e u e v Edpoits of e, u ad v must be coected i T Proof of Lemma Proof of Lemma Suppose you have a MST ot usig cheapest edge e Suppose you have a MST ot usig cheapest edge e u e v u e h v Edpoits of e, u ad v must be coected i T Edpoits of e, u ad v must be coected i T Proof of Lemma Proof of Lemma Suppose you have a MST ot usig cheapest edge e Replacig h by e does ot icrease weight of T w(e) w(h) w(e) w(h) u e h v u e h v Edpoits of e, u ad v must be coected i T All the same poits are coected by the ew tree
15 Kruskal s Algorithm Implemetatio & Aalysis First sort the edges by weight O(m log m) Go through edges from smallest to largest if edpoits of edge e are curretly i differet compoets the add to the graph else skip Uio-fid data structure hadles last part Total cost of last part: O(m α()) where α()<< log m Overall O(m log ) Uio-fid disjoit sets data structure Maitaiig compoets start with differet compoets oe per vertex fid compoets of the two edpoits of e m fids uio two compoets whe edge coectig them is added - uios Prim s Algorithm with Priority Queues For each vertex u ot i tree maitai curret cheapest edge from tree to u Store u i priority queue with key = weight of this edge Operatios: - isertios (each vertex added oce) - delete-mis (each vertex deleted oce) pick the vertex of smallest key, remove it from the p.q. ad add its edge to the graph <m decrease-keys (each edge updates oe vertex) Prim s Algorithm with Priority Queues Priority queue implemetatios Array isert O(), delete-mi O(), decrease-key O() total O(+ +m)=o( ) Heap isert, delete-mi, decrease-key all O(log ) total O(m log ) d-heap (d=m/) isert, decrease-key O(log m/ ) delete-mi O((m/) log m/ ) total O(m log m/ ) Boruvka s Algorithm () May other miimum spaig tree algorithms, most of them greedy A bit like Kruskal s Algorithm Start with compoets cosistig of a sigle vertex each At each step, each compoet chooses its cheapest outgoig edge to add to the spaig forest Two compoets may choose to add the same edge Useful for parallel algorithms sice compoets may be processed (almost) idepedetly Cherito & Tarja O(m loglog ) time usig a queue of compoets Chazelle O(m α(m) log α(m)) time Icredibly hairy algorithm Karger, Klei & Tarja O(m+) time radomized algorithm that works most of the time
16 Applicatios of Miimum Spaig Tree Algorithms Applicatios of Miimum Spaig Tree Algorithms Miimum cost etwork desig: Build a etwork to coect all locatios {v,,v } Cost of coectig v i to v j is w(v i,v j )> Choose a collectio of liks to create that will be as cheap as possible Ay miimum cost solutio is a MST If there is a solutio cotaiig a cycle the we ca remove ay edge ad get a cheaper solutio Maximum Spacig Clusterig Give a collectio U of objects {p,,p } Distace measure d(p i,p j ) satisfyig d(p i,p i )= d(p i,p j )> for i j d(p i,p j )=d(p j,p i ) Positive iteger k Fid a k-clusterig, i.e. partitio of U ito k clusters C,,C k, such that the spacig betwee the clusters is as large possible where spacig = mi{d(p i,p j ): p i ad p j i differet clusters} Greedy Algorithm Proof that this works Start with clusters each cosistig of a sigle poit Repeatedly fid the closest pair of poits i differet clusters uder distace d ad merge their clusters util oly k clusters remai Removig the k- most expesive edges from a MST yields k compoets C,,C k ad the spacig for them is precisely the cost d* of the k- st most expesive edge i the tree Gets the same compoets as Kruskal s Algorithm does! The sequece of closest pairs is exactly the MST Alteratively we could ru Kruskal s algorithm oce ad for ay k we could get the maximum spacig k-clusterig by deletig the k- most expesive edges Cosider ay other k-clusterig C,,C k Sice they are differet ad cover the same set of poits there is some pair of poits p i,p j such that p i,p j are i some cluster C r but p i, p j are i differet clusters C s ad C t Sice p i,p j C r, p i ad p j have a path betwee them all of whose edges have distace at most d* This path must cross betwee clusters i the C clusterig so the spacig i C is at most d*
CSE 521: Design and Analysis of Algorithms I
 CSE 521: Design and Analysis of Algorithms I Greedy Algorithms Paul Beame 1 Greedy Algorithms Hard to define exactly but can give general properties Solution is built in small steps Decisions on how to
CSE 521: Design and Analysis of Algorithms I Greedy Algorithms Paul Beame 1 Greedy Algorithms Hard to define exactly but can give general properties Solution is built in small steps Decisions on how to
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Minimum Spanning Trees
 Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Heaps. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
Priority Queues. Binary Heaps
 Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Sorting 9/15/2009. Sorting Problem. Insertion Sort: Soundness. Insertion Sort. Insertion Sort: Running Time. Insertion Sort: Soundness
 9/5/009 Algorithms Sortig 3- Sortig Sortig Problem The Sortig Problem Istace: A sequece of umbers Objective: A permutatio (reorderig) such that a ' K a' a, K,a a ', K, a' of the iput sequece The umbers
9/5/009 Algorithms Sortig 3- Sortig Sortig Problem The Sortig Problem Istace: A sequece of umbers Objective: A permutatio (reorderig) such that a ' K a' a, K,a a ', K, a' of the iput sequece The umbers
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Morgan Kaufmann Publishers 26 February, COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface. Chapter 5
 Morga Kaufma Publishers 26 February, 28 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Chapter 5 Set-Associative Cache Architecture Performace Summary Whe CPU performace icreases:
Morga Kaufma Publishers 26 February, 28 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Chapter 5 Set-Associative Cache Architecture Performace Summary Whe CPU performace icreases:
15-850: Advanced Algorithms CMU, Spring 2017 Lecture #2: Randomized MST and Directed MSTs January 27, 2017
 15-850: Advaced Algorithms CMU, Sprig 2017 Lecture #2: Radomized MST ad Directed MSTs Jauary 27, 2017 Lecturer: Aupam Gupta Scribe: Yu Zhao, Xiyu Wu 1 Prelimiaries I this lecture we itroduce the Karger-Klai-Tarja
15-850: Advaced Algorithms CMU, Sprig 2017 Lecture #2: Radomized MST ad Directed MSTs Jauary 27, 2017 Lecturer: Aupam Gupta Scribe: Yu Zhao, Xiyu Wu 1 Prelimiaries I this lecture we itroduce the Karger-Klai-Tarja
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
DATA STRUCTURES. amortized analysis binomial heaps Fibonacci heaps union-find. Data structures. Appetizer. Appetizer
 Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
CSE 417: Algorithms and Computational Complexity
 Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Basic allocator mechanisms The course that gives CMU its Zip! Memory Management II: Dynamic Storage Allocation Mar 6, 2000.
 5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
Computer Science Foundation Exam. August 12, Computer Science. Section 1A. No Calculators! KEY. Solutions and Grading Criteria.
 Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
Chapter 11. Friends, Overloaded Operators, and Arrays in Classes. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Chapter 9. Pointers and Dynamic Arrays. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Graphs ORD SFO LAX DFW
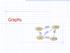 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Design and Analysis of Algorithms Notes
 Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
CS200: Hash Tables. Prichard Ch CS200 - Hash Tables 1
 CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Data Structures Week #9. Sorting
 Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Switching Hardware. Spring 2018 CS 438 Staff, University of Illinois 1
 Switchig Hardware Sprig 208 CS 438 Staff, Uiversity of Illiois Where are we? Uderstad Differet ways to move through a etwork (forwardig) Read sigs at each switch (datagram) Follow a kow path (virtual circuit)
Switchig Hardware Sprig 208 CS 438 Staff, Uiversity of Illiois Where are we? Uderstad Differet ways to move through a etwork (forwardig) Read sigs at each switch (datagram) Follow a kow path (virtual circuit)
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
Operating System Concepts. Operating System Concepts
 Chapter 4: Mass-Storage Systems Logical Disk Structure Logical Disk Structure Disk Schedulig Disk Maagemet RAID Structure Disk drives are addressed as large -dimesioal arrays of logical blocks, where the
Chapter 4: Mass-Storage Systems Logical Disk Structure Logical Disk Structure Disk Schedulig Disk Maagemet RAID Structure Disk drives are addressed as large -dimesioal arrays of logical blocks, where the
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
Administrative UNSUPERVISED LEARNING. Unsupervised learning. Supervised learning 11/25/13. Final project. No office hours today
 Admiistrative Fial project No office hours today UNSUPERVISED LEARNING David Kauchak CS 451 Fall 2013 Supervised learig Usupervised learig label label 1 label 3 model/ predictor label 4 label 5 Supervised
Admiistrative Fial project No office hours today UNSUPERVISED LEARNING David Kauchak CS 451 Fall 2013 Supervised learig Usupervised learig label label 1 label 3 model/ predictor label 4 label 5 Supervised
Chapter 24. Sorting. Objectives. 1. To study and analyze time efficiency of various sorting algorithms
 Chapter 4 Sortig 1 Objectives 1. o study ad aalyze time efficiecy of various sortig algorithms 4. 4.7.. o desig, implemet, ad aalyze bubble sort 4.. 3. o desig, implemet, ad aalyze merge sort 4.3. 4. o
Chapter 4 Sortig 1 Objectives 1. o study ad aalyze time efficiecy of various sortig algorithms 4. 4.7.. o desig, implemet, ad aalyze bubble sort 4.. 3. o desig, implemet, ad aalyze merge sort 4.3. 4. o
CS 111: Program Design I Lecture 21: Network Analysis. Robert H. Sloan & Richard Warner University of Illinois at Chicago April 10, 2018
 CS 111: Program Desig I Lecture 21: Network Aalysis Robert H. Sloa & Richard Warer Uiversity of Illiois at Chicago April 10, 2018 NETWORK ANALYSIS Which displays a graph i the sese of graph/etwork aalysis?
CS 111: Program Desig I Lecture 21: Network Aalysis Robert H. Sloa & Richard Warer Uiversity of Illiois at Chicago April 10, 2018 NETWORK ANALYSIS Which displays a graph i the sese of graph/etwork aalysis?
Computers and Scientific Thinking
 Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Data Structures Week #5. Trees (Ağaçlar)
 Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Minimum-Spanning-Tree problem. Minimum Spanning Trees (Forests) Minimum-Spanning-Tree problem
 Minimum Spanning Trees (Forests) Given an undirected graph G=(V,E) with each edge e having a weight w(e) : Find a subgraph T of G of minimum total weight s.t. every pair of vertices connected in G are
Minimum Spanning Trees (Forests) Given an undirected graph G=(V,E) with each edge e having a weight w(e) : Find a subgraph T of G of minimum total weight s.t. every pair of vertices connected in G are
Morgan Kaufmann Publishers 26 February, COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface. Chapter 5.
 Morga Kaufma Publishers 26 February, 208 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Chapter 5 Virtual Memory Review: The Memory Hierarchy Take advatage of the priciple
Morga Kaufma Publishers 26 February, 208 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Chapter 5 Virtual Memory Review: The Memory Hierarchy Take advatage of the priciple
Chapter 3 Classification of FFT Processor Algorithms
 Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Data Structures and Algorithms Part 1.4
 1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Copyright 2016 Ramez Elmasri and Shamkant B. Navathe
 Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 26 Ehaced Data Models: Itroductio to Active, Temporal, Spatial, Multimedia, ad Deductive Databases Copyright 2016 Ramez Elmasri ad Shamkat B.
Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 26 Ehaced Data Models: Itroductio to Active, Temporal, Spatial, Multimedia, ad Deductive Databases Copyright 2016 Ramez Elmasri ad Shamkat B.
Threads and Concurrency in Java: Part 1
 Cocurrecy Threads ad Cocurrecy i Java: Part 1 What every computer egieer eeds to kow about cocurrecy: Cocurrecy is to utraied programmers as matches are to small childre. It is all too easy to get bured.
Cocurrecy Threads ad Cocurrecy i Java: Part 1 What every computer egieer eeds to kow about cocurrecy: Cocurrecy is to utraied programmers as matches are to small childre. It is all too easy to get bured.
Major CSL Write your name and entry no on every sheet of the answer script. Time 2 Hrs Max Marks 70
 NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
Threads and Concurrency in Java: Part 1
 Threads ad Cocurrecy i Java: Part 1 1 Cocurrecy What every computer egieer eeds to kow about cocurrecy: Cocurrecy is to utraied programmers as matches are to small childre. It is all too easy to get bured.
Threads ad Cocurrecy i Java: Part 1 1 Cocurrecy What every computer egieer eeds to kow about cocurrecy: Cocurrecy is to utraied programmers as matches are to small childre. It is all too easy to get bured.
THE PROBLEM THE PROBLEM (1) THE PROBLEM (2) THE MINIMUM ENERGY BROADCAST PROBLEM THE MINIMUM SPANNING TREE
 THE MINIMUM ENERGY BROADCAST PROBLEM I.E. THE MINIMUM SPANNING TREE PROBLEM Prof. Tiziaa Calamoeri Network Algorithms A.y. 05/ THE PROBLEM THE PROBLEM () THE PROBLEM () What does it meas sufficietly close?!
THE MINIMUM ENERGY BROADCAST PROBLEM I.E. THE MINIMUM SPANNING TREE PROBLEM Prof. Tiziaa Calamoeri Network Algorithms A.y. 05/ THE PROBLEM THE PROBLEM () THE PROBLEM () What does it meas sufficietly close?!
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
CMSC Computer Architecture Lecture 10: Caches. Prof. Yanjing Li University of Chicago
 CMSC 22200 Computer Architecture Lecture 10: Caches Prof. Yajig Li Uiversity of Chicago Midterm Recap Overview ad fudametal cocepts ISA Uarch Datapath, cotrol Sigle cycle, multi cycle Pipeliig Basic idea,
CMSC 22200 Computer Architecture Lecture 10: Caches Prof. Yajig Li Uiversity of Chicago Midterm Recap Overview ad fudametal cocepts ISA Uarch Datapath, cotrol Sigle cycle, multi cycle Pipeliig Basic idea,
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Σ P(i) ( depth T (K i ) + 1),
 EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
quality/quantity peak time/ratio
 Semi-Heap ad Its Applicatios i Touramet Rakig Jie Wu Departmet of omputer Sciece ad Egieerig Florida Atlatic Uiversity oca Rato, FL 3343 jie@cse.fau.edu September, 00 . Itroductio ad Motivatio. relimiaries
Semi-Heap ad Its Applicatios i Touramet Rakig Jie Wu Departmet of omputer Sciece ad Egieerig Florida Atlatic Uiversity oca Rato, FL 3343 jie@cse.fau.edu September, 00 . Itroductio ad Motivatio. relimiaries
Chapter 1. Introduction to Computers and C++ Programming. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 1 Itroductio to Computers ad C++ Programmig Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 1.1 Computer Systems 1.2 Programmig ad Problem Solvig 1.3 Itroductio to C++ 1.4 Testig
Chapter 1 Itroductio to Computers ad C++ Programmig Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 1.1 Computer Systems 1.2 Programmig ad Problem Solvig 1.3 Itroductio to C++ 1.4 Testig
1. SWITCHING FUNDAMENTALS
 . SWITCING FUNDMENTLS Switchig is the provisio of a o-demad coectio betwee two ed poits. Two distict switchig techiques are employed i commuicatio etwors-- circuit switchig ad pacet switchig. Circuit switchig
. SWITCING FUNDMENTLS Switchig is the provisio of a o-demad coectio betwee two ed poits. Two distict switchig techiques are employed i commuicatio etwors-- circuit switchig ad pacet switchig. Circuit switchig
Copyright 2016 Ramez Elmasri and Shamkant B. Navathe
 Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
Elementary Educational Computer
 Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Spanning Maximal Planar Subgraphs of Random Graphs
 Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
How do we evaluate algorithms?
 F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
why study sorting? Sorting is a classic subject in computer science. There are three reasons for studying sorting algorithms.
 Chapter 5 Sortig IST311 - CIS65/506 Clevelad State Uiversity Prof. Victor Matos Adapted from: Itroductio to Java Programmig: Comprehesive Versio, Eighth Editio by Y. Daiel Liag why study sortig? Sortig
Chapter 5 Sortig IST311 - CIS65/506 Clevelad State Uiversity Prof. Victor Matos Adapted from: Itroductio to Java Programmig: Comprehesive Versio, Eighth Editio by Y. Daiel Liag why study sortig? Sortig
Lecture Notes 6 Introduction to algorithm analysis CSS 501 Data Structures and Object-Oriented Programming
 Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
CMSC Computer Architecture Lecture 12: Virtual Memory. Prof. Yanjing Li University of Chicago
 CMSC 22200 Computer Architecture Lecture 12: Virtual Memory Prof. Yajig Li Uiversity of Chicago A System with Physical Memory Oly Examples: most Cray machies early PCs Memory early all embedded systems
CMSC 22200 Computer Architecture Lecture 12: Virtual Memory Prof. Yajig Li Uiversity of Chicago A System with Physical Memory Oly Examples: most Cray machies early PCs Memory early all embedded systems
Lecture 28: Data Link Layer
 Automatic Repeat Request (ARQ) 2. Go ack N ARQ Although the Stop ad Wait ARQ is very simple, you ca easily show that it has very the low efficiecy. The low efficiecy comes from the fact that the trasmittig
Automatic Repeat Request (ARQ) 2. Go ack N ARQ Although the Stop ad Wait ARQ is very simple, you ca easily show that it has very the low efficiecy. The low efficiecy comes from the fact that the trasmittig
Image Segmentation EEE 508
 Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
CSCI 5090/7090- Machine Learning. Spring Mehdi Allahyari Georgia Southern University
 CSCI 5090/7090- Machie Learig Sprig 018 Mehdi Allahyari Georgia Souther Uiversity Clusterig (slides borrowed from Tom Mitchell, Maria Floria Balca, Ali Borji, Ke Che) 1 Clusterig, Iformal Goals Goal: Automatically
CSCI 5090/7090- Machie Learig Sprig 018 Mehdi Allahyari Georgia Souther Uiversity Clusterig (slides borrowed from Tom Mitchell, Maria Floria Balca, Ali Borji, Ke Che) 1 Clusterig, Iformal Goals Goal: Automatically
Numerical Methods Lecture 6 - Curve Fitting Techniques
 Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
An Efficient Algorithm for Graph Bisection of Triangularizations
 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface. Chapter 4. The Processor. Part A Datapath Design
 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Chapter The Processor Part A path Desig Itroductio CPU performace factors Istructio cout Determied by ISA ad compiler. CPI ad
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Chapter The Processor Part A path Desig Itroductio CPU performace factors Istructio cout Determied by ISA ad compiler. CPI ad
arxiv: v2 [cs.ds] 24 Mar 2018
![arxiv: v2 [cs.ds] 24 Mar 2018 arxiv: v2 [cs.ds] 24 Mar 2018](/thumbs/81/83887444.jpg) Similar Elemets ad Metric Labelig o Complete Graphs arxiv:1803.08037v [cs.ds] 4 Mar 018 Pedro F. Felzeszwalb Brow Uiversity Providece, RI, USA pff@brow.edu March 8, 018 We cosider a problem that ivolves
Similar Elemets ad Metric Labelig o Complete Graphs arxiv:1803.08037v [cs.ds] 4 Mar 018 Pedro F. Felzeszwalb Brow Uiversity Providece, RI, USA pff@brow.edu March 8, 018 We cosider a problem that ivolves
Running Time. Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Characterizing graphs of maximum principal ratio
 Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Linked Lists 11/16/18. Preliminaries. Java References. Objects and references. Self references. Linking self-referential nodes
 Prelimiaries Liked Lists public class StrageObject { Strig ame; StrageObject other; Arrays are ot always the optimal data structure: A array has fixed size eeds to be copied to expad its capacity Addig
Prelimiaries Liked Lists public class StrageObject { Strig ame; StrageObject other; Arrays are ot always the optimal data structure: A array has fixed size eeds to be copied to expad its capacity Addig
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Running Time ( 3.1) Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time ( 3.1) Aalysis of Algorithms Iput Algorithm Output A algorithm is a step- by- step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects.
Ruig Time ( 3.1) Aalysis of Algorithms Iput Algorithm Output A algorithm is a step- by- step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects.
Analysis of Algorithms
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Ruig Time Most algorithms trasform iput objects ito output objects. The
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Ruig Time Most algorithms trasform iput objects ito output objects. The
3. b. Present a combinatorial argument that for all positive integers n : : 2 n
 . b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
. b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
