n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
|
|
|
- Marybeth Osborne
- 5 years ago
- Views:
Transcription
1 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset without repletio ot with cocer for order so there are such subsets. Alteratively, let represet the umber of elemets i such a subset that were selected from A. The value of may vary from 0 to. There are such selectios of the elemets from A. Now select which elemets from B will ot be i the subset (the that remai will thus be i the subset). There are of selectig these so ways of selectig the subset ad ways overall. = 0 This must equal.. a. [10] Preset a combiatorial argumet that for all 1: = 3 = 0 Let A = {a, b, c} ad cosider all strigs of legth usig elemets of A. Sice there are three optios for each compoet of the strig, there are 3 such strigs. Alteratively, cosider first cosider the positios of ay c's i the strig. Let represet the umber of o-c's (i.e., a's ad b's) i the strig. Clearly could rage from 0 through. For a fixed value of, there are ways to choose the positios for the o-c's. The for each of the positios, there are two optios (i.e., a or b) for the character i the positio. The remaiig - positios must be occupied by c's. Thus there are ways to assig elemets to the positios with o-c's. The total is ad this must equal 3 = 0 b. [10] Preset a combiatorial argumet that for all oegative itegers p, s, ad satisfyig p + s p p + s = p s p + s p (Hit: Cosider choosig two subsets.)
2 Let a set A have elemets ad cosider how may ways there are to select disjoit subsets B ad C of A so that B has p elemets ad C has s elemets. First we could select the p elemets for B i ways ad the select the s elemets for C from the remaiig p p -p elemets of A~ B i s ways. Together this yields p such p s selectios. Alteratively, we could first select the p+s elemets for B C i p + s p + s ways ad the select the p elemets for B from B C i ways. There are thus p p+ s p + s p such selectios ad this must equal p p s. a. [10] Preset a combiatorial argumet that for all 1: = 1 = 1 (Note: The summatio begis with = 1.) Cosider the cardiality of the set of o-empty subsets of a set A of elemets. For each elemet of A, there are two optios: either be preset i a subset or ot. Thus there are total subsets but oe of these is empty so there are 1 oempty subsets of A. Alteratively, let idicate the cardiality of the subset. Sice we are coutig o-empty subsets, rages from 1 to. For a fixed value of, there are ways of selectig the subset elemets from the total elemets of A. Addig this to iclude all possible cases of, we obtai ad this must = 1 equal 1.
3 b. [10] Preset a combiatorial argumet that for all itegers ad satisfyig 3 = (Hit: Cosider three special elemets.) Cosider the umber of subsets of size of a set B of cardiality. Sice 3, we may select three elemets b, b b of B ad let C = B { b, b, }. Thus C has 1, 3 cardiality -3 ad B = C { b 1, b, b 3 }. We ow there are such subsets. Alteratively, to select elemets of B for a subset there are four optios: all come from C, -1 come from C ad the th is either b,, or, -come from C ad the -1st ad th are exactly two of b 1, b, or, or -3 come from C ad all of b, b, 1 ad b 3 are preset. For the first optio, there are possibilities sice all come from C. For the secod optio, there are 3 possibilities, sice -1 1 elemets are selected from C ad oe from the three of b,, or b. For the third optio, there are 3 possibilities, sice - elemets are selected from C ad oe from the three of b 1, or b is ot selected. Lastly, if -3 come from C ad b, 3 ~ 1 b3 all of b ad b are preset, the there are, b 1, 3 optios. The total is 3 + ad this must equal [10] Preset a combiatorial argumet that for all positive itegers m,, ad r, satisfyig r mi{ m, } : m+ = r m r =0 r. (Hit: Cosider selectig from two sets.) Let A ad B be disjoit sets of cardialities m ad, respectively. Let C = A B ad cosider the umber of subsets of C of cardiality r. Sice m+ C = A + B) = m+, there are r such subsets. Alteratively let be the umber of elemets i a subset that came from A. The value of ca rage from m 0 to r. For a fixed value of, there are ways to select the elemets from b 3 1 b b 3 1 b 3
4 A ad ways to select the remaiig r r elemets from B, thus r m+ total ways. This must equal =0 r r. 3. [10] Preset a combiatorial argumet that for all positive itegers : 3 = = 0. Cosider as a model strigs of legth usig the characters from the set { abc,,}. For each positios there are 3 optios so there are 3 such strigs. Alteratively, let represet the umber of positios i the strig ot occupied by a (i.e., thus, occupied by either b or c ). The value of ca vary betwee 0 ad. For a fixed umber of b s ad c s, there are ways to determie the positios to be occupied by the b s ad c s ad the choices (either b or c ) for each of these positios, for a total of possibilities. The remaiig positios must be occupied by a s. Summig over all possible values of. We have such = 0 strigs ad this must equal 3. Examiatio 1 Solutios CS [5] For 3, how may diagoals does a covex polygo with extreme poits have? (Cosider a covex polygo give by extreme poits < P, P, 1..., P > i couterclocwise order A diagoal is a lie segmet coectig two o-adjacet extreme poits.) P 3... P P1 P For each of the extreme poits there are -3 distict extreme poits that o-adjacet. This would yield ( 3) edpoits of the diagoals. Sice each diagoal has two edpoits, there are ( 3) diagoals of a covex polygo with extreme poits.. a. [10] Preset a combiatorial argumet that for all 1: ()! ( 1) ( 3) 3 1=!
5 Cosider the set of all partitios of a set of cardiality ito pairs. For the left side, begi with ay permutatio of the elemets. The first elemet o the permutatio is i some pair ad there are 1 choices for its pair-mate. Removig these two from the permutatio, the ext elemet permutatio is also i some pair ad there are 3 choices for its pair-mate. The process cotiues util there are just two elemets left i the permutatio, ad they form the last pair. This yields ( 1) ( 3) 3 1 differet such partitios. Now cosider the right had side. There are ()! differet permutatios of the of the elemets. Pair the first elemet with the secod, the third with the fourth, etc. This yields a partitio ito pairs. However, the order amog the pairs is irrelevat to the partitio ad thus for every array of pairs there are differet permutatios. Lastly, the order amog the pairs, is also irrelevat, so a set of pairs could be arraged i! differet orders. Thus the umber of partitios ito pairs that igores order withi ad amog pairs is ( )! ad this must equal ( 1) ( 3) 3 1.! b. [10] Preset a combiatorial argumet that for all oegative itegers ad satisfyig + = Let set A have cardiality ad b ad c be distict elemets ot cotaied i A. Cosider the subsets of A {} b { c} of cardiality. For the left had side, we recogize that A {} b {} c has cardiality +, so there are + such subsets. Alteratively, cosider that a subset wither has all elemets comig from A, exactly 1 elemets comig from A, or A, exactly elemets comig from A. If all elemets come from A, there are. If exactly 1 elemets come from A, there are ways to select those elemets ad the two choices, b or, 1 to complete the subset. If exactly elemets come from A, there are ways to select those elemets ad the both b ad must be selected to complete the subset. The total is + + ad this must 1 + equal. 3. Preset a combiatorial argumet that for all positive values of m,, ad r:
6 m+ = r r = 0 m r m+ Cosider distict sets A ad B of cardialities m ad, respectively. There are r subset of A B of size r. Alteratively, for ay such subset, there must be some r- elemets of A ad elemets of B for a value of betwee 0 ad r. For a fixed there m r are m such subsets ad thus overall. r r = 0 3. a. [10] Usig a combiatorial argumet, prove that for 1: 1 = 1 = 1 (Hit: Let A ad B be disjoit sets of cardiality. Cosider pairs <C, a> where C A B, C has cardiality, ad a C A.) Usig the otatio of the hit, first choose a ad the choose C ~ { a}. There are choices for a (sice # A = ) ad there remai -1 elemets i A B ~ { a}. Thus, 1 there are total choices. Alteratively, let = # ( A C). The value of ca 1 rage from 1 (sice a A C ) to. For a fixed, there are choices for A C, choices from that for a, ad choices for C B. The total is = 1 b. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Usig the same otatio as above, cosider choosig just a set C A B of cardiality, There are such choices. Alteratively, let be the umber of elemets i A C : ca rage from 0 to. For a fixed, there are ways of choosig A C, ad sice there are - elemets i B C there are elemets i B ~ C, ad hece ways of choosig them. Choosig B ~ C however is equivalet to choosig
7 B C ad thus there are ways to choose B C. The total is ad this = 0 must equal. 3. a. [10] Usig a combiatorial argumet, prove that for ad m : + m = m + + Let A ad B be disjoit sets of cardialities ad m, respectively. We see to determie how may subsets of two elemets there are i A B. Sice the + m cardiality of A B is + m, there are such subsets. Alteratively, we could obtai such a subset by selectig oe elemet from each of A ad B, by selectig both elemets from A, or by selectig both elemets from B. There are m + + m + ways of doig this ad, therefore = m + +. b. [10] Usig a combiatorial argumet, prove that for itegers m,, p 1: p p p p m ( + m) = = 0 Let A ad B be disjoit sets of cardialities ad m, respectively. We see to determie how may strigs of legth p there are cosistig of elemets of A B. Sice the cardiality of A B is + m, there are + m optios for each of p positios i the sequece, so there are ( + m) p such sequeces. Alteratively, let deote the umber of positios i the sequece occupied by elemets of A. The p value of varies from 0 to p. For a fixed value of, there are ways to select these positios ad the optios for each of the positios. For each of the p positios occupied by elemets of B, there are m optios, thus p p p p m for the fixed value of ad m p overall. This must equal = 0 ( + m) p. 3. a. [10] Usig a combiatorial argumet, prove that for ad m : + m = m + +
8 Cosider subsets of two elemets from the uio of disjoit subsets A ad B with + m cardialities ad m, respectively. Sice #( A B) = + m, there are subsets of size two. Alteratively, cosider that either oe elemet comes from each of A ad B, both from A, or both from B. These ca be doe i m,, ad ways, respectively, ad the total is m + +. We coclude that + m = m + + b. [10] Usig a combiatorial argumet, prove that for 1: 1 = = 1 (Hit: Let A be a set of cardiality. Cosider pairs <B, a> where B A ad a A ~ B.) Employig the otatio from the hit, ad cosiderig the left side of the equatio first, there are choices for a ad the 1 subsets from the remaiig 1 elemets. Alteratively, let be the umber of elemets i { a} B. The value of could rage from 1 through. For a fixed value of, there are ways to choose{ a} B, ad the choices from this for a (with the remaiig chose elemets formig B ). There are total ways of doig this ad this must = 1 equal a. [10] Usig a combiatorial argumet, prove that for 1 ad m : ( m 1) = m = 0 Cosider strigs of legth selected from the itegers { 1,,..., m} with repetitio allowed. For each of positios there are m choices, so there are m such strigs. Alteratively, let idicate the umber of copies of m i the strig. The value of varies from 0 to. For a fixed value of there are selectios for the placemet of the m s ad the ( m 1) choices for the itegers { 1,,..., m 1} i
9 each of the remaiig positios. Thus there are ( m 1) such strigs with copies of m, ad ( m 1) = 0 overall. This must equal m. b. [10] Usig a combiatorial argumet, prove that for 0 :!( )! =! Cosider permutatios of legth selected from the itegers { 1,,..., }. There are! such permutatios. Alteratively, let satisfy 0 ad for ay permutatio first select the positios to be occupied by { 1,,..., }. There are such selectios. Now permute the values { 1,,...,} - there are! such permutatios. Fially, permute the values { + 1, +,..., }, which ca be doe i ( )! ways, ad place them ito the positios of the permutatio otoccupied by the values from { 1,,..., }. Thus, there are!( )! such permutatios ad this must equal!.
3. b. Present a combinatorial argument that for all positive integers n : : 2 n
 . b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
. b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Area As A Limit & Sigma Notation
 Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Xiaozhou (Steve) Li, Atri Rudra, Ram Swaminathan. HP Laboratories HPL Keyword(s): graph coloring; hardness of approximation
 Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Recursive Procedures. How can you model the relationship between consecutive terms of a sequence?
 6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
Partitions of a Convex Polygon
 HAPTER 6 Partitios of a ovex Polygo 6 INTRODUTION I our survey we have come across some results o eumeratio of ocrossig cofiguratios o the set of vertices of a covex polygo, such as triagulatios ad trees
HAPTER 6 Partitios of a ovex Polygo 6 INTRODUTION I our survey we have come across some results o eumeratio of ocrossig cofiguratios o the set of vertices of a covex polygo, such as triagulatios ad trees
UNIT 1 RECURRENCE RELATIONS
 UNIT RECURRENCE RELATIONS Structure Page No.. Itroductio 7. Objectives 7. Three Recurret Problems 8.3 More Recurreces.4 Defiitios 4.5 Divide ad Coquer 7.6 Summary 9.7 Solutios/Aswers. INTRODUCTION I the
UNIT RECURRENCE RELATIONS Structure Page No.. Itroductio 7. Objectives 7. Three Recurret Problems 8.3 More Recurreces.4 Defiitios 4.5 Divide ad Coquer 7.6 Summary 9.7 Solutios/Aswers. INTRODUCTION I the
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
Greedy Algorithms. Interval Scheduling. Greedy Algorithms. Interval scheduling. Greedy Algorithms. Interval Scheduling
 Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 2 (2013), No. 1, 5-22 INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES NENAD U. STOJANOVIĆ Abstract. If above each side of a regular polygo
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 2 (2013), No. 1, 5-22 INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES NENAD U. STOJANOVIĆ Abstract. If above each side of a regular polygo
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Counting II 3, 7 3, 2 3, 9 7, 2 7, 9 2, 9
 Coutig II Sometimes we will wat to choose objects from a set of objects, ad we wo t be iterested i orderig them For example, if you are leavig for vacatio ad you wat to pac your suitcase with three of
Coutig II Sometimes we will wat to choose objects from a set of objects, ad we wo t be iterested i orderig them For example, if you are leavig for vacatio ad you wat to pac your suitcase with three of
Design and Analysis of Algorithms Notes
 Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
The digraph drop polynomial
 The digraph drop polyomial Fa Chug Ro Graham Abstract For a weighted directed graph (or digraph, for short), deoted by D = (V, E, w), we defie a two-variable polyomial B D (x, y), called the drop polyomial
The digraph drop polyomial Fa Chug Ro Graham Abstract For a weighted directed graph (or digraph, for short), deoted by D = (V, E, w), we defie a two-variable polyomial B D (x, y), called the drop polyomial
IMP: Superposer Integrated Morphometrics Package Superposition Tool
 IMP: Superposer Itegrated Morphometrics Package Superpositio Tool Programmig by: David Lieber ( 03) Caisius College 200 Mai St. Buffalo, NY 4208 Cocept by: H. David Sheets, Dept. of Physics, Caisius College
IMP: Superposer Itegrated Morphometrics Package Superpositio Tool Programmig by: David Lieber ( 03) Caisius College 200 Mai St. Buffalo, NY 4208 Cocept by: H. David Sheets, Dept. of Physics, Caisius College
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
CS Polygon Scan Conversion. Slide 1
 CS 112 - Polygo Sca Coversio Slide 1 Polygo Classificatio Covex All iterior agles are less tha 180 degrees Cocave Iterior agles ca be greater tha 180 degrees Degeerate polygos If all vertices are colliear
CS 112 - Polygo Sca Coversio Slide 1 Polygo Classificatio Covex All iterior agles are less tha 180 degrees Cocave Iterior agles ca be greater tha 180 degrees Degeerate polygos If all vertices are colliear
The Magma Database file formats
 The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
State-space feedback 6 challenges of pole placement
 State-space feedbac 6 challeges of pole placemet J Rossiter Itroductio The earlier videos itroduced the cocept of state feedbac ad demostrated that it moves the poles. x u x Kx Bu It was show that whe
State-space feedbac 6 challeges of pole placemet J Rossiter Itroductio The earlier videos itroduced the cocept of state feedbac ad demostrated that it moves the poles. x u x Kx Bu It was show that whe
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Chapter 24. Sorting. Objectives. 1. To study and analyze time efficiency of various sorting algorithms
 Chapter 4 Sortig 1 Objectives 1. o study ad aalyze time efficiecy of various sortig algorithms 4. 4.7.. o desig, implemet, ad aalyze bubble sort 4.. 3. o desig, implemet, ad aalyze merge sort 4.3. 4. o
Chapter 4 Sortig 1 Objectives 1. o study ad aalyze time efficiecy of various sortig algorithms 4. 4.7.. o desig, implemet, ad aalyze bubble sort 4.. 3. o desig, implemet, ad aalyze merge sort 4.3. 4. o
Arithmetic Sequences
 . Arithmetic Sequeces COMMON CORE Learig Stadards HSF-IF.A. HSF-BF.A.1a HSF-BF.A. HSF-LE.A. Essetial Questio How ca you use a arithmetic sequece to describe a patter? A arithmetic sequece is a ordered
. Arithmetic Sequeces COMMON CORE Learig Stadards HSF-IF.A. HSF-BF.A.1a HSF-BF.A. HSF-LE.A. Essetial Questio How ca you use a arithmetic sequece to describe a patter? A arithmetic sequece is a ordered
Lower Bounds for Sorting
 Liear Sortig Topics Covered: Lower Bouds for Sortig Coutig Sort Radix Sort Bucket Sort Lower Bouds for Sortig Compariso vs. o-compariso sortig Decisio tree model Worst case lower boud Compariso Sortig
Liear Sortig Topics Covered: Lower Bouds for Sortig Coutig Sort Radix Sort Bucket Sort Lower Bouds for Sortig Compariso vs. o-compariso sortig Decisio tree model Worst case lower boud Compariso Sortig
The number n of subintervals times the length h of subintervals gives length of interval (b-a).
 Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
The Platonic solids The five regular polyhedra
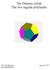 The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
CMPT 125 Assignment 2 Solutions
 CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
Algorithm Design Techniques. Divide and conquer Problem
 Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
On Alliance Partitions and Bisection Width for Planar Graphs
 Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
BOOLEAN MATHEMATICS: GENERAL THEORY
 CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
Parametric curves. Reading. Parametric polynomial curves. Mathematical curve representation. Brian Curless CSE 457 Spring 2015
 Readig Required: Agel 0.-0.3, 0.5., 0.6-0.7, 0.9 Parametric curves Bria Curless CSE 457 Sprig 05 Optioal Bartels, Beatty, ad Barsy. A Itroductio to Splies for use i Computer Graphics ad Geometric Modelig,
Readig Required: Agel 0.-0.3, 0.5., 0.6-0.7, 0.9 Parametric curves Bria Curless CSE 457 Sprig 05 Optioal Bartels, Beatty, ad Barsy. A Itroductio to Splies for use i Computer Graphics ad Geometric Modelig,
Computer Science Foundation Exam. August 12, Computer Science. Section 1A. No Calculators! KEY. Solutions and Grading Criteria.
 Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
CS200: Hash Tables. Prichard Ch CS200 - Hash Tables 1
 CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
Computers and Scientific Thinking
 Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
A New Bit Wise Technique for 3-Partitioning Algorithm
 Special Issue of Iteratioal Joural of Computer Applicatios (0975 8887) o Optimizatio ad O-chip Commuicatio, No.1. Feb.2012, ww.ijcaolie.org A New Bit Wise Techique for 3-Partitioig Algorithm Rajumar Jai
Special Issue of Iteratioal Joural of Computer Applicatios (0975 8887) o Optimizatio ad O-chip Commuicatio, No.1. Feb.2012, ww.ijcaolie.org A New Bit Wise Techique for 3-Partitioig Algorithm Rajumar Jai
Analysis Metrics. Intro to Algorithm Analysis. Slides. 12. Alg Analysis. 12. Alg Analysis
 Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
Bezier curves. Figure 2 shows cubic Bezier curves for various control points. In a Bezier curve, only
 Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
Numerical Methods Lecture 6 - Curve Fitting Techniques
 Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Data Structures and Algorithms Part 1.4
 1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
Chapter 8. Strings and Vectors. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 8 Strigs ad Vectors Overview 8.1 A Array Type for Strigs 8.2 The Stadard strig Class 8.3 Vectors Slide 8-3 8.1 A Array Type for Strigs A Array Type for Strigs C-strigs ca be used to represet strigs
Chapter 8 Strigs ad Vectors Overview 8.1 A Array Type for Strigs 8.2 The Stadard strig Class 8.3 Vectors Slide 8-3 8.1 A Array Type for Strigs A Array Type for Strigs C-strigs ca be used to represet strigs
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Matrix Partitions of Split Graphs
 Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Chapter 3 Classification of FFT Processor Algorithms
 Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
CSC 220: Computer Organization Unit 11 Basic Computer Organization and Design
 College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
INTERSECTION CORDIAL LABELING OF GRAPHS
 INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
EE123 Digital Signal Processing
 Last Time EE Digital Sigal Processig Lecture 7 Block Covolutio, Overlap ad Add, FFT Discrete Fourier Trasform Properties of the Liear covolutio through circular Today Liear covolutio with Overlap ad add
Last Time EE Digital Sigal Processig Lecture 7 Block Covolutio, Overlap ad Add, FFT Discrete Fourier Trasform Properties of the Liear covolutio through circular Today Liear covolutio with Overlap ad add
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES
 3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
Morgan Kaufmann Publishers 26 February, COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface. Chapter 5
 Morga Kaufma Publishers 26 February, 28 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Chapter 5 Set-Associative Cache Architecture Performace Summary Whe CPU performace icreases:
Morga Kaufma Publishers 26 February, 28 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Chapter 5 Set-Associative Cache Architecture Performace Summary Whe CPU performace icreases:
Fast Fourier Transform (FFT) Algorithms
 Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
Math 10C Long Range Plans
 Math 10C Log Rage Plas Uits: Evaluatio: Homework, projects ad assigmets 10% Uit Tests. 70% Fial Examiatio.. 20% Ay Uit Test may be rewritte for a higher mark. If the retest mark is higher, that mark will
Math 10C Log Rage Plas Uits: Evaluatio: Homework, projects ad assigmets 10% Uit Tests. 70% Fial Examiatio.. 20% Ay Uit Test may be rewritte for a higher mark. If the retest mark is higher, that mark will
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Asymptotics of Pattern Avoidance in the Klazar Set Partition and Permutation-Tuple Settings Permutation Patterns 2017 Abstract
 Asymptotics of Patter Avoiace i the Klazar Set Partitio a Permutatio-Tuple Settigs Permutatio Patters 2017 Abstract Bejami Guby Departmet of Mathematics Harvar Uiversity Cambrige, Massachusetts, U.S.A.
Asymptotics of Patter Avoiace i the Klazar Set Partitio a Permutatio-Tuple Settigs Permutatio Patters 2017 Abstract Bejami Guby Departmet of Mathematics Harvar Uiversity Cambrige, Massachusetts, U.S.A.
PLEASURE TEST SERIES (XI) - 04 By O.P. Gupta (For stuffs on Math, click at theopgupta.com)
 wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
Elementary Educational Computer
 Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
Chapter 8. Strings and Vectors. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 8 Strigs ad Vectors Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 8.1 A Array Type for Strigs 8.2 The Stadard strig Class 8.3 Vectors Copyright 2015 Pearso Educatio, Ltd..
Chapter 8 Strigs ad Vectors Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 8.1 A Array Type for Strigs 8.2 The Stadard strig Class 8.3 Vectors Copyright 2015 Pearso Educatio, Ltd..
why study sorting? Sorting is a classic subject in computer science. There are three reasons for studying sorting algorithms.
 Chapter 5 Sortig IST311 - CIS65/506 Clevelad State Uiversity Prof. Victor Matos Adapted from: Itroductio to Java Programmig: Comprehesive Versio, Eighth Editio by Y. Daiel Liag why study sortig? Sortig
Chapter 5 Sortig IST311 - CIS65/506 Clevelad State Uiversity Prof. Victor Matos Adapted from: Itroductio to Java Programmig: Comprehesive Versio, Eighth Editio by Y. Daiel Liag why study sortig? Sortig
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
South Slave Divisional Education Council. Math 10C
 South Slave Divisioal Educatio Coucil Math 10C Curriculum Package February 2012 12 Strad: Measuremet Geeral Outcome: Develop spatial sese ad proportioal reasoig It is expected that studets will: 1. Solve
South Slave Divisioal Educatio Coucil Math 10C Curriculum Package February 2012 12 Strad: Measuremet Geeral Outcome: Develop spatial sese ad proportioal reasoig It is expected that studets will: 1. Solve
Massachusetts Institute of Technology Lecture : Theory of Parallel Systems Feb. 25, Lecture 6: List contraction, tree contraction, and
 Massachusetts Istitute of Techology Lecture.89: Theory of Parallel Systems Feb. 5, 997 Professor Charles E. Leiserso Scribe: Guag-Ie Cheg Lecture : List cotractio, tree cotractio, ad symmetry breakig Work-eciet
Massachusetts Istitute of Techology Lecture.89: Theory of Parallel Systems Feb. 5, 997 Professor Charles E. Leiserso Scribe: Guag-Ie Cheg Lecture : List cotractio, tree cotractio, ad symmetry breakig Work-eciet
Data Structures Week #9. Sorting
 Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
Solution printed. Do not start the test until instructed to do so! CS 2604 Data Structures Midterm Spring, Instructions:
 CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
Appendix A. Use of Operators in ARPS
 A Appedix A. Use of Operators i ARPS The methodology for solvig the equatios of hydrodyamics i either differetial or itegral form usig grid-poit techiques (fiite differece, fiite volume, fiite elemet)
A Appedix A. Use of Operators i ARPS The methodology for solvig the equatios of hydrodyamics i either differetial or itegral form usig grid-poit techiques (fiite differece, fiite volume, fiite elemet)
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
