Large Feedback Arc Sets, High Minimum Degree Subgraphs, and Long Cycles in Eulerian Digraphs
|
|
|
- Zoe Booth
- 6 years ago
- Views:
Transcription
1 Combiatorics, Probability ad Computig (013, c Cambridge Uiversity Press 013 doi: /s Large Feedback Arc Sets, High Miimum Degree Subgraphs, ad Log Cycles i Euleria Digraphs HAO HUANG 1,JIEMA, ASAF SHAPIRA 3, BENNY SUDAKOV 4 ad RAPHAEL YUSTER 5 1 Departmet of Mathematics, UCLA, Los Ageles, CA 90095, USA ( huaghao@math.ucla.edu Departmet of Mathematics, UCLA, Los Ageles, CA 90095, USA ( jiema@math.ucla.edu 3 School of Mathematics, Tel Aviv Uiversity, Tel Aviv 69978, Israel ( asafico@tau.ac.il 4 Departmet of Mathematics, ETH, 809 Zurich, Switzerlad ad Departmet of Mathematics, UCLA, Los Ageles, CA 90095, USA ( bsudakov@math.ucla.edu 5 Departmet of Mathematics, Uiversity of Haifa, Haifa 31905, Israel ( raphy@math.haifa.ac.il Received 1 February 01; revised 7 August 013; first published olie 1 September 013 A miimum feedback arc set of a directed graph G is a smallest set of arcs whose removal makes G acyclic. Its cardiality is deoted by β(g. We show that a simple Euleria digraph with vertices ad m arcs has β(g m / + m/, ad this boud is optimal for ifiitely may m,. Usig this result we prove that a simple Euleria digraph cotais a cycle of legth at most 6 /m, ad has a Euleria subgraph with miimum degree at least m /4 3. Both estimates are tight up to a costat factor. Fially, motivated by a cojecture of Bollobás ad Scott, we also show how to fid log cycles i Euleria digraphs. 010 Mathematics subject classificatio: Primary 05C0 Secodary 05C38 1. Itroductio Extremal problems related to the existece of various types of cycles i graphs are some of the most basic ad well-studied problems i graph theory. Somewhat surprisigly, Research supported by a UC Dissertatio Year Fellowship. Supported i part by ISF grat 4/11 ad a Marie Curie CIG grat Research supported i part by NSF grat DMS , by AFOSR MURI grat FA ad by a USA Israel BSF grat.
2 860 H. Huag, J. Ma, A. Shapira, B. Sudakov ad R. Yuster i may cases it turs out that problems that are very easy to solve i the settig of udirected graphs become much more challegig i the settig of digraphs. A prime example is the well-kow Caccetta Häggkvist cojecture [4] (see below for more details. I some other cases, a result that holds for udirected graphs might fail completely for geeral digraphs, ad so it is atural to fid families of digraphs for which the result still holds. Motivated by a cojecture of Bollobás ad Scott [3], we cosider i this paper extremal problems of the above two types. It is well kow that a udirected graph G with vertices ad m edges has a subgraph with miimum degree at least m/, ad so if m such a G also cotais a cycle of legth at least m/ + 1. It is atural to ask whether results of this type ca be exteded to digraphs. However, it turs out that these statemets are ofte trivially false eve for very dese geeral digraphs. For istace, a trasitive touramet does ot cotai ay cycle, ad its subgraphs always have zero miimum i-degree ad outdegree. Therefore, i order to obtai meaigful results as i the udirected case, it is ecessary to restrict to a smaller family of digraphs. A atural cadidate oe may cosider is the family of Euleria digraphs, i which the i-degree equals the out-degree at each vertex. I this paper we ivestigate several atural parameters of Euleria digraphs, ad study the coectios betwee them. I particular, the parameters we cosider are miimum feedback arc set, shortest cycle, logest cycle, ad largest miimum degree of ay subgraph. Throughout this paper, we always assume the Euleria digraph is simple, i.e., it has o multiple arcs or loops, but arcs i differet directios such as (u, v ad (v, u are allowed. For other stadard graph-theoretic termiology ivolved, the reader is referred to []. A feedback arc set of a digraph is a set of arcs whose removal makes the digraph acyclic. Give a digraph G, deote by β(g the miimum size of a feedback arc set. Computig β(g ad fidig a correspodig miimum feedback arc set is a fudametal problem i combiatorial optimizatio. It has applicatios i may other fields such as testig of electroic circuits ad efficiet deadlock resolutio (see, e.g., [8, 10]. However, computig β(g turs out to be difficult, ad it is NP-hard eve for touramets [1, 5]. Oe basic questio i this area is to boud β(g as a fuctio of other parameters of G, ad there are several papers (see, e.g., [6, 7, 11] studyig upper bouds for β(g of this form. However, much less is kow about lower bouds for β(g, perhaps because a geeral digraph could be very dese ad still have a small miimum feedback arc set. For example, a trasitive touramet has β(g = 0. Nevertheless, it is easy to see that ay Euleria digraph G with vertices ad m arcs has β(g m/, sice the arcs ca be decomposed ito a disjoit uio of cycles, each of legth at most, ad ay feedback arc set cotais at least oe arc from each cycle. I this paper we actually prove the followig much stroger lower boud for β(g, ad show that it is tight for a ifiite family of Euleria digraphs. Theorem 1.1. Every Euleria digraph G with vertices ad m arcs has β(g m / + m/. Furthermore,if m the there exists a Euleria digraph G with vertices ad m arcs with β(g =m / + m/.
3 Large Feedback Arc Sets ad Log Cycles i Euleria digraphs 861 As metioed earlier, may problems related to cycles i udirected graphs are much harder to solve i the settig of digraphs. Oe of the most famous problems of this type is the celebrated Caccetta Häggkvist cojecture [4]: every directed -vertex digraph with miimum out-degree at least r cotais a cycle with legth at most /r, which is ot completely solved eve whe restricted to Euleria digraphs (for more discussio, we direct the iterested reader to the surveys [9, 1]. I this paper we study the existece of short cycles i Euleria digraphs with a give order ad size. The girth g(g of a digraph G is defied as the legth of the shortest cycle i G. Combiig Theorem 1.1 ad a result of Fox, Keevash ad Sudakov [7] which coects β(g ad g(g for a geeral digraph G, we are able to obtai the followig corollary. Corollary 1.. Every Euleria digraph G with vertices ad m arcs has g(g 6 /m. We also poit out that the upper boud i Corollary 1. is tight up to a costat, sice the costructio of Theorem 1.1 also provides a example of Euleria digraphs with girth at least /m. A repeated applicatio of Corollary 1. gives a Euleria subgraph of the origial digraph G, whose arc set is a disjoit uio of Ω(m / cycles. Usig this fact we ca fid a Euleria subgraph of G with large miimum degree. Theorem 1.3. Every Euleria digraph G with vertices ad m arcs has a Euleria subgraph with miimum degree at least m /4 3. This boud is tight up to a costat for ifiitely may m,. I 1996, Bollobás ad Scott ([3], Cojecture 6 asked whether every Euleria digraph G with o-egative arc-weightig w cotais a cycle of weight at least cw(g/, where w(g is the total weight ad c is some absolute costat. For the uweighted case, i.e., w =1, this cojecture becomes: Is it true that every Euleria digraph with vertices ad m arcs cotais a cycle of legth at least cm/? Eve this special case is still wide ope after 15 years. A obvious cosequece of Theorem 1.3 is that every Euleria digraph cotais a cycle of legth at least 1 + m /4 3. This ca be slightly improved to 1 + m / 3 usig Theorem 1.1 ad the simple fact that ay digraph has a cycle of legth at least β(g/ (see Sectio 4. Whe the digraph is dese, i.e., m = c, our theorem provides a cycle of legth liear i, which partially verifies the Bollobás Scott cojecture i this rage. However, observe that whe m is small, i particular whe m = o( 3/, Theorem 1.3 becomes meaigless. Nevertheless, we ca always fid a log cycle of legth at least m/ + 1, as show by the followig propositio. 1 Propositio 1.4. Every Euleria digraph G with vertices ad m arcs has a cycle of legth at least 1+ m/. Together with Theorem 1.1 ad the fact that ay digraph 1 This propositio was also obtaied idepedetly by Jacques Verstraete.
4 86 H. Huag, J. Ma, A. Shapira, B. Sudakov ad R. Yuster has a cycle of legth at least β(g/, this implies that G has a cycle of legth at least 1 + max{m / 3, m/ }. The rest of this paper is orgaized as follows. I Sectio, we obtai our bouds for feedback arc sets by provig Theorem 1.1. Sectio 3 cotais the proofs of our results for the existece of short cycles, log cycles, ad subgraph with large miimum degree. The fial sectio cotais some cocludig remarks ad ope problems.. Feedback arc sets This sectio cotais the proofs of Theorem 1.1. Cosider some liear order of the vertex set of a Euleria digraph G =(V,E with vertices ad m arcs. Let v i be the ith vertex i this order. We say that v i is before v j if i<j.aarc(v i,v j isaforward arc if i<j,ad is a backward arc if i>j. Observe that every cycle cotais at least oe backward arc. Hece, β(g is precisely the miimum umber of backward arcs over all liear orderigs. We prove Theorem 1.1 by showig that ay liear order of V has at least as may backward arcs as the amout stated i the theorem. We first require the followig simple lemma. Here a cut is defied as a partitio of the vertices of a digraph ito two disjoit subsets. Lemma.1. I ay cut (A, V \ A of a Euleria digraph, the umber of arcs from A to V \ A equals the umber of arcs from V \ A to A. Proof. The sum of the out-degrees of the vertices of A equals the sum of the i-degrees of the vertices of A. Each arc with both edpoits i A cotributes oe uit to each of these sums. Hece, the umber of arcs with oly oe edpoit i A splits equally betwee arcs that go from A to V \ A ad arcs that go from V \ A to A. Proof of Theorem 1.1. First we costruct a ifiite family of Euleria digraphs that achieves the boud i Theorem 1.1. For ay positive itegers, m such that t := m/ is a iteger, we defie the Cayley digraph G(, m to have vertex set {0, 1,..., 1} ad arc set {(i, i + j :1 i, 1 j t}, where all additios are modulo. From the defiitio, it is easy to verify that G(, m is a Euleria digraph. Cosider a order of the vertex set such that vertex i is the ith vertex i this order. We observe that for t +1 i, vertex i has backward arcs (i, j, where 1 j t ( i ad there is o backward arc from vertex i for i t. Therefore, t ( t +1 β(g(, m t ( i = j = = m + m. i= t+1 Next we prove the boud for arbitrary Euleria digraph. Fix a Euleria digraph G with V = ad E = m. We claim that it suffices to oly cosider Euleria digraphs which are -cycle-free, i.e., betwee ay pair of vertices {i, j} there do ot exist arcs i two differet directios. Suppose there are k differet -cycles i G. By removig all of them, we delete exactly k arcs. Note that the resultig -cycle-free digraph G is still Euleria j=1
5 Large Feedback Arc Sets ad Log Cycles i Euleria digraphs 863 ad cotais m k arcs. Therefore if Theorem 1.1 is true for all -cycle-free Euleria digraphs, the β(g (m k + m k. Obviously, i ay liear order of V (G, exactly half of the k arcs deleted must be backward arcs. Therefore, β(g β(g (m k +k + m k ( m + k = + m k(m k + k k ( m + m k( + k k = m + m. The last iequality follows from the fact that m k (, sice m k couts the umber of pairs of vertices with oe arc betwee them. From ow o, we always assume that G is a -cycle-free Euleria digraph. I order to prove a lower boud o β(g, we fix a liear orderig v 1 <v < <v with the miimum umber, β(g, of backward arcs. It will be importat for the aalysis to cosider the legth of a arc (v i,v j, which is i j. Observe that the legth of ay arc is a iteger i {1,..., 1}. Moreover, we call a arc short if its legth is at most /. Otherwise, it is log. Partitio the arc set E ito two parts, S ad L, wheres cotais the short arcs ad L cotais the log arcs. For a vertex v i,lets i deote the umber of short arcs coectig v i with some v j where j>i. It is importat to ote that at this poit we claim othig regardig the directios of these arcs. Sice G is -cycle-free, s i i. As each short arc (v i,v j cotributes exactly oe to either s i or s j, we have that s i = S. We ow estimate the sum of the legths of the short arcs. Cosider some vertex v i. Sice G is -cycle-free, the s i short arcs coectig v i to vertices appearig after v i must have distict legths. Hece, the sum of their legths is at least s i = ( s i +1. Thus, deotig by w(s the sum of the legths of the short arcs, we have that ( si +1 w(s. (.1 Next we calculate the sum of the legths of the log arcs, which is deoted by w(l. There is at most oe log arc of legth 1. There are at most two arcs of legth, ad, more geerally, there are at most i arcs of legth i. Thus, if we deote by t i the umber of log arcs of legth i for i / +1 ad set t i =0 for i /, we have that t i i, ad w(l = i t i. (.
6 864 H. Huag, J. Ma, A. Shapira, B. Sudakov ad R. Yuster Obviously, t i + s i = L + S = m. Let A i = {v 1,...,v i } ad cosider the cuts C i =(A i,v \ A i fori =1,...,.Letc i deote the umber of arcs crossig C i (ad otice that c = 0. Sice a arc of legth x crosses precisely x of these cuts, we have that c i = w(s+w(l. (.3 Cosider a pair of cuts C i,c i+ / for i =1,..., /. If a arc crosses both C i ad C i+ / the its legth is at least / + 1. Hece, a short arc caot cross both of these cuts. Let y i deote the umber of log arcs that cross both of these cuts. By Lemma.1, c i / backward arcs cross C i ad c i+ / / backward arcs cross C i+ /, ad we have couted at most y i such arcs twice. It follows that the umber of backward arcs is at least 1 (c i + c i+ / y i. Averagig over all / such pairs of cuts, it follows that the umber of backward arcs is at least 1 / / ( 1 (c i + c i+ / y i. (.4 As each log arc of legth j crosses precisely j / pairs of cuts C i ad C i+ /,we have / y i = j / t j (j / =w(l L /. This, together with (.3 ad (.4, gives β(g 1 ( 1 (w(s+w(l (w(l L / / w(s w(l + L. (.5 / Note that whe =k is eve, the above iequality becomes w(s w(l β(g + L. Next we show that whe =k + 1 is odd, the same iequality still holds. To see this, first assume that w(s w(l. The, applyig iequality (.5, we have that for =k +1, β(g w(s w(l k + L w(s w(l + L. Next suppose that w(s <w(l. Istead of cosiderig the cuts C i ad C i+k,welookat the pair C i ad C i+k+1 for i =1,...,k. Moreover, deote by z i the umber of log arcs
7 Large Feedback Arc Sets ad Log Cycles i Euleria digraphs 865 that cross both of these cuts. By a argumet similar to that used earlier, the umber of backward arcs is at least 1 (c i + c i+k+1 z i for 1 i k, adc i /fori = k + 1. This provides k + 1 lower bouds for β(g, ad we will average over all of them. Sice each log arc of legth j crosses precisely j (k +1 pairs of cuts C i ad C i+k+1, we agai have that k z i = t j (j (k +1=w(L (k +1 L, j k+1 ad we have β(g 1 ( k k +1 1 ( 1 k +1 w(s w(l k + ( 1 (c i + c i+k+1 z i + c k+1 (w(s+w(l (w(l (k +1 L + L w(s w(l + L, whereweusethefactthatw(l >w(s. Usig our lower boud estimate (.1 for w(s ad the expressio (. for w(l, we obtai w(s w(l β(g + L 1 ( ( si +1 i t i + = 1 ( ( si +1 +( it i. t i (.6 Defie F(s 1,...,s ; t 1,...,t := ( si +1 +( it i. I order to fid a lower boud of β(g, we eed to solve the followig iteger optimizatio problem: F(m, := mi F(s 1,...,s ; t 1,...,t subject to s i i, t i i, s i + t i = m. Lemma. below provides a precise solutio to this optimizatio problem, which gives that F(m, =tm (t t/, where t = m/. Hece, if we assume that m = t k
8 866 H. Huag, J. Ma, A. Shapira, B. Sudakov ad R. Yuster with 0 k 1, the β(g 1 F(m, =tm t t = t + t = (t k tk t + t + t k = t(t k tk + ( k k = m + m. t t The last iequality is because 0 k 1, so 0 k/ < 1adk / k/. Note that equality is possible oly whe m is a multiple of. Lemma.. F(m, =tm (t t/, wheret = m/. Proof. The proof of this lemma cosists of several claims. We set a i = s i + t i. The 0 a i ( i, s i i, ad i a i = m, ad the objective fuctio becomes ( si +1 +( it i = 1 s i ( i 1/s i +( ia i. Sice s i is a iteger, this fuctio of s i is miimized whe s i = i if a i i, ad whe s i = a i if a i < i. Therefore, subject to i a i = m ad a i ( i, we wat to miimize F = ( ai +1 + (( i +1 +( i(a i ( i a i < i a i i = ( ai +1 + ( ( i ( ia i. (.7 a i < i a i i For coveiece, defie A = {i : a i < i}, adb = {i : a i i}. Claim 1. For ay i A, if we icrease a i by 1 the F icreases by a i + 1, ad if we decrease a i by 1 the F decreases by a i.forayj B, if we icrease (decrease a j by 1 the F icreases (decreases by j. ( Proof. Note that whe a i = i or a i = i 1, ai +1 =( iai ( i, therefore if ( we icrease a i by1forayi A, the cotributio of a i to F always icreases by ai ( + ai +1 = ai + 1. Whe we decrease a i by 1, F decreases by ( a i ( +1 ai = ai.itis also easy to see that for ay j B, if we icrease or decrease a j by 1, the cotributio of a j to F always icreases or decreases by j. Claim. F is miimized whe A = {1,...,l 1} ad B = {l,...,} for some iteger l. Proof. We prove Claim by cotradictio. Suppose this statemet is false. The F is miimized by some {a i } such that there exists i<j, i B ad j A. Now we decrease a i by 1 ad icrease a j by 1, which ca be doe sice a j < ( j. The by Claim 1,
9 Large Feedback Arc Sets ad Log Cycles i Euleria digraphs 867 F decreases by ( i (a j +1 (j 1 (a j +1=( j a j > 0 sice j A, which cotradicts the miimality of F. We have a i = m, which is fixed. The ext claim shows that i order to miimize F, we eed to take the variables whose idex is i B to be as large as possible, with at most oe exceptio. Claim 3. F is miimized whe A = {1,...,l 1} ad B = {l,...,} for some iteger l. Moreover, a i =( i foralli l +1. Proof. First ote that for i B, its cotributio to F is ( ia i ( i. The secod term is fixed, ad a i has coefficiet i which decreases i i. Therefore, whe F is miimized, if i is the largest idex i B such that a i < ( i, the all j<i i B must satisfy a j = j; otherwise we might decrease a j ad icrease a i to make F smaller. Therefore, if i>l, we have a i 1 = i + 1. Note that if we icrease a i by 1 ad decrease a i 1 by 1, by Claim 1 the target fuctio F decreases by a i 1 ( i = 1. Therefore the oly possibility is that i = l, which proves Claim 3. Claim 4. There is a extremal cofiguratio for which a i = l or a i = l +1 for i l 1, a l is betwee l ad ( l, ad a i =( i fori l +1. Proof. From Claim 3, we kow that i a extremal cofiguratio, a i < i for 1 i l 1, l a l ( l, ad a i =( i fori l + 1. Amog all extremal cofiguratios, we take oe with the largest l, ad for all such cofiguratios, we take oe for which a l is the smallest. For such a cofiguratio, if we icrease a j by1for some j A ad decrease a l by 1, the by Claim 1, F icreases by (a j +1 ( l, which must be o-egative. Suppose a j +1= l. Ifj is chaged to be i B, it cotradicts Claim 3 o matter whether l remais i B or is chaged to be i A; ifj remais i A, it cotradicts the maximality of l if l is chaged to be i A or cotradicts the miimality of a l if l remais i B. Therefore a j l for every 1 j l 1. We ext cosider two cases: either a l is equal to ( l, or strictly less tha ( l. Case 1: a l =( l. From the discussios above, we already kow that a j l for every 1 j l 1. I particular a l 1 = l, sice it is strictly less tha (l 1. If, for some j l 1, a j l +, the we ca decrease a j by 1 ad icrease a l 1 by 1, sice a j is strictly greater tha 0 ad a l 1 is strictly less tha ( l +1.ByClaim1,F decreases by a j ( l +1 1, which cotradicts the miimality of F. Hece we have that l a j l +1foreveryj l 1. Case : a l < ( l. If we decrease a j by 1 ad icrease a l by 1, F decreases by a j ( l by Claim 1. Therefore a j l by the miimality of F, ad hece a j = l for all 1 j l 1. I both cases, the extremal cofiguratio cosists of l or l + 1 for the first l 1 variables, a l is betwee l ad ( l, ad a i =( i fori l +1.
10 868 H. Huag, J. Ma, A. Shapira, B. Sudakov ad R. Yuster By Claim 4, we ca boud the umber of arcs m from both sides: l 1 m = a i + a i (l 1( l+( l+ ( i =( l( 1, l 1 m = a i + i=l a i < (l 1( l +1+ i=l i=l+1 ( i =( l +1( 1. Solvig these two iequalities, we get m l<+1 m 1 1. Let m = t k, wheret = m/ ad 0 k 1. It is ot difficult to check that if t k, l = t ad if t<k, l = t +1. Now let x be the umber of variables a 1,...,a l 1 which are equal to l + 1. Sice a i =( i fori l + 1, we have that x + a l = m (l 1( l a i = m ( ( l. (.8 Whe t k, the l = t ad i l+1 x + a l = m ( t =t k<t =( l, ad hece a l < ( l. By the aalysis of the secod case i Claim 4, a j = l = t for all j l 1, ad therefore x =0 ad a l =t k. Sice l = t, the usig the summatio formula k=1 k = k(k + 1(k +1/6, we have from (.7 that (with details of the calculatio omitted ( t +1 F = ( t 1 + t(t k = tm (t t/. i=l ( t + ( ( i i l+1 Now we assume t<k,adsol = t + 1. The, usig (.8 agai, ( i x + a l = m ( (t 1 = k +(t 1 > (t 1 = ( l. The oly possibility without cotradictig the secod case i Claim 4 is that a l =( l ad x = k. Thus there are k of a 1,...,a l 1 which are equal to l +1=t, ad the rest of k t are equal to t 1. Agai by (.7, ( ( t +1 t F = ( k+ (k t+ ( ( i ( i = tm (t t/. i l As we have covered both cases, we have completed the proof of Lemma.. 3. Short cycles, log cycles, ad Euleria subgraphs with high miimum degree I this sectio, we prove the existece of short cycles, log cycles, ad subgraphs with large miimum degree i Euleria digraphs. A importat compoet i our proofs is the
11 Large Feedback Arc Sets ad Log Cycles i Euleria digraphs 869 followig result by Fox, Keevash ad Sudakov [7] o geeral digraphs. We poit out that the origial Theorem 1. i [7] was proved with a costat 5, which ca be improved to 18 usig exactly the same proof if we further assume r 11. Theorem 3.1. If a digraph G o vertices has β(g > 18 /r, with r 11, theg cotais a cycle of legth at most r, i.e., g(g r. Applyig this theorem ad Theorem 1.1, we ca ow prove Corollary 1., which says that every Euleria digraph G with vertices ad m arcs cotais a cycle of legth at most 6 /m. Proof of Corollary 1.. Let r =6 /m. Give a Euleria digraph G with vertices ad m arcs, if G cotais a -cycle, the g(g 6 /m. So we may assume that G is -cycle-free ad thus m (. By Theorem 1.1, β(g m + m > m = 18 (6 /m. Sice r =6 /m > 6 / ( > 11, we ca use Theorem 3.1 to coclude that g(g r = 6 m. To see that this boud is tight up to a costat factor, we cosider the costructio of the Cayley digraphs i Theorem 1.1. It is ot hard to see that if k = m/, theshortest directed cycle i G(, m has legth at least /k /m. Next we show that every Euleria digraph with vertices ad m arcs has a Euleria subgraph with miimum degree Ω(m / 3. Proof of Theorem 1.3. We start with a Euleria digraph G with vertices ad m arcs. Note that Corollary 1. implies that every Euleria digraph with vertices ad at least m/ arcs cotais a cycle of legth at most 1 /m. I every step, we pick oe such cycle ad delete all of its arcs from G. Obviously the resultig digraph is still Euleria, ad this process will cotiue util there are less tha m/ arcs left i the digraph. Therefore through this process we obtai a collectio C of t arc-disjoit cycles C 1,...,C t,where t (m m//(1 /m m /4. Deote by H the uio of all these cycles, where obviously H is a Euleria subgraph of G. If H has miimum degree at least t/ m /4 3, the we are already doe. Otherwise, we repeatedly delete from H ay vertex v with degree d(v t/ 1, together with all the d(v cycles i C passig through v. This process stops after a fiite umber of steps. I the ed we delete at most ( t/ 1 t 1 cycles i C, so the resultig digraph H is o-empty. Moreover, every vertex i H has degree at least t/ m /4 3. Sice H is the disjoit uio of the remaiig cycles, it is also a Euleria subgraph of G, adwe coclude the proof of Theorem 1.3.
12 870 H. Huag, J. Ma, A. Shapira, B. Sudakov ad R. Yuster Figure 1. The Euleria digraph H(s, t with s = 3. Remark. The proof of Theorem 1.3 also shows that G cotais a Euleria subgraph with miimum degree Ω(m / 3 ad at least Ω(m arcs. To see that the boud i Theorem 1.3 is tight up to a costat, for ay itegers s, t > 0, we costruct a Euleria digraph H := H(s, t such that: V (H =(U 1 U s (V 1 V t, U i = V j = s for 1 i s, 1 j t, for ay 1 i t 1 ad vertices u V i, v V i+1,thearc(u, v E(H, for ay 1 i s ad every vertex u U i, there is a arc from u to the ith vertex i V 1, ad aother arc from the ith vertex i V t to u. It ca be verified that H(s, t is a Euleria digraph with (s + ts vertices ad s (t +1 arcs. Moreover, every cycle i H(s, t must pass through a vertex i U 1 U s, whose degree is exactly 1. Therefore ay Euleria subgraph of H(s, t has miimum degree at most 1. Next we defie the δ-blowup H(s, t, δ: for ay iteger δ>0, we replace every vertex i V (H(s, t with a idepedet set W i = δ, adeacharc(i, j E(H(s, t by a complete bipartite digraph with arcs directed from W i to W j. The blowup digraph H(s, t, δ is still Euleria, ad has = s(s + tδ vertices ad m = s (t +1δ arcs. Takig t =s, we have that for H(s, s, δ, m 3 = (s (s +1δ (s(s +sδ 3 = 1 ( + 1 δ 4 7 s 7 δ. Note that, similarly to the previous discussio o H(s, t, every cycle i the blowup H(s, s, δ cotais at least oe vertex with degree δ. Therefore, the miimum degree of ay Euleria subgraph of H(s, s, δ is at most δ 7 m 4. This implies that the boud i 3 Theorem 1.3 is tight up to a costat factor for ifiitely may m,. Before provig Propositio 1.4, let us recall the followig easy fact.
13 Large Feedback Arc Sets ad Log Cycles i Euleria digraphs 871 Propositio 3.. If a digraph G has miimum out-degree δ + (G, theg cotais a directed cycle of legth at least δ + (G+1. Proof. Let P = v 1 v v t be the logest directed path i G. The all the out-eighbours of v t must lie o this path, otherwise P will become loger. If i<t is miimal with (v t,v i E(G, the v i v t v i gives a cycle of legth at least d + (v t +1 δ + (G+1. This propositio, together with Theorem 1.3, shows that a Euleria digraph G with vertices ad m arcs cotais a cycle of legth at least 1 + m /4 3. As discussed i the Itroductio, this ca be slightly improved to 1 + m / 3, but these bouds become meaigless whe the umber of arcs m is small. However, we may use a differet approach to obtai a cycle of legth at least m/ +1. Proof of Propositio 1.4. To prove that ay Euleria digraph G with vertices ad m arcs has a cycle of legth at least m/ + 1, we use iductio o the umber of vertices. Note that the base case whe = is obvious, sice the oly Euleria digraph is the -cycle with m/ + 1 =. Suppose the statemet is true for 1. Cosider a Euleria digraph G with vertices ad m arcs. If its miimum degree δ + (G isatleast m/, by Propositio 3., G already cotais a cycle of legth at least 1 + m/. Therefore we ca assume that there exists a vertex v with m/ >d + (v :=t. AsG is Euleria, there exist t arc-disjoit cycles C 1,C,...,C t passig through v. If oe of these cycles has legth at least m/ + 1, the agai we are doe. Otherwise, C i m/ for all 1 i t. Now we delete from G the vertex v together with the arcs of the cycles C 1,...,C t. The resultig Euleria digraph has 1 vertices ad m arcs, where t m = m C i m t ( m/ m 1 1. By the iductive hypothesis, the ew digraph (therefore G has a cycle of legth at least 1+ ( m /( 1 1+ m 1 1 /( 1 1+ m/. 4. Cocludig remarks We ed with some remarks o the Bollobás Scott cojecture whose uweighted versio states that a Euleria digraph with vertices ad m arcs has a cycle of legth Ω(m/. The caoical proof for showig that a udirected graph with this may vertices ad edges has a cycle of legth m/ proceeds by first passig to a subgraph G with miimum degree at least m/ ad the applyig Propositio 3. to G. We ca the iterpret the secod statemet of Theorem 1.3 as statig that whe applied to Euleria digraphs, this approach ca oly produce cycles of legth O(m / 3. There is, however, aother way to show that a udirected graph has a cycle of legth m/ usig depth-first search (DFS. Recall that the DFS is a graph algorithm that visits
14 87 H. Huag, J. Ma, A. Shapira, B. Sudakov ad R. Yuster all the vertices of a (directed or udirected graph G as follows. It maitais three sets of vertices, lettig S be the set of vertices which we have completed explorig them, T be the set of uvisited vertices, ad U = V (G \ (S T, where the vertices of U are kept i a stack (a last-i first-out data structure. The DFS starts with S = U = ad T = V (G. While there is a vertex i V (G \ S, ifu is o-empty, let v be the last vertex that was added to U. Ifv has a eighbour u T, the algorithm iserts u ito U ad repeats this step. If v does ot have a eighbour i T the v is popped out from U ad is iserted ito S. IfU is empty, the algorithm chooses a arbitrary vertex from T ad pushes it to U. Observe crucially that all the vertices i U form a directed path, ad that there are o edges from S to T. Cosider ay DFS tree T of a udirected graph G rooted at some vertex v. Recall that ay edge of G is either a arc of T or a back arc, that is, a edge coectig a vertex v to oe of its acestors i T. Hece, if G has o cycle of legth at least t, the ay vertex of T seds at most t 1 arcs to his acestors i T. This meas that m t or that t m/. Note that this argumet shows that ay DFS tree of a udirected graph has depth at least m/. For directed graphs, however, ot all arcs are tree arcs or back arcs. Nevertheless, the set of back arcs form a feedback arc set, ad hece, if the logest cycle of a digraph G has legth t, the t β(g. It is atural to try ad adapt the DFS approach to the case of Euleria digraphs. Ufortuately, as the followig propositio shows, this approach fails i Euleria digraphs. Propositio 4.1. There is a Euleria digraph G with average degree at least /0 such that some DFS tree of G has depth 4. Proof. We first defie a graph G as follows. Let t be a positive iteger ad let G be a graph cosistig of t vertex sets V 1,...,V t, each of size t. We also have a special vertex r, sog has t + 1 vertices. We ow defie the arcs of G usig the followig iterative process. We have t iteratios, where i iteratio 1 j t we add the followig arcs; we have t arcs poitig from r to the t vertices of V j, the a matchig from the t vertices of V j to the vertices of V j+1, ad i geeral a matchig from V k to V k+1 for every j k t j. We fially have t arcs from V t j+1 to r. We ote that we ca ideed add a ew (disjoit from previous oes matchig betwee ay pair of sets (V k,v k+1 ieach of the t iteratios by relyig o the fact that the edges of the complete bipartite graph K t,t ca be split ito t perfect matchigs. Observe that i iteratio j we add t(t j +3 arcs to G. Hece G has t t(t j +3 t 3 j=1 arcs. Moreover it is easy to see from costructio that G is Euleria. To get the graph G we modify G as follows. For every vertex v t V i we add two ew vertices v i,v out ad add a 4-cycle (r, v i,v,v out,r. We get that G has 6t + 1 vertices ad more tha t 3 arcs, so settig =6t + 1 we see that G has average degree at least /0.
15 Large Feedback Arc Sets ad Log Cycles i Euleria digraphs 873 Now cosider a DFS tree of G which proceeds as follows. We start at r, ad the for every v V t go to v i, the to v, adthetov out.next,foreveryv V t 1 we go to v i, the to v, adthetov out. We cotiue i this way util we cover all the vertices of G. The DFS tree we thus get has r as its root, ad t paths of legth 3 (of type r, v i,v,v out attached to it. Observe that the above propositio does ot rule out the possibility that some DFS tree has depth Ω(m/. We ote that provig such a claim will imply that a Euleria digraph has a path of legth Ω(m/. It appears that eve this special case of the Bollobás Scott cojecture is still ope, so it might be iterestig to ivestigate this problem further. I fact, we suspect that if G is a coected Euleria digraph the for ay vertex v G there is a path of legth Ω(m/ startig at v. This statemet for udirected graphs follows from the DFS argumet at the begiig of this sectio. Ackowledgemet We would like to thak Jacques Verstraete for helpful iitial discussios. We also would like to thak the referee for carefully readig the mauscript ad providig may helpful suggestios. Refereces [1] Alo, N. (006 Rakig touramets. SIAM J. Discrete Math [] Bollobás, B. (1998 Moder Graph Theory, Vol. 184 of Graduate Texts i Mathematics, Spriger. [3] Bollobás, B. ad Scott, A. (1996 A proof of a cojecture of Body cocerig paths i weighted digraphs. J. Combi. Theory Ser. B [4] Caccetta, L. ad Häggkvist, R. (1978 O miimal digraphs with give girth. I Proc. 9th Southeaster Coferece o Combiatorics, Graph Theory, ad Computig: Boca Rato Cogress. Numer. XXI [5] Charbit, P., Thomassé, S. ad Yeo, A. (007 The miimum feedback arc set problem is NP-hard for touramets. Combi. Probab. Comput [6] Chudovsky, M., Seymour, P. ad Sulliva, B. (008 Cycles i dese digraphs. Combiatorica [7] Fox, J., Keevash, P. ad Sudakov, B. (010 Directed graphs without short cycles. Combi. Probab. Comput [8] Leiserso, C. ad Saxe, J. (1991 Retimig sychroous circuitry. Algorithmica [9] Nathaso, M. The Caccetta Häggkvist cojecture ad additive umber theory. [10] Shaw, A. (1974 The Logical Desig of Operatig Systems, Pretice Hall. [11] Sulliva, B. (008 Extremal problems i digraphs. PhD thesis, Priceto Uiversity. [1] Sulliva, B. A summary of results ad problems related to the Caccetta Häggkvist cojecture.
Large feedback arc sets, high minimum degree subgraphs, and long cycles in Eulerian digraphs
 Large feedback arc sets, high minimum degree subgraphs, and long cycles in Eulerian digraphs Hao Huang Jie Ma Asaf Shapira Benny Sudakov Raphael Yuster Abstract A minimum feedback arc set of a directed
Large feedback arc sets, high minimum degree subgraphs, and long cycles in Eulerian digraphs Hao Huang Jie Ma Asaf Shapira Benny Sudakov Raphael Yuster Abstract A minimum feedback arc set of a directed
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
The size Ramsey number of a directed path
 The size Ramsey umber of a directed path Ido Be-Eliezer Michael Krivelevich Bey Sudakov May 25, 2010 Abstract Give a graph H, the size Ramsey umber r e (H, q) is the miimal umber m for which there is a
The size Ramsey umber of a directed path Ido Be-Eliezer Michael Krivelevich Bey Sudakov May 25, 2010 Abstract Give a graph H, the size Ramsey umber r e (H, q) is the miimal umber m for which there is a
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
A Note on Chromatic Transversal Weak Domination in Graphs
 Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Matrix Partitions of Split Graphs
 Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH
 J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
Xiaozhou (Steve) Li, Atri Rudra, Ram Swaminathan. HP Laboratories HPL Keyword(s): graph coloring; hardness of approximation
 Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Average Connectivity and Average Edge-connectivity in Graphs
 Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
INTERSECTION CORDIAL LABELING OF GRAPHS
 INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
An Efficient Algorithm for Graph Bisection of Triangularizations
 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
An Efficient Algorithm for Graph Bisection of Triangularizations
 Applied Mathematical Scieces, Vol. 1, 2007, o. 25, 1203-1215 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045, Oe
Applied Mathematical Scieces, Vol. 1, 2007, o. 25, 1203-1215 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045, Oe
THE COMPETITION NUMBERS OF JOHNSON GRAPHS
 Discussioes Mathematicae Graph Theory 30 (2010 ) 449 459 THE COMPETITION NUMBERS OF JOHNSON GRAPHS Suh-Ryug Kim, Boram Park Departmet of Mathematics Educatio Seoul Natioal Uiversity, Seoul 151 742, Korea
Discussioes Mathematicae Graph Theory 30 (2010 ) 449 459 THE COMPETITION NUMBERS OF JOHNSON GRAPHS Suh-Ryug Kim, Boram Park Departmet of Mathematics Educatio Seoul Natioal Uiversity, Seoul 151 742, Korea
Relationship between augmented eccentric connectivity index and some other graph invariants
 Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Characterizing graphs of maximum principal ratio
 Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Lecture 18. Optimization in n dimensions
 Lecture 8 Optimizatio i dimesios Itroductio We ow cosider the problem of miimizig a sigle scalar fuctio of variables, f x, where x=[ x, x,, x ]T. The D case ca be visualized as fidig the lowest poit of
Lecture 8 Optimizatio i dimesios Itroductio We ow cosider the problem of miimizig a sigle scalar fuctio of variables, f x, where x=[ x, x,, x ]T. The D case ca be visualized as fidig the lowest poit of
Spanning Maximal Planar Subgraphs of Random Graphs
 Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Convergence results for conditional expectations
 Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
Σ P(i) ( depth T (K i ) + 1),
 EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Compactness of Fuzzy Sets
 Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Some cycle and path related strongly -graphs
 Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Sum-connectivity indices of trees and unicyclic graphs of fixed maximum degree
 1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
arxiv: v2 [cs.ds] 24 Mar 2018
![arxiv: v2 [cs.ds] 24 Mar 2018 arxiv: v2 [cs.ds] 24 Mar 2018](/thumbs/81/83887444.jpg) Similar Elemets ad Metric Labelig o Complete Graphs arxiv:1803.08037v [cs.ds] 4 Mar 018 Pedro F. Felzeszwalb Brow Uiversity Providece, RI, USA pff@brow.edu March 8, 018 We cosider a problem that ivolves
Similar Elemets ad Metric Labelig o Complete Graphs arxiv:1803.08037v [cs.ds] 4 Mar 018 Pedro F. Felzeszwalb Brow Uiversity Providece, RI, USA pff@brow.edu March 8, 018 We cosider a problem that ivolves
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Data Structures and Algorithms. Analysis of Algorithms
 Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Planar graphs. Definition. A graph is planar if it can be drawn on the plane in such a way that no two edges cross each other.
 Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
Greedy Algorithms. Interval Scheduling. Greedy Algorithms. Interval scheduling. Greedy Algorithms. Interval Scheduling
 Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Chapter 3 Classification of FFT Processor Algorithms
 Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
On Alliance Partitions and Bisection Width for Planar Graphs
 Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
Mean cordiality of some snake graphs
 Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES
 3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
4-Prime cordiality of some cycle related graphs
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 1, Issue 1 (Jue 017), pp. 30 40 Applicatios ad Applied Mathematics: A Iteratioal Joural (AAM) 4-Prime cordiality of some cycle related
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 1, Issue 1 (Jue 017), pp. 30 40 Applicatios ad Applied Mathematics: A Iteratioal Joural (AAM) 4-Prime cordiality of some cycle related
Super Vertex Magic and E-Super Vertex Magic. Total Labelling
 Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Polynomial Functions and Models. Learning Objectives. Polynomials. P (x) = a n x n + a n 1 x n a 1 x + a 0, a n 0
 Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
EVALUATION OF TRIGONOMETRIC FUNCTIONS
 EVALUATION OF TRIGONOMETRIC FUNCTIONS Whe first exposed to trigoometric fuctios i high school studets are expected to memorize the values of the trigoometric fuctios of sie cosie taget for the special
EVALUATION OF TRIGONOMETRIC FUNCTIONS Whe first exposed to trigoometric fuctios i high school studets are expected to memorize the values of the trigoometric fuctios of sie cosie taget for the special
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
CSE 417: Algorithms and Computational Complexity
 Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Some New Results on Prime Graphs
 Ope Joural of Discrete Mathematics, 202, 2, 99-04 http://dxdoiorg/0426/ojdm202209 Published Olie July 202 (http://wwwscirporg/joural/ojdm) Some New Results o Prime Graphs Samir Vaidya, Udaya M Prajapati
Ope Joural of Discrete Mathematics, 202, 2, 99-04 http://dxdoiorg/0426/ojdm202209 Published Olie July 202 (http://wwwscirporg/joural/ojdm) Some New Results o Prime Graphs Samir Vaidya, Udaya M Prajapati
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Graphs ORD SFO LAX DFW
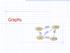 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Visualization of Gauss-Bonnet Theorem
 Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
arxiv: v1 [math.co] 22 Dec 2015
![arxiv: v1 [math.co] 22 Dec 2015 arxiv: v1 [math.co] 22 Dec 2015](/thumbs/92/109673654.jpg) The flag upper boud theorem for 3- ad 5-maifolds arxiv:1512.06958v1 [math.co] 22 Dec 2015 Hailu Zheg Departmet of Mathematics Uiversity of Washigto Seattle, WA 98195-4350, USA hailuz@math.washigto.edu
The flag upper boud theorem for 3- ad 5-maifolds arxiv:1512.06958v1 [math.co] 22 Dec 2015 Hailu Zheg Departmet of Mathematics Uiversity of Washigto Seattle, WA 98195-4350, USA hailuz@math.washigto.edu
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION
 I terat. J. Mh. & Math. Sci. Vol. (1978) 125-132 125 ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION A. W. GOODMAN ad E. B. SAFF* Mathematics Dept, Uiversity of South Florida Tampa, Florida 33620 Dedicated
I terat. J. Mh. & Math. Sci. Vol. (1978) 125-132 125 ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION A. W. GOODMAN ad E. B. SAFF* Mathematics Dept, Uiversity of South Florida Tampa, Florida 33620 Dedicated
Exact Minimum Lower Bound Algorithm for Traveling Salesman Problem
 Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Project 2.5 Improved Euler Implementation
 Project 2.5 Improved Euler Implemetatio Figure 2.5.10 i the text lists TI-85 ad BASIC programs implemetig the improved Euler method to approximate the solutio of the iitial value problem dy dx = x+ y,
Project 2.5 Improved Euler Implemetatio Figure 2.5.10 i the text lists TI-85 ad BASIC programs implemetig the improved Euler method to approximate the solutio of the iitial value problem dy dx = x+ y,
Recursive Procedures. How can you model the relationship between consecutive terms of a sequence?
 6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
On Ryser s conjecture for t-intersecting and degree-bounded hypergraphs arxiv: v2 [math.co] 9 Dec 2017
![On Ryser s conjecture for t-intersecting and degree-bounded hypergraphs arxiv: v2 [math.co] 9 Dec 2017 On Ryser s conjecture for t-intersecting and degree-bounded hypergraphs arxiv: v2 [math.co] 9 Dec 2017](/thumbs/74/70358759.jpg) O Ryser s cojecture for t-itersectig ad degree-bouded hypergraphs arxiv:1705.1004v [math.co] 9 Dec 017 Zoltá Király Departmet of Computer Sciece ad Egerváry Research Group (MTA-ELTE) Eötvös Uiversity Pázmáy
O Ryser s cojecture for t-itersectig ad degree-bouded hypergraphs arxiv:1705.1004v [math.co] 9 Dec 017 Zoltá Király Departmet of Computer Sciece ad Egerváry Research Group (MTA-ELTE) Eötvös Uiversity Pázmáy
Running Time. Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Analysis Metrics. Intro to Algorithm Analysis. Slides. 12. Alg Analysis. 12. Alg Analysis
 Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
DATA STRUCTURES. amortized analysis binomial heaps Fibonacci heaps union-find. Data structures. Appetizer. Appetizer
 Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
THE DIAMETER GAME JÓZSEF BALOGH, RYAN MARTIN, AND ANDRÁS PLUHÁR
 THE DIAMETER GAME JÓZSEF BALOGH, RYAN MARTIN, AND ANDRÁS PLUHÁR Abstract. A large class of the so-called Positioal Games are defied o the complete graph o vertices. The players, Maker ad Breaker, take
THE DIAMETER GAME JÓZSEF BALOGH, RYAN MARTIN, AND ANDRÁS PLUHÁR Abstract. A large class of the so-called Positioal Games are defied o the complete graph o vertices. The players, Maker ad Breaker, take
