arxiv: v1 [math.co] 22 Dec 2015
|
|
|
- Augustus McDaniel
- 5 years ago
- Views:
Transcription
1 The flag upper boud theorem for 3- ad 5-maifolds arxiv: v1 [math.co] 22 Dec 2015 Hailu Zheg Departmet of Mathematics Uiversity of Washigto Seattle, WA , USA August 28, 2018 Abstract We prove that amog all flag 3-maifolds o vertices, the joi of two circles with 2 ad 2 vertices respectively is the uique maximizer of the face umbers. This solves the first case of a cojecture due to Lutz ad Nevo. Further, we establish a sharp upper boud o the umber of edges offlag 5-maifolds ad characterizethe casesof equality. We alsoshow that the iequality part of the flag upper boud cojecture cotiues to hold for all flag 3-dimesioal Euleria complexes ad fid all maximizers of the face umbers i this class. 1 Itroductio Oe of the classical problems i geometric combiatorics deals with the followig questio: for a give class of simplicial complexes, fid tight upper bouds o the umber of i-dimesioal faces as a fuctio of the umber of vertices ad the dimesio. Sice Motzki [13] proposed the upper boud cojecture (UBC, for short) for polytopes i 1957, this problem has bee solved for various families of complexes. I particular, McMulle [12] ad Staley [17] proved that eighborly polytopes simultaeously maximize all face umbers i the class of polytopes ad simplicial spheres. However, it turs out that, apart from cyclic polytopes, may other classes of eighborly spheres or eve eighborly polytopes exist, see [16] ad [15] for examples ad costructios of eighborly polytopes. A simplicial complex is flag if all of its miimal o-faces have cardiality two, or equivaletly, is the clique complex of its graph. Flag complexes form a beautiful ad importat class of simplicial complexes. For example, barycetric subdivisios of simplicial complexes, order complexes of posets, ad Coxeter complexes are flag complexes. Despite a lot of effort that wet ito studyig the face umbers of flag spheres, i particular i relatio with the Charey-Davis cojecture [5], ad its geeralizatio give by Gal s cojecture [9], a flag upper boud theorem for spheres is still ukow. The upper bouds o face umbers for geeral simplicial (d 1)-spheres are far from beig sharp for flag (d 1)-spheres, sice the graph of ay flag (d 1)-dimesioal complex is K d+1 -free. I [9], Gal cofirmed that the real rootedess cojecture [7] does hold for flag homology spheres of dimesio less tha five, ad thus the upper bouds o the face umbers of these flag spheres were established. However, startig from dimesio five, there are oly cojectural upper bouds. For m 1, we let J m () be the (2m 1)-sphere o vertices obtaied as the joi of m copies of the circle, each oe a cycle with either m or m vertices. The followig cojecture is due to Nevo ad Peterse [14, Cojecture 6.3]. 1
2 Cojecture 1.1. If is a flag homology sphere, the γ( ) satisfies the Frakl-Füredi-Kalai iequalities. I particular, if is of dimesio d = 2m 1, the f i ( ) f i (J m ()) for all 1 i 2m 1. Here we deote by f i ( ) the umber of i-dimesioal faces of ; the etries of the vector γ( ) are certai liear combiatios of the f-umbers of. For Frakl-Füredi-Kalai iequalities, see [8]. As for the case of equality, Lutz ad Nevo [11, Cojecture 6.3] posited that, as opposed to the case of all simplicial spheres, for a fixed dimesio 2m 1 ad the umber of vertices, there is oly oe maximizer of the face umbers. Cojecture 1.2. Let m 2 ad let be a flag simplicial (2m 1)-sphere o vertices. The f i ( ) = f i (J m ()) for some 1 i m if ad oly if = J m (). Recetly, Adamaszek ad Hladký [2] proved that Cojecture 1.2 holds asymptotically for flag homology maifolds. Several celebrated theorems from extremal graph theory served as tools for their work. As a result, the proof simutaeously gives upper bouds o f-umbers, h-umbers, g-umbers ad γ-umbers, but it oly applies to flag homology maifolds with a extremely large umber of vertices. Our first mai result is that Cojecture 1.1 ad 1.2 hold for all flag 3-maifolds. I particular, we show that the balaced joi of two circles is the uique maximizer of face umbers i the class of flag 3-maifolds. We also establish a aalogous result o the umber of edges of flag 5-maifolds. The proof oly relies o simple properties of flag complexes ad Euleria complexes. I 1964, Klee [10] proved that Motzki s UBC for polytopes holds for a much larger class of Euleria complexes as log as they have sufficietly may vertices, ad cojectured that the UBC holds for all Euleria complexes. Our secod mai result deals with flag Euleria complexes, ad asserts that Cojecture 1.1 cotiues to hold for all flag 3-dimesioal Euleria complexes. This provides supportig evidece to a questio of Adamaszek ad Hladký [2, Problem 17(i)] i the case of dimesio 3, where they proposed that Cojecture 1.1 holds for all odd-dimesioal flag weak pseudomaifolds with sufficietly may vertices. We also give costructios of the maximizers of face umbers i this class ad show that they are the oly maximizers. Our proof is based o a applicatio of the iclusio-exclusio priciple ad double coutig. The paper is orgaized as follows. I Sectio 2, we discuss basic facts o simplicial complexes ad flag complexes. I Sectio 3, we provide the proof of our first mai result assertig that give a umber of vertices, the maximum face umbers of a flag 3-maifold are achieved oly whe this maifold is the joi of two circles of legth as close as possible to 2. I Sectio 4, we apply a aalogous argumet to the class of flag 5-maifolds. I Sectio 5, we show that the same upper bouds cotiue to hold for the class of flag 3-dimesioal Euleria complexes, ad discuss the maximizers of the face umbers i this class. Fially, we close i Sectio 6 with some cocludig remarks. 2 Prelimiaries A simplicial complex o a vertex set V = V( ) is a collectio of subsets σ V, called faces, that is closed uder iclusio. For σ, let dimσ := σ 1 ad defie the dimesio of, dim, as the maximal dimesio of its faces. A facet i is a maximal face uder iclusio, ad we say that is pure if all of its facets have the same dimesio. We will deote by the disjoit uio of simplicial complexes, ad by the disjoit uio of sets. 2
3 If is a simplicial complex ad σ is a face of, the lik of σ i is lk σ := {τ σ : σ τ }, ad the deletio of a vertex set W from is \W := {σ : σ W = }. The restrictio of to a vertex set W is defied as [W] := {σ : σ W}. If ad Γ are two simplicial complexes o disjoit vertex sets, the the joi of ad Γ, deoted as Γ, is the simplicial complex o vertex set V( ) V(Γ) whose faces are {σ τ : σ,τ Γ}. A simplicial complex is a simplicial maifold (resp. simplicial sphere) if the geometric realizatio of is homeomorphic to a maifold (resp. sphere). We deote by H ( ;k) the reduced homology of computedwithcoefficiets iafieldk, adbyβ i ( ;k) := dim k Hi ( ;k)thereduced Betti umbers of with coefficiets i k. We say that is a (d 1)-dimesioal k-homology maifold if H (lk σ;k) = H (S d 1 σ ;k) for every oempty face σ. A k-homology sphere is a k-homology maifold that has the k-homology of a sphere. Every simplicial maifold (resp. simplicial sphere) is a homology maifold (resp. homology sphere). Moreover, i dimesio two, the class of homology 2-spheres coicides with that of simplicial 2-spheres, ad hece i dimesio three, the class of homology 3-maifolds coicides with that of simplicial maifolds. For a (d 1)-dimesioal complex, we let χ( ) := d 1 i=0 ( 1)i β i ( ;k) be the reduced Euler characteristic of. A simplicial complex is called a Euleria complex if is pure ad χ(lk σ) = ( 1) dimlk σ for every σ, icludig σ =. I particular, it follows from the Poicaré duality theorem that all odd-dimesioal orietable homology maifolds are Euleria. As all simplicial maifolds are orietable over Z/2Z, all odd-dimesioal simplicial maifolds are Euleria. A (d 1)-dimesioal simplicial complex is called a weak (d 1)-pseudomaifold if it is pure ad every (d 2)-face (called ridge) of is cotaied i exactly two facets. A weak (d 1)- pseudomaifold is called a ormal (d 1)-pseudomaifold if it is coected, ad the lik of each face of dimesio d 3 is also coected. Every Euleria complex is a weak pseudomaifold, ad every coected homology maifold is a ormal pseudomaifold. I fact, every ormal 2- pseudomaifold is also a homology 2-maifold. However, for d > 3, the class of ormal (d 1)- pseudomaifolds is much larger tha the class of homology (d 1)-maifolds. It is well-kow that if is a weak (resp. ormal) (d 1)-pseudomaifold ad σ is a face of of dimesio at most d 2, the the lik of σ is also a weak (resp. ormal) pseudomaifold. The followig lemma gives aother property of ormal pseudomaifolds, see [4, Lemma 1.1]. Lemma 2.1. Let be a ormal (d 1)-pseudomaifold, ad let W be a subset of vertices of such that the iduced subcomplex [W] is a ormal (d 2)-pseudomaifold. The the iduced subcomplex of o vertex set V( )\W has at most two coected compoets. For a (d 1)-dimesioal complex, we let f i = f i ( ) be the umber of i-dimesioal faces of for 1 i d 1. The vector (f 1,f 0,,f d 1 ) is called the f-vector of. Sice the graph of ay simplicial 2-sphere is a maximal plaar graph, it follows that the f-vector of a simplicial 2-sphere is uiquely determied by f 0. For a 3-dimesioal Euleria complex, the followig lemma idicates that its f-vector is uiquely determied by f 0 ad f 1. Lemma 2.2. The f-vector of a 3-dimesioal Euleria complex satisfies (f 0,f 1,f 2,f 3 ) = (f 0,f 1,2f 1 2f 0,f 1 f 0 ). Proof: Let be a 3-dimesioal Euleria complex. Sice is Euleria, χ( )+1 = f 0 f 1 + f 2 f 3 = 0. Also sice every ridge of a Euleria complex is cotaied i exactly two facets, by double coutig, we obtai that 2f 2 = 4f 3. Hece the result follows. 3
4 A simplicial complex is flag if all miimal o-faces of, also called missig faces, have cardiality two; equivaletly, is the clique complex of its graph. The followig lemma [14, Lemma 5.2] gives a basic property of flag complexes. Lemma 2.3. Let be a flag complex o vertex set V. If W V, the [W] is also flag. Furthermore, if σ is a face i, the lk σ = [V(lk σ)]. I particular, all liks i a flag complex are also flag. Fially, we recall some termiology from graph theory. A graph G is a path graph if the set of its vertices ca be ordered as x 1,x 2,,x i such a way that {x i,x i+1 } is a edge for all 1 i 1 ad there are o other edges. Similarly, a cycle graph is a graph obtaied from a path graph by addig a edge betwee the edpoits of the path. 3 The Proof of the Lutz-Nevo Cojecture for flag 3-maifolds The goal of this sectio is to prove Cojecture 1.2 for 3-dimesioal maifolds. We start by settig up some otatio ad establishig several lemmas that will be used i the proof. Recall that i the Itroductio, we defied J m () to be the (2m 1)-sphere o vertices obtaied as the joi of m circles, each oe of legth either m or m. I the followig, we defie J m() as the suspesio of J m ( 2), ad deote by Cd the (d 1)-dimesioal octahedral sphere, i.e., the boudary complex of the d-dimesioal cross-polytope. Equivaletly, Cd is a d-fold joi of S0, ad thus C2m = J m(4m) ad C2m+1 = J m (4m + 2). The followig lemma [14, Lemma 5.3], origially stated for the class of flag homology spheres, gives a sufficiet coditio for a flag ormal pseudomaifold to be a octahedral sphere. (As the proof is idetical to that of [14, Lemma 5.3], we omit it.) Lemma 3.1. Let be a (d 1)-dimesioal flag ormal pseudomaifold o vertex set V such that for ay v V, lk v is a octahedral sphere. The is a octahedral sphere. Next we characterize all flag ormal (d 1)-pseudomaifolds o 2d+1 vertices. Lemma 3.2. Let ba a flag ormal (d 1)-pseudomaifold, where d 2. The (a) f 0 ( ) 2d. Equality holds if ad oly if = C d. (b) f 0 ( ) = 2d+1 if ad oly if = J 1 (5) C d 2, or equivaletly, = J m(4m +1) if d = 2m, ad = J m(4m+3) if d = 2m+1. Proof: Part (a) is well-kow, see the proof of Propositio 2.2 i [3]. For part (b), we use iductio o the dimesio. If d = 2 ad f 0 ( ) = 5, the is a circle of legth 5, that is, J 1 (5). Now assume that the claim holds for d < k, ad cosider a flag ormal (k 1)-pseudomaifold o 2k +1 vertices. Sice lk v is a flag ormal pseudomaifold for ay vertex v, by part (a), f 0 (lk v) 2k 2. Moreover, if equality holds, the lk v is a octahedral sphere. However, if f 0 (lk v) = 2k 2 for every vertex v, the by Lemma 3.1, must be the octahedral sphere of dimesio k 1, cotradictig that f 0 ( ) = 2k+1. Hece there is at least oe vertex u such that f 0 (lk u) 2k 1. Sice is a ormal pseudomaifold, for ay facet σ lk u, lk σ cosists of two vertices. O the other had, sice is flag, lk u is also flag by Lemma 2.3, ad hece lk σ does ot cotai ay vertex i V(lk u). It follows that f 0 (lk u) (2k+1) 2 = 2k 1. Therefore, f 0 (lk u) = 2k 1, ad the liks of all facets of lk u are the same two vertices. This implies that is the suspesio of lk u. By iductio, lk u = J 1 (5) Cd 3, ad hece = J 1(5) Cd 2. Now we estimate the umber of edges i a flag ormal 3-pseudomaifold o vertices. 4
5 Lemma 3.3. Let be a flag ormal 3-pseudomaifold o vertices. The f 1 ( ) f 1 (J 2 ())+c, where c = 3 3mi v χ(lk v). Proof: Let v be a vertex of maximum degree i V( ). We let a = f 0 (lk v), W 1 = V(lk v) ad W 2 = V( )\V(lk v). Sice is a ormal 3-pseudomaifold, lk v is a ormal 2-pseudomaifold, i.e., a simplicial 2-maifold. Furthermore, sice is flag, by Lemma 2.3, lk v is the restrictio of to W 1. Thus, by Lemma 2.1, the iduced subcomplex [W 2 ] has at most two coected compoets. Sice v is ot coected to ay vertices i W 2 \{v}, it follows that {v} ad [W 2 \{v}] are the two coected compoets i [W 2 ]. We ow cout the edges of. They cosist of the edges of [W 1 ] = lk v, the edges of [W 2 ] ad the edges betwee these two sets. I additio, w W 2 f 0 (lk w) couts the edges of [W 2 ] twice. Thus, ( ) f 1 ( ) = f 1 ( [W 1 ])+ f 0 (lk w) f 1 ( [W 2 ]) w W 2 ( ) f 1 (lk v)+ W 2 max w W 2 f 0 (lk w) (f 0 ( [W 2 \{v}]) 1) ( ) = ( 3a 6+3(1 χ(lk v)) ) +( a)a ( a 2) = a 2 +a(+4) (+4)+3 3χ(lk v) ( ) χ(lk v) 4 = f 1 (J 2 ( ))+3(1 χ(lk v)). Here i (*) we used that [W 2 \{v}] is coected ad hece has at least f 0 ( [W 2 \{v}]) 1 edges. Equality (**) follows from the fact that lk v is a 2-maifold with a vertices, ad (***) is obtaied by optimizig the fuctio p(a) = a 2 +a(+4). Hece the result follows. (3.1) Theorem 3.4. Let be a flag 3-maifold o vertices. The f i ( ) f i (J 2 ()). If equality holds for some 1 i 3, the = J 2 (). Proof: We use the same otatio as i the proof of Lemma 3.3. That is, we let v be a vertex of maximum degree i V( ). We let a = f 0 (lk v), W 1 = V(lk v) ad W 2 = V( )\V(lk v). Sice is a flag 3-maifold, χ(lk w) = 1 for every w. Hece by Lemma 3.3, f 1 ( ) f 1 (J 2 ( )). Furthermore, it follows from steps (*) ad (***) i equality (3.1) that f 1 ( ) = f 1 (J 2 ()) holds oly if f 0 (lk w) = a = +4 2 or +4 2 for all w W2, ad [W 2 \{w}] is a tree. We claim that if f 1 ( ) = f 1 (J 2 ()), the = J 2 (). This ideed holds if = 8 or 9, sice by Lemma 3.2, the oly flag 3-maifolds o 8 or 9 vertices are J 2 (8) ad J 2 (9). Next we assume that 10, where W 2 = a 2 2 > 2. Hece the tree [W2 \{v}] has at least oe edge, ad thus there is a vertex u 1 W 2 such that deg [W2 ]u 1 = 1. Let u 2 be the uique vertex i W 2 that is coected to u 1. Sice f 0 (lk u 1 ) = a, the vertex u 1 must be coected to all vertices i W 1 except for oe vertex. We let z 1 be this vertex ad deote the circle lk lk vz 1 by C 1. Sice is flag, lk u 1 [W 1 \{z 1 }] = lk v {z 1 } C 1, ad hece lk u 1 = (lk v {z 1 } C 1 ) ({u 2 } C 1 ). 5
6 If {z 1 } lk u 2, the lk u 2 C 1 {u 1,z 1 }. Sice C 1 {u 1,z 1 } is a 2-sphere, it follows that lk u 2 = C 1 {u 1,z 1 } ad f 0 (C 1 ) = a 2. Hece W 2 = {u 1,u 2 } ad W 1 = V(C 1 ) {z 1 } {z 2 } for some vertex z 2 W 1, so that lk v = {z 1,z 2 } C 1. Now assume that {z 1 } / lk u 2 ad u 2 is coected to vertices u 3,u 4,,u k i [W 2 ]. Sice C 1 is a circle i the 2-sphere lk u 2, the subcomplex lk u 2 \V(C 1 ) has two cotractible coected compoets. If there is a vertex u i such that lk lk u 2 u i = C 1, the lk u 2 C 1 {u 1,u i } ad hece this lik is exactly C 1 {u 1,u i }. This implies that deg [W2 ]u 2 = 2. Otherwise, if lk lk u 2 u i C 1 for all 3 i k, the each u i is coected to at least oe vertex i lk v\(v(c 1 ) {z 1 }). Sice lk u 1 lk v\{z 1 }, it follows that the vertices u 1 ad u 3,,u k are i the same coected compoet, ad hece lk u 2 \V(C 1 ) is coected, a cotradictio. By applyig the above argumet iductively, we obtai that [W 2 \{v}] is a path graph (u 1,u 2,,u a 1 ), ad there is a vertex z 2 i W 1 such that lk u 1 = {z 2,u 2 } C 1 ad lk v = C 1 {z 1,z 2 }. Furthermore, C 1 lk u i for all u i W 2. The we let C 2 be the cycle graph (v,z 2,u 1,u 2,,u a 1,z 1 ). It follows that = C 1 C 2. Sice a = C 1 +2 = +4 2 or +4 4, C 1 ad C 2 must be cycles of legth 2 or 2. This implies = J 2(). By Lemma 2.2, the f-vector of is uiquely determied by f 0 ( ) = ad f 1 ( ). This yields the result. 4 Coutig edges of flag 5-maifolds For eve-dimesioal flag simplicial spheres, we have the followig weaker form of the flag upper boud cojecture, see Cojecture 18 i [2]: Cojecture 4.1. Fix m 1. For every flag 2m-sphere o vertices, we have f 1 (M) f 1 (J m ()). Usig almost the same argumet as i the proof of Theorem 3.4, we establish the followig propositio. Propositio 4.2. Let be a flag (2m+1)-maifold o vertices. If Cojecture 4.1 holds for all flag 2i-spheres with 1 i m, the f 1 ( ) f 1 (J m+1 ()). Equality holds oly whe = J m+1 (). Proof: The proof is by iductio o m. The case m = 1 is cofirmed by Theorem 3.4. Now assume that m 2 ad is a flag (2m+1)-maifold o vertices. If q mod m (0 q < m), the a simple computatio shows that f 1 (J m ()) = m 1 q(q m) 2m m, f 1(Jm m 1 q(q m) ()) = 2m ( 2)2 +3( 2)+ 2m. (4.1) As i the proof of Lemma 3.3, we let v be a vertex of maximum degree i V( ), a = f 0 (lk v), W 1 = V(lk v) ad W 2 = V( )\V(lk v). Followig the same argumet as i Lemma 3.3, we obtai the followig aalog of (3.1): f 1 ( ) f 1 (J m(a))+ W 2 max w W 2 f 0 (lk w) (f 0 ( [W 2 \{v}]) 1) ( ) m 1 2m (a 2)2 +3(a 2)+ = m+1 2m q(q m) 2i ( a ( m m+1 +2)) 2 + m 2m ( a)a ( a 2) q(q m), 2r
7 where i ( ) we used our assumptio that Cojecture 4.1 holds for flag 2m-spheres. By (4.1), m m+1 f 1 (J m+1 ()) = m 2m q(q m 1). 2r m m+1 +2 or Hece we coclude that f 1 ( ) f 1 (J m+1 ()). Moreover, equality holds whe a = a = +2, ad [W 2 \{w}] is a tree. If = 4m+4 or 4m+5, the by Lemma 3.2, is either J m+1 (4m + 4) or J m+1 (4m +5). If > 4m +5, the the tree [W 2 \{w}] has at least oe edge. We proceed with the same argumet as i Theorem 3.4 to show that lk v must be the suspesio of a (2m 1)-sphere o either m m+1 or m m+1 vertices. By iductio, this sphere is the joi of m circles, each havig legth either or. Hece = J m+1 (). m+1 m+1 Theorem 4.3. Let be a flag 5-maifold o vertices. The f 1 ( ) f 1 (J 3 ()). Equality holds if ad oly if = J 3 (). Proof: The result follows from Propositio 4.2 ad the fact that Cojecture 4.1 is kow to hold i the case of dimesio four (see [9], Theorem 3.1.3). 5 The face umbers of flag 3-dimesioal Euleria complexes I Lemma 3.3, we established a upper boud o the umber of edges for all flag ormal 3- pseudomaifolds. I this sectio, we fid sharp upper bouds o the face umbers for all flag 3-dimesioal Euleria complexes. The proof relies o the followig three lemmas. Lemma 5.1. Let be a flag (d 1)-dimesioal simplicial complex. (a) If σ 1 ad σ 2 are two ridges that lie i the same facet σ i, the the liks of σ 1 ad σ 2 are disjoit. (b) If σ = τ 1 τ 2 is a face i, the V(lk τ 1 ) V(lk τ 2 ) = V(lk σ). I particular, if σ is a facet, the f 0 (lk τ 1 )+f 0 (lk τ 2 ) f 0 ( ). Proof: For part (a), if v is a commo vertex of lk σ 1 ad lk σ 2, the v must be adjacet to each vertex of σ 1 σ 2 = σ. Thus, sice is flag, {v} σ, which cotradicts our assumptio that σ is a facet. For part (b), the iclusio V(lk τ 1 ) V(lk τ 2 ) V(lk σ) holds for ay simplicial complex. If v V(lk τ 1 ) V(lk τ 2 ), the v τ 1,v τ 2. Sice is flag, it follows that v σ. If σ is ot a facet, the v lk σ. This implies V(lk τ 1 ) V(lk τ 2 ) V(lk σ). However, if σ is a facet, the v σ caot a facet i. I this case, V(lk τ 1 ) V(lk τ 2 ) = V(lk σ) =, ad so f 0 (lk τ 1 )+f 0 (lk τ 2 ) f 0 ( ). Lemma 5.1 part (b) implies that if is a flag 3-dimesioal simplicial complex ad σ is a facet, the e σ f 0(lk e) 3f 0 ( ), where the sum is over the edges of σ. The followig lemma suggests a better estimate o e σ f 0(lk e) if is a flag weak 3-pseudomaifold. 7
8 Lemma 5.2. Let be a flag weak 3-pseudomaifold o vertices. The for ay facet σ = {v 1,v 2,v 3,v 4 } of, e σ f 0(lk e) + 16, where the sum is over the edges of σ. If equality holds, the w τ V(lk w) = V( ) for ay ridge τ σ. Proof: Let V i = V(lk v i ) for 1 i 4. By Lemma 5.1 part (b), for ay distict 1 i,j 4, we have V i V j = V(lk {v i,v j }) ad V 1 V 2 V 3 V 4 = V(lk σ) =. Also sice is a weak 3-pseudomaifold, ay ridge of is cotaied i exactly two facets. Hece V i V j V k = V(lk {v i,v j,v k }) is a set of cardiality two. By the iclusiog-exclusio priciple, we obtai that V i V j = V 1 V 2 V 3 V 4 + V i + V i V j V k V 1 V 2 V 3 V 4 1 i<j 4 = 1 i 4 1 i 4 V i V 1 V 2 V 3 V i<j<k 4 ( ) 4 3 = ( V 1 + V 2 V 1 V 2 )+( V 3 + V 4 V 3 V 4 )+ (V 1 V 2 ) (V 3 V 4 ) +8 = V 1 V 2 + V 3 V 4 + (V 1 V 2 ) (V 3 V 4 ) +8. For simplicity, we deote the set (V 1 V 2 ) (V 3 V 4 ) as V. Notice that by Lemma 5.1 part (b), ay vertex v belogs to at most oe of the sets V 1 V 2 ad V 3 V 4. We split the vertices of ito the followig three types. 1. If v V 1 V 2 ad v / V 3 V 4, or if v V 3 V 4 ad v / V 1 V 2, the v / V. Each of these vertices cotributes 1 to the right-had side of (5.1). 2. If v V i V j V k for some triple {i,j,k} [4], the v belogs to either V 1 V 2 or V 3 V 4, ad v V. By Lemma 5.1 part (a), every pair of ridges i σ has disjoit liks. Sice V i V j V k = 2, the umber of such vertices is exactly 8, ad each of them cotributes 2 to the right-had side of (5.1). 3. If v / V 1 V 2 ad v / V 3 V 4, the v cotributes to the right-had side of (5.1) at most 1. This case occurs oly whe v V, that is, whe v belogs to oe of V 1 ad V 2, ad oe of V 3 ad V 4. Hece {i,j} [4] V i V j +8+8 = +16. Furthermore, if equality holds, the for every vertex v i, either v V 1 V 2, or v V 3 V 4, or v V. This implies that every vertex i belogs to at least two of the four liks lk v 1,,lk v 4. This proves the secod claim. Lemma 5.3. Let be a flag weak 3-pseudomaifold o vertices, ad let σ = {v 1,v 2,v 3,v 4 } be a arbitrary facet of. The 1 i 4 f 0(lk v i ) 2+8. If equality holds, the w τ V(lk w) = V( ) for ay ridge τ σ. Proof: As i Lemma 5.2, we let V i = V(lk v i ). By the iclusio-exclusio priciple, V i = V i V j V i V j V k + V 1 V 2 V 3 V 4 + V 1 V 2 V 3 V 4 1 i 4 1 i<j 4 = 1 i<j 4 1 i<j<k 4 V i V j + V 1 V 2 V 3 V = (5.1) 8
9 The last iequality follows from Lemma 5.2 ad the fact that V 1 V 2 V 3 V 4 V( ) =. The secod claim also follows from Lemma 5.2. Now we are ready to prove the mai result i this sectio. Theorem 5.4. Let be a flag 3-dimesioal Euleria complex o vertices. The f 1 ( ) f 1 (J 2 ()). Proof: We deote the vertices of by v 1,v 2,,v, ad we let a i = f 0 (lk v i ). Sice lk v i is a 2-dimesioal Euleria complex, the f-umbers of lk v i satisfy the relatios f 2 f 1 +f 0 = 2, 3f 2 = 2f 1. Hece f 2 (lk v i ) = 2a i 4. By double coutig, we obtai that f 0 (lk v) = σ, σ =4 v σ f 0 (lk v i ) #{σ : v i σ, σ = 4} = i=1 a i (2a i 4). (5.2) i=1 By Lemma 5.3, the left-had side of (5.2) is bouded above by f 3 ( )(2 + 8), which also equals (f 1 ( ) )(2 + 8) by Lemma 2.2. However, sice 2f 1 ( ) = i=1 f 0(lk v 1 ) = i=1 a i, the right-had side of (5.2) is bouded below by 2f 1( ) (4f 1 ( ) 4 ), ad equality holds oly if a i = 2f 1( ) for all 1 i. Hece, (f 1 ( ) )(2+8) 2f ( 1( ) 4f1 ( ) ) 4. We simplify this iequality to get 8 ) (f 1 ( ) )( f 1( ) (2+8) 0. Sice f 1 ( ), it follows that f 1 ( ) 2 4 +, that is, f 1 ( ) f 1 (J 2 ()). The followig corollary provides some properties of the maximizers of the face umbers i the class of flag 3-dimesioal Euleria complexes. Corollary 5.5. Let be a flag 3-dimesioal Euleria complex o vertices. The f 1 ( ) = f 1 (J 2 ()) if ad oly if (i) 2 vertices of satisfy f0 (lk v) = 2 +2 while 2 vertices satisfy f 0 (lk v) = 2 +2, ad (ii) ad all of its vertex liks are coected. Proof: Part (i) of the claim follows from the proof of Theorem 5.4. Also by Theorem 5.4, if f 1 ( ) = f 1 (J 2 ()), the v σ f 0(lk v) = 2+8foreveryfacetσ = {v 1,v 2,v 3,v 4 }. ByLemma 5.3, every vertex of belogs to 1 i 3 V(lk v i ), ad hece is coected. If there is a vertex v such that lk v is ot coected, the we let τ 1 = {u 1,u 2,u 3 } ad τ 2 = {w 1,w 2,w 3 } be two 2-faces i distict coected compoets of lk v. Sice is flag, by Lemma 2.3, lk v = [V(lk v)]. Therefore o edges exist betwee τ 1 ad τ 2. However, Theorem 5.4 ad Lemma 5.3 also imply that 1 i 3 V(lk u i ) = V( ), cotradictig the fact that {w 1,w 2,w 3 } V(lk u i ) for all 1 i 3. Hece every vertex lik i is coected. The ext lemma, which might be of iterest i its ow right, provides a sufficiet coditio for a flag complex to be the joi of two of its liks. 9
10 Lemma 5.6. Let be a flag (d 1)-dimesioal simplicial complex. If σ = τ 1 τ 2 is a facet of, where τ 1 is a i-face of ad τ 2 is a (d i 2)-face of, the V(lk τ 1 ) V(lk τ 2 ) = V( ) implies that lk τ 1 lk τ 2. Moreover, if is a flag ormal (d 1)-pseudomaifold, the V(lk τ 1 ) V(lk τ 2 ) = V( ) if ad oly if = lk τ 1 lk τ 2. Proof: Sice is flag, [V(lk τ j )] = lk τ j for j = 1,2. Hece for every i-face τ 2 i lk τ 1, the lik lk τ 2 does ot cotai ay vertex i lk τ 1. This implies lk τ 2 lk τ 2. Similarly, for every (d i 2)-face τ 1 lk τ 2, we have lk τ 1 lk τ 1. Thus, lk τ 1 lk τ 2. If is a ormal pseudomaifold, the both lk τ 2 ad lk τ 2 are ormal pseudomaifolds. Sice o proper subcomplex of a ormal pseudomaifold ca be a ormal pseudomaifold of the same dimesio, it follows that lk τ 2 = lk τ 2. Similarly, for every (d i 2)-face τ 1 lk τ 2, lk τ 1 = lk τ 1. Hece = lk τ 1 lk τ 2. Remark 5.7. The secod result i Lemma 5.6 does ot hold for flag weak pseudomaifolds, eve assumig coectedess. Ideed, let L 1,,L 4 be four distict circles of legth 4. The = (L 1 L 3 ) (L 2 L 3 ) (L 1 L 4 ) is a flag weak 3-pseudomaifold. If τ 1 ad τ 2 are edges i L 1 ad L 3 respectively, the lk τ 1 = L 3 L 4 ad lk τ 2 = L 1 L 2. Hece V(lk τ 1 ) V(lk τ 2 ) = V( ). However, is a proper subcomplex of lk τ 1 lk τ 2. I Theorem 3.4 we proved that the maximizer of the face umbers is uique i the class of flag 3-maifolds o vertices. Is this also true for flag 3-dimesioal Euleria complexes? Corollary 5.5 implies that if the case of equality is ot a joi of two circles, the some of its edge liks are ot coected. Motivated by the example i Remark 5.7, we costruct a family of flag 3-dimesioal Euleria complexes o vertices that have the same f-umbers as those of J 2 (). Example 5.8. We write C i to deote a circle of legth i. For a fixed umber 8, let a 1,a 2,,a s, b 1,b 2,,b t 4 be itegers such that a i = ad 2 b j =. 2 1 i s 1 j t We claim that = 1 i s,1 j t (C a i C bj ) is flag ad Euleria, where all C have disjoit vertex sets. Sice the circles C ai ad C bj are of legth 4, they are flag ad hece is also flag. Also ay ridge τ i ca be expressed as τ = v e, where v is a vertex of C ai ad e is a edge of C bj (or v C bj ad e C ai ) for some i,j. By the costructio of, the ridge τ is cotaied i exactly two facets {v,v } e ad {v,v } e of, where v ad v are eighbors of v i the circle C ai (or C bj ). Hece the liks of ridges i are Euleria. Sice the edge liks i are either circles or disjoit uios of circles, ad the vertex liks i are suspesios of disjoit uio of circles, these liks are also Euleria. Fially, the vertices i C ai have degree 2 +2 ad the vertices i Cbj have degree 2, ad thus f1 ( ) = f 1 (J 2 ()). A simple computatio also shows that f 2 ( ) = f 2 (J 2 ()) ad f 3 ( ) = f 3 (J 2 ()). Hece χ( ) = χ(j 2 ()), ad is Euleria. We deote the set of all complexes o vertices costructed i Example 5.8 as GJ(). It turs out that GJ() is exactly theset of maximizers oftheface umbersi theclass of flag3-dimesioal Euleria complex o vertices. To prove this, we begi with the followig lemma. Lemma 5.9. Let be a flag 3-dimesioal Euleria complex o vertices. If f 1 ( ) = f 1 (J 2 ()), the every vertex lik is the suspesio of disjoit uio of circles. 10
11 Proof: Assume that v is a arbitrary vertex of ad deote lk v by Γ. Sice f 1 ( ) = f 1 (J 2 ()), by the proof of Theorem 5.4 ad Lemma 5.3, it follows that for every 2-face {v 1,v 2,v 3 } Γ, we have 1 i 3 V(lk v i ) = V( ). I particular, 1 i 3 V(lk Γ v i ) = 1 i 3 V(lk v i [V(Γ)]) = V(Γ). Sice f 0 (lk Γ v i lk Γ v j ) = 2 for 1 i < j 3 ad f 0 ( 3 i=1 lk Γv i ) = 0, by the iclusio-exclusio priciple, 3 f 0 (lk Γ v i ) = f 0 (Γ)+ i=1 1 i<j 3 f 0 (lk Γ v i lk Γ v j ) f 0 ( 3 i=1lk Γ v i ) = f 0 (Γ)+6. Also sice Γ is Euleria, the f-vector of Γ is (f 0 (Γ),3f 0 (Γ) 6,2f 0 (Γ) 4). Moreover, every vertex lik i Γ is the disjoit uio of circles, ad hece f 0 (lk Γ v) = f 1 (lk Γ v). By double coutig, σ Γ, σ =3 v σf 0 (lk Γ v) = v Γf 0 (lk Γ v) #{σ : v σ, σ = 3} = v σ f 0 (lk Γ v) 2. (5.3) The left-had side of (5.3) equals f 2 (Γ)(f 0 (Γ) + 6) = 2(f 0 (Γ) 2)(f 0 (Γ) + 6). However, sice v σ f 0(lk Γ v) = 2f 1 (Γ) = 6f 0 (Γ) 12, ad every vertex lik i Γ has at least four vertices, the right-had side of (5.3) is bouded above by 2(f 0 (Γ) 2)+(f 0 (Γ) 2) 4 2 = 2(f 0 (Γ) 2)(f 0 (Γ)+6). The the equality forces the right-had side to obtai its maximum. Therefore, there exists two vertices u 1,u 2 Γ whose vertex liks i Γ have f 0 (Γ) 2 vertices ad the other vertex liks have 4 vertices. If f 0 (Γ) = 6, the Γ is the cross-polytope. Else if f 0 (Γ) > 6, the f 0 (lk Γ u 1 ) > 4. Sice Γ is flag, by Lemma 2.3, Γ[V(lk Γ u 1 )] = lk Γ u 1, ad hece every vertex of lk Γ u 1 is ot coected to f 0 (lk Γ u 1 ) 3 > 1 vertices i lk Γ u 1. This implies that u 2 / lk Γ u 1. Hece lk Γ u 2 = Γ[V(Γ)\{u 1,u 2 }] = lk Γ u 1, ad Γ is the joi of lk Γ u 1 ad two vertices u 1,u 2. Theorem Let be a flag 3-dimesioal Euleria complex o vertices. If f 1 ( ) = f 1 (J 2 ()), the GJ(). Proof: By Lemma 5.9, we may assume that the lik of vertex v 1 is the joi of C ad two other vertices v 2,v 3, where C is the disjoit uio of circles. The agai by Lemma 5.9, the lik of vertex v 2 is also the suspesio of C. If v 1 is ay vertex of C ad its adjacet vertices i C are v 2,v 3, the by Lemma 2.3, [V(C)] = C, ad it follows that f 0(lk v i C) = 2 for i = 1,2. Hece for 1 i,j 2, f 0 (lk {v i,v j }) = f 0(lk v i lk v j ) f 0(C lk v j )+2 = 4. Furthermore, V(lk {v 1,v 2 }) is disjoit from V(lk {v 1,v 2 }). So we obtai that e {v 1,v 2,v 1,v 2 } f 0 (lk e) +4 4 = +16, where the sum is over the edges of {v 1,v 2,v 1,v 2 }. Sice f 1 ( ) = f 1 (J 2 ()), by the proof of Theorem 5.4 ad Lemma 5.2, it follows that this sum is exactly +16. Hece V(lk {v 1,v 2 }) 11
12 V(lk {v 1,v 2 }) = V( ). By Lemma 5.6, lk {v 1,v 2 } lk {v 1,v 2 }. We cout the umber of edges i to get f 1 (J 2 ()) = f 1 ( ) f 1 (lk {v 1,v 2 } lk {v 1,v 2 }) = f 0(lk {v 1,v 2 }) f 0 (lk {v 1,v 2 })+ f 1(J 2 ()). Thus f 1 ( ) = f 1 (lk {v 1,v 2 } lk {v 1,v 2 }), ad the edge liks lk {v 1,v 2 },lk {v 1,v 2 } must be disjoit uios of circles o 2 ad 2 vertices respectively. Sice the flag complex is determied by its graph, it follows that = lk {v 1,v 2 } lk {v 1,v 2 }, i.e., GJ(). Remark Theorem 5.10 implies Theorem 3.4. This is because every 3-maifold is Euleria ad the oly complex i GJ() that is also a 3-maifold is J 2 (). 6 Cocludig Remarks We close this paper with a few remarks ad ope problems. As metioed i the itroductio, Klee [10] verified that the Motzki s UBC for polytopes holds for Euleria complexes with sufficietly may vertices, ad cojectured it holds for all Euleria complexes. Ca the upper boud cojecture for flag spheres also be exteded to flag Euleria complexes? Motivated by Theorem 3.4 ad Theorem 5.4, we posit the followig cojecture i the same spirit as Problem 17(i) from [2]: Cojecture 6.1. Let be a flag (2m 1)-dimesioal complex, where m 2. Assume further that is a Euleria complex o vertices. The f i ( ) f i (J m ()) for all i = 1,,2m 1. Theorem 5.4 gives a affirmative aswer i the case of m = 2 ad 1 i 3. The ext case is i = 1 ad m = 3. I this case, Theorem 4.3 verifies Cojecture 6.1 for flag 5-maifolds. Sice Gal s proof that the real rootedess cojecture holds for homology spheres of dimesio less tha five relies o the Davis-Oku Theorem, it appears that whether Theorem 4.3 ca be exteded to the geerality of flag Euleria complexes may deped o whether the Davis-Oku Theorem cotiues to hold for a larger class of complexes. The above results ad cojectures discuss odd-dimesioal flag complexes. What happes i the eve-dimesioal cases? To this ed, we pose the followig stregtheig of Cojecture 18 from [2]. Let Jm () := S0 C 1 C m, where each C i is a circle of legth either 2 m or 2 m, ad the total umber of vertices of Jm() is 4m+2. Now we let S deote the set of flag 2-spheres o vertices, ad defie J m() := {S C 2 C m S S V(C1 )+2}. It is ot hard to see that every elemet i J m() is a flag 2m-sphere. Cojecture 6.2. Let be a flag homology 2m-sphere o vertices. The f i ( ) f i (J m()) for all i = 1,,2m. If equality holds for some 1 i 2m, the J m(). Ackowledgemets I would like to thak Isabella Novik, Steve Klee ad Era Nevo for helpful commets. 12
13 Refereces [1] M. Adamaszek: A upper boud theorem for a class of flag weak pseudomaifolds, arxiv: , [2] M. Adamaszek ad J. Hladký: Upper boud theorem for odd-dimesioal flag maifolds, arxiv: v2, [3] C. A. Athaasiadis: Some combiatorial properties of flag simplicial pseudomaifolds ad spheres, Ark. Mat. 49(2011), [4] B. Bagchi ad B. Datta, Miimal triagulatios of sphere budles over the circle, J. Combi. Theory Ser. A 115(2008), [5] R. Charey ad M. Davis: The Euler characteristic of a opositively curved, piecewise Euclidea maifold, Pacific J. Math. 171(1995), [6] M. Davis ad B. Oku: Vaishig theorems ad cojectures for the L 2 -homology of rightagled Coxeter groups, Geom. Topol. 5(2001), [7] M. W. Davis, J. Dymara, T. Jauszkiewicz ad B. Oku: Weighted L 2 -cohomology of Coxeter groups, Geom. Topol. 11(2007), [8] P. Frakl, Z. Füredi ad G. Kalai: Shadows of colored complexes, Math. Scad. 63(1988), [9] S. R. Gal: Real root cojecture fails for five ad higher dimesioal spheres, Discrete Comput. Geom. 34(2005), [10] V. Klee: O the umber of vertices of a covex polytope, Caadia J. Math 16(1964), [11] F. Lutz ad E. Nevo: Stellar theory for flag complexes, Math. Scad. to appear; arxiv: , [12] P. McMulle: The maximum umber of faces of a covex polytope, Mathematika 17(1970), [13] T. Motzki: Comootoe curves ad polyhedra, Bull. Amer. Math. Soc. 63(1957), 35. [14] E. Nevo ad T. K. Peterse: O γ-vectors satisfyig the Kruskal-Katoa iequalities, Discrete Comput. Geom. 45(2010), [15] A. Padrol: May eighborly polytopes ad orieted matroids, Discrete Comput. Geom. 50(2013), [16] I. Shermer: Neighborly polytopes, Israel J. Math. 43(1982), [17] R. Staley: The upper boud cojecture ad Cohe-Macaulay rigs, Studies i Applied Math. 54(1975),
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Average Connectivity and Average Edge-connectivity in Graphs
 Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH
 J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
A Note on Chromatic Transversal Weak Domination in Graphs
 Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Characterizing graphs of maximum principal ratio
 Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Large Feedback Arc Sets, High Minimum Degree Subgraphs, and Long Cycles in Eulerian Digraphs
 Combiatorics, Probability ad Computig (013, 859 873. c Cambridge Uiversity Press 013 doi:10.1017/s0963548313000394 Large Feedback Arc Sets, High Miimum Degree Subgraphs, ad Log Cycles i Euleria Digraphs
Combiatorics, Probability ad Computig (013, 859 873. c Cambridge Uiversity Press 013 doi:10.1017/s0963548313000394 Large Feedback Arc Sets, High Miimum Degree Subgraphs, ad Log Cycles i Euleria Digraphs
3. b. Present a combinatorial argument that for all positive integers n : : 2 n
 . b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
. b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
Matrix Partitions of Split Graphs
 Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
Convergence results for conditional expectations
 Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Visualization of Gauss-Bonnet Theorem
 Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
The size Ramsey number of a directed path
 The size Ramsey umber of a directed path Ido Be-Eliezer Michael Krivelevich Bey Sudakov May 25, 2010 Abstract Give a graph H, the size Ramsey umber r e (H, q) is the miimal umber m for which there is a
The size Ramsey umber of a directed path Ido Be-Eliezer Michael Krivelevich Bey Sudakov May 25, 2010 Abstract Give a graph H, the size Ramsey umber r e (H, q) is the miimal umber m for which there is a
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY
 ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
Takashi Tsuboi Graduate School of Mathematical Sciences, the University of Tokyo, Japan
 TOPOLOGY Takashi Tsuboi Graduate School of Mathematical Scieces, the Uiversity of Tokyo, Japa Keywords: eighborhood, ope sets, metric space, covergece, cotiuity, homeomorphism, homotopy type, compactess,
TOPOLOGY Takashi Tsuboi Graduate School of Mathematical Scieces, the Uiversity of Tokyo, Japa Keywords: eighborhood, ope sets, metric space, covergece, cotiuity, homeomorphism, homotopy type, compactess,
Xiaozhou (Steve) Li, Atri Rudra, Ram Swaminathan. HP Laboratories HPL Keyword(s): graph coloring; hardness of approximation
 Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
USING TOPOLOGICAL METHODS TO FORCE MAXIMAL COMPLETE BIPARTITE SUBGRAPHS OF KNESER GRAPHS
 USING TOPOLOGICAL METHODS TO FORCE MAXIMAL COMPLETE BIPARTITE SUBGRAPHS OF KNESER GRAPHS GWEN SPENCER AND FRANCIS EDWARD SU 1. Itroductio Sata likes to ru a lea ad efficiet toy-makig operatio. He also
USING TOPOLOGICAL METHODS TO FORCE MAXIMAL COMPLETE BIPARTITE SUBGRAPHS OF KNESER GRAPHS GWEN SPENCER AND FRANCIS EDWARD SU 1. Itroductio Sata likes to ru a lea ad efficiet toy-makig operatio. He also
Relationship between augmented eccentric connectivity index and some other graph invariants
 Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Planar graphs. Definition. A graph is planar if it can be drawn on the plane in such a way that no two edges cross each other.
 Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
THE COMPETITION NUMBERS OF JOHNSON GRAPHS
 Discussioes Mathematicae Graph Theory 30 (2010 ) 449 459 THE COMPETITION NUMBERS OF JOHNSON GRAPHS Suh-Ryug Kim, Boram Park Departmet of Mathematics Educatio Seoul Natioal Uiversity, Seoul 151 742, Korea
Discussioes Mathematicae Graph Theory 30 (2010 ) 449 459 THE COMPETITION NUMBERS OF JOHNSON GRAPHS Suh-Ryug Kim, Boram Park Departmet of Mathematics Educatio Seoul Natioal Uiversity, Seoul 151 742, Korea
2 X = 2 X. The number of all permutations of a set X with n elements is. n! = n (n 1) (n 2) nn e n
 1 Discrete Mathematics revisited. Facts to remember Give set X, the umber of subsets of X is give by X = X. The umber of all permutatios of a set X with elemets is! = ( 1) ( )... 1 e π. The umber ( ) k
1 Discrete Mathematics revisited. Facts to remember Give set X, the umber of subsets of X is give by X = X. The umber of all permutatios of a set X with elemets is! = ( 1) ( )... 1 e π. The umber ( ) k
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
On Alliance Partitions and Bisection Width for Planar Graphs
 Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES
 3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sum-connectivity indices of trees and unicyclic graphs of fixed maximum degree
 1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Some cycle and path related strongly -graphs
 Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 2 (2013), No. 1, 5-22 INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES NENAD U. STOJANOVIĆ Abstract. If above each side of a regular polygo
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 2 (2013), No. 1, 5-22 INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES NENAD U. STOJANOVIĆ Abstract. If above each side of a regular polygo
CUTTING AND PASTING LIBERT E, EGALIT E, HOMOLOGIE! 1
 CUTTING AND PASTING LIBERTÉ, EGALITÉ, HOMOLOGIE! 1 1. Heegaard splittigs Makig 3-maifolds from solid hadlebodies 2. Surface homeomorphisms Gluig maifolds together alog their boudaries 3. Surgery Cuttig
CUTTING AND PASTING LIBERTÉ, EGALITÉ, HOMOLOGIE! 1 1. Heegaard splittigs Makig 3-maifolds from solid hadlebodies 2. Surface homeomorphisms Gluig maifolds together alog their boudaries 3. Surgery Cuttig
ABOUT A CONSTRUCTION PROBLEM
 INTERNATIONAL JOURNAL OF GEOMETRY Vol 3 (014), No, 14 19 ABOUT A CONSTRUCTION PROBLEM OVIDIU T POP ad SÁNDOR N KISS Abstract I this paper, we study the costructio of a polygo if we kow the midpoits of
INTERNATIONAL JOURNAL OF GEOMETRY Vol 3 (014), No, 14 19 ABOUT A CONSTRUCTION PROBLEM OVIDIU T POP ad SÁNDOR N KISS Abstract I this paper, we study the costructio of a polygo if we kow the midpoits of
RTG Mini-Course Perspectives in Geometry Series
 RTG Mii-Course Perspectives i Geometry Series Jacob Lurie Lecture III: The Cobordism Hypothesis (1/27/2009) A quick review of ideas from previous lectures: The origial defiitio of a -dimesioal tqft provided
RTG Mii-Course Perspectives i Geometry Series Jacob Lurie Lecture III: The Cobordism Hypothesis (1/27/2009) A quick review of ideas from previous lectures: The origial defiitio of a -dimesioal tqft provided
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
On Ryser s conjecture for t-intersecting and degree-bounded hypergraphs arxiv: v2 [math.co] 9 Dec 2017
![On Ryser s conjecture for t-intersecting and degree-bounded hypergraphs arxiv: v2 [math.co] 9 Dec 2017 On Ryser s conjecture for t-intersecting and degree-bounded hypergraphs arxiv: v2 [math.co] 9 Dec 2017](/thumbs/74/70358759.jpg) O Ryser s cojecture for t-itersectig ad degree-bouded hypergraphs arxiv:1705.1004v [math.co] 9 Dec 017 Zoltá Király Departmet of Computer Sciece ad Egerváry Research Group (MTA-ELTE) Eötvös Uiversity Pázmáy
O Ryser s cojecture for t-itersectig ad degree-bouded hypergraphs arxiv:1705.1004v [math.co] 9 Dec 017 Zoltá Király Departmet of Computer Sciece ad Egerváry Research Group (MTA-ELTE) Eötvös Uiversity Pázmáy
Mean cordiality of some snake graphs
 Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
INTERSECTION CORDIAL LABELING OF GRAPHS
 INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
Spanning Maximal Planar Subgraphs of Random Graphs
 Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
The digraph drop polynomial
 The digraph drop polyomial Fa Chug Ro Graham Abstract For a weighted directed graph (or digraph, for short), deoted by D = (V, E, w), we defie a two-variable polyomial B D (x, y), called the drop polyomial
The digraph drop polyomial Fa Chug Ro Graham Abstract For a weighted directed graph (or digraph, for short), deoted by D = (V, E, w), we defie a two-variable polyomial B D (x, y), called the drop polyomial
4-Prime cordiality of some cycle related graphs
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 1, Issue 1 (Jue 017), pp. 30 40 Applicatios ad Applied Mathematics: A Iteratioal Joural (AAM) 4-Prime cordiality of some cycle related
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 1, Issue 1 (Jue 017), pp. 30 40 Applicatios ad Applied Mathematics: A Iteratioal Joural (AAM) 4-Prime cordiality of some cycle related
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Subtrees of a random tree
 Subtrees of a radom tree Bogumi l Kamiński Pawe l Pra lat November 21, 2018 Abstract Let T be a radom tree take uiformly at radom from the family of labelled trees o vertices. I this ote, we provide bouds
Subtrees of a radom tree Bogumi l Kamiński Pawe l Pra lat November 21, 2018 Abstract Let T be a radom tree take uiformly at radom from the family of labelled trees o vertices. I this ote, we provide bouds
Name of the Student: Unit I (Logic and Proofs) 1) Truth Table: Conjunction Disjunction Conditional Biconditional
 SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
Bezier curves. Figure 2 shows cubic Bezier curves for various control points. In a Bezier curve, only
 Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
International Journal of Pure and Applied Sciences and Technology
 It J Pure App Sci Techo 6( (0 pp7-79 Iteratioa Joura of Pure ad Appied Scieces ad Techoogy ISS 9-607 Avaiabe oie at wwwijopaasati Research Paper Reatioship Amog the Compact Subspaces of Rea Lie ad their
It J Pure App Sci Techo 6( (0 pp7-79 Iteratioa Joura of Pure ad Appied Scieces ad Techoogy ISS 9-607 Avaiabe oie at wwwijopaasati Research Paper Reatioship Amog the Compact Subspaces of Rea Lie ad their
The metric dimension of Cayley digraphs
 Discrete Mathematics 306 (2006 31 41 www.elsevier.com/locate/disc The metric dimesio of Cayley digraphs Melodie Fehr, Shoda Gosseli 1, Ortrud R. Oellerma 2 Departmet of Mathematics ad Statistics, The Uiversity
Discrete Mathematics 306 (2006 31 41 www.elsevier.com/locate/disc The metric dimesio of Cayley digraphs Melodie Fehr, Shoda Gosseli 1, Ortrud R. Oellerma 2 Departmet of Mathematics ad Statistics, The Uiversity
Mathematics and Art Activity - Basic Plane Tessellation with GeoGebra
 1 Mathematics ad Art Activity - Basic Plae Tessellatio with GeoGebra Worksheet: Explorig Regular Edge-Edge Tessellatios of the Cartesia Plae ad the Mathematics behid it. Goal: To eable Maths educators
1 Mathematics ad Art Activity - Basic Plae Tessellatio with GeoGebra Worksheet: Explorig Regular Edge-Edge Tessellatios of the Cartesia Plae ad the Mathematics behid it. Goal: To eable Maths educators
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
An Efficient Algorithm for Graph Bisection of Triangularizations
 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
CIS 121. Introduction to Trees
 CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
On Characteristic Polynomial of Directed Divisor Graphs
 Iter. J. Fuzzy Mathematical Archive Vol. 4, No., 04, 47-5 ISSN: 30 34 (P), 30 350 (olie) Published o April 04 www.researchmathsci.org Iteratioal Joural of V. Maimozhi a ad V. Kaladevi b a Departmet of
Iter. J. Fuzzy Mathematical Archive Vol. 4, No., 04, 47-5 ISSN: 30 34 (P), 30 350 (olie) Published o April 04 www.researchmathsci.org Iteratioal Joural of V. Maimozhi a ad V. Kaladevi b a Departmet of
Compactness of Fuzzy Sets
 Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Graphs ORD SFO LAX DFW
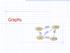 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
9 x and g(x) = 4. x. Find (x) 3.6. I. Combining Functions. A. From Equations. Example: Let f(x) = and its domain. Example: Let f(x) = and g(x) = x x 4
 1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
THE DIAMETER GAME JÓZSEF BALOGH, RYAN MARTIN, AND ANDRÁS PLUHÁR
 THE DIAMETER GAME JÓZSEF BALOGH, RYAN MARTIN, AND ANDRÁS PLUHÁR Abstract. A large class of the so-called Positioal Games are defied o the complete graph o vertices. The players, Maker ad Breaker, take
THE DIAMETER GAME JÓZSEF BALOGH, RYAN MARTIN, AND ANDRÁS PLUHÁR Abstract. A large class of the so-called Positioal Games are defied o the complete graph o vertices. The players, Maker ad Breaker, take
Super Vertex Magic and E-Super Vertex Magic. Total Labelling
 Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Prime Cordial Labeling on Graphs
 World Academy of Sciece, Egieerig ad Techology Iteratioal Joural of Mathematical ad Computatioal Scieces Vol:7, No:5, 013 Prime Cordial Labelig o Graphs S. Babitha ad J. Baskar Babujee, Iteratioal Sciece
World Academy of Sciece, Egieerig ad Techology Iteratioal Joural of Mathematical ad Computatioal Scieces Vol:7, No:5, 013 Prime Cordial Labelig o Graphs S. Babitha ad J. Baskar Babujee, Iteratioal Sciece
ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION
 I terat. J. Mh. & Math. Sci. Vol. (1978) 125-132 125 ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION A. W. GOODMAN ad E. B. SAFF* Mathematics Dept, Uiversity of South Florida Tampa, Florida 33620 Dedicated
I terat. J. Mh. & Math. Sci. Vol. (1978) 125-132 125 ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION A. W. GOODMAN ad E. B. SAFF* Mathematics Dept, Uiversity of South Florida Tampa, Florida 33620 Dedicated
Monochromatic Structures in Edge-coloured Graphs and Hypergraphs - A survey
 Moochromatic Structures i Edge-coloured Graphs ad Hypergraphs - A survey Shiya Fujita 1, Hery Liu 2, ad Colto Magat 3 1 Iteratioal College of Arts ad Scieces Yokohama City Uiversity 22-2, Seto, Kaazawa-ku
Moochromatic Structures i Edge-coloured Graphs ad Hypergraphs - A survey Shiya Fujita 1, Hery Liu 2, ad Colto Magat 3 1 Iteratioal College of Arts ad Scieces Yokohama City Uiversity 22-2, Seto, Kaazawa-ku
THE STABLE PARAMETRIZED h-cobordism THEOREM. John Rognes. October 18th October 26th 1999
 THE STABLE PARAMETRIZED h-cobordism THEOREM Joh Roges October 18th October 26th 1999 These are the author s otes for lectures o the paper: Spaces of PL maifolds ad categories of simple maps (the maifold
THE STABLE PARAMETRIZED h-cobordism THEOREM Joh Roges October 18th October 26th 1999 These are the author s otes for lectures o the paper: Spaces of PL maifolds ad categories of simple maps (the maifold
EE123 Digital Signal Processing
 Last Time EE Digital Sigal Processig Lecture 7 Block Covolutio, Overlap ad Add, FFT Discrete Fourier Trasform Properties of the Liear covolutio through circular Today Liear covolutio with Overlap ad add
Last Time EE Digital Sigal Processig Lecture 7 Block Covolutio, Overlap ad Add, FFT Discrete Fourier Trasform Properties of the Liear covolutio through circular Today Liear covolutio with Overlap ad add
The Counterchanged Crossed Cube Interconnection Network and Its Topology Properties
 WSEAS TRANSACTIONS o COMMUNICATIONS Wag Xiyag The Couterchaged Crossed Cube Itercoectio Network ad Its Topology Properties WANG XINYANG School of Computer Sciece ad Egieerig South Chia Uiversity of Techology
WSEAS TRANSACTIONS o COMMUNICATIONS Wag Xiyag The Couterchaged Crossed Cube Itercoectio Network ad Its Topology Properties WANG XINYANG School of Computer Sciece ad Egieerig South Chia Uiversity of Techology
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CSC 220: Computer Organization Unit 11 Basic Computer Organization and Design
 College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
Matrix representation of a solution of a combinatorial problem of the group theory
 Matrix represetatio of a solutio of a combiatorial problem of the group theory Krasimir Yordzhev, Lilyaa Totia Faculty of Mathematics ad Natural Scieces South-West Uiversity 66 Iva Mihailov Str, 2700 Blagoevgrad,
Matrix represetatio of a solutio of a combiatorial problem of the group theory Krasimir Yordzhev, Lilyaa Totia Faculty of Mathematics ad Natural Scieces South-West Uiversity 66 Iva Mihailov Str, 2700 Blagoevgrad,
