THE ENTIRE FACE IRREGULARITY STRENGTH OF A BOOK WITH POLYGONAL PAGES NILAI KETAKTERATURAN SELURUH MUKA GRAF BUKU SEGI BANYAK
|
|
|
- Marybeth Hubbard
- 6 years ago
- Views:
Transcription
1 Jural Ilmu Matematika da Terapa Desember 015 Volume 9 Nomor Hal THE ENTIRE FACE IRREGULARITY STRENGTH OF A BOOK WITH POLYGONAL PAGES Meili I. Tilukay 1, Ve Y. I. Ilwaru 1, Jurusa Matematika FMIPA Uiversitas Pattimura Jl. Ir. M. Putuhea, Kampus Upatti, Poka-Ambo, Idoesia 1 meili.tilukay@fmipa.upatti.ac.id Abstract A face irregular etire labelig is itroduced by Baca et al. recetly, as a modificatio of the well-kow vertex irregular ad edge irregular total labelig of graphs ad the idea of the etire colourig of plae graph. A face irregular etire k-labelig λ: V E F {1,,, k} of a -coected plae graph G = (V, E, F) is a labelig of vertices, edges, ad faces of G such that for ay two differet faces f ad g, their weights w λ (f) ad w λ (f) are distict. The miimum k for which a plae graph G has a face irregular etire k-labelig is called the etire face irregularity stregth of G, deoted by efs(g). This paper deals with the etire face irregularity stregth of a book with m -polygoal pages, where embedded i a plae as a closed book with sided exteral face. Keywords ad phrases: Book, etire face irregularity stregth, face irregular etire k-labelig, plae graph, polygoal page. NILAI KETAKTERATURAN SELURUH MUKA GRAF BUKU SEGI BANYAK Abstrak Pelabela tak teratur seluruh muka diperkealka oleh Baca et al. baru-baru ii, sebagai suatu modifikasi atas pelabela total tak teratur titik da tak teratur sisi suatu graf serta ide tetag pewaraa legkap pada graf bidag. Pelabela k- tak teratur seluruh muka λ: V E F {1,,, k} dari suatu graf bidag -coected G = (V, E, F) adalah suatu pelabela seluruh titik, sisi, da muka iteral dari G sedemikia sehigga utuk sebarag dua muka f ad g berbeda, bobot muka w λ (f) ad w λ (f) juga berbeda. Bilaga bulat terkecil k sedemikia sehigga suatu graf bidag G memiliki suatu pelabela k-tak teratur seluruh muka disebut ilai ketakteratura seluruh muka dari G, diotasika oleh efs(g). Kami meetuka ilai eksak dari ilai ketakteratura seluruh muka graf buku segi-, dimaa pada bidag datar dapat digambarka seperti suatu buku tertutup. Kata Kuci: Graf bidag, graf buku segi-, ilai ketakteratura seluruh muka, pelabela legkap k-tak teratur muka. 1. Itroductio Let G be a fiite, simple, udirected graph with vertex set V(G)ad edge set E(G). A total labelig of G is a mappig that seds V E to a set of umbers (usually positive or oegative itegers). Accordig to the coditio defied i a total labelig, there are may types of total labelig have bee ivestigated. Baca, Jedrol, Miller, ad Rya i [1] itroduced a vertex irregular ad edge irregular total labelig of graphs. For ay total labelig f: V E {1,,, k}, the weight of a vertex v ad the weight of a edge e = xy are defied by w(v) = f(v) + uv E f(uv) ad w(xy) = f(x) + f(y) + f(xy), respectively. If all the vertex weights are distict, the f is called a vertex irregular total k-labelig, ad if all the edge weights are distict, the f is called a edge irregular total k-labelig. The miimum value of k for which there exist a vertex (a edge) irregular total labelig f: V E {1,,, k} is called the total vertex (edge) irregularity 103
2 104 Tilukay & Ilwaru The Etire Face Irregularity Stregth of a Book with Polygoal Pages stregth of G ad is deoted by tvs(g) (tes(g)), respectively. There are several bouds ad exact values of tvs ad tes were determied for differet types of graphs give i [1] ad listed i []. Furthermore, Ivaco ad Jedrol i [3] posed a cojecture that for arbitrary graph G differet from K 5 ad maximum degree (G), tes(g) = max { E(G) +, (G) + 1 }. 3 Combiig previous coditios o irregular total labelig, Marzuki et al. [4] defied a totally irregular total labelig. A total k-labelig f: V E {1,,, k} of G is called a totally irregular total k-labelig if for ay pair of vertices x ad y, their weights w(x) ad w(y) are distict ad for ay pair of edges x 1 x ad y 1 y, their weights w(x 1 x ) ad w(y 1 y ) are distict. The miimum k for which a graph G has totally irregular total labelig, is called total irregularity stregth of G, deoted by ts(g). They have proved that for every graph G, ts(g) max{tes(g), tvs(g)} (6) Several upper bouds ad exact values of ts were determied for differet types of graphs give i [4], [5], [6], ad [7]. Motivated by this graphs ivariats, Baca et al. i [8] studied irregular labelig of a plae graph by labelig vertices, edges, ad faces the cosiderig the weights of faces. They defied a face irregular etire labelig. A -coected plae graph G = (V, E, F) is a particular drawig of plaar graph o the Euclidea plae where every face is boud by a cycle.. Let G = (V, E, F) be a plae graph. A labelig λ V E F {1,,, k} is called a face irregular etire k-labelig of the plae graph G if for ay two distict faces f ad g of G, their weights w λ (f) ad w λ (f) are distict. The miimum k for which a plae graph G has a face irregular etire k-labelig is called the etire face irregularity stregth of G, deoted by efs(g). The weight of a face f uder the labelig λ is the sum of labels carried by that face ad the edges ad vertices of its boudary. They also provided the boudaries of efs(g). Teorema A. Let G = (V, E, F) be a -coected plae graph G with i i-sided faces, i 3. Let a = mi{i i 0} ad b = max{i i 0}. The a b efs(g) max{ b + 1 i 3 i b}. For b = 1, they gave the lower boud as follow Teorema B. Let G = (V, E, F) be a -coected plae graph G with i i-sided faces, i 3. Let a = mi{i i 0}, b = max{i i 0}, b = 1 ad c = max{i i 0, i < b}. The a + F 1 efs(g). c + 1 Moreover, by cosiderig the maximum degree of a -coected plae graph G, they obtaied the followig theorem. Theorem C. Let G = (V, E, F) be a -coected plae graph G with maximum degree. Let x be a vertex of degree ad let the smallest (ad biggest) face icidet with x be a a-sided (ad a b-sided) face, respectively. The efs(g) a + 1. b They proved that Theorem B is tight for Ladder graph L, 3, ad its variatio ad Theorem C is tight for wheel graph W, 3. I this paper, we determie the exact value of efs of a book with m -polygoal pages which is greater tha the lower boud give i Theorem A - C.
3 Barekeg: Jural Ilmu Matematika da Terapa Desember 015 Volume 9 Nomor Hal Mai Results Cosiderig Theorem C, efs(w ), ad a coditio where every face of a plae graph shares commo vertices or edges, our first result provide a lower boud of the etire face irregularity stregth of a graph with this coditio. This ca be cosidered as geeralizatio of Theorem A, B, ad C. Lemma.1. Let G = (V, E, F) be a -coected plae graph with i i-sided faces, i 3. Let a = mi{i i 0}, b = max{i i 0}, c = max{i i 0, i < b}, ad d be the umber of commo labels of vertices ad edges which have bouded every face of G. The a + F d 1, for c d + 1 b = 1, efs(g) a + F d { b d + 1, otherwise. Proof. Let λ V E F {1,,, k} be a face irregular etire k-labelig of -coected plae graph G = (V, E, F) with efs(g) = k. Our first proof is for b 1. By Theorem A, the miimum face-weight is at least a + 1 ad the maximum face-weight is at least a + F. Sice G is -coected, each face of G is a cycle. It implies that every face might be bouded by commo vertices ad edges. Let d be the umber of commo labels of vertices ad edges which have bouded every face of G ad D be the sum of all commo labels. The the face-weights w λ (f 1 ), w λ (f 1 ),, w λ (f F ) are all distict ad each of them cotais D, implies the variatio of face-weights is deped o a d + i b d + 1 labels. Without addig D, the maximum sum of a face label ad all vertices ad edges-labels surroudig it is at least a + F d. This is the sum of at most b d + 1 labels. Thus, we have efs(g) a+ F d b d+1. For b = 1, it is a direct cosequece from Theorem B with the same reaso as i the result above. This lower boud is tight for ladder graphs ad its variatio ad wheels give i [8]. A book with m -polygoal pages B m, m 1, 3, is a plae graph obtaied from m-copies of cycle C that share a commo edge. There are may ways drawig B m for which the exteral face of B m ca be a -sided face or a ( )-sided face. By cosiderig that topologically, B m ca be draw o a plae as a closed book such that B m has a -sided exteral face, a -sided iteral face, ad m 1 umber of ( )-sided iteral faces, the etire face irregularity stregth of B m is provided i the ext theorem. Theorem.. For B m, m 1, 3, be a book with m -polygoal pages whose a -sided exteral face, a -sided iteral face, ad m 1 ( )-sided iteral faces, we have, for m {1, }; efs(b m ) = { 4 + m 7 4 5, otherwise. Proof. Let B m, m 1, 3, be a -coected plae graph. For m {1, }, by Lemma.1, we have efs(b m ). Labelig the -sided exteral face by label ad all the rests by label 1, the all face-weights are distict. Thus, efs(b m ) =. Now for m >, let z = efs(b m ). Sice every iteral face of B m shares commo vertices, a =, b =, ad b > 1, by Lemma.1, we have z a+ F = b 1 +m 1. Cosider that z = +m 1 is ot valid, sice for m 4, the maximum label is 1. Moreover, sice B m has at least face-weights which are cotributed by the same umber of labels, there must be faces of the same weight. The the divisor must be at least 4 4. Thus we have z 4+m
4 106 Tilukay & Ilwaru The Etire Face Irregularity Stregth of a Book with Polygoal Pages Next, to show that z is a upper boud for etire face irregularity stregth of B m, let B m, m 1, 3, be the -coected plae graph with a -sided iteral face f it, m 1 ( )-sided iteral faces ad a exteral -sided face f ext. Let m 1 = m ad m = m m 1. Our goal is to have m 1 distict eve face-weights ad m distict odd face-weights such that m ( )-sided face-weights are distict ad form a arithmetic progressio. Let z = 4+m 7. It ca be see that B 4 5 m has m differet paths of legth ( 1). Next, we divide m 1 paths parts, where part s-th cosists of (4 5) paths, for 1 s S 1, ad part S-th cosists of ito S = m r 1 = m 1 (S 1)(4 5) paths. Also, we divide m paths ito T = m +1 parts, where the first part 4 5 cosists of (4 6) paths, part t-th cosists of (4 5) paths, for t T 1, ad part T-th cosists of r = m (T 1)(4 5) paths. Let V(B m ) = {x, y, u(s) i j, u(s) k j, v(t) i j v(1) 1 j, v(t) l j 1 s S 1, 1 t T 1, 1 i 4 5, 1 j, 1 k r 1, 1 l r }; E(B m ) = {xy} {u(s) i 1 = x u(s) i, u(s) i j 1 = u(s) i j u(s) i j, u(s) i 3 = u(s) i 4 y 1 s S 1, 1 i 4 5, j } {u(s) i 1 = x u(s) i, u(s) i j 1 = u(s) i j u(s) i j, u(s) i 3 = u(s) i 4 y 1 i r 1, j } {v(t) i 1 = xv(t) i, v(t) i j 1 = v(t) i j v(t) i j, v(t) i 3 = v(t) i 4 y 1 t T, 1 i 4 5, j } {v(t) i 1 = xv(t) i, v(t) i j 1 = v(t) i j v(t) i j, v(t) i 3 = v(t) i 4 y 1 i r, j }; F(B m ) = {f ext, f it, u(s) i, u(s) k, v(t) i v(1) 1, v(t) j 1 s S 1, 1 t T 1, 1 i 4 5, 1 k r 1, 1 l r }; Where f ext is bouded by cycle xv(1) v(1) 4 v(1) 4 yx; f it is bouded by cycle xu(1) 1 u(1) 1 4 u(1) 1 4 yx; u(s) i is bouded by cycle xu(s) i u(s) 4 i u(s) 4 i yu(s) 4 i+1 u(s) 6 i+1 u(s) i+1 x, for 1 s S, i r 1 ; u(s) r1 is bouded by cycle xu(s) r1 u(s) 4 r1 u(s) 4 r1 yv(t) 4 r v(t) 6 r v(t) r x; ad v(t) i is bouded by cycle xv(t) i v(t) 4 i v(t) 4 i yv(t) 4 i+1 v(t) 6 i+1 v(t) i+1 x, for 1 t T, i r ; Our otatios above imply that, without losig geerality, for v(t) i j, we let i 4 5 for t = 1. It meas that there is o vertex or edge or face v(1) 1 j. Now, we divide our labelig of B m ito cases as follows: Case 1. For odd m with r 1 or eve m; Defie a etire k-labelig λ V E F {1,,, k} of B m as follows. λ(x) = λ(y) = λ(xy) = λ(f ext ) = 1; λ(f it ) = ;
5 Barekeg: Jural Ilmu Matematika da Terapa Desember 015 Volume 9 Nomor Hal λ(u(s) i j ) = λ (v(t) i j ) = s 1 for 1 s S, 1 i mi{r 1, } ad 1 j i 1 s for 1 s S, 1 i mi{r 1, } ad i j s for 1 s S, 1 i mi{r 1, 4 5} ad 1 j i + { s + 1 for 1 s S, 1 i mi{r 1, 4 5} ad i + 1 j t 1, for 1 t T, 1 i mi{r, } ad 1 j i ; t, for 1 t T, 1 i mi{r, } ad i 1 j 3; t, for 1 t T, 1 i mi{r, 4 5} ad 1 j i + 3; t + 1, for 1 t T, 1 i mi{r, 4 5} ad i + j 3; t, for 1 t T, i = 1 ad j = ; t 1, for 1 t T, i mi{r, 1} ad j = ; t, for 1 t T 1, i 4 5 ad j =. { t, for t = T, 1 i mi{r 1, 4 6} ad j = Case. For odd m with r = 1 or r 4 5; Defie a etire k-labelig λ V E F {1,,, k} of B m as follows. λ (x) = λ (y) = λ (xy) = λ (f ext ) = 1; λ (f it ) = ; λ (u(s) i j ) = λ(u(s) i j ) λ (v(t) i j ) = T, for r = 1, t = T, i = 1, j = 1; T 1, for r = 1, t = T 1, i = 4 5, j = ; λ(v(t) i j ) + 1, for r odd, r 4 5, t = T, i = r, j = 1; λ(v(t) i j ) 1, for r odd, r 4 5, t = T, i = r 1, j = ; λ(v(t) i j ) 1, for r eve, r 4 5, t = T, i = r 1, j = 3; λ(v(t) i j ) + 1, for r eve, r 4 5, t = T, i = r 1, j = ; { λ(v(t) j i ), for otherwise. It is easy to check that the labelig λ is a etire z-labelig. The we have evaluate the face weights set {w(f ext ), w(f it ), w(u(s) i ), w(v(t) i ) 1 s S, 1 t T, 1 i 4 5} as follows. w(f ext ) = + 1; w(f it ) = + ; (s 1)(4 5) + i, for 1 s S 1, 1 i 4 5; w(u(s) (s 1)(4 5) + i, for s = S 1, 1 i r i ) = 1 ; (s 1)(4 5) + r 1, for eve m, s = S 1, i = r 1 ; { (s 1)(4 5) + r 1 1, for odd m, s = S 1, i = r 1. w(v(t) (t 1)(4 5) + i + 1, for 1 t T 1, 1 i 4 5; i ) = { (T 1)(4 5) + i + 1, for t = T, 1 i r 1. Sice all face-weights are distict, the λ is a face irregular etire z-labelig of B m where m is odd with r 1 or m is eve; ad λ is a face irregular etire z-labelig of B m where m is odd with r = 1 or r 4 5. Thus, z = 4+m 7 is the etire face irregularity stregth of B 4 5 m. Note that our result i Theorem. show that the efs(b m ) is greater tha the lower boud i Lemma.1. Hece, we propose the followig ope problem.
6 108 Tilukay & Ilwaru The Etire Face Irregularity Stregth of a Book with Polygoal Pages Ope Problems 1. Fid a class of graph which satisfy a coditio where the lower boud i Lemma.1 is sharp;. Geeralize the lower boud for ay coditio. Refereces [1] M. Baca, S. Jedrol, M. Miller ad J. Rya, O Irregular Total Labeligs, Discrete Mathematics, vol. 307, pp , 007. [] J. A. Galia, A Dyamic Survey of Graph Labelig, Electroic Joural of Combiatorics, vol. 18 #DS6, 015. [3] J. Ivaco ad S. Jedrol, The Total Edge Irregularity Stregth of Trees, Discuss. Math. Graph Theory, vol. 6, pp , 006. [4] C. C. Marzuki, A. N. M. Salma ad M. Miller, O The Total Irregularity Stregths of Cycles ad Paths, Far East Joural of Mathematical Scieces, vol. 8 (1), pp. 1-1, 013. [5] R. Ramdai ad A. N. M. Salma, O The Total Irregularity Stregths of Some Cartesia Products Graphs, AKCE It. J. Graphs Comb., vol. 10 No., pp , 013. [6] R. Ramdai, A. N. M. Salma, H. Assiyatu, A. Semaicova-Feovcikova ad M. Baca, Total Irregularity Stregth of Three Family of Graphs, Math. Comput. Sci, vol. 9, pp. 9-37, 015. [7] M. I. Tilukay, A. N. M. Salma ad E. R. Persulessy, "O The Total Irregularity Stregth of Fa, Wheel, Triagular Book, ad Friedship Graphs," Procedia Computer Sciece, vol. 74, pp , 015. [8] M. Baca, S. Jedrol, K. Kathiresa ad K. Muthugurupackiam, Etire Labelig of Plae Graphs, Applied Mathematics ad Iformatio Scieces, vol. 9, o. 1, pp , 015.
Mean cordiality of some snake graphs
 Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
INTERSECTION CORDIAL LABELING OF GRAPHS
 INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Super Vertex Magic and E-Super Vertex Magic. Total Labelling
 Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Some cycle and path related strongly -graphs
 Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Australian Journal of Basic and Applied Sciences, 5(11): , 2011 ISSN On tvs of Subdivision of Star S n
 Australia Joural of Basic ad Applied Scieces 5(11): 16-156 011 ISSN 1991-8178 O tvs of Subdivisio of Star S 1 Muhaad Kara Siddiqui ad Deeba Afzal 1 Abdus Sala School of Matheatical Scieces G.C. Uiversity
Australia Joural of Basic ad Applied Scieces 5(11): 16-156 011 ISSN 1991-8178 O tvs of Subdivisio of Star S 1 Muhaad Kara Siddiqui ad Deeba Afzal 1 Abdus Sala School of Matheatical Scieces G.C. Uiversity
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
4-PRIME CORDIAL LABELING OF SOME DEGREE SPLITTING GRAPHS
 Iteratioal Joural of Maagemet, IT & Egieerig Vol. 8 Issue 7, July 018, ISSN: 49-0558 Impact Factor: 7.119 Joural Homepage: Double-Blid Peer Reviewed Refereed Ope Access Iteratioal Joural - Icluded i the
Iteratioal Joural of Maagemet, IT & Egieerig Vol. 8 Issue 7, July 018, ISSN: 49-0558 Impact Factor: 7.119 Joural Homepage: Double-Blid Peer Reviewed Refereed Ope Access Iteratioal Joural - Icluded i the
ON THE TOTAL VERTEX IRREGULARITY STRENGTHS OF QUADTREES AND BANANA TREES
 J. Indones. Math. Soc. Vol. 18, No. 1 (2012), pp. 31 36. ON THE TOTAL VERTEX IRREGULARITY STRENGTHS OF QUADTREES AND BANANA TREES Nurdin Department of Mathematics, Faculty of Mathematics and Natural Sciences,
J. Indones. Math. Soc. Vol. 18, No. 1 (2012), pp. 31 36. ON THE TOTAL VERTEX IRREGULARITY STRENGTHS OF QUADTREES AND BANANA TREES Nurdin Department of Mathematics, Faculty of Mathematics and Natural Sciences,
Relationship between augmented eccentric connectivity index and some other graph invariants
 Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
EVEN VERTEX EQUITABLE EVEN LABELING FOR CYCLE RELATED GRAPHS
 Kragujevac Joural of Matheatics Volue 43(3) (019), Pages 47 441. EVEN VERTEX EQUITABLE EVEN LABELING FOR CYCLE RELATED GRAPHS A. LOURDUSAMY 1 AND F. PATRICK 1 Abstract. Let G be a graph with p vertices
Kragujevac Joural of Matheatics Volue 43(3) (019), Pages 47 441. EVEN VERTEX EQUITABLE EVEN LABELING FOR CYCLE RELATED GRAPHS A. LOURDUSAMY 1 AND F. PATRICK 1 Abstract. Let G be a graph with p vertices
A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH
 J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
4-Prime cordiality of some cycle related graphs
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 1, Issue 1 (Jue 017), pp. 30 40 Applicatios ad Applied Mathematics: A Iteratioal Joural (AAM) 4-Prime cordiality of some cycle related
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 1, Issue 1 (Jue 017), pp. 30 40 Applicatios ad Applied Mathematics: A Iteratioal Joural (AAM) 4-Prime cordiality of some cycle related
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
A Note on Chromatic Transversal Weak Domination in Graphs
 Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Sum-connectivity indices of trees and unicyclic graphs of fixed maximum degree
 1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
MINIMUM COVERING SEIDEL ENERGY OF A GRAPH
 J. Idoes. Math. Soc. Vol., No. 1 (016, pp. 71 8. MINIMUM COVERING SEIDEL ENERGY OF A GRAPH M. R. Rajesh Kaa 1, R. Jagadeesh, Mohammad Reza Farahai 3 1 Post Graduate Departmet of Mathematics, Maharai s
J. Idoes. Math. Soc. Vol., No. 1 (016, pp. 71 8. MINIMUM COVERING SEIDEL ENERGY OF A GRAPH M. R. Rajesh Kaa 1, R. Jagadeesh, Mohammad Reza Farahai 3 1 Post Graduate Departmet of Mathematics, Maharai s
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
Some New Results on Prime Graphs
 Ope Joural of Discrete Mathematics, 202, 2, 99-04 http://dxdoiorg/0426/ojdm202209 Published Olie July 202 (http://wwwscirporg/joural/ojdm) Some New Results o Prime Graphs Samir Vaidya, Udaya M Prajapati
Ope Joural of Discrete Mathematics, 202, 2, 99-04 http://dxdoiorg/0426/ojdm202209 Published Olie July 202 (http://wwwscirporg/joural/ojdm) Some New Results o Prime Graphs Samir Vaidya, Udaya M Prajapati
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY
 ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
The Platonic solids The five regular polyhedra
 The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Force Network Analysis using Complementary Energy
 orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
Prime Cordial Labeling on Graphs
 World Academy of Sciece, Egieerig ad Techology Iteratioal Joural of Mathematical ad Computatioal Scieces Vol:7, No:5, 013 Prime Cordial Labelig o Graphs S. Babitha ad J. Baskar Babujee, Iteratioal Sciece
World Academy of Sciece, Egieerig ad Techology Iteratioal Joural of Mathematical ad Computatioal Scieces Vol:7, No:5, 013 Prime Cordial Labelig o Graphs S. Babitha ad J. Baskar Babujee, Iteratioal Sciece
Average Connectivity and Average Edge-connectivity in Graphs
 Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Syddansk Universitet. The total irregularity of a graph. Abdo, H.; Brandt, S.; Dimitrov, D.
 Syddask Uiversitet The total irregularity of a graph Abdo, H.; Bradt, S.; Dimitrov, D. Published i: Discrete Mathematics & Theoretical Computer Sciece Publicatio date: 014 Documet versio Publisher's PDF,
Syddask Uiversitet The total irregularity of a graph Abdo, H.; Bradt, S.; Dimitrov, D. Published i: Discrete Mathematics & Theoretical Computer Sciece Publicatio date: 014 Documet versio Publisher's PDF,
Characterizing graphs of maximum principal ratio
 Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
THE COMPETITION NUMBERS OF JOHNSON GRAPHS
 Discussioes Mathematicae Graph Theory 30 (2010 ) 449 459 THE COMPETITION NUMBERS OF JOHNSON GRAPHS Suh-Ryug Kim, Boram Park Departmet of Mathematics Educatio Seoul Natioal Uiversity, Seoul 151 742, Korea
Discussioes Mathematicae Graph Theory 30 (2010 ) 449 459 THE COMPETITION NUMBERS OF JOHNSON GRAPHS Suh-Ryug Kim, Boram Park Departmet of Mathematics Educatio Seoul Natioal Uiversity, Seoul 151 742, Korea
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
ABOUT A CONSTRUCTION PROBLEM
 INTERNATIONAL JOURNAL OF GEOMETRY Vol 3 (014), No, 14 19 ABOUT A CONSTRUCTION PROBLEM OVIDIU T POP ad SÁNDOR N KISS Abstract I this paper, we study the costructio of a polygo if we kow the midpoits of
INTERNATIONAL JOURNAL OF GEOMETRY Vol 3 (014), No, 14 19 ABOUT A CONSTRUCTION PROBLEM OVIDIU T POP ad SÁNDOR N KISS Abstract I this paper, we study the costructio of a polygo if we kow the midpoits of
Hamiltonian-T*- Laceability in Jump Graphs Of Diameter Two
 IOSR Jourl of Mthemtics IOSR-JM e-issn 78-78 p-issn9-76x. Volume Issue Ver. III My-Ju. PP -6 www.iosrjourls.org Hmiltoi-T*- Lcebility i Jump Grphs Of Dimeter Two Mjuth.G Murli.R Deprtmet of MthemticsGopl
IOSR Jourl of Mthemtics IOSR-JM e-issn 78-78 p-issn9-76x. Volume Issue Ver. III My-Ju. PP -6 www.iosrjourls.org Hmiltoi-T*- Lcebility i Jump Grphs Of Dimeter Two Mjuth.G Murli.R Deprtmet of MthemticsGopl
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
Mathematics and Art Activity - Basic Plane Tessellation with GeoGebra
 1 Mathematics ad Art Activity - Basic Plae Tessellatio with GeoGebra Worksheet: Explorig Regular Edge-Edge Tessellatios of the Cartesia Plae ad the Mathematics behid it. Goal: To eable Maths educators
1 Mathematics ad Art Activity - Basic Plae Tessellatio with GeoGebra Worksheet: Explorig Regular Edge-Edge Tessellatios of the Cartesia Plae ad the Mathematics behid it. Goal: To eable Maths educators
The Counterchanged Crossed Cube Interconnection Network and Its Topology Properties
 WSEAS TRANSACTIONS o COMMUNICATIONS Wag Xiyag The Couterchaged Crossed Cube Itercoectio Network ad Its Topology Properties WANG XINYANG School of Computer Sciece ad Egieerig South Chia Uiversity of Techology
WSEAS TRANSACTIONS o COMMUNICATIONS Wag Xiyag The Couterchaged Crossed Cube Itercoectio Network ad Its Topology Properties WANG XINYANG School of Computer Sciece ad Egieerig South Chia Uiversity of Techology
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Computing Vertex PI, Omega and Sadhana Polynomials of F 12(2n+1) Fullerenes
 Iraia Joural of Mathematical Chemistry, Vol. 1, No. 1, April 010, pp. 105 110 IJMC Computig Vertex PI, Omega ad Sadhaa Polyomials of F 1(+1) Fullerees MODJTABA GHORBANI Departmet of Mathematics, Faculty
Iraia Joural of Mathematical Chemistry, Vol. 1, No. 1, April 010, pp. 105 110 IJMC Computig Vertex PI, Omega ad Sadhaa Polyomials of F 1(+1) Fullerees MODJTABA GHORBANI Departmet of Mathematics, Faculty
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
On Characteristic Polynomial of Directed Divisor Graphs
 Iter. J. Fuzzy Mathematical Archive Vol. 4, No., 04, 47-5 ISSN: 30 34 (P), 30 350 (olie) Published o April 04 www.researchmathsci.org Iteratioal Joural of V. Maimozhi a ad V. Kaladevi b a Departmet of
Iter. J. Fuzzy Mathematical Archive Vol. 4, No., 04, 47-5 ISSN: 30 34 (P), 30 350 (olie) Published o April 04 www.researchmathsci.org Iteratioal Joural of V. Maimozhi a ad V. Kaladevi b a Departmet of
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES
 3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Exact Minimum Lower Bound Algorithm for Traveling Salesman Problem
 Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION
 I terat. J. Mh. & Math. Sci. Vol. (1978) 125-132 125 ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION A. W. GOODMAN ad E. B. SAFF* Mathematics Dept, Uiversity of South Florida Tampa, Florida 33620 Dedicated
I terat. J. Mh. & Math. Sci. Vol. (1978) 125-132 125 ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION A. W. GOODMAN ad E. B. SAFF* Mathematics Dept, Uiversity of South Florida Tampa, Florida 33620 Dedicated
Rainbow Vertex Coloring for Line, Middle, Central, Total Graph of Comb Graph
 Idia Joural of Sciece ad Techology, Vol 9(S, DOI: 0.7485/ijst/206/v9iS/97463, December 206 ISSN (Prit : 0974-6846 ISSN (Olie : 0974-5645 Raibow Vertex Colorig for Lie, Middle, Cetral, Total Graph of Comb
Idia Joural of Sciece ad Techology, Vol 9(S, DOI: 0.7485/ijst/206/v9iS/97463, December 206 ISSN (Prit : 0974-6846 ISSN (Olie : 0974-5645 Raibow Vertex Colorig for Lie, Middle, Cetral, Total Graph of Comb
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
On Spectral Theory Of K-n- Arithmetic Mean Idempotent Matrices On Posets
 Iteratioal Joural of Sciece, Egieerig ad echology Research (IJSER), Volume 5, Issue, February 016 O Spectral heory Of -- Arithmetic Mea Idempotet Matrices O Posets 1 Dr N Elumalai, ProfRMaikada, 3 Sythiya
Iteratioal Joural of Sciece, Egieerig ad echology Research (IJSER), Volume 5, Issue, February 016 O Spectral heory Of -- Arithmetic Mea Idempotet Matrices O Posets 1 Dr N Elumalai, ProfRMaikada, 3 Sythiya
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
SOME ALGEBRAIC IDENTITIES IN RINGS AND RINGS WITH INVOLUTION
 Palestie Joural of Mathematics Vol. 607, 38 46 Palestie Polytechic Uiversity-PPU 07 SOME ALGEBRAIC IDENTITIES IN RINGS AND RINGS WITH INVOLUTION Chirag Garg ad R. K. Sharma Commuicated by Ayma Badawi MSC
Palestie Joural of Mathematics Vol. 607, 38 46 Palestie Polytechic Uiversity-PPU 07 SOME ALGEBRAIC IDENTITIES IN RINGS AND RINGS WITH INVOLUTION Chirag Garg ad R. K. Sharma Commuicated by Ayma Badawi MSC
Planar graphs. Definition. A graph is planar if it can be drawn on the plane in such a way that no two edges cross each other.
 Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
Fibonacci and Super Fibonacci Graceful Labeling of Some Graphs*
 Studie i Mathematical Sciece Vol, No, 0, pp 4-35 wwwccaadaorg ISSN 93-8444 [Prit] ISSN 93-845 [Olie] wwwccaadaet iboacci ad Super iboacci Graceful Labelig of Some Graph* SKVaidya, * PLVihol Abtract: I
Studie i Mathematical Sciece Vol, No, 0, pp 4-35 wwwccaadaorg ISSN 93-8444 [Prit] ISSN 93-845 [Olie] wwwccaadaet iboacci ad Super iboacci Graceful Labelig of Some Graph* SKVaidya, * PLVihol Abtract: I
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
International Journal of Pure and Applied Sciences and Technology
 It J Pure App Sci Techo 6( (0 pp7-79 Iteratioa Joura of Pure ad Appied Scieces ad Techoogy ISS 9-607 Avaiabe oie at wwwijopaasati Research Paper Reatioship Amog the Compact Subspaces of Rea Lie ad their
It J Pure App Sci Techo 6( (0 pp7-79 Iteratioa Joura of Pure ad Appied Scieces ad Techoogy ISS 9-607 Avaiabe oie at wwwijopaasati Research Paper Reatioship Amog the Compact Subspaces of Rea Lie ad their
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
arxiv: v2 [cs.ds] 24 Mar 2018
![arxiv: v2 [cs.ds] 24 Mar 2018 arxiv: v2 [cs.ds] 24 Mar 2018](/thumbs/81/83887444.jpg) Similar Elemets ad Metric Labelig o Complete Graphs arxiv:1803.08037v [cs.ds] 4 Mar 018 Pedro F. Felzeszwalb Brow Uiversity Providece, RI, USA pff@brow.edu March 8, 018 We cosider a problem that ivolves
Similar Elemets ad Metric Labelig o Complete Graphs arxiv:1803.08037v [cs.ds] 4 Mar 018 Pedro F. Felzeszwalb Brow Uiversity Providece, RI, USA pff@brow.edu March 8, 018 We cosider a problem that ivolves
Partitions of a Convex Polygon
 HAPTER 6 Partitios of a ovex Polygo 6 INTRODUTION I our survey we have come across some results o eumeratio of ocrossig cofiguratios o the set of vertices of a covex polygo, such as triagulatios ad trees
HAPTER 6 Partitios of a ovex Polygo 6 INTRODUTION I our survey we have come across some results o eumeratio of ocrossig cofiguratios o the set of vertices of a covex polygo, such as triagulatios ad trees
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
Intermediate Statistics
 Gait Learig Guides Itermediate Statistics Data processig & display, Cetral tedecy Author: Raghu M.D. STATISTICS DATA PROCESSING AND DISPLAY Statistics is the study of data or umerical facts of differet
Gait Learig Guides Itermediate Statistics Data processig & display, Cetral tedecy Author: Raghu M.D. STATISTICS DATA PROCESSING AND DISPLAY Statistics is the study of data or umerical facts of differet
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
( n+1 2 ) , position=(7+1)/2 =4,(median is observation #4) Median=10lb
 Chapter 3 Descriptive Measures Measures of Ceter (Cetral Tedecy) These measures will tell us where is the ceter of our data or where most typical value of a data set lies Mode the value that occurs most
Chapter 3 Descriptive Measures Measures of Ceter (Cetral Tedecy) These measures will tell us where is the ceter of our data or where most typical value of a data set lies Mode the value that occurs most
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
Convergence results for conditional expectations
 Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Area As A Limit & Sigma Notation
 Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
Name of the Student: Unit I (Logic and Proofs) 1) Truth Table: Conjunction Disjunction Conditional Biconditional
 SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
How to construct new super edge-magic graphs from some old ones
 How to construct new super edge-magic graphs from some old ones E.T. Baskoro 1, I W. Sudarsana 2 and Y.M. Cholily 1 1 Department of Mathematics Institut Teknologi Bandung (ITB), Jalan Ganesa 10 Bandung
How to construct new super edge-magic graphs from some old ones E.T. Baskoro 1, I W. Sudarsana 2 and Y.M. Cholily 1 1 Department of Mathematics Institut Teknologi Bandung (ITB), Jalan Ganesa 10 Bandung
Visualization of Gauss-Bonnet Theorem
 Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
An Efficient Algorithm for Graph Bisection of Triangularizations
 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
IJESMR International Journal OF Engineering Sciences & Management Research
 [Geetha, (10): October, 015] ISSN 39-6193 Impact Factor (PIF):.3 Iteratioal Joural OF Egieerig Scieces & Maagemet Research CONSTRUCTION OF DIOPHANTINE QUADRUPLES WITH PROPERTY D(A PERFECT SQUARE) V.Geetha
[Geetha, (10): October, 015] ISSN 39-6193 Impact Factor (PIF):.3 Iteratioal Joural OF Egieerig Scieces & Maagemet Research CONSTRUCTION OF DIOPHANTINE QUADRUPLES WITH PROPERTY D(A PERFECT SQUARE) V.Geetha
Graphs ORD SFO LAX DFW
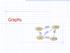 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
BOOLEAN MATHEMATICS: GENERAL THEORY
 CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Fundamentals of Media Processing. Shin'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dinh Le
 Fudametals of Media Processig Shi'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dih Le Today's topics Noparametric Methods Parze Widow k-nearest Neighbor Estimatio Clusterig Techiques k-meas Agglomerative Hierarchical
Fudametals of Media Processig Shi'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dih Le Today's topics Noparametric Methods Parze Widow k-nearest Neighbor Estimatio Clusterig Techiques k-meas Agglomerative Hierarchical
CSC 220: Computer Organization Unit 11 Basic Computer Organization and Design
 College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
arxiv: v1 [math.co] 22 Dec 2015
![arxiv: v1 [math.co] 22 Dec 2015 arxiv: v1 [math.co] 22 Dec 2015](/thumbs/92/109673654.jpg) The flag upper boud theorem for 3- ad 5-maifolds arxiv:1512.06958v1 [math.co] 22 Dec 2015 Hailu Zheg Departmet of Mathematics Uiversity of Washigto Seattle, WA 98195-4350, USA hailuz@math.washigto.edu
The flag upper boud theorem for 3- ad 5-maifolds arxiv:1512.06958v1 [math.co] 22 Dec 2015 Hailu Zheg Departmet of Mathematics Uiversity of Washigto Seattle, WA 98195-4350, USA hailuz@math.washigto.edu
An Efficient Algorithm for Graph Bisection of Triangularizations
 Applied Mathematical Scieces, Vol. 1, 2007, o. 25, 1203-1215 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045, Oe
Applied Mathematical Scieces, Vol. 1, 2007, o. 25, 1203-1215 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045, Oe
PLEASURE TEST SERIES (XI) - 04 By O.P. Gupta (For stuffs on Math, click at theopgupta.com)
 wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
EXTREMAL PROPERTIES OF ZAGREB COINDICES AND DEGREE DISTANCE OF GRAPHS
 Miskolc Mathematical Notes HU e-issn 1787-413 Vol. 11 (010), No., pp. 19 137 ETREMAL PROPERTIES OF ZAGREB COINDICES AND DEGREE DISTANCE OF GRAPHS S. HOSSEIN-ZADEH, A. HAMZEH AND A. R. ASHRAFI Received
Miskolc Mathematical Notes HU e-issn 1787-413 Vol. 11 (010), No., pp. 19 137 ETREMAL PROPERTIES OF ZAGREB COINDICES AND DEGREE DISTANCE OF GRAPHS S. HOSSEIN-ZADEH, A. HAMZEH AND A. R. ASHRAFI Received
Matrix Partitions of Split Graphs
 Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
found that now considerable work has been done in this started with some example, which motivates the later results.
 8 Iteratioal Joural of Comuter Sciece & Emergig Techologies (E-ISSN: 44-64) Volume, Issue 4, December A Study o Adjacecy Matrix for Zero-Divisor Grahs over Fiite Rig of Gaussia Iteger Prajali, Amit Sharma
8 Iteratioal Joural of Comuter Sciece & Emergig Techologies (E-ISSN: 44-64) Volume, Issue 4, December A Study o Adjacecy Matrix for Zero-Divisor Grahs over Fiite Rig of Gaussia Iteger Prajali, Amit Sharma
CIS 121. Introduction to Trees
 CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
Compactness of Fuzzy Sets
 Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Σ P(i) ( depth T (K i ) + 1),
 EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
