Conditional gradient algorithms for machine learning

Transcription

1 Conditional gradient algorithms for machine learning Zaid Harchaoui LEAR-LJK, INRIA Grenoble Anatoli Juditsky LJK, Université de Grenoble Arkadi Nemirovski Georgia Tech Abstract We consider penalized formulations of machine learning problems with regularization penalty having conic structure. For several important learning problems, state-of-the-art optimization approaches such as proximal gradient algorithms are difficult to apply and computationally expensive, preventing from using them for large-scale learning purpose. We present a conditional gradient algorithm, with theoretical guarantees, and show promising experimental results on two largescale real-world datasets. 1 Introduction We consider statistical learning problems that can be framed into convex optimization problems of the form f(x) + λ x min x K where f is a convex function with Lipschitz continuous gradient and K is a closed convex cone of a Euclidean space. This encompasses supervised classification, regression, ranking, etc. with various choices for the regularization penalty including regular l p -norms, as well as more structured regularization penalties such as the group-lasso penalty or the trace-norm [20]. A wealth of convex optimization algorithms was proposed to tackle such problems; see [20] for a recent overview. Among them, the celebrated Nesterov optimal gradient method for smooth and composite minimization [15, 16], and its stochastic approximation counterparts [14], are now state-of-the-art in machine learning. These algorithms enjoy the best possible theoretical complexity estimate. For instance, Nesterov s algorithm reaches a solution with accuracy ɛ in O(D L/ɛ), where L is the Lipschitz constant of the gradient of the smooth component of the objective, and D is the problem-domain parameter in the norm. However, these algorithms work by solving at each iteration a sub-problem which involves the minimization of the sum of a linear form and a distance-generating function on the problem domain. Most often, and this explains the popularity of this family of algorithms in the last decade, exactly solving the sub-problem is computationally cheap [3]. However, in high-dimensional problems such as multi-task learning with a large number of tasks and features, solving this sub-problem is computationally challenging when the trace-norm regularization is used for instance [13, 17]. These limitations recently motivated alternative approaches, which do not require to solve hard sub-problems at each iteration, and triggered a renewed interest in conditional gradient algorithms. The conditional gradient algorithm [8, 6] (a.k.a. Frank-Wolfe algorithms) works by minimizing a linear form on the problem domain at each iteration, a simpler subproblem than the one involved in proximal gradient algorithms; see [12, 18, 19, 7, 11] for recent works. However, the conditional gradient algorithm allows to tackle constrained formulations of learning problems, whereas penalized formulations are more widespread in applications. We propose a new algorithm suitable for penalized formulations, reminiscent of the conditional gradient algorithm, with theoretical guarantees. 1

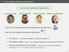
2 Constrained formulation I Penalized formulation Constrained formulation II subject to f(x) x ρ f(x) + λ x subject to x f(x) δ Figure 1: Three main formulations of machine learning optimization problems. 2 Penalized learning formulation We first review three main types of formulations of machine learning problems, then detail our assumptions before we present our approach. Learning formulations Depending on the task at hand, some formulations might be preferable to others to pose the learning problem. Three main formulations of machine learning problems as summarized in Figure 1, where f(x) plays the role of the empirical risk and x the role of the regularization penalty/constraint (see [10] more details). Common wisdom would recommend the formulation where prior knowledge can easily be incorporated. When prior knowledge of the noise level are available, then constrained formulation II is more convenient, as one can directly encode this knowledge in the constraint. Similarly, when prior knowledge or pilot estimates on the learning parameter (weight vector/matrix) is available, then constrained formulation I is more appropriate. Finally, when no prior knowledge is available, its is common to consider the penalized formulation as the most appropriate option. Penalized formulation that is We focus on the penalized formulation of learning problems in this paper, Minimize x K f(x) + λ x (2.1) where K E is a closed convex cone of Euclidean space E. Without loss of generality, we can assume that K linearly spans E. We assume that is a norm on E, and f is a convex function with Lipschitz continuous gradient, that is f (x) f (y) L f x y for all x, y K, where denotes the dual norm dual of. Using that x is also a gauge/minkowski functional γ B (x) = inf{r, x rb} with respect to the unit-ball B = {x E, x 1} [7], we rewrite the problem as Minimize x,r where F ([x; r]) and K + are resp. defined as F ([x; r]) subject to [x; r] K +, (2.2) F ([x; r]) := f(x) + λr and K + := {[x; r], x K, x rb}. We shall use resp. the shorthand notations x = x[x; r] and r = r[x; r] to retrieve resp. the x-part and r-part of [x; r]. Note that the x-part x[x ɛ, r ɛ ] of an ɛ-solution to problem (2.2) is also an ɛ-solution to problem (2.1). 3 Conditional-gradient-type algorithm for penalized learning formulations We now describe the proposed algorithm for solving problem (2.2), which we simply rewrite using z := [x; r] as F (z) subject to z K + (3.3) Being different, the proposed method is closely related to the regular conditional gradient algorithm. Namely, it only requires a kind of linearization oracle in addition to objective and gradient calls. 2

3 Minimization oracle The way the proposed algorithm proceeds is reminiscent of the regular conditional gradient algorithm. Note, however, that the proposed algorithm is not an instance of the traditional conditional gradient algorithm. The conditional gradient algorithm was designed exclusively for constrained formulations of type I (see Figure 2), and only requires a so-called linearization oracle in addition to objective and gradient evaluations. In the regular conditional gradient algorithm, the linearization oracle corresponds to min x X f (x), x where X is a closed convex set. Similarly, in addition to objective and gradient calls 1, the proposed algorithm makes calls to a minimization oracle, which writes as x(g) := argmin g, x, (3.4) x K 1 where K 1 := {x, x K, x B} and g E. We do not sacrifice anything by assuming that for every g, x(g) is either zero, or a vector of the -norm equal to 1. To ensure this, it is unnecessary to compute x(g). Indeed, it suffices to compute g, x(g). If this product is 0, we can reset x(g) = 0, Algorithm Let z 1,..., z t,... be the sequence of iterates of the proposed algorithm. At each iteration of the proposed algorithm, we solve a simple two-dimensional sub-problem with bound constraints in order to find the next iterate. Solving the sub-problem only requires objective and gradient calls, the minimization oracle (3.4), and a a priori bound D + on x. The bound D + only plays an instrumental role in the algorithm, and can be set to a quite loose value. Indeed, as the theoretical guarantee shows, the rate of convergence is independent of D +. but depends in fact on the true bound D induced by the problem, unknown and not required by the algorithm. The (t + 1)-th iterate z t+1 of the algorithm is given as the solution of the sub-problem { z t+1 Argmin F (z), z Conv{0, zt, D + z t } }, (3.5) z where z t := [ x(f (x(z t )), 1] is given by call to the minimization oracle as z t := [ x(f (x(z t ))), 1]. The algorithm proceeds by solving a sequence of such sub-problems. Description of the sub-problem We now gives more details on the subproblem, and explain the geometric intuition behind. Define K + [ρ] as K + [ρ] = { [x; ρ] K +, x ρ }, and consider the linear form [(ξ, ρ) f (x), ξ + λρ] for any ρ. For any ρ, the minimum of this linear form is reached at [ρ x(f (x)); ρ]. Therefore, as ρ varies, the set of minima of the linear form span a ray. This is where the loose a priori bound D + comes in. Consider a segment from this ray, namely, the segment corresponding to the minima when 0 ρ D + S(z) = {ρ[ x(f (x)); 1], 0 ρ D + }. For any z, the segment S(z) can be identified by a single call to the first-order oracle (objective and gradient evaluation), and a single call to the the minimization oracle (3.4) with g = f (x) for (K, ). Minimizing F ( ) on the convex hull of S(z) and z corresponds to minimizing F ( ) on the convex hull of the origin and the points z and D + z t, with z t := [ x(f (x(z t )), 1]. Getting back to (3.5), z t+1 = (x t+1, r t+1 ) is given by z t+1 = α t+1 z t + β t+1 z t (3.6) (α t+1, β t+1 ) = argmin {F (α z t + βz t ), α + β 1, α 0, β 0.} (3.7) α,β To solve the two-dimensional sub-problem one can utilize, for instance, the ellipsoid method, or any optimization algorithms using only first order information. Proposition 3.1. Let {z t } be a sequence generated by the algorithm (3.5) with z 1 = 0. Let D < be such that f(x) + λr f(0) and x r imply that r D. The algorithm based on recursion 3.5 is a descent algorithm. In addition, we have for all t = 2, 3,... F (z t ) F 8L f D 2 (t + 1) 1. 1 A close inspection of the proofs of the results below reveals that the discussed algorithms are robust with respect to errors in observation of f(x). In other words, a bound ν on the error in f(x) results in an extra term O(1)ν in the corresponding accuracy bounds. However, to streamline the presentation we do not discuss this modification here. 3

4 Algo. Time Training error Test error MovieLens10M Prox-Grad 42.37s ours 19.15s ImageNet Prox-Grad hrs ours 47.94hrs Table 1: Performance is measured in RMSE on the MovieLens10M dataset and misclassification error on the ILSVRC2010 ImageNet dataset. Note that the time is measured in secs on the Movie- Lens10M dataset, and hrs on the ILSVRC2010 ImageNet dataset. The result holds when a loose instrumental upper-bound D + is available. Yet, the algorithm does not require the knowledge of the upper-bound D (which always exist but is unknown to the algorithm), on which the convergence rate relies (see [10] for details). Acceleration In place of sub-problem 3.5, one can also leverage information gathered by previous iterations, and optimize instead on a convex hull based on previous iterates, an acceleration similar to the so-called restricted simplicial decomposition in the conditional gradient literature [4]. Let M N +, then sub-problem 3.5 can be replaced by z t+1 Argmin {F (z), z C t }. z where C t = { Conv{0; D+ z 0,..., D + z t }, for t M, Conv{0; z t M+1,..., z t ; D + z t M+1,..., D + z t }, for t > M. (3.8) Then, results of Proposition 3.1 still hold for {z t } defined in (3.8). 4 Experiments We conducted experiments on two examples of penalized learning formulations, resp. matrix completion with Gaussian noise and trace-norm regularization penalty, and multi-class classification with logistic loss and trace-norm regularization penalty [1, 2, 9]. We worked on the two corresponding datasets: i) MovieLens10M, ii) ImageNet dataset. We compared the proposed algorithm to the accelerated proximal gradient algorithm, denoted by Prox-Grad (cf. Table 1). MovieLens10M We utilise the proposed algorithm on the MovieLens10M dataset, corresponding to 10 7 ratings of users on movies. Same as in [12], we use half of the sample for training. Note that, because of the inherent sparsity of the problem, the matrix-vector computations can be handled very efficiently. Yet, experiments on this dataset are interesting, as they show that our approach is competitive with the state-of-the-art proximal gradient algorithm. Imagenet We test the algorithm on an image categorization application. We consider the Pascal ILSVRC2010 ImageNet dataset and focus on the Vertebrate-craniate subset, yielding 2943 classes with and average of 1000 examples each. We compute 65, 000-dimensional visual descriptors for each example using Fisher vector representation [9], a state-of-the-art feature vector representation in image categorization. Note that this representation yields dense feature vectors. In order to save enough RAM space to perform matrix-vector computations at each iteration, we set the size of the mini-batches to b = Note that the raw batch proximal gradient algorithm is inappropriate for such a large dataset. The straightforward stochastic gradient version of the proximal algorithm is out of scope, as it would involve an SVD per example. Thus we use as a contender the mini-batch version of the proximal gradient algorithm [5], and we use the same reasoning to set the mini-batch size of the proximal gradient algorithm. Results i show that the proposed algorithm has an edge over the mini-batch proximal gradient algorithm and manages to achieve a similar value of the objective significantly faster. 4

5 References [1] Y. Amit, M. Fink, N. Srebro, and S. Ullman. Uncovering shared structures in multiclass classification. In ICML, [2] A. Argyriou, T. Evgeniou, and M. Pontil. Convex multi-task feature learning. Machine Learning, 73(3), [3] F. R. Bach, R. Jenatton, J. Mairal, and G. Obozinski. Optimization with sparsity-inducing penalties. Foundations and Trends in Machine Learning, [4] D. Bertsekas. Nonlinear Programming. Athena Sci., [5] A. Cotter, O. Shamir, N. Srebro, and K. Sridharan. Better mini-batch algorithms via accelerated gradient methods. In NIPS, [6] V. Demyanov and A. Rubinov. Approximate Methods in Optimization Problems. American Elsevier, [7] M. Dudik, Z. Harchaoui, and J. Malick. Lifted coordinate descent for learning with trace-norm regularization. In AISTATS, [8] M. Frank and P. Wolfe. An algorithm for quadratic programming. Naval Research Logistics Quarterly, 3:95 110, [9] Z. Harchaoui, M. Douze, M. Paulin, M. Dudik, and J. Malick. Large-scale image classification with trace-norm regularization. In CVPR, [10] Z. Harchaoui, A. Juditsky, and A. Nemirovski. Conditional gradient algorithms for machine learning. Technical report, hal, [11] M. Jaggi. Revisiting Frank-Wolfe: Projection-free sparse convex optimization. In ICML, [12] M. Jaggi and M. Sulovský. A simple algorithm for nuclear norm regularized problems. In ICML, [13] S. Ji and J. Ye. An accelerated gradient method for trace norm minimization. In ICML, [14] G. Lan. An optimal method for stochastic composite optimization. Math. Program., [15] Y. Nesterov. Introductory lectures on convex optimization. A basic course. Kluwer, [16] Y. Nesterov. Gradient methods for minimizing composite objective function. Technical Report 76, CORE Discussion Paper, [17] T. K. Pong, S. J. Paul Tseng, and J. Ye. Trace norm regularization: Reformulations, algorithms, and multi-task learning. SIAM J. Optimization, 20(6): , [18] S. Shalev-Shwartz, A. Gonen, and O. Shamir. Large-scale convex minimization with a lowrank constraint. In ICML, [19] C. Shen, J. Kim, L. Wang, and A. van den Hengel. Positive semidefinite metric learning using boosting-like algorithms. JMLR, [20] S. Sra, S. Nowozin, and S. J. Wright. Optimization for Machine Learning. MIT Press,