Deformable Free Space Tilings for Kinetic Collision Detection
|
|
|
- Audrey Dorsey
- 5 years ago
- Views:
Transcription
1 Deformable Free Sace Tilings for Kinetic Collision Detection Pankaj K. Agarwal Julien Basch Leonidas J. Guibas John Hershberger Li Zhang Abstract We resent kinetic data structures for detecting collisions between a set of olygons that are not only moving continuously but whose shaes can also vary continuously with time. Unlike classical collision detection methods that rely on bounding volume hierarchies, our method is based on deformable tilings of the free sace surrounding the olygons. The basic shae of our tiles is that of a seudo-triangle, a shae sufficiently flexible to allow extensive deformation, yet structured enough to make detection of self-collisions easy. We show different schemes for maintaining seudo-triangulations as a kinetic data structure, and we analyze their erformance. Secifically, we first describe an algorithm for maintaining a seudo-triangulation of a oint set, and show that the seudo-triangulation changes only uadratically many times if oints move along algebraic arcs of constant degree. We then describe an algorithm for maintaining a seudotriangulation of a set of convex olygons. Finally, we extend our algorithm to the general case of maintaining a seudo-triangulation of a set of moving or deforming simle olygons. 1 Introduction Collision detection between moving objects is a fundamental roblem in comutational simulations of the hysical world. Because of its universality, it has been studied by several different communities, including robotics, comuter grahics, comuter-aided design, and comutational geometry. Several methods have been develoed for the case of rigid bodies moving freely in two and three dimensions. Though a hysical simulation involves several other comutational tasks, such as motion dynamics integration, grahics rendering, and collision resonse, collision detection remains one of the bottlenecks in such a system. A commonly used aroach to exedite the collision detection between comlex shaes is based on hierarchies of simle bounding volumes surrounding each of the objects. For a given lacement of two non-intersecting objects, their resective hierarchies are refined only to the coarsest level at which the rimitive shaes in the two hierarchies can be shown to be airwise disjoint. Motion in the hysical world is in general continuous over time, and many systems attemt to seed u collision checking by exloiting this temoral coherence, instead of reeating a full collision check ab initio at each time ste [11]. Swet volumes in sace or sace-time have been used towards this goal [4, 9]. Though fixed time-samling is customary for motion integration, collisions tend to be rather irregularly saced over time. If we know recisely the motion laws of the objects, then it makes sense to try to redict exactly when collisions will haen, instead of hoing to locate them with time samling. There have been a few theoretical aers in comutational geometry Center for Geometric Comuting, Deartment of Comuter Science, Box 90129, Duke University, Durham, NC 27708, USA. Comuter Science Deartment, Stanford University, Stanford, CA 94305, USA. Mentor Grahics Cor., 8005 SW Boeckman Road, Wilsonville, OR 97070, USA. 1
2 along these lines [5, 8, 12], but their results are not so useful in ractice because they use comlex data structures and are only alicable for limited tyes of motion. Recently Basch et al. [2] and Erickson et al. [6] resented algorithms for detecting collision between two olygons using the kinetic data structures framework, which was originally introduced by Basch et al. [3, 7]. Their algorithms avoid many of the roblems that arise in the fixed timesamling method. A kinetic data structure, or KDS for short, is built on the idea of maintaining a discrete attribute of objects in motion by animating a roof of its correctness through time. The roof consists of a set of elementary conditions, called certificates, based on the kinds of tests erformed by ordinary geometric algorithms (CCW tests in our case). Those certificates that can fail as a result of the motion of the olygons are laced in an event ueue, ordered according to their earliest failure time. When a certificate fails, the roof needs to be udated. Unless a collision has occurred, we erform this udate and continue the simulation. In contrast to fixed time ste methods, for which the fastest moving object gates the time ste for the entire system, a kinetic method is based on events (the certificate failures) that have a natural significance in terms of the roblem being addressed (collision detection in this case). Unlike the revious hierarchy-based algorithms, the algorithm by Basch et al. [2] maintains a decomosition of the common exterior of the two moving olygons. The cells of this decomosition deform continuously as the objects move. As long as all the cells in the decomosition remain disjoint, the decomosition itself acts as a KDS roof of non-collision between the objects. At certain times, cells become invalid because they self-intersect and the decomosition has to be modified. Unfortunately, in their aroach an extension to collision detection between many olygons is very exensive we have to construct such a decomosition for every air of olygons. In this aer we resent an algorithm for detecting collision between members of arbitrary sets of simle olygons as they move and/or deform in the lane. As in [2], we maintain a decomosition of the common exterior of olygons, the free sace, into deformable tiles. Ideally, we would like to maintain a decomosition so that the self-intersection of a cell of the decomosition is easy to detect, the decomosition is simle to udate when a self-intersection occurs, and the decomosition conforms to the motion of olygons so that self-intersections do not haen too many times. An obvious choice for the decomosition is a triangulation of the free sace. Although a triangulation satisfies the first two criteria, it contain too many cells and therefore has to be udated freuently. We will therefore use a seudo-triangulation as the decomosition, which has considerably fewer cells comared to a triangulation. Pseudo-triangles can flex as the objects move, and therefore the combinatorial structure of the tilings needs fewer udates. At the same time, the cells in a seudotriangulation have sufficiently simle shaes so that their self-intersections are easy to detect and the triangulation is easy to udate. Pseudo-triangulations have been used in the ast, but rimarily for various visibility roblems [10]. An additional benefit of our structure is that it can gracefully adat to object shaes that are themselves flexible. As our olygons move they can also deform and change shae. This additional flexibility imacts our data structure rimarily on the number of events it has to rocess but its basic nature and certification remains unchanged. In Section 2, we describe our model for motion, define seudo-triangulations, and describe the certificates needed to maintain a seudo-triangulation. In Section 3, we first describe how to maintain a seudo-triangulation for a set P of n moving oints in the lane, and show that it can be maintained in an outut-sensitive manner. For low-degree algebraic motion, the seudotriangulation changes about n 2 times. We can further refine the seudo-triangulation to maintain a triangulation of P, which changes O(n 7/3 ) times if each oint in P is moving with fixed velocity. To our knowledge, this is the first triangulation (without Steiner oints) that changes a sub-cubic number of times. In Section 4, we describe a scheme for maintaining the seudo-triangulation of a set P of k 2
3 disjoint olygons with a total of n vertices. We show that the greedy vertical seudo-triangulation roosed by Pocchiola and Vegter [10] can be maintained efficiently. A nice feature of this (or any minimal) seudo-triangulation is that the number of cells is only O(k), which is tyically much smaller than n, the total comlexity of the olygons. On the other hand, the size of any triangulation has to be at least Ω(n). We will show that we need a kinetic data structure of size O(k) to maintain this seudo-triangulation. But unlike the set of oints case, we do not have shar bounds on the number of events. Finally, in Section 5, we combine our algorithm for the convex case with the one in [2] to construct a seudo-triangulation for a set of airwise-disjoint simle olygons moving in the lane. It can easily be udated when a certificate fails. The number of certificates needed to maintain the correctness of the seudo-triangulation is roortional to the size of a minimum link subdivision searating the olygons [13], and is thus otimal in some sense. Our searation roof automatically adats to the comlexity of the relative lacement of the olygons, and its size will vary between O(k) (when the olygons are far from each other) and O(n) (when they are closely intertwined). A comact searation roof is imortant when objects are allowed to change their motion lan unredictably. Traditionally collision detection has been divided into two hases: the broad hase, in which one uses a simle-minded algorithm (tyically a bounding box check) to determine which airs of objects might collide and thus need further testing, and the narrow hase, in which these candidate airs get a more detailed collision test using a sohisticated algorithm. Note that our aroach based on deformable free sace tilings comletely obviates this distinction. The tiling effectively hides features of objects that are far away and treats the objects as euivalent to their convex hulls. As the objects get closer and more intertwined, their features get rogressively revealed and articiate in collision checks. Furthermore our framework can be extended in a straightforward way to deformable objects, a setting that no revious collision detection method had successfully addressed. Though this aer describes how to imlement the deformable tiling idea only in 2D, we are hoeful that 3D extensions will also be ossible. 2 Pseudo-Triangulations and their Certification In this section we define seudo-triangulations and discuss how we maintain them as objects move or deform continuously. Due to lack of sace, we do not elaborate on the kinds of motions and deformations allowed. The two key roerties that we need for our methods to work are that for each certificate or condition in the kinetic roof, we must be able to redict when it will fail next; we assume that our knowledge of the olygon motions allows us to comute the time of such an event at O(1) cost. for our analyses we need the roerty that the olygon motions are such that any articular certificate can fail at most a constant number of times; motions satisfying this constraint are called seudo-algebraic. 2.1 Pseudo-triangles A seudo-triangle in the lane is a simle olygon whose boundary consists of three concave chains, called side chains, that join at their endoints. The three endoints of a seudo-triangle are called corners. The edges incident uon the corners are called corner edges (Figure 1 (i)). For a vertex on the boundary of a seudo triangle, we denote L, R be the redecessor and the successor of 3
4 (i) (ii) Figure 1. (i) The examles of some seudo-triangles and non-seudo-triangles. The corner vertices are shown in the seudo-triangles. (ii) An examle of seudo triangulation of a olygon with holes. The dotted edges are the diagonal edges. along in the counterclockwise direction. Let S be a olygon with holes; some of the holes may be degenerate, i.e., they can be oints or segments. A seudo-triangulation T (S) of S is a lanar subdivision of the closure of S, so that each face of T (S) is a seudo-triangle and so that the interior of each face lies in the interior of S; see Figure 1 (ii) for an examle. In other words, T (S) is a collection of seudo-triangles with airwise-disjoint interiors, each lying inside S, that cover S. The vertices of T (S) are the same as the vertices of S, and each edge of T (S) is either an edge of S or a segment whose interior lies inside S; edges of the latter tye are called diagonals. We are interested in maintaining the seudo-triangulation of F(P), which, for brevity, we denote by T (P). Since a olygon (even with degenerate holes) can always be triangulated and a triangulated lanar subdivision is obviously a seudo-triangulation, a seudo-triangulation of S always exists. A seudo-triangulation T is called minimal if the union of any two faces in T is not a seudo-triangle. If T is not minimal, then there exists a diagonal d in T so that T remains a seudo-triangulation after the removal of d from it. Although minimal seudo-triangulations are not uniue, we can rove the following result on the size of minimal seudo-triangulations of F(P). Lemma 2.1. Let P be a set of k simle airwise-disjoint olygons as defined above. Suose m of these olygons are not oints, and suose there are a total of r reflex vertices 1 in P. Then there are k + m + r 2 seudo-triangles in any minimal seudo-triangulation of F(P). 2.2 Maintaining a seudo-triangulation We are interested in maintaining T (P), as F(P) deforms continuously. Secifically, we want to maintain T (P) as a kinetic data structure. As mentioned in the introduction, this is accomlished by maintaining a roof of the correctness of T (P), which consists of a small set of elementary conditions called certificates. As long as the certificates remain valid, the current combinatorial structure of T (P) is valid. T (P) is udated only when some certificate fails. A certificate failure is called an event. All the events are laced in an event ueue according to their failure time. The structure is then maintained by rocessing those events one by one. The efficiency of such a data structure deends on the size of the roof, the number of events, and the number of certificates that need to be udated at each event. In our set-u, we certify that each face in T (P) is a seudo-triangle and that the faces cover F(P). It turns out that the latter claim does not have to be exlicitly checked, assuming it was 1 For olygonal lines, all the interior vertices are assumed to be reflex vertices while the end vertices are not. A single oint is always assumed non-reflex. 4
5 1 L R L (i) R (ii) (iii) Figure 2. The certificates and udates for seudo triangulation. (i) The reflex and corner certificates; (ii) the udate for a reflex certificate failure; (iii) the udate for a corner certificate failure. true at the beginning of time. Thus we need to certify only the following two conditions for each seudo-triangle in T (P): 1. Each side chain C is concave, i.e. for each interior vertex of C, the angle L R > π (or the signed area of L R is negative). We call these certificates reflex certificates. 2. The side chains of a seudo-triangle join only at their endoints, i.e. for each corner vertex of, the angle L R < π (or the signed area of L R is ositive). We call such certificates corner certificates. When the reflex certificate of fails, we connect the vertices adjacent to, say 1, 2, to maintain the seudo-triangularity of. To maintain the seudo-triangulation, we may also have to udate other seudo-triangles, deending on the edges adjacent to. If both edges adjacent to are boundary edges, then we add a triangle 1 2 to T (P). If only one edge, say 1, is a diagonal edge, then 1 must be on another seudo-triangle 1. In this case, we delete the edge 1 and merge the triangle 1 2 into the seudo-triangle 1. If both 1, 2 are diagonal edges, we then delete one of 1 or 2 : which edge is deleted deends on the secific seudo-triangulation we are maintaining; we will exlain the choice for each seudo-triangulation later in the aer. When the corner certificate of fails, we collase the corner. Suose that the vertices adjacent to are 1, 2 and when the concave certificate corresonding to fails, 2 lies on the edge 1. We then delete the edge 1 and add the edge 1 2 to maintain the seudo-triangularity of. This rocess also effectively adds the oint 2 to the side chain of the other seudo-triangle incident to the edge 1. Since there is only one way to udate the seudo-triangulation when a corner certificate fails, we will not describe udates for this case in the following sections. In addition, we also have to maintain the boundary F(P). F(P) \ P is automatically maintained by the algorithm. By regarding P as a concave chain with resect to the exterior of P, it can also be maintained using reflex certificates for each vertex on the hull. We omit the details. Since the seudo-triangulation is not a canonical structure (there may be many seudo triangulations of F(P)), it is not clear which seudo-triangulation we are maintaining. To avoid this ambiguity, we first describe a static algorithm that constructs a secific seudo-triangulation of F(P). We then assume that, at any time t, the kinetic data structure maintains the seudotriangulation that the static algorithm would have constructed on P(t). This way, the structure is canonical, and it is more convenient for the analysis. Such aroach has been taken in maintaining other structures, for examle, the binary sace artitioning structure in [1]. To maintain this invariant, we need additional certificates. When these certificates fail, we usually udate the structure by the fliing oeration: For any diagonal edge e, consider the two seudo-triangles 1, 2 that contain e. The union of 1, 2 forms a seudo-uadrangle a cell 5
6 u() u() d() (i) d() (ii) Figure 3. The incremental seudo-triangulation of a oint set. In (i), the swee line has just assed ; (ii) shows the final seudo-triangulation. whose boundary consists of four concave chains. Besides e, there is exactly one other diagonal edge inside, which is called the shadow edge of e. The uadrangle can be decomosed into two seudo-triangles in two ways, one by adding e and the other by adding e s shadow edge. The fliing oeration relaces e by e. 3 Pseudo-Triangulation for Points In this section, we assume P to be a set of n oints. we define the incremental seudo-triangulation for P, and show how to maintain it efficiently. We also show it can be refined to maintain a triangulation of P. 3.1 Incremental seudo-triangulation The seudo-triangulation for oints is built in an incremental manner as follows. We first sort the oints in increasing order of their x-coordinates. Suose that 1, 2,..., n is the sorted seuence. We then lace a vertical line at 1 and swee it from left to right to build the seudo-triangulation incrementally. When the swee line asses the oint k, we draw two tangent segments from k to the convex hull of P k 1. Denote by u( k ) and d( k ) the left endoints of the uer and lower tangent segments to P k 1 from k, resectively (Figure 3). The concave chain on P k 1 between u( k ) and d( k ) and line segments k u( k ), k d( k ) form a seudo-triangle ( k ) its boundary consists of a concave chain and two single edges. Let C( k ) denote the concave chain on ( k ). The three corners of ( k ) are the oints k, d( k ), and u( k ). After rocessing every oint in P, we obtain a seudo-triangulation, which is called the incremental seudo-triangulation (IPT) of P. 3.2 Maintaining the incremental seudo-triangulation As the oints move, IPT(P) at discrete times. changes continuously, but its combinatorial structure changes only Lemma 3.1. As long the x-ordering of the oints in P does not change, the reflex and corner certificates certify the incremental seudo-triangulations. In view of this lemma, as long as the x-ordering does not change, we have to udate IPT (P) only when a reflex or corner certificate fails. When a corner event fails, the structure can be udated as described in Section 2.2. When a reflex certificate fails, we have two choices as which edge to delete such choice is not difficult, and we omit the details in this abstract. 6
7 u() u() r r u() r u() r r r r r d() d() d() d() Figure 4. (i) Two oints exchange in x-order. (ii) Fan triangulation of IPT (P). Next, we consider the case in which two oints exchange in x-order. Although such an event does not affect the validity of the seudo-triangulation, it does cause a change to IPT (P) since the incremental ordering of the oints changes. Suose that asses from the left at time t and is above (Figure 4). Let r be d() just before time t, and let r be u() immediately after time t. Then the structure is udated by switching the edge r with the edge r a fliing oeration defined in Section 2.2. The oint r can be found by comuting a tangent segment from to the concave chain between u() and d(), which can be done in O(log n) time. Notice that in this descrition, each event changes IPT (P). Thus, the method is outut-sensitive. We have shown that Theorem 3.2. The incremental seudo-triangulation can be maintained in an outut-sensitive manner. Each udate of the structure takes O(log n) time. In the following, we shall bound the number of changes to IPT (P) for oints in constant degree algebraic motion. 3.3 Combinatorial changes to IPT(P) We now obtain an uer bound on the number of combinatorial changes to IPT (P), i.e., the number of events, under the assumtion that the degree of motion of P is fixed. We define a function φ (t) for two distinct oints, P: if at time t, is to the left of, then φ (t) is the sloe of the line that asses through and ; otherwise, φ (t) is undefined. Since the motion has constant degree, the x-order of a air of oints can switch only a constant number of times. Thus, each φ (t) consists of a constant number of arcs, all of which are ortions of a fixed-degree olynomial. Consider the family of functions Φ = {φ P}. By our assumtions any two arcs in Φ intersect a constant number of times, say, s 2. For a oint to be d() at time t, φ (t) must have the largest value among all the oints in P. This is to say, the number of changes to d() is the same as the combinatorial comlexity of the uer enveloe of Φ, which is bounded by λ s (n) (λ s (n) is the maximum length of an (n, s) Davenort-Schinzel seuence and is roughly linear.). Similarly, we can bound the number of changes to u() by λ s (n). Summing over all the vertices in P, we thus have Theorem 3.3. When the oints of P move algebraically with constant degree, IPT(P) changes O(nλ s (n)) times, where s is a constant that deends on the degree of the motion. 3.4 Triangulation of P It is very easy to obtain a triangulation of P from IPT (P) by connecting each oint to every interior oint on C(), thereby creating a fan inside each (). We call such a triangulation a fan triangulation. Although IPT (P) changes only nearly uadratically many times, we are not able 7
8 s 2 s 1 s 3 (i) (ii) (iii) Figure 5. (i) Intersecting and non-intersecting tangents: s 1, s 2 are intersecting, but s 1, s 3 and s 2, s 3 are nonintersecting tangents. (ii) Greedy vertical seudo-triangulation. (iii) Left-to-right roerty. The solid segment is an edge in GVPT. The dotted ones are the free tangents it crosses. to rove a similar bound on the number of changes in the fan triangulation. The roblem comes from the x-ordering event, which we rocess by switching a fan of to a fan of, or vice versa (Figure 4 (ii)). Using the revious notation, the cost of such switching is roortional to the length of the chain between r and r. In the worst case, it might be Θ(n). This would give us a naïve bound of O(n 3 ) on the number of changes to the fan triangulation. For linear motion, we obtain a better uer bound on the number of changes to the fan triangulation by a global argument. We omit the roof from this abstract. Theorem 3.4. For oints in linear motion, the number of changes to the fan triangulation is bounded by O(n 4/3 λ s (n)), where s is a constant. The obvious oen roblems are whether it is ossible to extend this result to algebraic motions and whether the bound is tight. 4 Pseudo-Triangulation for Convex Polygons Next we consider the case in which P is a set of k convex olygons with a total of n vertices. We describe a different seudo-triangulation for P, called the greedy vertical seudo-triangulation, which is based on a result by Pocchiola and Vegter [10]. They introduced greedy seudo-triangulation as a tool to comute the visibility comlex of a set of convex olygons. We will modify their algorithm for our alication 4.1 Greedy seudo-triangulation for convex olygons There are exactly four bi-tangent segments between any two disjoint convex olygons. A bi-tangent is called free if it does not intersect the interior of any object in P. Let s and s be two free bitangents with a common endoint v, which is a vertex of a olygon P P. We say that s and s cross at v if P lies in the wedge of angle greater than π formed by s and s ; see Figure 5. 2 We say that two free bi-tangents intersect either if they share an interior oint or if they have a common endoint and they cross at that endoint. For any linear ordering on the free tangents, we can build a corresonding greedy triangulation T (P) as follows. We first sort the tangents by ordering. We then scan through this list and maintain a set S of tangents that we have added to the seudo-triangulation so far. At each ste, we ick the next tangent segment s in the sorted seuence and check whether it intersects any tangents in S. If s does not intersect any segment of 2 Intuitively, if we smooth the olygon P by taking the Minkowski sum of P with a disk of a sufficiently small radius, say δ, and we translate s and s by at most δ so that they become tangents to the resulting olygons at their endoints, then s and s cross at v if and only if the translated coies of s and s intersect. 8
9 S, we add it to S; otherwise, we discard s. After rocessing all the segments, we obtain a set of non-intersecting free tangents. It is shown in [10] that S = 3k 3, and that together with the object boundaries, S forms a seudo-triangulation of F(P) consisting of 2k 2 seudo-triangles. By Lemma 2.1, this rocedure constructs a minimal seudo-triangulation. For any line segment s, define θ(s) to be the minimum ositive angle by which we have to rotate a vertical segment in the clockwise direction so that it becomes arallel to s. We order all the free tangents in increasing order of θ( ). The greedy seudo-triangulation created using this ordering is called the greedy vertical seudo-triangulation (GVPT ) and is denoted by G(P) (Figure 5 (ii)). It is shown in [10] that G(P) can be constructed in O(k log n) time, rovided that each olygon is reresented as an array storing its vertices in a clockwise (or counterclockwise) order. The following local rule determines whether a free bi-tangent is in G(P). Lemma 4.1 (Left-to-right roerty). A bi-tangent segment s is in G(P) if and only if θ(s) < θ(s ) for each free bi-tangent s intersected by s (Figure 5 (iii)). Recall that if we relace an edge in a seudo-triangulation with its shadow edge, we still obtain a seudo-triangulation. It turns out that in G(P) the shadow edge of an edge s is minimal in the ordering among all free bi-tangents crossing s. This imlies the following roerty: Lemma 4.2 (Local roerty). Suose that s is an edge in T (P). Denote by the same ordering as excet assigning s as the maximum element of. Then T (P) can be obtained from T (P) by relacing s with its shadow edge. By this lemma, if the ordering of an edge changes, we just erform a local fli oeration to fix the greedy seudo-triangulation. 4.2 Maintaining the greedy seudo-triangulation We now describe how to maintain G(P) as a KDS so that it can be udated efficiently as the olygons in P move or deform. As described in Section 2.2, we maintain corner and reflex certificates for each seudo-triangle in G(P). In addition, for each diagonal edge s of G(P), we maintain a diagonal certificate to certify that θ(s) < θ(s ), where s is the shadow edge of s in G(P). This adds the reuirement to maintain the shadow edges although such edges do not aear in G(P). Again, the shadow edges can be maintained in the same manner by corner and reflex certificates. We will show that these certificates are sufficient to maintain G(P). As in Section 3, we can rove the following analogue to Lemma 3.1. The roof is omitted from this version. Lemma 4.3. If no diagonal certificate fails, then G(P) changes only when one of the corner or reflex certificates fails. When a corner or reflex certificate fails, we can udate G(P) as described in Section 2.2, excet for one subtle issue in the case of reflex certificates. When an interior vertex of a side chain... L R... ceases to be a reflex vertex, we add the edge L R and we have to delete one of the edges L and R. Instead of deleting one of them arbitrarily, we delete L if θ( L ) > θ( R ); see Figure 6. Next, we consider diagonal certificates. If the certificate of a diagonal edge s fails, then either s or its shadow edge is vertical. When such an event haens, the sloe ordering of an edge jums from the minimum to maximum, or vice versa. By the local roerty of greedy seudo-triangulations, we can simly erform a fliing oeration to s to maintain G(P). 9
10 P P 3 2 P 3 P 1 P 1 L R R P 2 L Figure 6. The reflex(from left to right) and corner(from right to left) events and the udates. When a reflex certificate fails, we choose the edge with smaller sloe, as shown in the right figure. Since G(P) has O(k) diagonals and seudo-triangles, the number of corner and diagonal certificates is O(k). We assume that the olygons remain convex at all times, therefore it suffices to maintain reflex certificates for a vertex only if it is adjacent to a diagonal edge, i.e., a free bi-tangent. The number of such vertices is also O(k). Hence, we obtain the following: Theorem 4.4. G(P) can be maintained by using a structure with O(k) certificates. Each event can be rocessed in time O(log n). This data structure works even if the olygons deform continuously over time, as long as they remain convex at all times. What matters is the number of events. The rigid motion can give us better bounds as stated in Theorem Combinatorial changes to G(P) Next, we bound the number of changes to G(P) if the degree of motion of P is fixed. It can be shown that a corner or reflex certificate fails when three olygons of P become collinear, i.e., a line is tangent to three olygons. Hence, a combinatorial change in G(P) haens only when three olygons of P are collinear or when a bi-tangent becomes vertical. The number of such events can be bounded by the following lemma. Lemma 4.5. Suose that P 1, P 2, P 3 are convex olygons with n 1, n 2, n 3 vertices, resectively, and the degree of their motion is constant. They can become collinear O(n 1 + n 2 + n 3 ) and O(n 1 n 2 + n 1 n 3 + n 2 n 3 ) times for translational and rigid motions, resectively. The bi-tangent between P 1, P 2 can become vertical O(1) and O(n 1 + n 2 ) times for translational and rigid motions, resectively. Alying this lemma to all trilets of P, we obtain the following weak uer bounds on the number of changes to G(P). Theorem 4.6. Let P be a set of k olygons with a total of n vertices. G(P) changes O(kn 2 ) times if the degree of motion of P is fixed. If the motion is translational, the number of changes is only O(k 2 n). If the olygons may deform, the number of changes is bounded by O(n 3 ). 5 Pseudo-Triangulation for Simle Polygons In this section, we consider the case in which P is a set of k airwise-disjoint simle olygons with a total of n vertices. We will describe a method for maintaining a seudo-triangulation of P by combining our algorithm for convex olygons with the algorithm by Basch et al. [2] for two simle olygons. 10
11 (i) (ii) Figure 7. The mixed seudo-triangulation. (i) F 1(P) and F 2(P) are shaded differently. (ii) Mixed seudotriangulation; thick edges denote the boundary between F 1(P) and F 2(P). 5.1 The mixed seudo-triangulation For each P P, define the relative geodesic cycle C(P ) of P to be the shortest cycle in F(P) with the same homotoy tye as P. The region enclosed by C(P ) is called the relative convex hull and is denoted by P. We decomose F(P) into two arts F 1 (P) = F(P) ( P ) and F 2 (P) = F(P)\ P. We comute seudo-triangulations T (F 1 (P)) and T (F 2 (P)) searately. These two triangulations together give the mixed seudo-triangulation of P. First, we consider F 1 (P). Since the interiors of all the relative convex hulls are airwise disjoint, we can comute a seudo-triangulation of each of them searately. We triangulate each P as in [2]. Following [2], we define the inned relative geodesic cycle of P, with resect to a inning oint set B (a subset of the vertices of P ), to be the shortest cycle in F(P) that asses through the vertices in B and has the same homotoy tye as P. The inned relative convex hull of P with resect to B is the region enclosed by the inned relative geodesic cycle. If B contains all the vertices of P, the inned relative convex hull of P is P itself. Consider a balanced binary tree T (P ) with the vertices of P as leaves, in the order they aear on P ; each internal node stores the vertex from its left child. We can then build log P inned relative geodesic cycles, where the inning set of each cycle is the set of vertices on the same level of T (P ). By overlaying these layers, we can obtain a seudo-triangulation of P \ P. This seudo-triangulation is called the external relative geodesic triangulation. Refer to [2] for the maintenance and bounds on the number of changes of this structure. Now, we consider F 2 (P). In the following, we generalize the greedy seudo-triangulation, defined in Section 4, to a connected olygonal subdivision. Consider a connected olygonal region F. A vertex v of F is called a corner vertex if the interior angle at v is less than 180 ; otherwise, v is called a reflex vertex. For a oint on F, a line segment in F is called tangent to F at if is a corner vertex or the line assing through, locally suorts F at. (The intuition behind the definition of tangent for corner vertices comes from the case in which a corner is formed by two searate convex objects whose boundaries touch. Then a tangent segment to the corner is indeed tangent to one of the two convex objects.) For two vertices, on F, the line segment is called a free bi-tangent if lies in F and is tangent to F at both and. We now construct the greedy vertical seudo-triangulation of F, as described in Section 4. It can be shown that the algorithm constructs a minimal seudo-triangulation of F. The following lemma bounds the number of seudo-triangles in such a seudo-triangulation. Lemma 5.1. If F consists of k connected comonents and m corner vertices, the number of seudo-triangles in the greedy seudo triangulation of F is O(k + m). The relative geodesic triangulation T (F 1 (P) and greedy seudo-triangulation T (F 2 (P)) together form a seudo-triangulation of F(P), which we call the mixed seudo-triangulation (Fig- 11
12 ure 7). Next, we bound the size of the mixed seudo-triangulation. We call a diagonal edge of the mixed seudo-triangulation a bridge edge if it connects two different olygons of P. As we will see later, bridge edges lay an imortant role in maintenance of the seudo-triangulation. Lemma 5.2. F 2 (P) consists of O(k) connected comonents and O(k) bridge edges and corner vertices. Lemmas 5.1 and 5.2 imly the following. Corollary 5.3. The greedy triangulation T (F 2 (P)) of F 2 (P) has O(k) seudo-triangles. Next, we bound the size of T (F 1 (P)). We will focus on the bridge edges in F 1 (P). Basch et al. [2] have shown that any line segment lying inside F(P) crosses O(log n) bridge edges, and thus the number of bridge edges is O(τ log n), where τ is the size of the min-link searator between two simle olygons. Here, we generalize their result to our setu by arguing that any free line segment can cross at most two relative convex hulls. Lemma 5.4. Any free line segment crosses O(log n) bridge edges of T (F 1 (P)). A minimum link subdivision is a olygonal subdivision of the lane, using as few (line segment) edges as ossible, such that each P P is contained in its own face of the subdivision. A minimum link searator for a olygon P P is a simle olygon homotoic to P with as few edges as ossible. Consider any Jordan cycle C in F(P) that is homotoic to P. Clearly, C must intersect all the bridge edges incident to P because C searates P from other objects in P. Suose that C consists of τ line segments. Since each line segment on C crosses at most O(log n) bridge edges connected to P and each bridge edge is crossed at least once, we can conclude that the number of bridge edges incident to P is bounded by O(τ log n). Therefore, we have the following result on the number of bridge edges. Lemma 5.5. The number of bridge edges in T (F 1 (P)) is bounded by O(κ log n), where κ is the number of edges in a minimum link subdivision of P. For each olygon P in P, the number of bridge edges connected to P is bounded by O(τ(P ) log n), where τ(p ) is the number of edges in a minimum link searator of P. Thus, we obtain the following bounds on the size of the mixed seudo triangulation by combining Corollary 5.3 and Lemma 5.5. Theorem 5.6. The size of the mixed seudo-triangulation is O(n), and among all the diagonal edges, only O(κ log n) edges are bridge edges, where κ is the number of edges in a minimum link subdivision of P. 5.2 Maintaining the mixed seudo-triangulation As shown in [2], the external relative geodesic triangulation can be maintained by corner and reflex certificates only, and there are local rules to decide which edge to select when a reflex certificate fails. Therefore, the mixed triangulation can be easily maintained, although it comrises two comletely different structures. As argued before, the number of certificates in the certification structure of T (P) is roortional to the number of bridge edges in T (P). According to Lemmas 5.2 and 5.5, we may bound the certificates for certifying T (P) as follows. 12
13 Theorem 5.7. The number of certificates in T (P) is bounded by O(κ log n), where κ is the number of edges in the minimum link subdivision of P. For each olygon P in P, the number of certificates involving P is bounded by O(τ(P ) log n + k), where τ(p ) is the number of edges in the minimum link searator of P. A trivial bound on the number of changes to the mixed seudo-triangulation for olygons in rigid motion is O(n 3 ), which is the number of times when three vertices become collinear. 6 Conclusions We have shown how to efficiently maintain seudo-triangulations of the free sace for oints, convex, and simle olygons moving around in the lane. In addition to collision detection, the seudotriangulation structure rovides a simle way for walking around the free sace and erforming oerations such as ray shooting and other visibility ueries. Unlike any revious collision detection method, our deforming tilings can be adated to work for deformable objects, thus enabling new alications where simulation of flexible shaes is imortant. An extension of our ideas to 3D resents the next obvious challenge. References [1] P. K. Agarwal, L. J. Guibas, T. M. Murali, and J. S. Vitter. Cylindrical static and kinetic binary sace artitions. In Proc. 13th Annu. ACM Symos. Comut. Geom., ages 39 48, [2] J. Basch, J. Erickson, L. J. Guibas, J. Hershberger, and L. Zhang. Kinetic collision detection for two simle olygons. In Proc. 9th ACM-SIAM Symos. Discrete Algorithms, ages , [3] J. Basch, L. J. Guibas, and J. Hershberger. Data structures for mobile data. In Proc. 8th ACM-SIAM Symos. Discrete Algorithms, ages , [4] S. Cameron. Collision detection by four-dimensional intersection testing. In Proc. IEEE Internat. Conf. Robot. Autom., ages , [5] D. Estein and J. Erickson. Raising roofs, crashing cycles, and laying ool: Alications of a data structure for finding airwise interactions. In Proc. 14th Annu. ACM Symos. Comut. Geom., ages 58 67, [6] J. Erickson, L. J. Guibas, J. Stofi, and L. Zhang. Searation-sensitive kinetic collision detection for convex objects. In Proc. 9th ACM-SIAM Symos. Discrete Algorithms, [7] L. J. Guibas. Kinetic data structures: A state of the art reort. In Proc. 3rd Worksho on Algorithmic Foundations of Robotics, age to aear, [8] P. Guta, R. Janardan, and M. Smid. Fast algorithms for collision and roximity roblems involving moving geometric objects. Comut. Geom. Theory Al., 6: , [9] P. M. Hubbard. Collision detection for interactive grahics alications. IEEE Trans. Visualization and Comuter Grahics, 1(3): , Set [10] M. Pocchiola and G. Vegter. Toologically sweeing visibility comlexes via seudo-triangulations. Discrete Comut. Geom., 16: , Dec [11] M. K. Ponamgi, D. Manocha, and M. C. Lin. Incremental algorithms for collision detection between general solid models. In Proc. ACM Siggrah Symos. Solid Modeling, ages , [12] E. Schömer and C. Thiel. Efficient collision detection for moving olyhedra. In Proc. 11th Annu. ACM Symos. Comut. Geom., ages 51 60, [13] S. Suri. Minimum link aths in olygons and related roblems. Ph.D. thesis, Det. Comut. Sci., Johns Hokins Univ., Baltimore, MD,
Lecture 3: Geometric Algorithms(Convex sets, Divide & Conquer Algo.)
 Advanced Algorithms Fall 2015 Lecture 3: Geometric Algorithms(Convex sets, Divide & Conuer Algo.) Faculty: K.R. Chowdhary : Professor of CS Disclaimer: These notes have not been subjected to the usual
Advanced Algorithms Fall 2015 Lecture 3: Geometric Algorithms(Convex sets, Divide & Conuer Algo.) Faculty: K.R. Chowdhary : Professor of CS Disclaimer: These notes have not been subjected to the usual
CMSC 425: Lecture 16 Motion Planning: Basic Concepts
 : Lecture 16 Motion lanning: Basic Concets eading: Today s material comes from various sources, including AI Game rogramming Wisdom 2 by S. abin and lanning Algorithms by S. M. LaValle (Chats. 4 and 5).
: Lecture 16 Motion lanning: Basic Concets eading: Today s material comes from various sources, including AI Game rogramming Wisdom 2 by S. abin and lanning Algorithms by S. M. LaValle (Chats. 4 and 5).
Cross products. p 2 p. p p1 p2. p 1. Line segments The convex combination of two distinct points p1 ( x1, such that for some real number with 0 1,
 CHAPTER 33 Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
CHAPTER 33 Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
We will then introduce the DT, discuss some of its fundamental properties and show how to compute a DT directly from a given set of points.
 Voronoi Diagram and Delaunay Triangulation 1 Introduction The Voronoi Diagram (VD, for short) is a ubiquitious structure that aears in a variety of discilines - biology, geograhy, ecology, crystallograhy,
Voronoi Diagram and Delaunay Triangulation 1 Introduction The Voronoi Diagram (VD, for short) is a ubiquitious structure that aears in a variety of discilines - biology, geograhy, ecology, crystallograhy,
Cross products Line segments The convex combination of two distinct points p
 CHAPTER Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
CHAPTER Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
Convex Hulls. Helen Cameron. Helen Cameron Convex Hulls 1/101
 Convex Hulls Helen Cameron Helen Cameron Convex Hulls 1/101 What Is a Convex Hull? Starting Point: Points in 2D y x Helen Cameron Convex Hulls 3/101 Convex Hull: Informally Imagine that the x, y-lane is
Convex Hulls Helen Cameron Helen Cameron Convex Hulls 1/101 What Is a Convex Hull? Starting Point: Points in 2D y x Helen Cameron Convex Hulls 3/101 Convex Hull: Informally Imagine that the x, y-lane is
Lecture 2: Fixed-Radius Near Neighbors and Geometric Basics
 structure arises in many alications of geometry. The dual structure, called a Delaunay triangulation also has many interesting roerties. Figure 3: Voronoi diagram and Delaunay triangulation. Search: Geometric
structure arises in many alications of geometry. The dual structure, called a Delaunay triangulation also has many interesting roerties. Figure 3: Voronoi diagram and Delaunay triangulation. Search: Geometric
Lecture 8: Orthogonal Range Searching
 CPS234 Comutational Geometry Setember 22nd, 2005 Lecture 8: Orthogonal Range Searching Lecturer: Pankaj K. Agarwal Scribe: Mason F. Matthews 8.1 Range Searching The general roblem of range searching is
CPS234 Comutational Geometry Setember 22nd, 2005 Lecture 8: Orthogonal Range Searching Lecturer: Pankaj K. Agarwal Scribe: Mason F. Matthews 8.1 Range Searching The general roblem of range searching is
Computing the Convex Hull of. W. Hochstattler, S. Kromberg, C. Moll
 Reort No. 94.60 A new Linear Time Algorithm for Comuting the Convex Hull of a Simle Polygon in the Plane by W. Hochstattler, S. Kromberg, C. Moll 994 W. Hochstattler, S. Kromberg, C. Moll Universitat zu
Reort No. 94.60 A new Linear Time Algorithm for Comuting the Convex Hull of a Simle Polygon in the Plane by W. Hochstattler, S. Kromberg, C. Moll 994 W. Hochstattler, S. Kromberg, C. Moll Universitat zu
The Edge-flipping Distance of Triangulations
 The Edge-fliing Distance of Triangulations Sabine Hanke (Institut für Informatik, Universität Freiburg, Germany hanke@informatik.uni-freiburg.de) Thomas Ottmann (Institut für Informatik, Universität Freiburg,
The Edge-fliing Distance of Triangulations Sabine Hanke (Institut für Informatik, Universität Freiburg, Germany hanke@informatik.uni-freiburg.de) Thomas Ottmann (Institut für Informatik, Universität Freiburg,
COT5405: GEOMETRIC ALGORITHMS
 COT5405: GEOMETRIC ALGORITHMS Objects: Points in, Segments, Lines, Circles, Triangles Polygons, Polyhedra R n Alications Vision, Grahics, Visualizations, Databases, Data mining, Networks, GIS Scientific
COT5405: GEOMETRIC ALGORITHMS Objects: Points in, Segments, Lines, Circles, Triangles Polygons, Polyhedra R n Alications Vision, Grahics, Visualizations, Databases, Data mining, Networks, GIS Scientific
Randomized algorithms: Two examples and Yao s Minimax Principle
 Randomized algorithms: Two examles and Yao s Minimax Princile Maximum Satisfiability Consider the roblem Maximum Satisfiability (MAX-SAT). Bring your knowledge u-to-date on the Satisfiability roblem. Maximum
Randomized algorithms: Two examles and Yao s Minimax Princile Maximum Satisfiability Consider the roblem Maximum Satisfiability (MAX-SAT). Bring your knowledge u-to-date on the Satisfiability roblem. Maximum
arxiv: v1 [math.gt] 1 May 2018
![arxiv: v1 [math.gt] 1 May 2018 arxiv: v1 [math.gt] 1 May 2018](/thumbs/94/118297333.jpg) CIRCUIT PRESENTATION AND LATTICE STICK NUMBER WITH EXACTLY 4 z-sticks HYOUNGJUN KIM AND SUNGJONG NO arxiv:805.0023v [math.gt] May 208 Abstract. The lattice stick number s L(L) of a link L is defined to
CIRCUIT PRESENTATION AND LATTICE STICK NUMBER WITH EXACTLY 4 z-sticks HYOUNGJUN KIM AND SUNGJONG NO arxiv:805.0023v [math.gt] May 208 Abstract. The lattice stick number s L(L) of a link L is defined to
Constrained Empty-Rectangle Delaunay Graphs
 CCCG 2015, Kingston, Ontario, August 10 12, 2015 Constrained Emty-Rectangle Delaunay Grahs Prosenjit Bose Jean-Lou De Carufel André van Renssen Abstract Given an arbitrary convex shae C, a set P of oints
CCCG 2015, Kingston, Ontario, August 10 12, 2015 Constrained Emty-Rectangle Delaunay Grahs Prosenjit Bose Jean-Lou De Carufel André van Renssen Abstract Given an arbitrary convex shae C, a set P of oints
Directed File Transfer Scheduling
 Directed File Transfer Scheduling Weizhen Mao Deartment of Comuter Science The College of William and Mary Williamsburg, Virginia 387-8795 wm@cs.wm.edu Abstract The file transfer scheduling roblem was
Directed File Transfer Scheduling Weizhen Mao Deartment of Comuter Science The College of William and Mary Williamsburg, Virginia 387-8795 wm@cs.wm.edu Abstract The file transfer scheduling roblem was
An improved algorithm for Hausdorff Voronoi diagram for non-crossing sets
 An imroved algorithm for Hausdorff Voronoi diagram for non-crossing sets Frank Dehne, Anil Maheshwari and Ryan Taylor May 26, 2006 Abstract We resent an imroved algorithm for building a Hausdorff Voronoi
An imroved algorithm for Hausdorff Voronoi diagram for non-crossing sets Frank Dehne, Anil Maheshwari and Ryan Taylor May 26, 2006 Abstract We resent an imroved algorithm for building a Hausdorff Voronoi
Taut ideal triangulations of 3-manifolds
 Abstract Taut ideal triangulations of 3-manifolds Marc Lackenby Mathematical Institute, Oxford University, 24-29 St Giles, Oxford OX1 3LB, UK Email: lackenby@maths.ox.ac.uk A taut ideal triangulation of
Abstract Taut ideal triangulations of 3-manifolds Marc Lackenby Mathematical Institute, Oxford University, 24-29 St Giles, Oxford OX1 3LB, UK Email: lackenby@maths.ox.ac.uk A taut ideal triangulation of
Shuigeng Zhou. May 18, 2016 School of Computer Science Fudan University
 Query Processing Shuigeng Zhou May 18, 2016 School of Comuter Science Fudan University Overview Outline Measures of Query Cost Selection Oeration Sorting Join Oeration Other Oerations Evaluation of Exressions
Query Processing Shuigeng Zhou May 18, 2016 School of Comuter Science Fudan University Overview Outline Measures of Query Cost Selection Oeration Sorting Join Oeration Other Oerations Evaluation of Exressions
Truth Trees. Truth Tree Fundamentals
 Truth Trees 1 True Tree Fundamentals 2 Testing Grous of Statements for Consistency 3 Testing Arguments in Proositional Logic 4 Proving Invalidity in Predicate Logic Answers to Selected Exercises Truth
Truth Trees 1 True Tree Fundamentals 2 Testing Grous of Statements for Consistency 3 Testing Arguments in Proositional Logic 4 Proving Invalidity in Predicate Logic Answers to Selected Exercises Truth
Extracting Optimal Paths from Roadmaps for Motion Planning
 Extracting Otimal Paths from Roadmas for Motion Planning Jinsuck Kim Roger A. Pearce Nancy M. Amato Deartment of Comuter Science Texas A&M University College Station, TX 843 jinsuckk,ra231,amato @cs.tamu.edu
Extracting Otimal Paths from Roadmas for Motion Planning Jinsuck Kim Roger A. Pearce Nancy M. Amato Deartment of Comuter Science Texas A&M University College Station, TX 843 jinsuckk,ra231,amato @cs.tamu.edu
Grouping of Patches in Progressive Radiosity
 Grouing of Patches in Progressive Radiosity Arjan J.F. Kok * Abstract The radiosity method can be imroved by (adatively) grouing small neighboring atches into grous. Comutations normally done for searate
Grouing of Patches in Progressive Radiosity Arjan J.F. Kok * Abstract The radiosity method can be imroved by (adatively) grouing small neighboring atches into grous. Comutations normally done for searate
Sensitivity Analysis for an Optimal Routing Policy in an Ad Hoc Wireless Network
 1 Sensitivity Analysis for an Otimal Routing Policy in an Ad Hoc Wireless Network Tara Javidi and Demosthenis Teneketzis Deartment of Electrical Engineering and Comuter Science University of Michigan Ann
1 Sensitivity Analysis for an Otimal Routing Policy in an Ad Hoc Wireless Network Tara Javidi and Demosthenis Teneketzis Deartment of Electrical Engineering and Comuter Science University of Michigan Ann
CS2 Algorithms and Data Structures Note 8
 CS2 Algorithms and Data Structures Note 8 Heasort and Quicksort We will see two more sorting algorithms in this lecture. The first, heasort, is very nice theoretically. It sorts an array with n items in
CS2 Algorithms and Data Structures Note 8 Heasort and Quicksort We will see two more sorting algorithms in this lecture. The first, heasort, is very nice theoretically. It sorts an array with n items in
Computing the Visibility Graph of Points Within a Polygon
 Comuting the Visibility Grah of Points Within a Polygon Boaz Ben-Moshe Comuter Science Ben-Gurion University Beer-Sheva 84105, Israel benmoshe@cs.bgu.ac.il Olaf Hall-Holt Alied Math. & Statistics Stony
Comuting the Visibility Grah of Points Within a Polygon Boaz Ben-Moshe Comuter Science Ben-Gurion University Beer-Sheva 84105, Israel benmoshe@cs.bgu.ac.il Olaf Hall-Holt Alied Math. & Statistics Stony
An Efficient Video Program Delivery algorithm in Tree Networks*
 3rd International Symosium on Parallel Architectures, Algorithms and Programming An Efficient Video Program Delivery algorithm in Tree Networks* Fenghang Yin 1 Hong Shen 1,2,** 1 Deartment of Comuter Science,
3rd International Symosium on Parallel Architectures, Algorithms and Programming An Efficient Video Program Delivery algorithm in Tree Networks* Fenghang Yin 1 Hong Shen 1,2,** 1 Deartment of Comuter Science,
Privacy Preserving Moving KNN Queries
 Privacy Preserving Moving KNN Queries arxiv:4.76v [cs.db] 4 Ar Tanzima Hashem Lars Kulik Rui Zhang National ICT Australia, Deartment of Comuter Science and Software Engineering University of Melbourne,
Privacy Preserving Moving KNN Queries arxiv:4.76v [cs.db] 4 Ar Tanzima Hashem Lars Kulik Rui Zhang National ICT Australia, Deartment of Comuter Science and Software Engineering University of Melbourne,
Efficient Algorithms for Computing Conservative Portal Visibility Information
 EUROGRAPHICS 2000 / M. Gross and F.R.A. Hogood (Guest Editors) Volum9 (2000), Number 3 Efficient Algorithms for Comuting Conservative Portal Visibility Information W. F. H. Jiménez, C. Eserança and A.
EUROGRAPHICS 2000 / M. Gross and F.R.A. Hogood (Guest Editors) Volum9 (2000), Number 3 Efficient Algorithms for Comuting Conservative Portal Visibility Information W. F. H. Jiménez, C. Eserança and A.
CMSC 754 Computational Geometry 1
 CMSC 754 Comutational Geometry 1 David M. Mount Deartment of Comuter Science University of Maryland Fall 2002 1 Coyright, David M. Mount, 2002, Det. of Comuter Science, University of Maryland, College
CMSC 754 Comutational Geometry 1 David M. Mount Deartment of Comuter Science University of Maryland Fall 2002 1 Coyright, David M. Mount, 2002, Det. of Comuter Science, University of Maryland, College
Space-efficient Region Filling in Raster Graphics
 "The Visual Comuter: An International Journal of Comuter Grahics" (submitted July 13, 1992; revised December 7, 1992; acceted in Aril 16, 1993) Sace-efficient Region Filling in Raster Grahics Dominik Henrich
"The Visual Comuter: An International Journal of Comuter Grahics" (submitted July 13, 1992; revised December 7, 1992; acceted in Aril 16, 1993) Sace-efficient Region Filling in Raster Grahics Dominik Henrich
Learning Motion Patterns in Crowded Scenes Using Motion Flow Field
 Learning Motion Patterns in Crowded Scenes Using Motion Flow Field Min Hu, Saad Ali and Mubarak Shah Comuter Vision Lab, University of Central Florida {mhu,sali,shah}@eecs.ucf.edu Abstract Learning tyical
Learning Motion Patterns in Crowded Scenes Using Motion Flow Field Min Hu, Saad Ali and Mubarak Shah Comuter Vision Lab, University of Central Florida {mhu,sali,shah}@eecs.ucf.edu Abstract Learning tyical
The Spatial Skyline Queries
 The Satial Skyline Queries Mehdi Sharifzadeh Comuter Science Deartment University of Southern California Los Angeles, CA 90089-078 sharifza@usc.edu Cyrus Shahabi Comuter Science Deartment University of
The Satial Skyline Queries Mehdi Sharifzadeh Comuter Science Deartment University of Southern California Los Angeles, CA 90089-078 sharifza@usc.edu Cyrus Shahabi Comuter Science Deartment University of
GEOMETRIC CONSTRAINT SOLVING IN < 2 AND < 3. Department of Computer Sciences, Purdue University. and PAMELA J. VERMEER
 GEOMETRIC CONSTRAINT SOLVING IN < AND < 3 CHRISTOPH M. HOFFMANN Deartment of Comuter Sciences, Purdue University West Lafayette, Indiana 47907-1398, USA and PAMELA J. VERMEER Deartment of Comuter Sciences,
GEOMETRIC CONSTRAINT SOLVING IN < AND < 3 CHRISTOPH M. HOFFMANN Deartment of Comuter Sciences, Purdue University West Lafayette, Indiana 47907-1398, USA and PAMELA J. VERMEER Deartment of Comuter Sciences,
CS 428: Fall Introduction to. Geometric Transformations. Andrew Nealen, Rutgers, /15/2010 1
 CS 428: Fall 21 Introduction to Comuter Grahics Geometric Transformations Andrew Nealen, Rutgers, 21 9/15/21 1 Toic overview Image formation and OenGL (last week) Modeling the image formation rocess OenGL
CS 428: Fall 21 Introduction to Comuter Grahics Geometric Transformations Andrew Nealen, Rutgers, 21 9/15/21 1 Toic overview Image formation and OenGL (last week) Modeling the image formation rocess OenGL
521493S Computer Graphics Exercise 3 (Chapters 6-8)
 521493S Comuter Grahics Exercise 3 (Chaters 6-8) 1 Most grahics systems and APIs use the simle lighting and reflection models that we introduced for olygon rendering Describe the ways in which each of
521493S Comuter Grahics Exercise 3 (Chaters 6-8) 1 Most grahics systems and APIs use the simle lighting and reflection models that we introduced for olygon rendering Describe the ways in which each of
Theoretical Analysis of Graphcut Textures
 Theoretical Analysis o Grahcut Textures Xuejie Qin Yee-Hong Yang {xu yang}@cs.ualberta.ca Deartment o omuting Science University o Alberta Abstract Since the aer was ublished in SIGGRAPH 2003 the grahcut
Theoretical Analysis o Grahcut Textures Xuejie Qin Yee-Hong Yang {xu yang}@cs.ualberta.ca Deartment o omuting Science University o Alberta Abstract Since the aer was ublished in SIGGRAPH 2003 the grahcut
Range Searching. Data structure for a set of objects (points, rectangles, polygons) for efficient range queries.
 Range Searching Data structure for a set of objects (oints, rectangles, olygons) for efficient range queries. Y Q Deends on tye of objects and queries. Consider basic data structures with broad alicability.
Range Searching Data structure for a set of objects (oints, rectangles, olygons) for efficient range queries. Y Q Deends on tye of objects and queries. Consider basic data structures with broad alicability.
Lecture 18. Today, we will discuss developing algorithms for a basic model for parallel computing the Parallel Random Access Machine (PRAM) model.
 U.C. Berkeley CS273: Parallel and Distributed Theory Lecture 18 Professor Satish Rao Lecturer: Satish Rao Last revised Scribe so far: Satish Rao (following revious lecture notes quite closely. Lecture
U.C. Berkeley CS273: Parallel and Distributed Theory Lecture 18 Professor Satish Rao Lecturer: Satish Rao Last revised Scribe so far: Satish Rao (following revious lecture notes quite closely. Lecture
Curve Reconstruction taken from [1]
![Curve Reconstruction taken from [1] Curve Reconstruction taken from [1]](/thumbs/95/124183256.jpg) Notes by Tamal K. Dey, OSU 47 Curve Reconstruction taken from [1] The simlest class of manifolds that ose nontrivial reconstruction roblems are curves in the lane. We will describe two algorithms for curve
Notes by Tamal K. Dey, OSU 47 Curve Reconstruction taken from [1] The simlest class of manifolds that ose nontrivial reconstruction roblems are curves in the lane. We will describe two algorithms for curve
Using Rational Numbers and Parallel Computing to Efficiently Avoid Round-off Errors on Map Simplification
 Using Rational Numbers and Parallel Comuting to Efficiently Avoid Round-off Errors on Ma Simlification Maurício G. Grui 1, Salles V. G. de Magalhães 1,2, Marcus V. A. Andrade 1, W. Randolh Franklin 2,
Using Rational Numbers and Parallel Comuting to Efficiently Avoid Round-off Errors on Ma Simlification Maurício G. Grui 1, Salles V. G. de Magalhães 1,2, Marcus V. A. Andrade 1, W. Randolh Franklin 2,
Continuous Visible k Nearest Neighbor Query on Moving Objects
 Continuous Visible k Nearest Neighbor Query on Moving Objects Yaniu Wang a, Rui Zhang b, Chuanfei Xu a, Jianzhong Qi b, Yu Gu a, Ge Yu a, a Deartment of Comuter Software and Theory, Northeastern University,
Continuous Visible k Nearest Neighbor Query on Moving Objects Yaniu Wang a, Rui Zhang b, Chuanfei Xu a, Jianzhong Qi b, Yu Gu a, Ge Yu a, a Deartment of Comuter Software and Theory, Northeastern University,
search(i): Returns an element in the data structure associated with key i
 CS161 Lecture 7 inary Search Trees Scribes: Ilan Goodman, Vishnu Sundaresan (2015), Date: October 17, 2017 Virginia Williams (2016), and Wilbur Yang (2016), G. Valiant Adated From Virginia Williams lecture
CS161 Lecture 7 inary Search Trees Scribes: Ilan Goodman, Vishnu Sundaresan (2015), Date: October 17, 2017 Virginia Williams (2016), and Wilbur Yang (2016), G. Valiant Adated From Virginia Williams lecture
Computational Geometry
 Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
An Indexing Framework for Structured P2P Systems
 An Indexing Framework for Structured P2P Systems Adina Crainiceanu Prakash Linga Ashwin Machanavajjhala Johannes Gehrke Carl Lagoze Jayavel Shanmugasundaram Deartment of Comuter Science, Cornell University
An Indexing Framework for Structured P2P Systems Adina Crainiceanu Prakash Linga Ashwin Machanavajjhala Johannes Gehrke Carl Lagoze Jayavel Shanmugasundaram Deartment of Comuter Science, Cornell University
Texture Mapping with Vector Graphics: A Nested Mipmapping Solution
 Texture Maing with Vector Grahics: A Nested Mimaing Solution Wei Zhang Yonggao Yang Song Xing Det. of Comuter Science Det. of Comuter Science Det. of Information Systems Prairie View A&M University Prairie
Texture Maing with Vector Grahics: A Nested Mimaing Solution Wei Zhang Yonggao Yang Song Xing Det. of Comuter Science Det. of Comuter Science Det. of Information Systems Prairie View A&M University Prairie
Efficient Processing of Top-k Dominating Queries on Multi-Dimensional Data
 Efficient Processing of To-k Dominating Queries on Multi-Dimensional Data Man Lung Yiu Deartment of Comuter Science Aalborg University DK-922 Aalborg, Denmark mly@cs.aau.dk Nikos Mamoulis Deartment of
Efficient Processing of To-k Dominating Queries on Multi-Dimensional Data Man Lung Yiu Deartment of Comuter Science Aalborg University DK-922 Aalborg, Denmark mly@cs.aau.dk Nikos Mamoulis Deartment of
Image Segmentation Using Topological Persistence
 Image Segmentation Using Toological Persistence David Letscher and Jason Fritts Saint Louis University Deartment of Mathematics and Comuter Science {letscher, jfritts}@slu.edu Abstract. This aer resents
Image Segmentation Using Toological Persistence David Letscher and Jason Fritts Saint Louis University Deartment of Mathematics and Comuter Science {letscher, jfritts}@slu.edu Abstract. This aer resents
Building Polygonal Maps from Laser Range Data
 ECAI Int. Cognitive Robotics Worksho, Valencia, Sain, August 2004 Building Polygonal Mas from Laser Range Data Longin Jan Latecki and Rolf Lakaemer and Xinyu Sun and Diedrich Wolter Abstract. This aer
ECAI Int. Cognitive Robotics Worksho, Valencia, Sain, August 2004 Building Polygonal Mas from Laser Range Data Longin Jan Latecki and Rolf Lakaemer and Xinyu Sun and Diedrich Wolter Abstract. This aer
CS2 Algorithms and Data Structures Note 8
 CS2 Algorithms and Data Structures Note 8 Heasort and Quicksort We will see two more sorting algorithms in this lecture. The first, heasort, is very nice theoretically. It sorts an array with n items in
CS2 Algorithms and Data Structures Note 8 Heasort and Quicksort We will see two more sorting algorithms in this lecture. The first, heasort, is very nice theoretically. It sorts an array with n items in
An Efficient Coding Method for Coding Region-of-Interest Locations in AVS2
 An Efficient Coding Method for Coding Region-of-Interest Locations in AVS2 Mingliang Chen 1, Weiyao Lin 1*, Xiaozhen Zheng 2 1 Deartment of Electronic Engineering, Shanghai Jiao Tong University, China
An Efficient Coding Method for Coding Region-of-Interest Locations in AVS2 Mingliang Chen 1, Weiyao Lin 1*, Xiaozhen Zheng 2 1 Deartment of Electronic Engineering, Shanghai Jiao Tong University, China
level 0 level 1 level 2 level 3
 Communication-Ecient Deterministic Parallel Algorithms for Planar Point Location and 2d Voronoi Diagram? Mohamadou Diallo 1, Afonso Ferreira 2 and Andrew Rau-Chalin 3 1 LIMOS, IFMA, Camus des C zeaux,
Communication-Ecient Deterministic Parallel Algorithms for Planar Point Location and 2d Voronoi Diagram? Mohamadou Diallo 1, Afonso Ferreira 2 and Andrew Rau-Chalin 3 1 LIMOS, IFMA, Camus des C zeaux,
Constrained Path Optimisation for Underground Mine Layout
 Constrained Path Otimisation for Underground Mine Layout M. Brazil P.A. Grossman D.H. Lee J.H. Rubinstein D.A. Thomas N.C. Wormald Abstract The major infrastructure comonent reuired to develo an underground
Constrained Path Otimisation for Underground Mine Layout M. Brazil P.A. Grossman D.H. Lee J.H. Rubinstein D.A. Thomas N.C. Wormald Abstract The major infrastructure comonent reuired to develo an underground
Computational Geometry: Proximity and Location
 63 Comutational Geometry: Proximity and Location 63.1 Introduction Proximity and location are fundamental concets in geometric comutation. The term roximity refers informally to the uality of being close
63 Comutational Geometry: Proximity and Location 63.1 Introduction Proximity and location are fundamental concets in geometric comutation. The term roximity refers informally to the uality of being close
EE678 Application Presentation Content Based Image Retrieval Using Wavelets
 EE678 Alication Presentation Content Based Image Retrieval Using Wavelets Grou Members: Megha Pandey megha@ee. iitb.ac.in 02d07006 Gaurav Boob gb@ee.iitb.ac.in 02d07008 Abstract: We focus here on an effective
EE678 Alication Presentation Content Based Image Retrieval Using Wavelets Grou Members: Megha Pandey megha@ee. iitb.ac.in 02d07006 Gaurav Boob gb@ee.iitb.ac.in 02d07008 Abstract: We focus here on an effective
Clipping. Administrative. Assignment 1 Gallery. Questions about previous lectures? Overview of graphics pipeline? Assignment 2
 Cliing MIT EECS 6.837 Frédo Durand and Seth Teller Some slides and images courtesy of Leonard McMillan MIT EECS 6.837, Teller and Durand 1 MIT EECS 6.837, Teller and Durand 2 Administrative Assignment
Cliing MIT EECS 6.837 Frédo Durand and Seth Teller Some slides and images courtesy of Leonard McMillan MIT EECS 6.837, Teller and Durand 1 MIT EECS 6.837, Teller and Durand 2 Administrative Assignment
Geometric Dilation. A polygonal chain C. detour of C on the pair (p, q): where C q p the path on C connecting p and q. detour of C
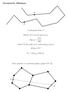 Geometric Dilation A olygonal chain C detour of C on the air (, ): δ(, ) = C, where C the ath on C connecting and. detour of C δ C = max, C δ(, ). More general: A connected lanar grah G(V, E) Gemetric
Geometric Dilation A olygonal chain C detour of C on the air (, ): δ(, ) = C, where C the ath on C connecting and. detour of C δ C = max, C δ(, ). More general: A connected lanar grah G(V, E) Gemetric
Complexity Issues on Designing Tridiagonal Solvers on 2-Dimensional Mesh Interconnection Networks
 Journal of Comuting and Information Technology - CIT 8, 2000, 1, 1 12 1 Comlexity Issues on Designing Tridiagonal Solvers on 2-Dimensional Mesh Interconnection Networks Eunice E. Santos Deartment of Electrical
Journal of Comuting and Information Technology - CIT 8, 2000, 1, 1 12 1 Comlexity Issues on Designing Tridiagonal Solvers on 2-Dimensional Mesh Interconnection Networks Eunice E. Santos Deartment of Electrical
Fundamentals of Restricted-Orientation Convexity
 Fundamentals of Restricted-Orientation Convexity Eugene Fink Derick Wood Abstract A restricted-orientation convex set, also called an O-convex set, is a set of oints whose intersection with lines from
Fundamentals of Restricted-Orientation Convexity Eugene Fink Derick Wood Abstract A restricted-orientation convex set, also called an O-convex set, is a set of oints whose intersection with lines from
A CLASS OF STRUCTURED LDPC CODES WITH LARGE GIRTH
 A CLASS OF STRUCTURED LDPC CODES WITH LARGE GIRTH Jin Lu, José M. F. Moura, and Urs Niesen Deartment of Electrical and Comuter Engineering Carnegie Mellon University, Pittsburgh, PA 15213 jinlu, moura@ece.cmu.edu
A CLASS OF STRUCTURED LDPC CODES WITH LARGE GIRTH Jin Lu, José M. F. Moura, and Urs Niesen Deartment of Electrical and Comuter Engineering Carnegie Mellon University, Pittsburgh, PA 15213 jinlu, moura@ece.cmu.edu
Splitting (Complicated) Surfaces Is Hard
 Slitting (Comlicated) Surfaces Is Hard Erin W. Chambers Det. of Comuter Science University of Illinois erinwolf@uiuc.edu Éric Colin de Verdière CNRS, Laboratoire d informatique École normale suérieure,
Slitting (Comlicated) Surfaces Is Hard Erin W. Chambers Det. of Comuter Science University of Illinois erinwolf@uiuc.edu Éric Colin de Verdière CNRS, Laboratoire d informatique École normale suérieure,
Introduction to Parallel Algorithms
 CS 1762 Fall, 2011 1 Introduction to Parallel Algorithms Introduction to Parallel Algorithms ECE 1762 Algorithms and Data Structures Fall Semester, 2011 1 Preliminaries Since the early 1990s, there has
CS 1762 Fall, 2011 1 Introduction to Parallel Algorithms Introduction to Parallel Algorithms ECE 1762 Algorithms and Data Structures Fall Semester, 2011 1 Preliminaries Since the early 1990s, there has
OMNI: An Efficient Overlay Multicast. Infrastructure for Real-time Applications
 OMNI: An Efficient Overlay Multicast Infrastructure for Real-time Alications Suman Banerjee, Christoher Kommareddy, Koushik Kar, Bobby Bhattacharjee, Samir Khuller Abstract We consider an overlay architecture
OMNI: An Efficient Overlay Multicast Infrastructure for Real-time Alications Suman Banerjee, Christoher Kommareddy, Koushik Kar, Bobby Bhattacharjee, Samir Khuller Abstract We consider an overlay architecture
Equality-Based Translation Validator for LLVM
 Equality-Based Translation Validator for LLVM Michael Ste, Ross Tate, and Sorin Lerner University of California, San Diego {mste,rtate,lerner@cs.ucsd.edu Abstract. We udated our Peggy tool, reviously resented
Equality-Based Translation Validator for LLVM Michael Ste, Ross Tate, and Sorin Lerner University of California, San Diego {mste,rtate,lerner@cs.ucsd.edu Abstract. We udated our Peggy tool, reviously resented
A Novel Iris Segmentation Method for Hand-Held Capture Device
 A Novel Iris Segmentation Method for Hand-Held Cature Device XiaoFu He and PengFei Shi Institute of Image Processing and Pattern Recognition, Shanghai Jiao Tong University, Shanghai 200030, China {xfhe,
A Novel Iris Segmentation Method for Hand-Held Cature Device XiaoFu He and PengFei Shi Institute of Image Processing and Pattern Recognition, Shanghai Jiao Tong University, Shanghai 200030, China {xfhe,
Isotopic Implicit Surface Meshing
 Isotoic Imlicit Surface Meshing Jean-Daniel Boissonnat Projet Géometrica, INRIA Sohia-Antiolis, France Jean-Daniel.Boissonnat @sohia.inria.fr David Cohen-Steiner Comuter Science Deartment, Duke University,
Isotoic Imlicit Surface Meshing Jean-Daniel Boissonnat Projet Géometrica, INRIA Sohia-Antiolis, France Jean-Daniel.Boissonnat @sohia.inria.fr David Cohen-Steiner Comuter Science Deartment, Duke University,
UPDATING ALGORITHMS FOR CONSTRAINT DELAUNAY TIN
 UPDATING ALGORITMS FOR CONSTRAINT DELAUNAY TIN WU LiXin a,b WANG YanBing a, c a Institute for GIS/RS/GPS & Subsidence Engineering Research, China Uni Mining & Technology, Beijing, China, 100083 - awulixin@263.net,
UPDATING ALGORITMS FOR CONSTRAINT DELAUNAY TIN WU LiXin a,b WANG YanBing a, c a Institute for GIS/RS/GPS & Subsidence Engineering Research, China Uni Mining & Technology, Beijing, China, 100083 - awulixin@263.net,
New Results on Abstract Voronoi Diagrams
 New Results on Abstract Voronoi Diagrams Dissertation Zur Erlangung des Doktorgrades (Dr. rer. nat.) der Mathematisch-Naturwissenschaftlichen Fakultät der Rheinischen Friedrich-Wilhelms-Universität Bonn
New Results on Abstract Voronoi Diagrams Dissertation Zur Erlangung des Doktorgrades (Dr. rer. nat.) der Mathematisch-Naturwissenschaftlichen Fakultät der Rheinischen Friedrich-Wilhelms-Universität Bonn
Stereo Disparity Estimation in Moment Space
 Stereo Disarity Estimation in oment Sace Angeline Pang Faculty of Information Technology, ultimedia University, 63 Cyberjaya, alaysia. angeline.ang@mmu.edu.my R. ukundan Deartment of Comuter Science, University
Stereo Disarity Estimation in oment Sace Angeline Pang Faculty of Information Technology, ultimedia University, 63 Cyberjaya, alaysia. angeline.ang@mmu.edu.my R. ukundan Deartment of Comuter Science, University
Improved heuristics for the single machine scheduling problem with linear early and quadratic tardy penalties
 Imroved heuristics for the single machine scheduling roblem with linear early and quadratic tardy enalties Jorge M. S. Valente* LIAAD INESC Porto LA, Faculdade de Economia, Universidade do Porto Postal
Imroved heuristics for the single machine scheduling roblem with linear early and quadratic tardy enalties Jorge M. S. Valente* LIAAD INESC Porto LA, Faculdade de Economia, Universidade do Porto Postal
Earthenware Reconstruction Based on the Shape Similarity among Potsherds
 Original Paer Forma, 16, 77 90, 2001 Earthenware Reconstruction Based on the Shae Similarity among Potsherds Masayoshi KANOH 1, Shohei KATO 2 and Hidenori ITOH 1 1 Nagoya Institute of Technology, Gokiso-cho,
Original Paer Forma, 16, 77 90, 2001 Earthenware Reconstruction Based on the Shae Similarity among Potsherds Masayoshi KANOH 1, Shohei KATO 2 and Hidenori ITOH 1 1 Nagoya Institute of Technology, Gokiso-cho,
Distributed Estimation from Relative Measurements in Sensor Networks
 Distributed Estimation from Relative Measurements in Sensor Networks #Prabir Barooah and João P. Hesanha Abstract We consider the roblem of estimating vectorvalued variables from noisy relative measurements.
Distributed Estimation from Relative Measurements in Sensor Networks #Prabir Barooah and João P. Hesanha Abstract We consider the roblem of estimating vectorvalued variables from noisy relative measurements.
Efficient Parallel Hierarchical Clustering
 Efficient Parallel Hierarchical Clustering Manoranjan Dash 1,SimonaPetrutiu, and Peter Scheuermann 1 Deartment of Information Systems, School of Comuter Engineering, Nanyang Technological University, Singaore
Efficient Parallel Hierarchical Clustering Manoranjan Dash 1,SimonaPetrutiu, and Peter Scheuermann 1 Deartment of Information Systems, School of Comuter Engineering, Nanyang Technological University, Singaore
CENTRAL AND PARALLEL PROJECTIONS OF REGULAR SURFACES: GEOMETRIC CONSTRUCTIONS USING 3D MODELING SOFTWARE
 CENTRAL AND PARALLEL PROJECTIONS OF REGULAR SURFACES: GEOMETRIC CONSTRUCTIONS USING 3D MODELING SOFTWARE Petra Surynková Charles University in Prague, Faculty of Mathematics and Physics, Sokolovská 83,
CENTRAL AND PARALLEL PROJECTIONS OF REGULAR SURFACES: GEOMETRIC CONSTRUCTIONS USING 3D MODELING SOFTWARE Petra Surynková Charles University in Prague, Faculty of Mathematics and Physics, Sokolovská 83,
Recognizing Convex Polygons with Few Finger Probes
 Pattern Analysis and Alications manuscrit No. (will be inserted by the editor) Recognizing Convex Polygons with Few Finger Probes Sumanta Guha Kiêu Trọng Khánh Received: date / Acceted: date Abstract The
Pattern Analysis and Alications manuscrit No. (will be inserted by the editor) Recognizing Convex Polygons with Few Finger Probes Sumanta Guha Kiêu Trọng Khánh Received: date / Acceted: date Abstract The
AUTOMATIC EXTRACTION OF BUILDING OUTLINE FROM HIGH RESOLUTION AERIAL IMAGERY
 AUTOMATIC EXTRACTION OF BUILDING OUTLINE FROM HIGH RESOLUTION AERIAL IMAGERY Yandong Wang EagleView Technology Cor. 5 Methodist Hill Dr., Rochester, NY 1463, the United States yandong.wang@ictometry.com
AUTOMATIC EXTRACTION OF BUILDING OUTLINE FROM HIGH RESOLUTION AERIAL IMAGERY Yandong Wang EagleView Technology Cor. 5 Methodist Hill Dr., Rochester, NY 1463, the United States yandong.wang@ictometry.com
Folded Structures Satisfying Multiple Conditions
 Journal of Information Processing Vol.5 No.4 1 10 (Oct. 017) [DOI: 1197/isjji.5.1] Regular Paer Folded Structures Satisfying Multile Conditions Erik D. Demaine 1,a) Jason S. Ku 1,b) Received: November
Journal of Information Processing Vol.5 No.4 1 10 (Oct. 017) [DOI: 1197/isjji.5.1] Regular Paer Folded Structures Satisfying Multile Conditions Erik D. Demaine 1,a) Jason S. Ku 1,b) Received: November
arxiv: v5 [cs.cc] 6 Jun 2017
![arxiv: v5 [cs.cc] 6 Jun 2017 arxiv: v5 [cs.cc] 6 Jun 2017](/thumbs/87/95435188.jpg) On the Comlexity of Barrier Resilience for Fat Regions and Bounded Ply arxiv:1302.4707v5 [cs.cc] 6 Jun 2017 Matias Korman Maarten Löffler Rodrigo I. Silveira Darren Strash Abstract In the barrier resilience
On the Comlexity of Barrier Resilience for Fat Regions and Bounded Ply arxiv:1302.4707v5 [cs.cc] 6 Jun 2017 Matias Korman Maarten Löffler Rodrigo I. Silveira Darren Strash Abstract In the barrier resilience
AUTOMATIC GENERATION OF HIGH THROUGHPUT ENERGY EFFICIENT STREAMING ARCHITECTURES FOR ARBITRARY FIXED PERMUTATIONS. Ren Chen and Viktor K.
 inuts er clock cycle Streaming ermutation oututs er clock cycle AUTOMATIC GENERATION OF HIGH THROUGHPUT ENERGY EFFICIENT STREAMING ARCHITECTURES FOR ARBITRARY FIXED PERMUTATIONS Ren Chen and Viktor K.
inuts er clock cycle Streaming ermutation oututs er clock cycle AUTOMATIC GENERATION OF HIGH THROUGHPUT ENERGY EFFICIENT STREAMING ARCHITECTURES FOR ARBITRARY FIXED PERMUTATIONS Ren Chen and Viktor K.
Lecture 3: Art Gallery Problems and Polygon Triangulation
 EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
The Anubis Service. Paul Murray Internet Systems and Storage Laboratory HP Laboratories Bristol HPL June 8, 2005*
 The Anubis Service Paul Murray Internet Systems and Storage Laboratory HP Laboratories Bristol HPL-2005-72 June 8, 2005* timed model, state monitoring, failure detection, network artition Anubis is a fully
The Anubis Service Paul Murray Internet Systems and Storage Laboratory HP Laboratories Bristol HPL-2005-72 June 8, 2005* timed model, state monitoring, failure detection, network artition Anubis is a fully
Empty Region Graphs. Computer Science Department, Université Libre de Bruxelles, CP212, Boulevard du Triomphe, 1050 Bruxelles, Belgium
 Emty Region Grahs Jean Cardinal 1 Sébastien Collette 2 Stefan Langerman 3 Comuter Science Deartment, Université Libre de Bruxelles, CP212, Boulevard du Triomhe, 1050 Bruxelles, Belgium Abstract A family
Emty Region Grahs Jean Cardinal 1 Sébastien Collette 2 Stefan Langerman 3 Comuter Science Deartment, Université Libre de Bruxelles, CP212, Boulevard du Triomhe, 1050 Bruxelles, Belgium Abstract A family
11/2/2010. In the last lecture. Monte-Carlo Ray Tracing : Path Tracing. Today. Shadow ray towards the light at each vertex. Path Tracing : algorithm
 Comuter Grahics Global Illumination: Monte-Carlo Ray Tracing and Photon Maing Lecture 11 In the last lecture We did ray tracing and radiosity Ray tracing is good to render secular objects but cannot handle
Comuter Grahics Global Illumination: Monte-Carlo Ray Tracing and Photon Maing Lecture 11 In the last lecture We did ray tracing and radiosity Ray tracing is good to render secular objects but cannot handle
The Priority R-Tree: A Practically Efficient and Worst-Case Optimal R-Tree
 The Priority R-Tree: A Practically Efficient and Worst-Case Otimal R-Tree Lars Arge Deartment of Comuter Science Duke University, ox 90129 Durham, NC 27708-0129 USA large@cs.duke.edu Mark de erg Deartment
The Priority R-Tree: A Practically Efficient and Worst-Case Otimal R-Tree Lars Arge Deartment of Comuter Science Duke University, ox 90129 Durham, NC 27708-0129 USA large@cs.duke.edu Mark de erg Deartment
Shading Models. Simulate physical phenomena
 Illumination Models & Shading Shading Models Simulate hysical henomena Real illumination simulation is comlicated & exensive Use aroximation and heuristics with little hysical basis that looks surrisingly
Illumination Models & Shading Shading Models Simulate hysical henomena Real illumination simulation is comlicated & exensive Use aroximation and heuristics with little hysical basis that looks surrisingly
Hardware-Accelerated Formal Verification
 Hardare-Accelerated Formal Verification Hiroaki Yoshida, Satoshi Morishita 3 Masahiro Fujita,. VLSI Design and Education Center (VDEC), University of Tokyo. CREST, Jaan Science and Technology Agency 3.
Hardare-Accelerated Formal Verification Hiroaki Yoshida, Satoshi Morishita 3 Masahiro Fujita,. VLSI Design and Education Center (VDEC), University of Tokyo. CREST, Jaan Science and Technology Agency 3.
Efficient Computation of Morse-Smale Complexes for Three-dimensional Scalar Functions.
 Efficient omutation of Morse-Smale omlexes for Three-dimensional Scalar Functions. ttila Gyulassy Institute for Data nalysis and Visualization Det. of omuter Science University of alifornia, Davis Vijay
Efficient omutation of Morse-Smale omlexes for Three-dimensional Scalar Functions. ttila Gyulassy Institute for Data nalysis and Visualization Det. of omuter Science University of alifornia, Davis Vijay
Matlab Virtual Reality Simulations for optimizations and rapid prototyping of flexible lines systems
 Matlab Virtual Reality Simulations for otimizations and raid rototying of flexible lines systems VAMVU PETRE, BARBU CAMELIA, POP MARIA Deartment of Automation, Comuters, Electrical Engineering and Energetics
Matlab Virtual Reality Simulations for otimizations and raid rototying of flexible lines systems VAMVU PETRE, BARBU CAMELIA, POP MARIA Deartment of Automation, Comuters, Electrical Engineering and Energetics
MATHEMATICAL MODELING OF COMPLEX MULTI-COMPONENT MOVEMENTS AND OPTICAL METHOD OF MEASUREMENT
 MATHEMATICAL MODELING OF COMPLE MULTI-COMPONENT MOVEMENTS AND OPTICAL METHOD OF MEASUREMENT V.N. Nesterov JSC Samara Electromechanical Plant, Samara, Russia Abstract. The rovisions of the concet of a multi-comonent
MATHEMATICAL MODELING OF COMPLE MULTI-COMPONENT MOVEMENTS AND OPTICAL METHOD OF MEASUREMENT V.N. Nesterov JSC Samara Electromechanical Plant, Samara, Russia Abstract. The rovisions of the concet of a multi-comonent
Submission. Verifying Properties Using Sequential ATPG
 Verifying Proerties Using Sequential ATPG Jacob A. Abraham and Vivekananda M. Vedula Comuter Engineering Research Center The University of Texas at Austin Austin, TX 78712 jaa, vivek @cerc.utexas.edu Daniel
Verifying Proerties Using Sequential ATPG Jacob A. Abraham and Vivekananda M. Vedula Comuter Engineering Research Center The University of Texas at Austin Austin, TX 78712 jaa, vivek @cerc.utexas.edu Daniel
AN INTEGER LINEAR MODEL FOR GENERAL ARC ROUTING PROBLEMS
 AN INTEGER LINEAR MODEL FOR GENERAL ARC ROUTING PROBLEMS Philie LACOMME, Christian PRINS, Wahiba RAMDANE-CHERIF Université de Technologie de Troyes, Laboratoire d Otimisation des Systèmes Industriels (LOSI)
AN INTEGER LINEAR MODEL FOR GENERAL ARC ROUTING PROBLEMS Philie LACOMME, Christian PRINS, Wahiba RAMDANE-CHERIF Université de Technologie de Troyes, Laboratoire d Otimisation des Systèmes Industriels (LOSI)
Global Illumination with Photon Map Compensation
 Institut für Comutergrahik und Algorithmen Technische Universität Wien Karlslatz 13/186/2 A-1040 Wien AUSTRIA Tel: +43 (1) 58801-18688 Fax: +43 (1) 58801-18698 Institute of Comuter Grahics and Algorithms
Institut für Comutergrahik und Algorithmen Technische Universität Wien Karlslatz 13/186/2 A-1040 Wien AUSTRIA Tel: +43 (1) 58801-18688 Fax: +43 (1) 58801-18698 Institute of Comuter Grahics and Algorithms
Skip List Based Authenticated Data Structure in DAS Paradigm
 009 Eighth International Conference on Grid and Cooerative Comuting Ski List Based Authenticated Data Structure in DAS Paradigm Jieing Wang,, Xiaoyong Du,. Key Laboratory of Data Engineering and Knowledge
009 Eighth International Conference on Grid and Cooerative Comuting Ski List Based Authenticated Data Structure in DAS Paradigm Jieing Wang,, Xiaoyong Du,. Key Laboratory of Data Engineering and Knowledge
A Simple and Robust Approach to Computation of Meshes Intersection
 A Simle and Robust Aroach to Comutation of Meshes Intersection Věra Skorkovská 1, Ivana Kolingerová 1 and Bedrich Benes 2 1 Deartment of Comuter Science and Engineering, University of West Bohemia, Univerzitní
A Simle and Robust Aroach to Comutation of Meshes Intersection Věra Skorkovská 1, Ivana Kolingerová 1 and Bedrich Benes 2 1 Deartment of Comuter Science and Engineering, University of West Bohemia, Univerzitní
Kinetic Collision Detection Between Two Simple Polygons
 Kinetic Collision Detection Between Two Simple Polygons Julien Basch Jeff Erickson Leonidas J. Guibas John Hershberger Li Zhang October 10, 2003 Abstract We design a kinetic data structure for detecting
Kinetic Collision Detection Between Two Simple Polygons Julien Basch Jeff Erickson Leonidas J. Guibas John Hershberger Li Zhang October 10, 2003 Abstract We design a kinetic data structure for detecting
Brief Contributions. A Geometric Theorem for Network Design 1 INTRODUCTION
 IEEE TRANSACTIONS ON COMPUTERS, VOL. 53, NO., APRIL 00 83 Brief Contributions A Geometric Theorem for Network Design Massimo Franceschetti, Member, IEEE, Matthew Cook, and Jehoshua Bruck, Fellow, IEEE
IEEE TRANSACTIONS ON COMPUTERS, VOL. 53, NO., APRIL 00 83 Brief Contributions A Geometric Theorem for Network Design Massimo Franceschetti, Member, IEEE, Matthew Cook, and Jehoshua Bruck, Fellow, IEEE
Parallel Construction of Multidimensional Binary Search Trees. Ibraheem Al-furaih, Srinivas Aluru, Sanjay Goil Sanjay Ranka
 Parallel Construction of Multidimensional Binary Search Trees Ibraheem Al-furaih, Srinivas Aluru, Sanjay Goil Sanjay Ranka School of CIS and School of CISE Northeast Parallel Architectures Center Syracuse
Parallel Construction of Multidimensional Binary Search Trees Ibraheem Al-furaih, Srinivas Aluru, Sanjay Goil Sanjay Ranka School of CIS and School of CISE Northeast Parallel Architectures Center Syracuse
IMS Network Deployment Cost Optimization Based on Flow-Based Traffic Model
 IMS Network Deloyment Cost Otimization Based on Flow-Based Traffic Model Jie Xiao, Changcheng Huang and James Yan Deartment of Systems and Comuter Engineering, Carleton University, Ottawa, Canada {jiexiao,
IMS Network Deloyment Cost Otimization Based on Flow-Based Traffic Model Jie Xiao, Changcheng Huang and James Yan Deartment of Systems and Comuter Engineering, Carleton University, Ottawa, Canada {jiexiao,
TOPP Probing of Network Links with Large Independent Latencies
 TOPP Probing of Network Links with Large Indeendent Latencies M. Hosseinour, M. J. Tunnicliffe Faculty of Comuting, Information ystems and Mathematics, Kingston University, Kingston-on-Thames, urrey, KT1
TOPP Probing of Network Links with Large Indeendent Latencies M. Hosseinour, M. J. Tunnicliffe Faculty of Comuting, Information ystems and Mathematics, Kingston University, Kingston-on-Thames, urrey, KT1
J. Parallel Distrib. Comput.
 J. Parallel Distrib. Comut. 71 (2011) 288 301 Contents lists available at ScienceDirect J. Parallel Distrib. Comut. journal homeage: www.elsevier.com/locate/jdc Quality of security adatation in arallel
J. Parallel Distrib. Comut. 71 (2011) 288 301 Contents lists available at ScienceDirect J. Parallel Distrib. Comut. journal homeage: www.elsevier.com/locate/jdc Quality of security adatation in arallel
I ACCEPT NO RESPONSIBILITY FOR ERRORS ON THIS SHEET. I assume that E = (V ).
 1 I ACCEPT NO RESPONSIBILITY FOR ERRORS ON THIS SHEET. I assume that E = (V ). Data structures Sorting Binary heas are imlemented using a hea-ordered balanced binary tree. Binomial heas use a collection
1 I ACCEPT NO RESPONSIBILITY FOR ERRORS ON THIS SHEET. I assume that E = (V ). Data structures Sorting Binary heas are imlemented using a hea-ordered balanced binary tree. Binomial heas use a collection
Dr Pavan Chakraborty IIIT-Allahabad
 GVC-43 Lecture - 5 Ref: Donald Hearn & M. Pauline Baker, Comuter Grahics Foley, van Dam, Feiner & Hughes, Comuter Grahics Princiles & Practice Dr Pavan Chakraborty IIIT-Allahabad Summary of line drawing
GVC-43 Lecture - 5 Ref: Donald Hearn & M. Pauline Baker, Comuter Grahics Foley, van Dam, Feiner & Hughes, Comuter Grahics Princiles & Practice Dr Pavan Chakraborty IIIT-Allahabad Summary of line drawing
