Curve Reconstruction taken from [1]

Transcription

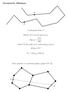
1 Notes by Tamal K. Dey, OSU 47 Curve Reconstruction taken from [1] The simlest class of manifolds that ose nontrivial reconstruction roblems are curves in the lane. We will describe two algorithms for curve reconstruction, CRUST and NN-CRUST in this chater. First, we will develo some general results that will be alied to rove the correctness of the both algorithms. A single curve in the lane is defined by a maξ : [0, 1] R 2 where [0, 1] is the closed interval between 0 and 1 on the real line. The function ξ is one-to-one everywhere excet at the endoints whereξ(0)=ξ(1). The curve is C 1 -smooth ifξhas a continuous non-zero first derivative in the interior of [0, 1] and the right derivative at 0 is same as the left derivative at 1 both being non-zero. Ifξ has continuous ith derivatives at each oint as well, the curve is called C i -smooth. When we refer to a curveσin the lane, we actually mean the image of one or more such mas. By definition Σ does not self-intersect though it can have multile comonents each of which is a closed curve, i.e., without any end oint. For a finite samle to be an ε-samle for some ε > 0, it is essential that the local feature size f is ositive everywhere. While this is true for all C 2 -smooth curves, there are C 1 -smooth curves with zero local feature size at some oint. For examle, consider the curve y= x 4 3 for 1 x 1 and join the endoints ( 1, 1) and (1, 1) with a smooth curve. This curve is C 1 -smooth at (0, 0) and its medial axis asses through the oint (0, 0). Therefore, the local feature size is zero at (0, 0). We learnt that C 1 -smooth curves do not necessarily have ositive minimum local feature size while C 2 -smooth curves do. Are there curves in between C 1 - and C 2 -smooth classes with ositive local feature size everywhere? Indeed, there is a class called C 1,1 -smooth curves with this roerty. These curves are C 1 -smooth and have normals satisfying a Lischitz continuity roerty. To avoid confusions about narrowing down the class, we exlicitly assume that Σ has strictly ositive local feature size everywhere. For any two oints x, y inσdefine two curve segments,γ(x, y) andγ (x, y) between x and y, i.e.,σ=γ(x, y) γ (x, y) andγ(x, y) γ (x, y)={x, y}. Let P be a set of samle oints fromσ. We say a curve segment is emty if its interior does not contain any oint from P. An edge connecting two samle oints, say and q, is called correct if eitherγ(, q) orγ (, q) is emty. In other words, and q are two consecutive samle oints onσ. Any edge that is not correct is called incorrect. The goal of curve reconstruction is to comute a iecewise linear curve consisting of all and only correct edges. In Figure 27(b) all solid edges are correct and dotted edges are incorrect. We will describe CRUST in Section 21 and NN-CRUST in Section 22. Some general results are resented in Subsection 20 which are used later to claim the correctness of the algorithms. 20 Consequences ofε-samling Let P be anε-samle ofσ. For sufficiently smallε>0, several roerties can be roved.

2 48 Notes by Tamal K. Dey, OSU (a) (b) Figure 27: (a) A smooth curve, (b) its reconstruction from a samle shown with solid edges. Lemma 14 (Emty Segment.). Let P and x Σ so thatγ(, x) is emty. Let the erendicular bisector of x intersect the emty segmentγ(, x) at z. Ifε<1then (i) the ball B z, z intersectsσonly inγ(, x), (ii) the ball B z, z is emty, and (iii) z ε f (z). PROOF. Let B= B z, z andγ=γ(, x). Suose B Σ γ, see Figure 28. Shrink B continuously centering z until Int B Σ becomes a 1-ball and it is tangent to some other oint ofσ. Let B be the shrunken ball. The ball B exists as B z,δ Σ is a 1-ball for some sufficiently smallδ>0 and B Σ is not a 1-ball. The ball B is emty of any samle oint as Int B intersectsσonly in a subset ofγwhich is emty. But, since B Σ is not a 1-ball, it contains a medial axis oint by the Feature Ball Lemma 11. Thus, its radius is at least f (z). The oint z does not have any samle oint within f (z) distance as B is emty. This contradicts that P is anε-samle ofσwhereε<1. Therefore, B intersectsσonly inγ(, x) comleting the roof of (i). Proerty (ii) follows immediately asγ(, x) is emty and B intersectsσonly inγ(, x). By ε-samling, the nearest samle oint to z is withinε f (z) distance establishing (iii). B γ z B x γ z x Figure 28: Illustration for the Emty Segment Lemma 14. The icture on the left is imossible while the one on the right is correct. The Emty Segment Lemma 14 imlies that oints in an emty segment are close and any correct edge is Delaunay whenεis small.

3 Notes by Tamal K. Dey, OSU 49 Lemma 15 (Small Segment.). Let x, y be any two oints so thatγ(x, y) is emty. Then x y f (x) forε<1. 2ε PROOF. Sinceγ(x, y) is emty, it is a subset of an emty segmentγ(, q) for two samle oints and q. Let z be the oint where the erendicular bisector of q meetsγ(, q). Consider the ball B= B z, z. Sinceγ(, q) is emty, the ball B has the roerties stated in the Emty Segment Lemma 14. Since B containsγ(, q), both x and y are in B. Therefore, z x ε f (z) by the ε-samling condition. By the Feature Translation Lemma 13 f (z) f (x). We have x y 2 z 2ε f (z) 2ε f (x). Lemma 16 (Small Edge.). Let q be a correct edge. Forε<1, (i) q 2ε f () and (ii) q is Delaunay. PROOF. Any correct edge q has the roerty that eitherγ(q, ) orγ(, q) is emty. Therefore, (i) is immediate from the Small Segment Lemma 15. It follows from roerty (ii) of the Emty Segment Lemma 14 that there exists an emty ball circumscribing the correct edge q roving (ii). If three oints x, y, and z onσare sufficiently close, the segments xy and yz make small angles with the tangent at y. This imlies that the angle xyz is close toπ. As a corollary two adjacent correct edges make an angle close toπ. Lemma 17 (Segment Angle.). Let x, y, and z be three oints onσwith x y and y z being no more than 2ε f (y) forε< 1 2. Letαbe the angle between the tangent toσat y and the line segment yz. One has (i)α arcsin ε and (ii) xyz π 2 arcsin ε. PROOF. Consider the two medial balls sandwichingσat y as in Figure 29. Letαbe the angle between the tangent at y and the segment yz. Since z lies outside the medial balls, the length of the segment yz is no more than that of yz where z is the oint of intersection of yz and a medial ball as shown. In that case,

4 50 Notes by Tamal K. Dey, OSU α Σ x y α z z m Figure 29: Illustration for the Segment Angle Lemma 17. (( y z ) α arcsin 2 (( y z = arcsin 2 ) / ( m y ) ) ) / ( m y ) It is given that y z 2ε f (y) whereε< 1 2. Also, m y f (y) since m is a medial axis oint. Plugging in these values we get ε α arcsin comleting the roof of (i). We have myz π 2 α myz π 2 arcsin ε. Similarly it can be shown that myx π 2 arcsin ε. Proerty (ii) follows immediately as xyz= myz+ myx. Since any correct edge q has a length no more than 2ε f () forε<1 (Small Edge Lemma 16), we have the following result. Lemma 18 (Edge Angle.). Let q and r be two correct edges incident to. We have qr π 2 arcsin ε forε< Crust We have already seen that all correct edges connecting consecutive samle oints in anε-samle are resent in the Delaunay triangulation of the samle oints if ε < 1. The main algorithmic.

5 Notes by Tamal K. Dey, OSU 51 challenge is to distinguish these edges from the rest of the Delaunay edges. The CRUST algorithm achieves this by observing some roerties of the Voronoi vertices. Figure 30: Voronoi vertices aroximate the medial axis of a curve in the lane. The Voronoi vertices are shown with hollow circles in the right icture Algorithm Consider Figure 30. The left icture shows the Voronoi diagram clied within a box for a dense samle of a curve. The icture on the right shows the Voronoi vertices searately. A careful observation reveals that the Voronoi vertices lie near the medial axis of the curve (Exercise 8). The CRUST algorithm exloits this fact. All emty balls circumscribing incorrect edges in Del P cross the medial axis and hence contain Voronoi vertices inside. Therefore, they cannot aear in the Delaunay triangulation of P V where V is the set of Voronoi vertices in Vor P. On the other hand, all correct edges still survive in Del (P V). So, the algorithm first comutes Vor P and then comutes the Delaunay triangulation of P V where V is the set of Voronoi vertices of Vor P. The Delaunay edges of Del (P V) that connect two oints in P are outut. It is roved that an edge is outut if and only if it is correct. CRUST(P) 1 comute Vor P; 2 let V be the Voronoi vertices of Vor P; 3 comute Del (P V); 4 E := ; 5 for each edge q Del (P V)do 6 if P and q P 7 E := E q; 8 endif 9 outut E.

6 52 Notes by Tamal K. Dey, OSU The Voronoi and the Delaunay diagrams of a set of n oints in the lane can be comuted in O(n log n) time and O(n) sace. The second Delaunay triangulation in ste 3 deals with O(n) oints as the Voronoi diagram of n oints can have at most 2n Voronoi vertices. Therefore, CRUST runs in O(n log n) time and takes O(n) sace Correctness The correctness of CRUST is roved in two arts. First, it is shown that each correct edge is resent in the outut of CRUST (Correct Edge Lemma 19). Then, it is shown that no incorrect edge is outut (Incorrect Edge Lemma 20). Lemma 19 (Correct Edge.). Each correct edge is outut by CRUST whenε< 1 5. PROOF. Let q be a correct edge. Let z be the oint where the erendicular bisector of q intersects the emty segmentγ(, q). Consider the ball B= B z, z. This ball is emty of any oint from P whenε<1 (Emty Segment Lemma 14 (i)). We show that this ball does not contain any Voronoi vertex of Vor P either. B v z B q Figure 31: Illustration for the Correct Edge Lemma 19. Suose that B contains a Voronoi vertex, say v, from V (Figure 31). Then by simle circle geometry the maximum distance of v from is 2 z. Thus, v 2 z. Since z ε f (z) by the Emty Segment Lemma 14(iii), we have v 2ε f (z) 2ε f (). The Delaunay ball B centering v contains three oints from P on its boundary. This means Bd B Σ is not a 0-shere. So, B contains a medial axis oint by the Feature Ball Lemma 11. As the Delaunay ball B is emty, cannot lie in Int B. So, the medial axis oint in B lies within 2 v distance from. Therefore, 2 v f (). But, v 2ε f () enabling us to reach a contradiction when 2ε < 1 2, i.e., whenε< 1 5. Therefore, forε< 1 5, there is a circumscribing ball of q emty of any oint from P V. So, it aears in Del (P V) and is outut by CRUST as it connects two oints from P.

7 Notes by Tamal K. Dey, OSU 53 Lemma 20 (Incorrect Edge.). No incorrect edge is outut by CRUST whenε<1/5. PROOF. We need to show that there is no ball, emty of both samle oints and Voronoi vertices, circumscribing an incorrect edge between two samle oints, say and q. For the sake of contradiction, assume that D is such a ball. Let v and v be the two oints where the erendicular bisector of q intersects the boundary of D, see Figure 32. Consider the two balls B= B v,r and B = B v,r that circumscribe q. We claim that both B and B are emty of any samle oints. Suose on the contrary, any one of them, say B, contains a samle oint. Then, one can ush D continually towards B by moving its center on the erendicular bisector of q and keeing, q on its boundary. During this motion, the deformed D would hit a samle oint s for the first time before its center reaches v. At that moment, q, and s define a ball emty of any other samle oints. The center of this ball is a Voronoi vertex in Vor P which resides inside D. This is a contradiction as D is emty of any Voronoi vertex from V. q D B v v B 2 α x 1 Figure 32: Illustration for the Incorrect Edge Lemma 20. The angle vv isπ/2 as vv is a diameter of D. The tangents to the boundary circles of B and B at are erendicular to v and v resectively. Therefore, the tangents make an angle ofπ/2. This imlies thatσcannot be tangent to both B and B at. First consider the case whereσis tangent neither to B nor to B at. Let 1 and 2 be the oints of intersection ofσwith the boundaries of B and B resectively that are consecutive to among all such intersections. Our goal will be to show that either the curve segment 1 or the curve segment 2 intersects B or B rather deely and thereby contributing a long emty segment which is rohibited by the samling condition. The curve segment between and 1 and the curve segment between and 2 do not have any samle oint other than. By the Small Segment Lemma 15 both 1 and 2 are no more than 2ε f () forε< 1 5. So by the Segment Angle Lemma 17, 1 2 π 2 arcsin ε. Without loss of generality, let the angle between 1 and the tangent to B at be larger than the angle between 2 and the tangent to B at. Then, 1 makes an angleαwith the tangent

8 54 Notes by Tamal K. Dey, OSU to B at where α 1 2 (( π 2 arcsin = π 4 arcsin ε. ε ) π ) 2 Consider the other case whereσis tangent to one of the two balls B and B at. Without loss of generality, assume that it is tangent to B at. Again the lower bound on the angleαas stated above holds. Let x be the oint where the erendicular bisector of 1 intersects the curve segment between and 1. Clearly, x is in B. Since B intersectsσat and q which are not consecutive samle oints, it cannot containγ(, q) orγ (, q) inside comletely. This means B Σ cannot be a 1-ball. So by the Feature Ball Lemma 11, B has a medial axis oint and thus its radius r is at least f (x)/2. By simle geometry, one gets that x = r sinα 1 f (x) sinα. 2 By roerty (iii) of the Emty Segment Lemma 14 x ε f (x). We reach a contradiction if ( π 2ε<sin 4 arcsin ε ). Forε< 1 5, this inequality is satisfied. Combining the Correct Edge Lemma 19 and the Incorrect Edge Lemma 20 we get the following theorem. Theorem 21. Forε< 1 5, CRUST oututs all and only correct edges. 22 NN-crust The next algorithm for curve reconstruction is based on the concet of nearest neighbors. A oint P is a nearest neighbor of q P if there is no other oint s P\{, q} with q s < q. Notice that being a nearest neighbor of q does not necessarily mean that q is a nearest neighbor of. We first observe that edges that connect nearest neighbors in P must be correct edges if P is sufficiently dense. But, all correct edges do not connect nearest neighbors. Figure 33 shows all edges that connect nearest neighbors. The missing correct edges in this examle connect oints that are not nearest neighbors. However, these correct edges connect oints that are not very far from being nearest neighbors. We cature them in NN-CRUST using the notion of half neighbors.

9 Notes by Tamal K. Dey, OSU 55 r q r q (a) (b) Figure 33: (a) Only nearest neighbor edges may not reconstruct a curve, (b) half neighbor edges such as r fill u the gas Algorithm Let q be an edge connecting to its nearest neighbor q and q be the vector from to q. Consider the closed halflane H bounded by the line assing through with q as outward normal. Clearly, q H. The nearest neighbor to in the set H Pis called its half neighbor. In Figure 33(b), r is the half neighbor of. It can be shown that two correct edges incident to a samle oint connect it to its nearest and half neighbors. The above discussion immediately suggests an algorithm for curve reconstruction. But, we need efficient algorithms to comute nearest neighbor and half neighbor for each samle oint. The Delaunay triangulation Del P turns out to be useful for this comutation as all correct edges are Delaunay if P is sufficiently dense. The Small Edge Lemma 16 imlies that, for each samle oint, it is sufficient to check only the Delaunay edges to determine correct edges. We check all edges incident to in Del P and determine the shortest edge connecting it to its nearest neighbor, say q. Next, we check all other edges incident to which make at least π 2 angle with q at and choose the shortest among them. This second edge connects to its half neighbor. The entire comutation can be done in time roortional to the number of edges incident to. Since the sum of the number of incident edges over all vertices in the Delaunay triangulation is O(n) where P =n, correct edge comutation takes only O(n) time once Del P is comuted. The Delaunay triangulation of a set of n oints in the lane can be comuted in O(n log n) time which imlies that NN-crust takes O(n log n) time. NN-CRUST(P) 1 comute Del P; 2 E= ; 3 for each Pdo 4 comute the shortest edge q in Del P; 5 comute the shortest edge s so that qs π 2 ; 6 E=E {q, s}; 7 endfor 8 outut E.

10 56 Notes by Tamal K. Dey, OSU 22.2 Correctness As we discussed before, NN-CRUST comutes edges connecting each samle oint to its nearest and half neighbors. The correctness of NN-CRUST follows from the roofs that these edges are correct. s m γ q s γ q (a) (b) Figure 34: Diametric ball of q intersectsσin (a) two comonents, (b) single comonent. Lemma 22 (Neighbor.). Let P be any samle oint and q be its nearest neighbor. The edge q is correct forε< 1 3. PROOF. Consider the ball B with q as diameter. If B does not intersectσin a 1-ball, it contains a medial axis oint by the Feature Ball Lemma 11. See Figure 34(a). This means q > f (). A correct edge s satisfies s 2ε f () by the Small Edge Lemma 16. Thus, forε< 1 3 we have s < q, a contradiction to the fact that q is the nearest neighbor to. So, B intersectsσin a 1-ball, namelyγ=γ(, q) as shown in Figure 34(b). If q is not correct,γcontains a samle oint, say s, between and q inside B. Again, we reach a contradiction as s < q. Next we show that edges connecting a samle oint to its half neighbors are also correct. Lemma 23 (Half Neighbor.). An edge q where q is a half neighbor of is correct whenε< 1 3. PROOF. Let r be the nearest neighbor of. According to the definition q makes at least π 2 angle with r. If q is not correct, consider the correct edge s incident to other than r. By the Edge Angle Lemma 18 s also makes at least π 2 angle with r forε<1/3. We show that s is closer to than q. This contradicts that q is the half neighbor of since both s and q make an angle at least π 2 with r. Consider the ball B with q as a diameter. If B does not intersectσin a 1-ball (Figure 35(a)), it would contain a medial axis oint and thus q f (). On the other hand, forε< 1 3, s 2ε f () by the Small Edge Lemma 16. We get s < q forε < 1 3 as required for contradiction. Next, assume that B intersects Σ in a 1-ball, namely in γ(, q), as in Figure 35(b). Since q is not a correct edge, s must be on this curve segment. It imlies s < q as required for contradiction.

11 Notes by Tamal K. Dey, OSU 57 s r m γ q r s γ q (a) (b) Figure 35: Diametric ball of q intersectsσin (a) more than one comonent, (b) a single comonent. Theorem 24. NN-CRUST comutes all and only correct edges whenε< 1 3. PROOF. By the Small Edge Lemma 16 all correct edges are Delaunay. Ste 4 and 5 assure that all edges joining samles oints to their nearest and half neighbors are comuted as outut. These edges are correct by the Neighbor Lemma 22 and the Half Neighbor Lemma 23 whenε< 1 3. Also, there is no other correct edges since each samle oint can only be incident to exactly two correct edges. Exercises (The exercise numbers with the suerscrit h and o indicate hard and oen questions resectively.) 1. Give an examle of a oint set P such that P is an 1-samle of two curves for which the correct reconstructions are different. 2. Given a 1 4-samle P of a smooth curve, show that all correct edges are Gabriel in Del (P V) where V is the set of Voronoi vertices in Vor P. 3. Let P be anε-samle of a smooth curve without boundary. Letη q be the sum of the angles oosite to q in the two (or one if q is a convex hull edge) triangles incident to q in Del P. Prove that there is anεfor which q is correct if and only ifη q <π. 4. Show that the NN-CRUST algorithm can reconstruct curves in three dimensions from sufficiently dense samles. 5. The Correct Edge Lemma 19 is roved forε< 1 5. Show that it also holds forε 1 5. Similarly show that the Neighbor Lemma 22 and the Half Neighbor Lemma 23 hold for ε 1/3. 6 h. Establish a relation betweenαandδto guarantee that anα-shae reconstructs a smooth curve in the lane from a globallyδ-uniform samle. 7 o. It is known that the NN-CRUST algorithm can be roved to reconstruct curves fromεsamles forε<0.5. Can this bound onεbe imroved? What is the largest value ofε for which curves can be reconstructed fromε-samles?

12 58 Notes by Tamal K. Dey, OSU 8 h. Let v V be a Voronoi vertex in the Voronoi diagram Vor P of anε-samle P of a smooth curveσ. Show that there exists a oint m in the medial axis ofσso that m v =Õ(ε) f () whenεis sufficiently small (see Section 18.3 for Õ definition). References [1] T. K. Dey. Curve and Surface Reconstruction: Algorithms with Mathematical Analysis. Cambridge U. Press, 2007.