Cross products Line segments The convex combination of two distinct points p
|
|
|
- Jared Lloyd
- 5 years ago
- Views:
Transcription
1 CHAPTER Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter aided design statistics Deals with geometric objects such as oints, line segments, olygons, etc. Some tyical roblems considered: whether intersections occur in a set of lines. finding vertices of a conve hull for oints. whether a line can be drawn searating two sets of oints. whether one oint is visible from a second oint, given some olygons that may block visibility. otimal location of fire towers to view a region. closest or most distant air of oints. whether a oint is inside or outside a olygon. Advanced Algorithms, Feodor F. Dragan, Kent State University Cross roducts Line segments The conve combination of two distinct oints = (, y) and = (, y) is any oint = (, y) such that for some real number α with 0 α,, y ) = α(, y ) + ( α)(, ). ( y, the line segment joining and, is the set of all conve combinations of and. Intuition roblem: Show that if (,y) is a conve combination of (, y) and (, y) then y y y y α = = which is the standard equation of a line with sloe α. Cross roducts let and be oints on the lane The cross roduct corresonds to the signed area in the arallelogram. = det = y y =. y y y + Advanced Algorithms, Feodor F. Dragan, Kent State University (0,0)
2 If is negative, then o is counterclockwise from o. If is ositive, then o is clockwise from o. If 0, then o and o are collinear. = Cross roducts (cont.) y To determine if is clockwise from 0 0, we translate 0 to the origin and consider ' ' where ' = 0, ' = 0. ' ' = ( 0)( y y0) ( 0)( y y0). o Prohibited for If o is clockwise from (0,0) o Consider now whether two consecutive line segments and turn left or right at. 0 Check whether 0 is clockwise from 0 ( 0) ( 0) < 0 So, counterclockwise or left turn ( 0) ( 0) > 0 So, clockwise or right turn 0 0 Advanced Algorithms, Feodor F. Dragan, Kent State University Intersection of two line segments A two stage rocess is used. The first stage is called quick-rejection. Bounding Bo: The bounding bo of a geometric figure is the smallest rectangle that contains the figure and whose segments are arallel to and y ais. The bounding bo ( ˆ, ˆ ) of the line segment is the bo with lower lefthand oint ˆ ( ˆ, ˆ ), where = y ˆ = min(, ) yˆ = min( y, y ) and with uer right-hand oint ˆ = ( ˆ, yˆ ), where ˆ = ma(, ) yˆ = ma( y, y ) Intersection of bounding boes: Rectangles ( ˆ, ˆ ) and ( ˆ, ˆ 4) intersect if and only if the following is true: ( ˆ, ˆ 4) ˆ ˆ ) Λ( ˆ ˆ ) Λ( yˆ yˆ ) Λ( yˆ ˆ ) ( 4 4 y ŷ 4 this will not ass the quick rejection test ŷ ŷ ŷ ˆ, ˆ ) ( (0,0) ˆ ˆ ˆ 4 ˆ Advanced Algorithms, Feodor F. Dragan, Kent State University 4
3 Intersection of two line segments (cont.) Second stage: Decide whether each segment meets ( straddles ) the line containing the other. A segment straddles a line if lies on one side of the line and on the other side. (the segment straddles the line also if or lies on the line) Observation: Two segments intersect iff they ass the quick rejection test and each segment straddles the other. Testing straddle with cross roducts: we show how to check if straddles the line L determined by and If 4 does straddle the line containing and, then the following have different signs. ( ) ( ) ( ) ( ) Boundary cases where 4 straddles L At least one cross roduct is zero. Both cases ass the quick rejection test. 4 4 Advanced Algorithms, Feodor F. Dragan, Kent State University 5 Determining whether any air of segments intersect. Given n line segments, determine whether any air of them intersect. Sweeing: An imaginary vertical swee line moves across the -ais (which acts as a time ais) from left to right. All line segment endoints are considered in a left-to-right order. Whenever endoint is found, a check for an intersection is made. Algorithm runs in O(n logn) time, where n is the number of segments. Algorithm does not look for all intersections, but just whether or not there is at least one intersection. It takes Ω( n ) time in the worst case to find all intersections (see Eercise.-) Standard simlifying assumtions: no inut segment is vertical no three inut segments intersect at a single oint. Order definition: Let s and s be two segments s These segments are comarable at t if the vertical swee line with -coordinate t intersects both segments. s If s and s are comarable at t, then s is above s, written s > t s, if s intersects the swee line at t at a higher oint than s. t Advanced Algorithms, Feodor F. Dragan, Kent State University 6
4 > is a total order for each value of (refleive, antisymmetric, transitive) order > changes as changes (swee line status and event oint schedule). a segment obtains an order when its left endoint is encountered by swee line. a segment looses its order when swee line reaches its right endoint. swee line behavior near an intersection oint if the intersection oint is not on a swee line, then there eist lines v and w immediately to the right and left of the intersection. the segment that has the higher intersection at v reverses its order with other segment as swee line asses from v to w. if is the leftmost intersection oint and is at intersection of segments a and b, then a and b intersect v at adjacent oints a and b are called consecutive at v. Advanced Algorithms, Feodor F. Dragan, Kent State University 7 v a b w The Algorithm ANY-SEGMENTS-INTERSECTION(S) To maintain a total ordering T on the swee line as it moves, we need the following oerations: INSERT(T,s) insert segment s into T DELETE(T,s) delete segment s from T ABOVE(T,s) return the segment from T immediately above segment s BELOW(T,s) return the segment from T immediately below segment s Red-black trees can rovide a balanced search tree which can suort above oerations in O(log n) time (see Ch. in CLRS) () T emtyset () Sort segment endoints from left to right. Break ties by utting oint with lower y-coordinate first. () For each oint in the sorted list (in order) (4) if is left endoint of segment s then (5) INSERT(T,s) (6) if [ABOVE(T,s) eists and it intersects s] or [BELOW(T,s) eists and it intersects s] then return TRUE (7) if is the right endoint of segment then (8) if both [ABOVE(T,s) and BELOW(T,s) eist] and [ABOVE(T,s) intersects BELOW(T,s)] then return TRUE (9) DELETE(T,s) Animated demo (0) return FALSE htt:// Advanced Algorithms, Feodor F. Dragan, Kent State University 8 4
5 Comments and Correctness Sorting on line () will sort oints leicograhically and require O(n logn) time. A boundary case occurs if oint in algorithm also lies on another segment s. In this case s and s should be in consecutive order at. Correctness Theorem: A call to ANY-SEGMENTS-INTERSECTION(S) returns true iff there is an intersection among the segments of S. If a true is returned, an intersection has been found between the two segments. Suose a false is returned, but an intersection actually eists. Let be the leftmost intersection oint (break ties by taking lowest y-coordinate). Let a and b be segments intersecting at. Since no intersection occurs to left of, T gives the correct order rior to. that is, no reversals in order have occurred. Since no three segments intersect at the same oint, there eists a swee line z at which a and b become consecutive. z is to the left of or goes through. There is an endoint q on z that is the event at which a and b become consecutive. If is on swee line z, then =q. If not, then q is left of. Advanced Algorithms, Feodor F. Dragan, Kent State University 9 c z q a b Correctness and Runtime In either case, the order of T is correct before q is rocessed. Only two cases are ossible.. Either a or b is inserted into T at z and the other segment is above or below it. (In this case, intersection is detected by line (6).). Segments a and b are already in T and a segment c between them is deleted at z. (In this case, an intersection is detected by line (8).) In either case the intersection of a and b at is detected, so rocedure cannot return a FALSE, as suosed. c q a b Running Time: sort on line () takes O(n logn) time, using merge or hea sort. since there are n events (endoints) where swee line stos, the loo iterates at most n times. each iteration of loo takes O(log n) time, since red-black tree oerations take O(log n) time. Total time is O(n logn). READ Ch.. and Ch. in CLRS. Advanced Algorithms, Feodor F. Dragan, Kent State University 0 z 5
6 Conve Hull Algorithms Definitions and Proerties: Given n oints on the lane Q = { n,,..., }. Intersection of all conve sets containing Q Smallest conve set containing Q Intersection of all half-lanes containing Q Union of all triangles formed by oints of Q Smallest conve olygon containing Q All vertices of hull are some oints of Q rubber band etreme oint always unique not etreme oint NOTE: conve-hull(q) is the closed solid region, not just the boundary CH(Q) Advanced Algorithms, Feodor F. Dragan, Kent State University The Problem and Aroaches Problem: Given n oints on the lane Q = {,,..., Aroaches: Brute Force Gift Wraing QuickHull Graham Scan Incremental Divide and Conquer By Delaunay Triangulation & Voronoi Diagram n }, find CH(Q). Brute-Force Aroach Determine etreme edges: q for each air of oints,q Q do if all other oints lie on one side of line assing thru and q then kee edge (, q) Sort edges in counterclockwise order (we want outut in counterclockwise) Running time: O(n ) bad but not the worst yet Advanced Algorithms, Feodor F. Dragan, Kent State University 6
7 Gift Wraing or The Jarvis March Algorithm First suggested by Chand and Kaur (970). Then by Jarvis (97). Worst-case time: O(n ) Outut-sensitive time: O(nh), where h is the # of vertices of hull Can be etended to higher dimension was the rimary algorithm for higher dimensions for quite some time Method: Let 0 be the lowest oint (take leftmost oint in case of tie) The net conve hull verte has the least olar angle w.r.t. the ositive horizontal ray from 0. Measure in counterclockwise If tie, choose the furthest such oint Vertices,,, k are icked similarly where k is the highest oint (leftmost) The sequence 0,,,,, k is the right chain of CH(Q). To choose the left chain of CH(Q), start with k choose k+ as the oint with least angle w.r.t. the negative horizontal ray from k k again, measure in counterclockwise direction and if tie occurs, choose furthest such oint. continue in same fashion until you obtain k, k+,, t = 0 0 Advanced Algorithms, Feodor F. Dragan, Kent State University Comleity of Jarvis March For each verte from CH(Q), it takes O() time to comare the olar angle of q j and qi using cross-roduct O(n) time to find minimum olar angle O(n) total time If CH(Q) has h vertices, then the running time is O(nh). In worst case h=o(n), hence O( n ) is worst case time bound. Worst case occurs when O(n) of oints lie on the conve hull, e.g., all oints lie on a circle. If oints in Q are generated by random generator, then we eect h= O(logn) In ractice, Jarvis march is normally very fast. If h=o(log n), then this algorithm is asymtotically fastest. Theorem: Ω( n log n) is a lower bound for comuting the conve hull. Assume we want to sort n numbers,,..., } { n create n oints on lane i = ( i, yi) where yi = i ( i =,..., n). y construct CH = CH ({,,..., n}) get from descrition of CH original numbers in sorted order Conclusion: If we can construct CH in o(n logn) time then we can sort n numbers in o(n logn) time, which is imossible. Advanced Algorithms, Feodor F. Dragan, Kent State University 4 (0,0) 7
8 Graham Scan Algorithm First a base oint 0 is selected. Normally this is the oint with minimum y- coordinate (select leftmost in case of tie) Net all oints are sorted w.r.t. the olar angle they make with a half-ray with left endoint 0 and arallel to -ais. (!!! We do not need to comute those angles!!!) 4 remove Interior oints on ray cannot be conve hull oints and are removed during sort Remaining oints are stored in counterclockwise order w.r.t. 0 Let 0,,,,, m ( m n) be the sorted list of remaining oints. Clearly, 0 and are in CH(Q). Let S be a stack in which oints that are otentially conve hull oints will be stored. Initially S = 0. Remaining stes of the algorithm follow for i to m do while (the angle formed by oints NEXT_TO_TOP(S), TOP(S), and i make a non-left turn) POP(S) PUSH(S, i ) return S Advanced Algorithms, Feodor F. Dragan, Kent State University Eamle and Runtime Comutation Note straight line here. 4 is eliminated, as non-left turn. 8 CH(Q)={ 0,,, 5, 7, 8 } Requires O(n) to find 0 Sorting based on olar angle takes O(n logn) time Removal of n-m oints with dulicate angles takes O(n). For loo is eecuted m- times, hence O(n). Interior while statement is a roblem. It may iterate as many as O(n) time. Above observation can easily lead to an over-estimate of O( n ). Note that each ass through while statement, POP is eecuted. As in analysis of MULTIPOP, there is at most one POP oeration for each PUSH oeration (see amortized analysis) Since 0,, m are not oed, at most m- POP oerations occur. Note, both POP and test for while take O() time and m n. Hence amortized cost for each iteration of while loo is O(). Overall worst-case cost of for-loo is O(n) Worst-case running time of the algorithm is O(n logn) (= O(n logn) + O(n)). Advanced Algorithms, Feodor F. Dragan, Kent State University 6 8
9 Correctness of Graham Scan Claim : Each oint oed from stack S is not a verte of CH(Q) and lies inside new CH(S). Suose j is oed from S because k j i makes a non-left turn. Since oints are ordered in increasing olar angle w.r.t 0, the oints k j lie in counterclockwise order w.r.t. i i 0 and k j i contains j Then j cannot be a verte of CH(Q). Claim : The oints on stack S always form the vertices of a conve olygon. 0 The claim holds initially for oints 0,,. They form a triangle. The stack changes by oints being oed or ushed. If a oint is oed, then a verte is removed from conve olygon, leaving the resulting olygon conve. If a oint i is ushed, the resulting oints of S form a conve olygon. by choice of 0,, i lies above 0 (see diagram on net slide).. since a left turn occurs at j, i lies below j k. since i occurs later in the sequence than j, the olar angle of 0 i. is greater than the olar angle of 0 j. thus, i lies to the left of line 0 j,, i.e., i lies in the shaded region in diagram. so, after i is ushed on the stack, a conve region results. Advanced Algorithms, Feodor F. Dragan, Kent State University 7 j k Correctness of Graham Scan (cont.) j Diagram i k Claim : At the conclusion of the algorithm, the oints of S joined together consequently form a conve olygon that contains Q. By claim, all oints droed from S are not vertices of CH(Q). By claim, the oints of S are oints from Q that form a conve olygon By construction and claim, all oints of Q are either in S or lie interior to CH(S ) for some earlier S with CH(S ) CH(S). Then, at conclusion the oints of S joined together consequently give a conve olygon that contains all oints of Q. Animated demos htt:// htt:// htt:// htt:// Advanced Algorithms, Feodor F. Dragan, Kent State University 8 0 9
10 Closest Pair of Points Given n oints on the lane, find closest air of oints. The Euclidean distance between two oints =, ) and =, ) is ( y ( y d(, ) = ( ) + ( y y) An obvious but naïve aroach is to comute the distance between any two oints and take minimum. However, running time is n = O ( n ). A high-level descrition of a much better algorithm (at least for large sets) is given below. Let Q be a set of n lanar oints. If Q <4, then the distances between all airs of oints are comuted and the closest air is reorted. If Q >, then a Divide & Conquer & Combine rocedure is followed. Each recursive call receives as inut a set P Q arrays X and Y containing oints P sorted by and y coordinates, resectively Advanced Algorithms, Feodor F. Dragan, Kent State University 9 Divide and Conquer Stes Divide ste Find a vertical line L that bisects the oints in P into P and P with almost equal sizes. All oints in P are left of L or on L, all oints in P are right of L or on L. The array X is divided into arrays X and X which contain the oints of P and P, resectively, sorted by -coordinates. Likewise the array Y is slit into arrays Y and Y which contain the oints of P and P, resectively, sorted by y-coordinates. At the beginning, Q has to be resorted by -coordinates to obtain X and by y- coordinates to obtain Y. This we do before the first recursive call. Now, on each recursive call, the set P can easily be slit in linear time, giving sets P, P, X, and X. Both Y and Y can be formed by Y in linear time by walking through Y and utting each element in Y (or Y ) if it is in P (resectively, P ). Conquer Ste Make two recursive calls to find closest air of oints in P and P, resectively. First call gets inut (P, X, Y ) Second call gets inut (P,X,Y ) Set closest air returned for P and P have distance d and d, resectively. Set d = min{d, d } Advanced Algorithms, Feodor F. Dragan, Kent State University 0 0
11 Combine Combine Ste and Runtime Observe that if there is a air in P closer than d, then they must lie in a d d bo about L, as follows. There can be at most 8 oints in each stri. Find the array Y consisting of the oints of Y within d of L, sorted by their y- coordinate. d d If d<d, then the closest air with distance d is returned. Otherwise, the closest air formed by the two recursive calls is returned. Runtime The initial rerocessing ste costs O(n logn) The recurrence relation for the recursive ortion is T(n), T ( n / ) + O( n) if n > where T ( n) = O() if n Its solution is T(n)= O(n logn). This gives also the total running time. Advanced Algorithms, Feodor F. Dragan, Kent State University d d L d d L Possible coincident oints, one in P and one in P. Net, for each oint from Y, check to see if d(,q)<d for each of the 7 oints q that follow in Y. Find the closest-air distance d, comuted in receding ste over all oints in Y. READ Ch.. and.4 in CLRS. Homework 4: Problems: 0.5- (in CLR only),.- (. 99) (= roblem 5.- in CLR),.-4 (. 946) (= roblem 5.-4 in CLR),.-4 ( ) (= roblem 5.-4 in CLR),.4- (. 96) (= roblem 5.4- in CLR), Etra credit roblem:.-8 (. 940) (= roblem 5.-7 in CLR) Advanced Algorithms, Feodor F. Dragan, Kent State University
Cross products. p 2 p. p p1 p2. p 1. Line segments The convex combination of two distinct points p1 ( x1, such that for some real number with 0 1,
 CHAPTER 33 Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
CHAPTER 33 Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
Graduate Algorithms CS F-19 Computational Geometry
 Graduate Algorithms CS673-016F-19 Comutational Geometry David Galles Deartment of Comuter Science University of San Francisco 19-0: Cross Products Given any two oints 1 = (x 1,y 1 ) and = (x,y ) Cross
Graduate Algorithms CS673-016F-19 Comutational Geometry David Galles Deartment of Comuter Science University of San Francisco 19-0: Cross Products Given any two oints 1 = (x 1,y 1 ) and = (x,y ) Cross
COT5405: GEOMETRIC ALGORITHMS
 COT5405: GEOMETRIC ALGORITHMS Objects: Points in, Segments, Lines, Circles, Triangles Polygons, Polyhedra R n Alications Vision, Grahics, Visualizations, Databases, Data mining, Networks, GIS Scientific
COT5405: GEOMETRIC ALGORITHMS Objects: Points in, Segments, Lines, Circles, Triangles Polygons, Polyhedra R n Alications Vision, Grahics, Visualizations, Databases, Data mining, Networks, GIS Scientific
Convex Hulls. Helen Cameron. Helen Cameron Convex Hulls 1/101
 Convex Hulls Helen Cameron Helen Cameron Convex Hulls 1/101 What Is a Convex Hull? Starting Point: Points in 2D y x Helen Cameron Convex Hulls 3/101 Convex Hull: Informally Imagine that the x, y-lane is
Convex Hulls Helen Cameron Helen Cameron Convex Hulls 1/101 What Is a Convex Hull? Starting Point: Points in 2D y x Helen Cameron Convex Hulls 3/101 Convex Hull: Informally Imagine that the x, y-lane is
Lecture 3: Geometric Algorithms(Convex sets, Divide & Conquer Algo.)
 Advanced Algorithms Fall 2015 Lecture 3: Geometric Algorithms(Convex sets, Divide & Conuer Algo.) Faculty: K.R. Chowdhary : Professor of CS Disclaimer: These notes have not been subjected to the usual
Advanced Algorithms Fall 2015 Lecture 3: Geometric Algorithms(Convex sets, Divide & Conuer Algo.) Faculty: K.R. Chowdhary : Professor of CS Disclaimer: These notes have not been subjected to the usual
Lecture 2: Fixed-Radius Near Neighbors and Geometric Basics
 structure arises in many alications of geometry. The dual structure, called a Delaunay triangulation also has many interesting roerties. Figure 3: Voronoi diagram and Delaunay triangulation. Search: Geometric
structure arises in many alications of geometry. The dual structure, called a Delaunay triangulation also has many interesting roerties. Figure 3: Voronoi diagram and Delaunay triangulation. Search: Geometric
Lecture 8: Orthogonal Range Searching
 CPS234 Comutational Geometry Setember 22nd, 2005 Lecture 8: Orthogonal Range Searching Lecturer: Pankaj K. Agarwal Scribe: Mason F. Matthews 8.1 Range Searching The general roblem of range searching is
CPS234 Comutational Geometry Setember 22nd, 2005 Lecture 8: Orthogonal Range Searching Lecturer: Pankaj K. Agarwal Scribe: Mason F. Matthews 8.1 Range Searching The general roblem of range searching is
Computational Geometry Overview from Cormen, et al.
 UMass Lowell Computer Science 91.503 Graduate Algorithms Prof. Karen Daniels Spring, 2014 Computational Geometry Overview from Cormen, et al. Chapter 33 (with additional material from other sources) 1
UMass Lowell Computer Science 91.503 Graduate Algorithms Prof. Karen Daniels Spring, 2014 Computational Geometry Overview from Cormen, et al. Chapter 33 (with additional material from other sources) 1
The Spatial Skyline Queries
 Coffee sho The Satial Skyline Queries Mehdi Sharifzadeh and Cyrus Shahabi VLDB 006 Presented by Ali Khodaei Coffee sho Three friends Coffee sho Three friends Don t choose this lace is closer to each three
Coffee sho The Satial Skyline Queries Mehdi Sharifzadeh and Cyrus Shahabi VLDB 006 Presented by Ali Khodaei Coffee sho Three friends Coffee sho Three friends Don t choose this lace is closer to each three
Computational geometry
 Computational geometry Inge Li Gørtz CLRS Chapter 33.0, 33.1, 33.3. Computational Geometry Geometric problems (this course Euclidean plane). Does a set of line segments intersect, dividing plane into regions,
Computational geometry Inge Li Gørtz CLRS Chapter 33.0, 33.1, 33.3. Computational Geometry Geometric problems (this course Euclidean plane). Does a set of line segments intersect, dividing plane into regions,
CMSC 754 Computational Geometry 1
 CMSC 754 Comutational Geometry 1 David M. Mount Deartment of Comuter Science University of Maryland Fall 2002 1 Coyright, David M. Mount, 2002, Det. of Comuter Science, University of Maryland, College
CMSC 754 Comutational Geometry 1 David M. Mount Deartment of Comuter Science University of Maryland Fall 2002 1 Coyright, David M. Mount, 2002, Det. of Comuter Science, University of Maryland, College
CSE 5311 Notes 13: Computational Geometry
 CSE 5311 Notes 13: Computational Geometry (Last updated 4/17/17 4:39 PM) SMALLEST ENCLOSING DISK See section 4.7 of de Berg ( http://dx.doi.org.ezproxy.uta.edu/10.1007/978-3-540-77974-2 ) Algorithm MINIDISC(P)
CSE 5311 Notes 13: Computational Geometry (Last updated 4/17/17 4:39 PM) SMALLEST ENCLOSING DISK See section 4.7 of de Berg ( http://dx.doi.org.ezproxy.uta.edu/10.1007/978-3-540-77974-2 ) Algorithm MINIDISC(P)
We will then introduce the DT, discuss some of its fundamental properties and show how to compute a DT directly from a given set of points.
 Voronoi Diagram and Delaunay Triangulation 1 Introduction The Voronoi Diagram (VD, for short) is a ubiquitious structure that aears in a variety of discilines - biology, geograhy, ecology, crystallograhy,
Voronoi Diagram and Delaunay Triangulation 1 Introduction The Voronoi Diagram (VD, for short) is a ubiquitious structure that aears in a variety of discilines - biology, geograhy, ecology, crystallograhy,
Computing the Convex Hull of. W. Hochstattler, S. Kromberg, C. Moll
 Reort No. 94.60 A new Linear Time Algorithm for Comuting the Convex Hull of a Simle Polygon in the Plane by W. Hochstattler, S. Kromberg, C. Moll 994 W. Hochstattler, S. Kromberg, C. Moll Universitat zu
Reort No. 94.60 A new Linear Time Algorithm for Comuting the Convex Hull of a Simle Polygon in the Plane by W. Hochstattler, S. Kromberg, C. Moll 994 W. Hochstattler, S. Kromberg, C. Moll Universitat zu
Computational Geometry. Algorithm Design (10) Computational Geometry. Convex Hull. Areas in Computational Geometry
 Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
Convex Hull Algorithms
 Convex Hull Algorithms Design and Analysis of Algorithms prof. F. Malucelli Villa Andrea e Ceriani Simone Outline Problem Definition Basic Concepts Bruteforce Algorithm Graham Scan Algorithm Divide and
Convex Hull Algorithms Design and Analysis of Algorithms prof. F. Malucelli Villa Andrea e Ceriani Simone Outline Problem Definition Basic Concepts Bruteforce Algorithm Graham Scan Algorithm Divide and
CMSC 425: Lecture 16 Motion Planning: Basic Concepts
 : Lecture 16 Motion lanning: Basic Concets eading: Today s material comes from various sources, including AI Game rogramming Wisdom 2 by S. abin and lanning Algorithms by S. M. LaValle (Chats. 4 and 5).
: Lecture 16 Motion lanning: Basic Concets eading: Today s material comes from various sources, including AI Game rogramming Wisdom 2 by S. abin and lanning Algorithms by S. M. LaValle (Chats. 4 and 5).
Range Searching. Data structure for a set of objects (points, rectangles, polygons) for efficient range queries.
 Range Searching Data structure for a set of objects (oints, rectangles, olygons) for efficient range queries. Y Q Deends on tye of objects and queries. Consider basic data structures with broad alicability.
Range Searching Data structure for a set of objects (oints, rectangles, olygons) for efficient range queries. Y Q Deends on tye of objects and queries. Consider basic data structures with broad alicability.
Shuigeng Zhou. May 18, 2016 School of Computer Science Fudan University
 Query Processing Shuigeng Zhou May 18, 2016 School of Comuter Science Fudan University Overview Outline Measures of Query Cost Selection Oeration Sorting Join Oeration Other Oerations Evaluation of Exressions
Query Processing Shuigeng Zhou May 18, 2016 School of Comuter Science Fudan University Overview Outline Measures of Query Cost Selection Oeration Sorting Join Oeration Other Oerations Evaluation of Exressions
CS 532: 3D Computer Vision 14 th Set of Notes
 1 CS 532: 3D Computer Vision 14 th Set of Notes Instructor: Philippos Mordohai Webpage: www.cs.stevens.edu/~mordohai E-mail: Philippos.Mordohai@stevens.edu Office: Lieb 215 Lecture Outline Triangulating
1 CS 532: 3D Computer Vision 14 th Set of Notes Instructor: Philippos Mordohai Webpage: www.cs.stevens.edu/~mordohai E-mail: Philippos.Mordohai@stevens.edu Office: Lieb 215 Lecture Outline Triangulating
Advanced Algorithm Homework 4 Results and Solutions
 Advanced Algorithm Homework 4 Results and Solutions ID 1 2 3 4 5 Av Ex 2554 6288 9919 10 6 10 10 9.5 8.9 10-1 4208 10 10 9 8.5 10 9.5 9 0996 10 10 10 10 10 10 10 8239 10 10 10 10 10 10 10 7388 8 8.5 9
Advanced Algorithm Homework 4 Results and Solutions ID 1 2 3 4 5 Av Ex 2554 6288 9919 10 6 10 10 9.5 8.9 10-1 4208 10 10 9 8.5 10 9.5 9 0996 10 10 10 10 10 10 10 8239 10 10 10 10 10 10 10 7388 8 8.5 9
Geometric Algorithms. 1. Objects
 Geometric Algorithms 1. Definitions 2. Line-Segment properties 3. Inner Points of polygons 4. Simple polygons 5. Convex hulls 6. Closest pair of points 7. Diameter of a point set 1. Objects 2-dimensional
Geometric Algorithms 1. Definitions 2. Line-Segment properties 3. Inner Points of polygons 4. Simple polygons 5. Convex hulls 6. Closest pair of points 7. Diameter of a point set 1. Objects 2-dimensional
Computational Geometry. Geometry Cross Product Convex Hull Problem Sweep Line Algorithm
 GEOMETRY COMP 321 McGill University These slides are mainly compiled from the following resources. - Professor Jaehyun Park slides CS 97SI - Top-coder tutorials. - Programming Challenges books. Computational
GEOMETRY COMP 321 McGill University These slides are mainly compiled from the following resources. - Professor Jaehyun Park slides CS 97SI - Top-coder tutorials. - Programming Challenges books. Computational
CS 410/584, Algorithm Design & Analysis, Lecture Notes 8
 CS 410/584,, Computational Geometry Algorithms for manipulation of geometric objects We will concentrate on 2-D geometry Numerically robust try to avoid division Round-off error Divide-by-0 checks Techniques
CS 410/584,, Computational Geometry Algorithms for manipulation of geometric objects We will concentrate on 2-D geometry Numerically robust try to avoid division Round-off error Divide-by-0 checks Techniques
Last time. Today: Convex Hull Brute Force Inside(q,abc) Intersect(ab,cd) Orient(a,b,c).
 Last time Convex Hull Brute Force Inside(q,abc) Intersect(ab,cd) Orient(a,b,c). Today: More efficient convex hull algorithms and absolute bounds. Two (of many) algorithms. One (of one) interesting reduction.
Last time Convex Hull Brute Force Inside(q,abc) Intersect(ab,cd) Orient(a,b,c). Today: More efficient convex hull algorithms and absolute bounds. Two (of many) algorithms. One (of one) interesting reduction.
Advanced Algorithms Computational Geometry Prof. Karen Daniels. Spring, 2010
 UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Spring, 2010 Lecture 3 O Rourke Chapter 3: 2D Convex Hulls Thursday, 2/18/10 Chapter 3 2D Convex Hulls
UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Spring, 2010 Lecture 3 O Rourke Chapter 3: 2D Convex Hulls Thursday, 2/18/10 Chapter 3 2D Convex Hulls
Computational Geometry 2D Convex Hulls. Joseph S. B. Mitchell Stony Brook University
 Computational Geometry 2D Convex Hulls Joseph S. B. Mitchell Stony Brook University Comparing O(n), O(n log n), O(n 2 ) n n log n n² 2 10 10³ 10 2 10 10 4 2 20 10 6 2 20 10 6 20 2 20 2 10 7 2 40 10 12
Computational Geometry 2D Convex Hulls Joseph S. B. Mitchell Stony Brook University Comparing O(n), O(n log n), O(n 2 ) n n log n n² 2 10 10³ 10 2 10 10 4 2 20 10 6 2 20 10 6 20 2 20 2 10 7 2 40 10 12
Voronoi Diagram and Convex Hull
 Voronoi Diagram and Convex Hull The basic concept of Voronoi Diagram and Convex Hull along with their properties and applications are briefly explained in this chapter. A few common algorithms for generating
Voronoi Diagram and Convex Hull The basic concept of Voronoi Diagram and Convex Hull along with their properties and applications are briefly explained in this chapter. A few common algorithms for generating
An improved algorithm for Hausdorff Voronoi diagram for non-crossing sets
 An imroved algorithm for Hausdorff Voronoi diagram for non-crossing sets Frank Dehne, Anil Maheshwari and Ryan Taylor May 26, 2006 Abstract We resent an imroved algorithm for building a Hausdorff Voronoi
An imroved algorithm for Hausdorff Voronoi diagram for non-crossing sets Frank Dehne, Anil Maheshwari and Ryan Taylor May 26, 2006 Abstract We resent an imroved algorithm for building a Hausdorff Voronoi
Prof. Gill Barequet. Center for Graphics and Geometric Computing, Technion. Dept. of Computer Science The Technion Haifa, Israel
 Computational Geometry (CS 236719) http://www.cs.tufts.edu/~barequet/teaching/cg Chapter 1 Introduction 1 Copyright 2002-2009 2009 Prof. Gill Barequet Center for Graphics and Geometric Computing Dept.
Computational Geometry (CS 236719) http://www.cs.tufts.edu/~barequet/teaching/cg Chapter 1 Introduction 1 Copyright 2002-2009 2009 Prof. Gill Barequet Center for Graphics and Geometric Computing Dept.
CS 410/584, Algorithm Design & Analysis, Lecture Notes 8!
 CS 410/584, Algorithm Design & Analysis, Computational Geometry! Algorithms for manipulation of geometric objects We will concentrate on 2-D geometry Numerically robust try to avoid division Round-off
CS 410/584, Algorithm Design & Analysis, Computational Geometry! Algorithms for manipulation of geometric objects We will concentrate on 2-D geometry Numerically robust try to avoid division Round-off
Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College
![Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College](/thumbs/86/93358306.jpg) Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull Given a set P of points in 2D, their convex hull is the smallest convex polygon that contains all points
Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull Given a set P of points in 2D, their convex hull is the smallest convex polygon that contains all points
Triangulation and Convex Hull. 8th November 2018
 Triangulation and Convex Hull 8th November 2018 Agenda 1. Triangulation. No book, the slides are the curriculum 2. Finding the convex hull. Textbook, 8.6.2 2 Triangulation and terrain models Here we have
Triangulation and Convex Hull 8th November 2018 Agenda 1. Triangulation. No book, the slides are the curriculum 2. Finding the convex hull. Textbook, 8.6.2 2 Triangulation and terrain models Here we have
search(i): Returns an element in the data structure associated with key i
 CS161 Lecture 7 inary Search Trees Scribes: Ilan Goodman, Vishnu Sundaresan (2015), Date: October 17, 2017 Virginia Williams (2016), and Wilbur Yang (2016), G. Valiant Adated From Virginia Williams lecture
CS161 Lecture 7 inary Search Trees Scribes: Ilan Goodman, Vishnu Sundaresan (2015), Date: October 17, 2017 Virginia Williams (2016), and Wilbur Yang (2016), G. Valiant Adated From Virginia Williams lecture
Lecture 3: Art Gallery Problems and Polygon Triangulation
 EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
Computational Geometry 2D Convex Hulls
 Computational Geometry 2D Convex Hulls Joseph S. B. Mitchell Stony Brook University Chapter 2: Devadoss-O Rourke Convexity p p Set X is convex if p,q X pq X q q convex non-convex Point p X is an extreme
Computational Geometry 2D Convex Hulls Joseph S. B. Mitchell Stony Brook University Chapter 2: Devadoss-O Rourke Convexity p p Set X is convex if p,q X pq X q q convex non-convex Point p X is an extreme
521493S Computer Graphics Exercise 3 (Chapters 6-8)
 521493S Comuter Grahics Exercise 3 (Chaters 6-8) 1 Most grahics systems and APIs use the simle lighting and reflection models that we introduced for olygon rendering Describe the ways in which each of
521493S Comuter Grahics Exercise 3 (Chaters 6-8) 1 Most grahics systems and APIs use the simle lighting and reflection models that we introduced for olygon rendering Describe the ways in which each of
The Edge-flipping Distance of Triangulations
 The Edge-fliing Distance of Triangulations Sabine Hanke (Institut für Informatik, Universität Freiburg, Germany hanke@informatik.uni-freiburg.de) Thomas Ottmann (Institut für Informatik, Universität Freiburg,
The Edge-fliing Distance of Triangulations Sabine Hanke (Institut für Informatik, Universität Freiburg, Germany hanke@informatik.uni-freiburg.de) Thomas Ottmann (Institut für Informatik, Universität Freiburg,
level 0 level 1 level 2 level 3
 Communication-Ecient Deterministic Parallel Algorithms for Planar Point Location and 2d Voronoi Diagram? Mohamadou Diallo 1, Afonso Ferreira 2 and Andrew Rau-Chalin 3 1 LIMOS, IFMA, Camus des C zeaux,
Communication-Ecient Deterministic Parallel Algorithms for Planar Point Location and 2d Voronoi Diagram? Mohamadou Diallo 1, Afonso Ferreira 2 and Andrew Rau-Chalin 3 1 LIMOS, IFMA, Camus des C zeaux,
Constrained Empty-Rectangle Delaunay Graphs
 CCCG 2015, Kingston, Ontario, August 10 12, 2015 Constrained Emty-Rectangle Delaunay Grahs Prosenjit Bose Jean-Lou De Carufel André van Renssen Abstract Given an arbitrary convex shae C, a set P of oints
CCCG 2015, Kingston, Ontario, August 10 12, 2015 Constrained Emty-Rectangle Delaunay Grahs Prosenjit Bose Jean-Lou De Carufel André van Renssen Abstract Given an arbitrary convex shae C, a set P of oints
1/60. Geometric Algorithms. Lecture 1: Introduction. Convex Hulls
 1/60 Geometric Algorithms Lecture 1: Introduction Convex Hulls Geometric algorithms scope 2/60 Geometry algorithms (practice): Study of geometric problems that arise in various applications and how algorithms
1/60 Geometric Algorithms Lecture 1: Introduction Convex Hulls Geometric algorithms scope 2/60 Geometry algorithms (practice): Study of geometric problems that arise in various applications and how algorithms
Computational Geometry
 Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
arxiv: v1 [math.gt] 1 May 2018
![arxiv: v1 [math.gt] 1 May 2018 arxiv: v1 [math.gt] 1 May 2018](/thumbs/94/118297333.jpg) CIRCUIT PRESENTATION AND LATTICE STICK NUMBER WITH EXACTLY 4 z-sticks HYOUNGJUN KIM AND SUNGJONG NO arxiv:805.0023v [math.gt] May 208 Abstract. The lattice stick number s L(L) of a link L is defined to
CIRCUIT PRESENTATION AND LATTICE STICK NUMBER WITH EXACTLY 4 z-sticks HYOUNGJUN KIM AND SUNGJONG NO arxiv:805.0023v [math.gt] May 208 Abstract. The lattice stick number s L(L) of a link L is defined to
Computational Geometry
 Motivation Motivation Polygons and visibility Visibility in polygons Triangulation Proof of the Art gallery theorem Two points in a simple polygon can see each other if their connecting line segment is
Motivation Motivation Polygons and visibility Visibility in polygons Triangulation Proof of the Art gallery theorem Two points in a simple polygon can see each other if their connecting line segment is
UPDATING ALGORITHMS FOR CONSTRAINT DELAUNAY TIN
 UPDATING ALGORITMS FOR CONSTRAINT DELAUNAY TIN WU LiXin a,b WANG YanBing a, c a Institute for GIS/RS/GPS & Subsidence Engineering Research, China Uni Mining & Technology, Beijing, China, 100083 - awulixin@263.net,
UPDATING ALGORITMS FOR CONSTRAINT DELAUNAY TIN WU LiXin a,b WANG YanBing a, c a Institute for GIS/RS/GPS & Subsidence Engineering Research, China Uni Mining & Technology, Beijing, China, 100083 - awulixin@263.net,
Design and Analysis of Algorithms Prof. Madhavan Mukund Chennai Mathematical Institute
 Design and Analysis of Algorithms Prof. Madhavan Mukund Chennai Mathematical Institute Module 07 Lecture - 38 Divide and Conquer: Closest Pair of Points We now look at another divide and conquer algorithm,
Design and Analysis of Algorithms Prof. Madhavan Mukund Chennai Mathematical Institute Module 07 Lecture - 38 Divide and Conquer: Closest Pair of Points We now look at another divide and conquer algorithm,
CS335 Fall 2007 Graphics and Multimedia. 2D Drawings: Lines
 CS335 Fall 007 Grahics and Multimedia D Drawings: Lines Primitive Drawing Oerations Digital Concets of Drawing in Raster Arras PIXEL is a single arra element at x, - No smaller drawing unit exists Px,
CS335 Fall 007 Grahics and Multimedia D Drawings: Lines Primitive Drawing Oerations Digital Concets of Drawing in Raster Arras PIXEL is a single arra element at x, - No smaller drawing unit exists Px,
CS 372: Computational Geometry Lecture 3 Line Segment Intersection
 CS 372: Computational Geometry Lecture 3 Line Segment Intersection Antoine Vigneron King Abdullah University of Science and Technology September 9, 2012 Antoine Vigneron (KAUST) CS 372 Lecture 3 September
CS 372: Computational Geometry Lecture 3 Line Segment Intersection Antoine Vigneron King Abdullah University of Science and Technology September 9, 2012 Antoine Vigneron (KAUST) CS 372 Lecture 3 September
CSCE 411 Design and Analysis of Algorithms
 CSCE 411 Design and Analysis of Algorithms Set 3: Divide and Conquer Slides by Prof. Jennifer Welch Spring 2014 CSCE 411, Spring 2014: Set 3 1 General Idea of Divide & Conquer 1. Take your problem and
CSCE 411 Design and Analysis of Algorithms Set 3: Divide and Conquer Slides by Prof. Jennifer Welch Spring 2014 CSCE 411, Spring 2014: Set 3 1 General Idea of Divide & Conquer 1. Take your problem and
CS 6463: AT Computational Geometry Spring 2006 Convex Hulls Carola Wenk
 CS 6463: AT Computational Geometry Spring 2006 Convex Hulls Carola Wenk 8/29/06 CS 6463: AT Computational Geometry 1 Convex Hull Problem Given a set of pins on a pinboard and a rubber band around them.
CS 6463: AT Computational Geometry Spring 2006 Convex Hulls Carola Wenk 8/29/06 CS 6463: AT Computational Geometry 1 Convex Hull Problem Given a set of pins on a pinboard and a rubber band around them.
Flavor of Computational Geometry. Convex Hull in 2D. Shireen Y. Elhabian Aly A. Farag University of Louisville
 Flavor of Computational Geometry Convex Hull in 2D Shireen Y. Elhabian Aly A. Farag University of Louisville February 2010 Agenda Introduction Definitions of Convexity and Convex Hulls Naïve Algorithms
Flavor of Computational Geometry Convex Hull in 2D Shireen Y. Elhabian Aly A. Farag University of Louisville February 2010 Agenda Introduction Definitions of Convexity and Convex Hulls Naïve Algorithms
3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College
![3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College 3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College](/thumbs/90/102029124.jpg) 3D convex hulls Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hulls The problem: Given a set P of points, compute their convex hull 2D 3D 2D 3D polygon polyhedron Polyhedron region
3D convex hulls Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hulls The problem: Given a set P of points, compute their convex hull 2D 3D 2D 3D polygon polyhedron Polyhedron region
Curve Reconstruction taken from [1]
![Curve Reconstruction taken from [1] Curve Reconstruction taken from [1]](/thumbs/95/124183256.jpg) Notes by Tamal K. Dey, OSU 47 Curve Reconstruction taken from [1] The simlest class of manifolds that ose nontrivial reconstruction roblems are curves in the lane. We will describe two algorithms for curve
Notes by Tamal K. Dey, OSU 47 Curve Reconstruction taken from [1] The simlest class of manifolds that ose nontrivial reconstruction roblems are curves in the lane. We will describe two algorithms for curve
Computational Geometry. HKU ACM ICPC Training 2010
 Computational Geometry HKU ACM ICPC Training 2010 1 What is Computational Geometry? Deals with geometrical structures Points, lines, line segments, vectors, planes, etc. A relatively boring class of problems
Computational Geometry HKU ACM ICPC Training 2010 1 What is Computational Geometry? Deals with geometrical structures Points, lines, line segments, vectors, planes, etc. A relatively boring class of problems
COP 4531 Complexity & Analysis of Data Structures & Algorithms
 COP 4531 Complexity & Analysis of Data Structures & Algorithms Amortized Analysis Thanks to the text authors who contributed to these slides What is amortized analysis? Analyze a sequence of operations
COP 4531 Complexity & Analysis of Data Structures & Algorithms Amortized Analysis Thanks to the text authors who contributed to these slides What is amortized analysis? Analyze a sequence of operations
Computational Geometry Algorithmische Geometrie
 Algorithmische Geometrie Panos Giannopoulos Wolfgang Mulzer Lena Schlipf AG TI SS 2013 !! Register in Campus Management!! Outline What you need to know (before taking this course) What is the course about?
Algorithmische Geometrie Panos Giannopoulos Wolfgang Mulzer Lena Schlipf AG TI SS 2013 !! Register in Campus Management!! Outline What you need to know (before taking this course) What is the course about?
CSC Design and Analysis of Algorithms
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
Deformable Free Space Tilings for Kinetic Collision Detection
 Deformable Free Sace Tilings for Kinetic Collision Detection Pankaj K. Agarwal Julien Basch Leonidas J. Guibas John Hershberger Li Zhang Abstract We resent kinetic data structures for detecting collisions
Deformable Free Sace Tilings for Kinetic Collision Detection Pankaj K. Agarwal Julien Basch Leonidas J. Guibas John Hershberger Li Zhang Abstract We resent kinetic data structures for detecting collisions
Lecture 7: Computational Geometry
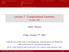 Lecture 7: Computational Geometry CS 491 CAP Uttam Thakore Friday, October 7 th, 2016 Credit for many of the slides on solving geometry problems goes to the Stanford CS 97SI course lecture on computational
Lecture 7: Computational Geometry CS 491 CAP Uttam Thakore Friday, October 7 th, 2016 Credit for many of the slides on solving geometry problems goes to the Stanford CS 97SI course lecture on computational
The Spatial Skyline Queries
 The Satial Skyline Queries Mehdi Sharifzadeh Comuter Science Deartment University of Southern California Los Angeles, CA 90089-078 sharifza@usc.edu Cyrus Shahabi Comuter Science Deartment University of
The Satial Skyline Queries Mehdi Sharifzadeh Comuter Science Deartment University of Southern California Los Angeles, CA 90089-078 sharifza@usc.edu Cyrus Shahabi Comuter Science Deartment University of
2D Geometry. Pierre Alliez Inria Sophia Antipolis
 2D Geometry Pierre Alliez Inria Sophia Antipolis Outline Sample problems Polygons Graphs Convex hull Voronoi diagram Delaunay triangulation Sample Problems Line Segment Intersection Theorem: Segments (p
2D Geometry Pierre Alliez Inria Sophia Antipolis Outline Sample problems Polygons Graphs Convex hull Voronoi diagram Delaunay triangulation Sample Problems Line Segment Intersection Theorem: Segments (p
The convex hull of a set Q of points is the smallest convex polygon P for which each point in Q is either on the boundary of P or in its interior.
 CS 312, Winter 2007 Project #1: Convex Hull Due Dates: See class schedule Overview: In this project, you will implement a divide and conquer algorithm for finding the convex hull of a set of points and
CS 312, Winter 2007 Project #1: Convex Hull Due Dates: See class schedule Overview: In this project, you will implement a divide and conquer algorithm for finding the convex hull of a set of points and
CSE 546, Fall, 2016 Homework 1
 CSE 546, Fall, 2016 Homework 1 Due at the beginning of class Thursday, Sept. 15 at 2:30pm. Accepted without penalty until Friday, noon, in my mailbox in the Dept. office, third floor of Jolley. Notes about
CSE 546, Fall, 2016 Homework 1 Due at the beginning of class Thursday, Sept. 15 at 2:30pm. Accepted without penalty until Friday, noon, in my mailbox in the Dept. office, third floor of Jolley. Notes about
Geometry. Zachary Friggstad. Programming Club Meeting
 Geometry Zachary Friggstad Programming Club Meeting Points #i n c l u d e typedef complex p o i n t ; p o i n t p ( 1. 0, 5. 7 ) ; p. r e a l ( ) ; // x component p. imag ( ) ; // y component
Geometry Zachary Friggstad Programming Club Meeting Points #i n c l u d e typedef complex p o i n t ; p o i n t p ( 1. 0, 5. 7 ) ; p. r e a l ( ) ; // x component p. imag ( ) ; // y component
Lecture 1: September 6, 2001
 Lecture 1: September 6, 2001 Welcome to 6.838J, Geometric Computation! Introductions Overview and Goals General Information Syllabus 2D Convex Hull Signup sheets (return by end of class) MIT 6.838J/4.214J
Lecture 1: September 6, 2001 Welcome to 6.838J, Geometric Computation! Introductions Overview and Goals General Information Syllabus 2D Convex Hull Signup sheets (return by end of class) MIT 6.838J/4.214J
CS 450: COMPUTER GRAPHICS 2D TRANSFORMATIONS SPRING 2016 DR. MICHAEL J. REALE
 CS 45: COMUTER GRAHICS 2D TRANSFORMATIONS SRING 26 DR. MICHAEL J. REALE INTRODUCTION Now that we hae some linear algebra under our resectie belts, we can start ug it in grahics! So far, for each rimitie,
CS 45: COMUTER GRAHICS 2D TRANSFORMATIONS SRING 26 DR. MICHAEL J. REALE INTRODUCTION Now that we hae some linear algebra under our resectie belts, we can start ug it in grahics! So far, for each rimitie,
Recognizing Convex Polygons with Few Finger Probes
 Pattern Analysis and Alications manuscrit No. (will be inserted by the editor) Recognizing Convex Polygons with Few Finger Probes Sumanta Guha Kiêu Trọng Khánh Received: date / Acceted: date Abstract The
Pattern Analysis and Alications manuscrit No. (will be inserted by the editor) Recognizing Convex Polygons with Few Finger Probes Sumanta Guha Kiêu Trọng Khánh Received: date / Acceted: date Abstract The
Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here)
 Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here) Voronoi Diagram & Delaunay Triangualtion Algorithms Divide-&-Conquer Plane Sweep Lifting
Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here) Voronoi Diagram & Delaunay Triangualtion Algorithms Divide-&-Conquer Plane Sweep Lifting
Chapter 3: Graphics Output Primitives. OpenGL Line Functions. OpenGL Point Functions. Line Drawing Algorithms
 Chater : Grahics Outut Primitives Primitives: functions in grahics acage that we use to describe icture element Points and straight lines are the simlest rimitives Some acages include circles, conic sections,
Chater : Grahics Outut Primitives Primitives: functions in grahics acage that we use to describe icture element Points and straight lines are the simlest rimitives Some acages include circles, conic sections,
CSC Design and Analysis of Algorithms. Lecture 6. Divide and Conquer Algorithm Design Technique. Divide-and-Conquer
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
A Concise Workbook for College Algebra
 City University of New York (CUNY) CUNY Academic Works Oen Educational Resources Queensborough Community College Summer 6--08 A Concise Workbook for College Algebra Fei Ye Queensborough Community College
City University of New York (CUNY) CUNY Academic Works Oen Educational Resources Queensborough Community College Summer 6--08 A Concise Workbook for College Algebra Fei Ye Queensborough Community College
Polygon Partitioning. Lecture03
 1 Polygon Partitioning Lecture03 2 History of Triangulation Algorithms 3 Outline Monotone polygon Triangulation of monotone polygon Trapezoidal decomposition Decomposition in monotone mountain Convex decomposition
1 Polygon Partitioning Lecture03 2 History of Triangulation Algorithms 3 Outline Monotone polygon Triangulation of monotone polygon Trapezoidal decomposition Decomposition in monotone mountain Convex decomposition
Chapter 4. Divide-and-Conquer. Copyright 2007 Pearson Addison-Wesley. All rights reserved.
 Chapter 4 Divide-and-Conquer Copyright 2007 Pearson Addison-Wesley. All rights reserved. Divide-and-Conquer The most-well known algorithm design strategy: 2. Divide instance of problem into two or more
Chapter 4 Divide-and-Conquer Copyright 2007 Pearson Addison-Wesley. All rights reserved. Divide-and-Conquer The most-well known algorithm design strategy: 2. Divide instance of problem into two or more
High-Dimensional Computational Geometry. Jingbo Shang University of Illinois at Urbana-Champaign Mar 5, 2018
 High-Dimensional Computational Geometry Jingbo Shang University of Illinois at Urbana-Champaign Mar 5, 2018 Outline 3-D vector geometry High-D hyperplane intersections Convex hull & its extension to 3
High-Dimensional Computational Geometry Jingbo Shang University of Illinois at Urbana-Champaign Mar 5, 2018 Outline 3-D vector geometry High-D hyperplane intersections Convex hull & its extension to 3
Divide-and-Conquer. The most-well known algorithm design strategy: smaller instances. combining these solutions
 Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original
Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original
3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College
![3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College 3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College](/thumbs/75/72944672.jpg) 3D convex hulls Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull in 3D The problem: Given a set P of points in 3D, compute their convex hull convex polyhedron 2D 3D polygon
3D convex hulls Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull in 3D The problem: Given a set P of points in 3D, compute their convex hull convex polyhedron 2D 3D polygon
Computational Geometry
 Lecture 12: Lecture 12: Motivation: Terrains by interpolation To build a model of the terrain surface, we can start with a number of sample points where we know the height. Lecture 12: Motivation: Terrains
Lecture 12: Lecture 12: Motivation: Terrains by interpolation To build a model of the terrain surface, we can start with a number of sample points where we know the height. Lecture 12: Motivation: Terrains
CS2 Algorithms and Data Structures Note 8
 CS2 Algorithms and Data Structures Note 8 Heasort and Quicksort We will see two more sorting algorithms in this lecture. The first, heasort, is very nice theoretically. It sorts an array with n items in
CS2 Algorithms and Data Structures Note 8 Heasort and Quicksort We will see two more sorting algorithms in this lecture. The first, heasort, is very nice theoretically. It sorts an array with n items in
In what follows, we will focus on Voronoi diagrams in Euclidean space. Later, we will generalize to other distance spaces.
 Voronoi Diagrams 4 A city builds a set of post offices, and now needs to determine which houses will be served by which office. It would be wasteful for a postman to go out of their way to make a delivery
Voronoi Diagrams 4 A city builds a set of post offices, and now needs to determine which houses will be served by which office. It would be wasteful for a postman to go out of their way to make a delivery
split split (a) (b) split split (c) (d)
 International Journal of Foundations of Comuter Science c World Scientic Publishing Comany ON COST-OPTIMAL MERGE OF TWO INTRANSITIVE SORTED SEQUENCES JIE WU Deartment of Comuter Science and Engineering
International Journal of Foundations of Comuter Science c World Scientic Publishing Comany ON COST-OPTIMAL MERGE OF TWO INTRANSITIVE SORTED SEQUENCES JIE WU Deartment of Comuter Science and Engineering
Using Rational Numbers and Parallel Computing to Efficiently Avoid Round-off Errors on Map Simplification
 Using Rational Numbers and Parallel Comuting to Efficiently Avoid Round-off Errors on Ma Simlification Maurício G. Grui 1, Salles V. G. de Magalhães 1,2, Marcus V. A. Andrade 1, W. Randolh Franklin 2,
Using Rational Numbers and Parallel Comuting to Efficiently Avoid Round-off Errors on Ma Simlification Maurício G. Grui 1, Salles V. G. de Magalhães 1,2, Marcus V. A. Andrade 1, W. Randolh Franklin 2,
Flavor of Computational Geometry. Voronoi Diagrams. Shireen Y. Elhabian Aly A. Farag University of Louisville
 Flavor of Computational Geometry Voronoi Diagrams Shireen Y. Elhabian Aly A. Farag University of Louisville March 2010 Pepperoni Sparse Pizzas Olive Sparse Pizzas Just Two Pepperonis A person gets the
Flavor of Computational Geometry Voronoi Diagrams Shireen Y. Elhabian Aly A. Farag University of Louisville March 2010 Pepperoni Sparse Pizzas Olive Sparse Pizzas Just Two Pepperonis A person gets the
CS 373: Combinatorial Algorithms, Fall Name: Net ID: Alias: U 3 / 4 1
 CS 373: Combinatorial Algorithms, Fall 2000 Homework 1 (due November 16, 2000 at midnight) Starting with Homework 1, homeworks may be done in teams of up to three people. Each team turns in just one solution,
CS 373: Combinatorial Algorithms, Fall 2000 Homework 1 (due November 16, 2000 at midnight) Starting with Homework 1, homeworks may be done in teams of up to three people. Each team turns in just one solution,
Preferred directions for resolving the non-uniqueness of Delaunay triangulations
 Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
Voronoi Diagrams. A Voronoi diagram records everything one would ever want to know about proximity to a set of points
 Voronoi Diagrams Voronoi Diagrams A Voronoi diagram records everything one would ever want to know about proximity to a set of points Who is closest to whom? Who is furthest? We will start with a series
Voronoi Diagrams Voronoi Diagrams A Voronoi diagram records everything one would ever want to know about proximity to a set of points Who is closest to whom? Who is furthest? We will start with a series
Week 8 Voronoi Diagrams
 1 Week 8 Voronoi Diagrams 2 Voronoi Diagram Very important problem in Comp. Geo. Discussed back in 1850 by Dirichlet Published in a paper by Voronoi in 1908 3 Voronoi Diagram Fire observation towers: an
1 Week 8 Voronoi Diagrams 2 Voronoi Diagram Very important problem in Comp. Geo. Discussed back in 1850 by Dirichlet Published in a paper by Voronoi in 1908 3 Voronoi Diagram Fire observation towers: an
Closest Pair of Points. Cormen et.al 33.4
 Closest Pair of Points Cormen et.al 33.4 Closest Pair of Points Closest pair. Given n points in the plane, find a pair with smallest Euclidean distance between them. Fundamental geometric problem. Graphics,
Closest Pair of Points Cormen et.al 33.4 Closest Pair of Points Closest pair. Given n points in the plane, find a pair with smallest Euclidean distance between them. Fundamental geometric problem. Graphics,
Simple example. Analysis of programs with pointers. Points-to relation. Program model. Points-to graph. Ordering on points-to relation
 Simle eamle Analsis of rograms with ointers := 5 tr := @ *tr := 9 := rogram S1 S2 S3 S4 deendences What are the deendences in this rogram? Problem: just looking at variable names will not give ou the correct
Simle eamle Analsis of rograms with ointers := 5 tr := @ *tr := 9 := rogram S1 S2 S3 S4 deendences What are the deendences in this rogram? Problem: just looking at variable names will not give ou the correct
Clipping. Administrative. Assignment 1 Gallery. Questions about previous lectures? Overview of graphics pipeline? Assignment 2
 Cliing MIT EECS 6.837 Frédo Durand and Seth Teller Some slides and images courtesy of Leonard McMillan MIT EECS 6.837, Teller and Durand 1 MIT EECS 6.837, Teller and Durand 2 Administrative Assignment
Cliing MIT EECS 6.837 Frédo Durand and Seth Teller Some slides and images courtesy of Leonard McMillan MIT EECS 6.837, Teller and Durand 1 MIT EECS 6.837, Teller and Durand 2 Administrative Assignment
Analysis of Algorithms. Unit 4 - Analysis of well known Algorithms
 Analysis of Algorithms Unit 4 - Analysis of well known Algorithms 1 Analysis of well known Algorithms Brute Force Algorithms Greedy Algorithms Divide and Conquer Algorithms Decrease and Conquer Algorithms
Analysis of Algorithms Unit 4 - Analysis of well known Algorithms 1 Analysis of well known Algorithms Brute Force Algorithms Greedy Algorithms Divide and Conquer Algorithms Decrease and Conquer Algorithms
Dr Pavan Chakraborty IIIT-Allahabad
 GVC-43 Lecture - 5 Ref: Donald Hearn & M. Pauline Baker, Comuter Grahics Foley, van Dam, Feiner & Hughes, Comuter Grahics Princiles & Practice Dr Pavan Chakraborty IIIT-Allahabad Summary of line drawing
GVC-43 Lecture - 5 Ref: Donald Hearn & M. Pauline Baker, Comuter Grahics Foley, van Dam, Feiner & Hughes, Comuter Grahics Princiles & Practice Dr Pavan Chakraborty IIIT-Allahabad Summary of line drawing
Geometric Dilation. A polygonal chain C. detour of C on the pair (p, q): where C q p the path on C connecting p and q. detour of C
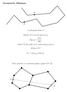 Geometric Dilation A olygonal chain C detour of C on the air (, ): δ(, ) = C, where C the ath on C connecting and. detour of C δ C = max, C δ(, ). More general: A connected lanar grah G(V, E) Gemetric
Geometric Dilation A olygonal chain C detour of C on the air (, ): δ(, ) = C, where C the ath on C connecting and. detour of C δ C = max, C δ(, ). More general: A connected lanar grah G(V, E) Gemetric
Notes in Computational Geometry Voronoi Diagrams
 Notes in Computational Geometry Voronoi Diagrams Prof. Sandeep Sen and Prof. Amit Kumar Indian Institute of Technology, Delhi Voronoi Diagrams In this lecture, we study Voronoi Diagrams, also known as
Notes in Computational Geometry Voronoi Diagrams Prof. Sandeep Sen and Prof. Amit Kumar Indian Institute of Technology, Delhi Voronoi Diagrams In this lecture, we study Voronoi Diagrams, also known as
Randomized algorithms: Two examples and Yao s Minimax Principle
 Randomized algorithms: Two examles and Yao s Minimax Princile Maximum Satisfiability Consider the roblem Maximum Satisfiability (MAX-SAT). Bring your knowledge u-to-date on the Satisfiability roblem. Maximum
Randomized algorithms: Two examles and Yao s Minimax Princile Maximum Satisfiability Consider the roblem Maximum Satisfiability (MAX-SAT). Bring your knowledge u-to-date on the Satisfiability roblem. Maximum
CS 548: COMPUTER GRAPHICS DRAWING LINES AND CIRCLES SPRING 2015 DR. MICHAEL J. REALE
 CS 548: COMPUTER GRAPHICS DRAWING LINES AND CIRCLES SPRING 05 DR. MICHAEL J. REALE OPENGL POINTS AND LINES OPENGL POINTS AND LINES In OenGL, there are different constants used to indicate what ind of rimitive
CS 548: COMPUTER GRAPHICS DRAWING LINES AND CIRCLES SPRING 05 DR. MICHAEL J. REALE OPENGL POINTS AND LINES OPENGL POINTS AND LINES In OenGL, there are different constants used to indicate what ind of rimitive
Parallel Construction of Multidimensional Binary Search Trees. Ibraheem Al-furaih, Srinivas Aluru, Sanjay Goil Sanjay Ranka
 Parallel Construction of Multidimensional Binary Search Trees Ibraheem Al-furaih, Srinivas Aluru, Sanjay Goil Sanjay Ranka School of CIS and School of CISE Northeast Parallel Architectures Center Syracuse
Parallel Construction of Multidimensional Binary Search Trees Ibraheem Al-furaih, Srinivas Aluru, Sanjay Goil Sanjay Ranka School of CIS and School of CISE Northeast Parallel Architectures Center Syracuse
CMSC 754 Computational Geometry 1
 CMSC 754 Computational Geometry 1 David M. Mount Department of Computer Science University of Maryland Spring 2007 1 Copyright, David M. Mount, 2007, Dept. of Computer Science, University of Maryland,
CMSC 754 Computational Geometry 1 David M. Mount Department of Computer Science University of Maryland Spring 2007 1 Copyright, David M. Mount, 2007, Dept. of Computer Science, University of Maryland,
Lecture 2: Divide and Conquer
 Lecture 2: Divide and Conquer Paradigm Convex Hull Median finding Paradigm Given a problem of size n divide it into subproblems of size n, a 1, b >1. Solve each b subproblem recursively. Combine solutions
Lecture 2: Divide and Conquer Paradigm Convex Hull Median finding Paradigm Given a problem of size n divide it into subproblems of size n, a 1, b >1. Solve each b subproblem recursively. Combine solutions
Coarse grained gather and scatter operations with applications
 Available online at www.sciencedirect.com J. Parallel Distrib. Comut. 64 (2004) 1297 1310 www.elsevier.com/locate/jdc Coarse grained gather and scatter oerations with alications Laurence Boxer a,b,, Russ
Available online at www.sciencedirect.com J. Parallel Distrib. Comut. 64 (2004) 1297 1310 www.elsevier.com/locate/jdc Coarse grained gather and scatter oerations with alications Laurence Boxer a,b,, Russ
Computational Geometry
 Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
