COT5405: GEOMETRIC ALGORITHMS
|
|
|
- Emery Dennis
- 6 years ago
- Views:
Transcription
1 COT5405: GEOMETRIC ALGORITHMS Objects: Points in, Segments, Lines, Circles, Triangles Polygons, Polyhedra R n Alications Vision, Grahics, Visualizations, Databases, Data mining, Networks, GIS Scientific Comuting, Engineering, CAD Com Biology, Physics simulations, Oerations research, Prof. Aler Ungor - An Short Introduction to Comutational Geometry
2 SAMPLE PROBLEMS / CONCEPTS Convex Hulls or the unique convex olygon that contains P and whose vertices are al P might have interior oints that are not vertices of the convex hull. Triangulations? Voronoi diagram Motivation Voronoi diagrams Voronoi diagrams Satial interolation A set of oints and its convex hull. Convex hull vertices are black; interior oints are white. Nearest Neighborhood Diagrams Geometric decision Intersections to list vertices counterclockwise instead of clockwise is arbitrary Comutational Geometry Lecture 10: Voronoi diagrams To simlify the resentation of the convex hull algorithms, I will assu Range Queries Just to make things concrete, we will reresent the oints in P by th in two arrays X[1.. n] and Y [1.. n]. We will reresent the convex hull vertices in counterclockwise order. if the ith oint is a vertex of the conv the next vertex counterclockwise and red[i] is the index of the next ve next[i] = red[i] = 0. It doesn t matter which vertex we choose as th general osition, meaning (in this context) that no three oints lie on a like assuming that no two elements are equal when we talk about sorting to really imlement these algorithms, we would have to handle colinear t consistently. This is fairly easy, but definitely not trivial. E.2 Simle Cases
3 CONVEX HULLS Convex Hull, CH(P), of a set of oints P is the smallest convex olygon that contains P largest convex olygon whose vertices are all oints in P unique convex olygon that contains P and whose vertices are all oints in P
4 CONVEXITY A set C IR d is convex iff (, q) C 2 the line segment q is contained in C. q q Convex Non convex
5 CONVEX HULL PROBLEM Inut: the set P = { 1, 2,... n } IR 2 Outut: a sequence L = (c 1, c 2,... c h ) of vertices of CH(P ) in counterclockwise order Examle: L = ( 3, 4, 8, 6, 1, 5 ) CH(P )
6 CONVEX HULL - Characterization The directed edge (, q) is an edge of CH(P ) iff q CH(P )
7 CONVEX HULL - Characterization The directed edge (, q) is an edge of CH(P ) iff q r all r P \ {, q} lies to the left of line q (oriented by q).
8 CONVEX HULL PROBLEM The directed edge (, q) is an edge of CH(P ) iff q r r P \ {, q} the triangle (, q, r) is oriented counterclockwise.
9 CONVEX HULL We denote CCW (, q, r) = x x q x r y y q y r = (x q x )(y r y ) (x r x )(y q y ) Triangle (, q, r) is counterclockwise iff CCW (, q, r) > 0. How fast can we erform this test? 2 multilications and 5 subtractions takes O(1) time
10 CONVEX HULL - Naive Algorithm Algorithm SlowConvexHull(P) Inut: a set P of oints in IR 2 Outut: CH(P ) 1. E P 2 2. for all (, q, r) P 3 such that r / {, q} 3. if CCW (, q, r) 0 4. then remove (, q) from E 5. Write the remaining edges of E into L in counterclockwise order 6. Return L
11 CONVEX HULL - Divide & Conquer Comute median in x-coordinate and Slit P into two sets Comute Left and Right Hulls recursively Merge the two Hulls q q q q q q
12 CONVEX HULL - Gift Wraing Start with the leftmost oint and wra around =l l l l l l The execution of Jarvis s March.
13 CONVEX HULL - Gift Wraing JarvisMarch(X[1.. n], Y [1.. n]): l 1 for i 2 to n if X[i] < X[l] l i l reeat q + 1 Make sure q for i 2 to n if CCW(, i, q) q i next[] q; rev[q] q until = l
14 CONVEX HULL - Lower Bound let N = (x 1, x 2,... x n ) IR for all i let i = (x i, x 2 i ) comute CH(P ) P : y = x 2 CH(P )
15 Line-segment intersection Given n line segments, does any air intersect? a d e c b f
16 Line-segment intersection Given n line segments, does any air intersect? Obvious algorithm: O(n 2 ). e d a c b f
17 Swee-line algorithm Swee a vertical line from left to right (concetually relacing x-coordinate with time). Maintain dynamic set S of segments that intersect the swee line, ordered (tentatively) by y-coordinate of intersection. Order changes when new segment is encountered, existing segment finishes, or two segments cross segment endoints Key event oints are therefore segment endoints.
18 d e e e b a a a d d e d b e e c c c c d b d d d a b b b b b b f f f f a d e c b f
19 Swee-line algorithm Process event oints in order by sorting segment endoints by x-coordinate and looing through: For a left endoint of segment s: Add segment s to dynamic set S. Check for intersection between s and its neighbors in S. For a right endoint of segment s: Remove segment s from dynamic set S. Check for intersection between the neighbors of s in S.
20 Analysis Use red-black tree to store dynamic set S. Total running time: O(n lg n).
21 Correctness Theorem: If there is an intersection, the algorithm finds it.
22 Correctness Theorem: If there is an intersection, the algorithm finds it. Proof: Let X be the leftmost intersection oint. Assume for simlicity that only two segments s 1, s 2 ass through X, and no two oints have the same x-coordinate. At some oint before we reach X, s 1 and s 2 become consecutive in the order of S. Either initially consecutive when s 1 or s 2 inserted, or became consecutive when another deleted.
23 Closest Pair Find a closest air among 1 n!r d Easy to do in O(dn 2 ) time For all i j, comute i j and choose the minimum We will aim for better time, as long as d is small For now, focus on d=2
24 Divide & Conquer Divide: Comute the median of x- coordinates Slit the oints into P L and P R, each of size n/2 Conquer: comute the closest airs for P L and P R Combine the results (the hard art)
25 Divide & Conquer Combine 2k Let k=min(k 1,k 2 ) Observe: Need to check only airs which cross the dividing line Only interested in airs within distance < k Suffices to look at oints in the 2k-width stri around the median line k 1 k 2
26 Divide & Conquer Scanning the stri Sort all oints in the stri by their y-coordinates, forming q 1 q r, r n. Let y i be the y-coordinate of q i For i=1 to r j=i-1 While y i -y j < d Check the air q i,q j j:=j-1 d
27 Divide & Conquer - Analysis Correctness: easy Running time is more involved k Can we have many q j s that are within distance k from q i? No Proof by acking argument
28 Divide & Conquer - Analysis Theorem: there are at most 7 q j s such that y i -y j k. Proof: Each such q j must lie either in the left or in the right k! k square Within each square, all oints have distance distance k from others We can ack at most 4 such oints into one square, so we have 8 oints total (incl. q i ) q i
29 Divide & Conquer - Analysis Packing bound Proving 4 is not obvious Will rove 5 Draw a disk of radius k/2 around each oint Disks are disjoint The disk-square intersection has area (k/2)2/4 = /16 k2 The square has area k2 Can ack at most 16/ 5.1 oints
30 Divide & Conquer - Analysis Running time Divide: O(n) Combine: O(n log n) because we sort by y However, we can: Sort all oints by y at the beginning Divide reserves the y-order of oints Then combine takes only O(n) We get T(n)=2T(n/2)+O(n), so T(n)=O(n log n)
Cross products. p 2 p. p p1 p2. p 1. Line segments The convex combination of two distinct points p1 ( x1, such that for some real number with 0 1,
 CHAPTER 33 Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
CHAPTER 33 Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
Cross products Line segments The convex combination of two distinct points p
 CHAPTER Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
CHAPTER Comutational Geometry Is the branch of comuter science that studies algorithms for solving geometric roblems. Has alications in many fields, including comuter grahics robotics, VLSI design comuter
Graduate Algorithms CS F-19 Computational Geometry
 Graduate Algorithms CS673-016F-19 Comutational Geometry David Galles Deartment of Comuter Science University of San Francisco 19-0: Cross Products Given any two oints 1 = (x 1,y 1 ) and = (x,y ) Cross
Graduate Algorithms CS673-016F-19 Comutational Geometry David Galles Deartment of Comuter Science University of San Francisco 19-0: Cross Products Given any two oints 1 = (x 1,y 1 ) and = (x,y ) Cross
Convex Hulls. Helen Cameron. Helen Cameron Convex Hulls 1/101
 Convex Hulls Helen Cameron Helen Cameron Convex Hulls 1/101 What Is a Convex Hull? Starting Point: Points in 2D y x Helen Cameron Convex Hulls 3/101 Convex Hull: Informally Imagine that the x, y-lane is
Convex Hulls Helen Cameron Helen Cameron Convex Hulls 1/101 What Is a Convex Hull? Starting Point: Points in 2D y x Helen Cameron Convex Hulls 3/101 Convex Hull: Informally Imagine that the x, y-lane is
Computational Geometry
 Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Geometric Computation: Introduction. Piotr Indyk
 Geometric Computation: Introduction Piotr Indyk Welcome to 6.850! Overview and goals Course Information Closest pair Signup sheet Geometric Computation Geometric computation occurs everywhere: Robotics:
Geometric Computation: Introduction Piotr Indyk Welcome to 6.850! Overview and goals Course Information Closest pair Signup sheet Geometric Computation Geometric computation occurs everywhere: Robotics:
Computational Geometry. Lecture 17
 Computational Geometry Lecture 17 Computational geometry Algorithms for solving geometric problems in 2D and higher. Fundamental objects: Basic structures: point line segment line point set polygon L17.2
Computational Geometry Lecture 17 Computational geometry Algorithms for solving geometric problems in 2D and higher. Fundamental objects: Basic structures: point line segment line point set polygon L17.2
Lecture 3: Geometric Algorithms(Convex sets, Divide & Conquer Algo.)
 Advanced Algorithms Fall 2015 Lecture 3: Geometric Algorithms(Convex sets, Divide & Conuer Algo.) Faculty: K.R. Chowdhary : Professor of CS Disclaimer: These notes have not been subjected to the usual
Advanced Algorithms Fall 2015 Lecture 3: Geometric Algorithms(Convex sets, Divide & Conuer Algo.) Faculty: K.R. Chowdhary : Professor of CS Disclaimer: These notes have not been subjected to the usual
Lecture 8: Orthogonal Range Searching
 CPS234 Comutational Geometry Setember 22nd, 2005 Lecture 8: Orthogonal Range Searching Lecturer: Pankaj K. Agarwal Scribe: Mason F. Matthews 8.1 Range Searching The general roblem of range searching is
CPS234 Comutational Geometry Setember 22nd, 2005 Lecture 8: Orthogonal Range Searching Lecturer: Pankaj K. Agarwal Scribe: Mason F. Matthews 8.1 Range Searching The general roblem of range searching is
CS 532: 3D Computer Vision 14 th Set of Notes
 1 CS 532: 3D Computer Vision 14 th Set of Notes Instructor: Philippos Mordohai Webpage: www.cs.stevens.edu/~mordohai E-mail: Philippos.Mordohai@stevens.edu Office: Lieb 215 Lecture Outline Triangulating
1 CS 532: 3D Computer Vision 14 th Set of Notes Instructor: Philippos Mordohai Webpage: www.cs.stevens.edu/~mordohai E-mail: Philippos.Mordohai@stevens.edu Office: Lieb 215 Lecture Outline Triangulating
Computational Geometry
 Motivation Motivation Polygons and visibility Visibility in polygons Triangulation Proof of the Art gallery theorem Two points in a simple polygon can see each other if their connecting line segment is
Motivation Motivation Polygons and visibility Visibility in polygons Triangulation Proof of the Art gallery theorem Two points in a simple polygon can see each other if their connecting line segment is
Polygon Triangulation. (slides partially by Daniel Vlasic )
 Polygon Triangulation (slides partially by Daniel Vlasic ) Triangulation: Definition Triangulation of a simple polygon P: decomposition of P into triangles by a maximal set of non-intersecting diagonals
Polygon Triangulation (slides partially by Daniel Vlasic ) Triangulation: Definition Triangulation of a simple polygon P: decomposition of P into triangles by a maximal set of non-intersecting diagonals
1/60. Geometric Algorithms. Lecture 1: Introduction. Convex Hulls
 1/60 Geometric Algorithms Lecture 1: Introduction Convex Hulls Geometric algorithms scope 2/60 Geometry algorithms (practice): Study of geometric problems that arise in various applications and how algorithms
1/60 Geometric Algorithms Lecture 1: Introduction Convex Hulls Geometric algorithms scope 2/60 Geometry algorithms (practice): Study of geometric problems that arise in various applications and how algorithms
Convex Hull Algorithms
 Convex Hull Algorithms Design and Analysis of Algorithms prof. F. Malucelli Villa Andrea e Ceriani Simone Outline Problem Definition Basic Concepts Bruteforce Algorithm Graham Scan Algorithm Divide and
Convex Hull Algorithms Design and Analysis of Algorithms prof. F. Malucelli Villa Andrea e Ceriani Simone Outline Problem Definition Basic Concepts Bruteforce Algorithm Graham Scan Algorithm Divide and
We will then introduce the DT, discuss some of its fundamental properties and show how to compute a DT directly from a given set of points.
 Voronoi Diagram and Delaunay Triangulation 1 Introduction The Voronoi Diagram (VD, for short) is a ubiquitious structure that aears in a variety of discilines - biology, geograhy, ecology, crystallograhy,
Voronoi Diagram and Delaunay Triangulation 1 Introduction The Voronoi Diagram (VD, for short) is a ubiquitious structure that aears in a variety of discilines - biology, geograhy, ecology, crystallograhy,
Computing the Convex Hull of. W. Hochstattler, S. Kromberg, C. Moll
 Reort No. 94.60 A new Linear Time Algorithm for Comuting the Convex Hull of a Simle Polygon in the Plane by W. Hochstattler, S. Kromberg, C. Moll 994 W. Hochstattler, S. Kromberg, C. Moll Universitat zu
Reort No. 94.60 A new Linear Time Algorithm for Comuting the Convex Hull of a Simle Polygon in the Plane by W. Hochstattler, S. Kromberg, C. Moll 994 W. Hochstattler, S. Kromberg, C. Moll Universitat zu
Computational Geometry. Algorithm Design (10) Computational Geometry. Convex Hull. Areas in Computational Geometry
 Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
Polygon Triangulation. (slides partially by Daniel Vlasic )
 Polygon Triangulation (slides partially by Daniel Vlasic ) Triangulation: Definition Triangulation of a simple polygon P: decomposition of P into triangles by a maximal set of non-intersecting diagonals
Polygon Triangulation (slides partially by Daniel Vlasic ) Triangulation: Definition Triangulation of a simple polygon P: decomposition of P into triangles by a maximal set of non-intersecting diagonals
Computational geometry
 Computational geometry Inge Li Gørtz CLRS Chapter 33.0, 33.1, 33.3. Computational Geometry Geometric problems (this course Euclidean plane). Does a set of line segments intersect, dividing plane into regions,
Computational geometry Inge Li Gørtz CLRS Chapter 33.0, 33.1, 33.3. Computational Geometry Geometric problems (this course Euclidean plane). Does a set of line segments intersect, dividing plane into regions,
Polygon decomposition. Motivation: Art gallery problem
 CG Lecture 3 Polygon decomposition 1. Polygon triangulation Triangulation theory Monotone polygon triangulation 2. Polygon decomposition into monotone pieces 3. Trapezoidal decomposition 4. Convex decomposition
CG Lecture 3 Polygon decomposition 1. Polygon triangulation Triangulation theory Monotone polygon triangulation 2. Polygon decomposition into monotone pieces 3. Trapezoidal decomposition 4. Convex decomposition
Week 7 Convex Hulls in 3D
 1 Week 7 Convex Hulls in 3D 2 Polyhedra A polyhedron is the natural generalization of a 2D polygon to 3D 3 Closed Polyhedral Surface A closed polyhedral surface is a finite set of interior disjoint polygons
1 Week 7 Convex Hulls in 3D 2 Polyhedra A polyhedron is the natural generalization of a 2D polygon to 3D 3 Closed Polyhedral Surface A closed polyhedral surface is a finite set of interior disjoint polygons
CSE 5311 Notes 13: Computational Geometry
 CSE 5311 Notes 13: Computational Geometry (Last updated 4/17/17 4:39 PM) SMALLEST ENCLOSING DISK See section 4.7 of de Berg ( http://dx.doi.org.ezproxy.uta.edu/10.1007/978-3-540-77974-2 ) Algorithm MINIDISC(P)
CSE 5311 Notes 13: Computational Geometry (Last updated 4/17/17 4:39 PM) SMALLEST ENCLOSING DISK See section 4.7 of de Berg ( http://dx.doi.org.ezproxy.uta.edu/10.1007/978-3-540-77974-2 ) Algorithm MINIDISC(P)
2D Geometry. Pierre Alliez Inria Sophia Antipolis
 2D Geometry Pierre Alliez Inria Sophia Antipolis Outline Sample problems Polygons Graphs Convex hull Voronoi diagram Delaunay triangulation Sample Problems Line Segment Intersection Theorem: Segments (p
2D Geometry Pierre Alliez Inria Sophia Antipolis Outline Sample problems Polygons Graphs Convex hull Voronoi diagram Delaunay triangulation Sample Problems Line Segment Intersection Theorem: Segments (p
Lecture 2: Fixed-Radius Near Neighbors and Geometric Basics
 structure arises in many alications of geometry. The dual structure, called a Delaunay triangulation also has many interesting roerties. Figure 3: Voronoi diagram and Delaunay triangulation. Search: Geometric
structure arises in many alications of geometry. The dual structure, called a Delaunay triangulation also has many interesting roerties. Figure 3: Voronoi diagram and Delaunay triangulation. Search: Geometric
The convex hull of a set Q of points is the smallest convex polygon P for which each point in Q is either on the boundary of P or in its interior.
 CS 312, Winter 2007 Project #1: Convex Hull Due Dates: See class schedule Overview: In this project, you will implement a divide and conquer algorithm for finding the convex hull of a set of points and
CS 312, Winter 2007 Project #1: Convex Hull Due Dates: See class schedule Overview: In this project, you will implement a divide and conquer algorithm for finding the convex hull of a set of points and
Computational Geometry: Lecture 5
 Computational Geometry: Lecture 5 Don Sheehy January 29, 2010 1 Degeneracy In many of the algorithms that we have discussed so far, we have run into problems when that input is somehow troublesome. For
Computational Geometry: Lecture 5 Don Sheehy January 29, 2010 1 Degeneracy In many of the algorithms that we have discussed so far, we have run into problems when that input is somehow troublesome. For
Voronoi diagram and Delaunay triangulation
 Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Computational Geometry. Geometry Cross Product Convex Hull Problem Sweep Line Algorithm
 GEOMETRY COMP 321 McGill University These slides are mainly compiled from the following resources. - Professor Jaehyun Park slides CS 97SI - Top-coder tutorials. - Programming Challenges books. Computational
GEOMETRY COMP 321 McGill University These slides are mainly compiled from the following resources. - Professor Jaehyun Park slides CS 97SI - Top-coder tutorials. - Programming Challenges books. Computational
Last time. Today: Convex Hull Brute Force Inside(q,abc) Intersect(ab,cd) Orient(a,b,c).
 Last time Convex Hull Brute Force Inside(q,abc) Intersect(ab,cd) Orient(a,b,c). Today: More efficient convex hull algorithms and absolute bounds. Two (of many) algorithms. One (of one) interesting reduction.
Last time Convex Hull Brute Force Inside(q,abc) Intersect(ab,cd) Orient(a,b,c). Today: More efficient convex hull algorithms and absolute bounds. Two (of many) algorithms. One (of one) interesting reduction.
Triangulation and Convex Hull. 8th November 2018
 Triangulation and Convex Hull 8th November 2018 Agenda 1. Triangulation. No book, the slides are the curriculum 2. Finding the convex hull. Textbook, 8.6.2 2 Triangulation and terrain models Here we have
Triangulation and Convex Hull 8th November 2018 Agenda 1. Triangulation. No book, the slides are the curriculum 2. Finding the convex hull. Textbook, 8.6.2 2 Triangulation and terrain models Here we have
CMSC 754 Computational Geometry 1
 CMSC 754 Comutational Geometry 1 David M. Mount Deartment of Comuter Science University of Maryland Fall 2002 1 Coyright, David M. Mount, 2002, Det. of Comuter Science, University of Maryland, College
CMSC 754 Comutational Geometry 1 David M. Mount Deartment of Comuter Science University of Maryland Fall 2002 1 Coyright, David M. Mount, 2002, Det. of Comuter Science, University of Maryland, College
6. Concluding Remarks
 [8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
[8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
An improved algorithm for Hausdorff Voronoi diagram for non-crossing sets
 An imroved algorithm for Hausdorff Voronoi diagram for non-crossing sets Frank Dehne, Anil Maheshwari and Ryan Taylor May 26, 2006 Abstract We resent an imroved algorithm for building a Hausdorff Voronoi
An imroved algorithm for Hausdorff Voronoi diagram for non-crossing sets Frank Dehne, Anil Maheshwari and Ryan Taylor May 26, 2006 Abstract We resent an imroved algorithm for building a Hausdorff Voronoi
Geometric Algorithms. 1. Objects
 Geometric Algorithms 1. Definitions 2. Line-Segment properties 3. Inner Points of polygons 4. Simple polygons 5. Convex hulls 6. Closest pair of points 7. Diameter of a point set 1. Objects 2-dimensional
Geometric Algorithms 1. Definitions 2. Line-Segment properties 3. Inner Points of polygons 4. Simple polygons 5. Convex hulls 6. Closest pair of points 7. Diameter of a point set 1. Objects 2-dimensional
3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College
![3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College 3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College](/thumbs/75/72944672.jpg) 3D convex hulls Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull in 3D The problem: Given a set P of points in 3D, compute their convex hull convex polyhedron 2D 3D polygon
3D convex hulls Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull in 3D The problem: Given a set P of points in 3D, compute their convex hull convex polyhedron 2D 3D polygon
Convex Hulls in Three Dimensions. Polyhedra
 Convex Hulls in Three Dimensions Polyhedra Polyhedron 1.A polyhedron is the generalization of a 2- D polygon to 3-D A finite number of flat polygonal faces The boundary or surface of a polyhedron - Zero-dimensional
Convex Hulls in Three Dimensions Polyhedra Polyhedron 1.A polyhedron is the generalization of a 2- D polygon to 3-D A finite number of flat polygonal faces The boundary or surface of a polyhedron - Zero-dimensional
Notes in Computational Geometry Voronoi Diagrams
 Notes in Computational Geometry Voronoi Diagrams Prof. Sandeep Sen and Prof. Amit Kumar Indian Institute of Technology, Delhi Voronoi Diagrams In this lecture, we study Voronoi Diagrams, also known as
Notes in Computational Geometry Voronoi Diagrams Prof. Sandeep Sen and Prof. Amit Kumar Indian Institute of Technology, Delhi Voronoi Diagrams In this lecture, we study Voronoi Diagrams, also known as
Planar Graphs. 1 Graphs and maps. 1.1 Planarity and duality
 Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Voronoi Diagrams in the Plane. Chapter 5 of O Rourke text Chapter 7 and 9 of course text
 Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
CMSC 425: Lecture 16 Motion Planning: Basic Concepts
 : Lecture 16 Motion lanning: Basic Concets eading: Today s material comes from various sources, including AI Game rogramming Wisdom 2 by S. abin and lanning Algorithms by S. M. LaValle (Chats. 4 and 5).
: Lecture 16 Motion lanning: Basic Concets eading: Today s material comes from various sources, including AI Game rogramming Wisdom 2 by S. abin and lanning Algorithms by S. M. LaValle (Chats. 4 and 5).
Computational Geometry
 CS 5633 -- Spring 2004 Computational Geometry Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 5633 Analysis of Algorithms 1 Computational geometry Algorithms for solving
CS 5633 -- Spring 2004 Computational Geometry Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 5633 Analysis of Algorithms 1 Computational geometry Algorithms for solving
Geometry. Zachary Friggstad. Programming Club Meeting
 Geometry Zachary Friggstad Programming Club Meeting Points #i n c l u d e typedef complex p o i n t ; p o i n t p ( 1. 0, 5. 7 ) ; p. r e a l ( ) ; // x component p. imag ( ) ; // y component
Geometry Zachary Friggstad Programming Club Meeting Points #i n c l u d e typedef complex p o i n t ; p o i n t p ( 1. 0, 5. 7 ) ; p. r e a l ( ) ; // x component p. imag ( ) ; // y component
Lecture 3: Art Gallery Problems and Polygon Triangulation
 EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
CMPS 3130/6130 Computational Geometry Spring Voronoi Diagrams. Carola Wenk. Based on: Computational Geometry: Algorithms and Applications
 CMPS 3130/6130 Computational Geometry Spring 2015 Voronoi Diagrams Carola Wenk Based on: Computational Geometry: Algorithms and Applications 2/19/15 CMPS 3130/6130 Computational Geometry 1 Voronoi Diagram
CMPS 3130/6130 Computational Geometry Spring 2015 Voronoi Diagrams Carola Wenk Based on: Computational Geometry: Algorithms and Applications 2/19/15 CMPS 3130/6130 Computational Geometry 1 Voronoi Diagram
PS Computational Geometry Homework Assignment Sheet I (Due 16-March-2018)
 Homework Assignment Sheet I (Due 16-March-2018) Assignment 1 Let f, g : N R with f(n) := 8n + 4 and g(n) := 1 5 n log 2 n. Prove explicitly that f O(g) and f o(g). Assignment 2 How can you generalize the
Homework Assignment Sheet I (Due 16-March-2018) Assignment 1 Let f, g : N R with f(n) := 8n + 4 and g(n) := 1 5 n log 2 n. Prove explicitly that f O(g) and f o(g). Assignment 2 How can you generalize the
521493S Computer Graphics Exercise 3 (Chapters 6-8)
 521493S Comuter Grahics Exercise 3 (Chaters 6-8) 1 Most grahics systems and APIs use the simle lighting and reflection models that we introduced for olygon rendering Describe the ways in which each of
521493S Comuter Grahics Exercise 3 (Chaters 6-8) 1 Most grahics systems and APIs use the simle lighting and reflection models that we introduced for olygon rendering Describe the ways in which each of
Other Voronoi/Delaunay Structures
 Other Voronoi/Delaunay Structures Overview Alpha hulls (a subset of Delaunay graph) Extension of Voronoi Diagrams Convex Hull What is it good for? The bounding region of a point set Not so good for describing
Other Voronoi/Delaunay Structures Overview Alpha hulls (a subset of Delaunay graph) Extension of Voronoi Diagrams Convex Hull What is it good for? The bounding region of a point set Not so good for describing
Shuigeng Zhou. May 18, 2016 School of Computer Science Fudan University
 Query Processing Shuigeng Zhou May 18, 2016 School of Comuter Science Fudan University Overview Outline Measures of Query Cost Selection Oeration Sorting Join Oeration Other Oerations Evaluation of Exressions
Query Processing Shuigeng Zhou May 18, 2016 School of Comuter Science Fudan University Overview Outline Measures of Query Cost Selection Oeration Sorting Join Oeration Other Oerations Evaluation of Exressions
ON THE EMPTY CONVEX PARTITION OF A FINITE SET IN THE PLANE**
 Chin. Ann. of Math. 23B:(2002),87-9. ON THE EMPTY CONVEX PARTITION OF A FINITE SET IN THE PLANE** XU Changqing* DING Ren* Abstract The authors discuss the partition of a finite set of points in the plane
Chin. Ann. of Math. 23B:(2002),87-9. ON THE EMPTY CONVEX PARTITION OF A FINITE SET IN THE PLANE** XU Changqing* DING Ren* Abstract The authors discuss the partition of a finite set of points in the plane
Curve Reconstruction taken from [1]
![Curve Reconstruction taken from [1] Curve Reconstruction taken from [1]](/thumbs/95/124183256.jpg) Notes by Tamal K. Dey, OSU 47 Curve Reconstruction taken from [1] The simlest class of manifolds that ose nontrivial reconstruction roblems are curves in the lane. We will describe two algorithms for curve
Notes by Tamal K. Dey, OSU 47 Curve Reconstruction taken from [1] The simlest class of manifolds that ose nontrivial reconstruction roblems are curves in the lane. We will describe two algorithms for curve
Week 8 Voronoi Diagrams
 1 Week 8 Voronoi Diagrams 2 Voronoi Diagram Very important problem in Comp. Geo. Discussed back in 1850 by Dirichlet Published in a paper by Voronoi in 1908 3 Voronoi Diagram Fire observation towers: an
1 Week 8 Voronoi Diagrams 2 Voronoi Diagram Very important problem in Comp. Geo. Discussed back in 1850 by Dirichlet Published in a paper by Voronoi in 1908 3 Voronoi Diagram Fire observation towers: an
Optimal Compression of a Polyline with Segments and Arcs
 Optimal Compression of a Polyline with Segments and Arcs Alexander Gribov Esri 380 New York Street Redlands, CA 92373 Email: agribov@esri.com arxiv:1604.07476v5 [cs.cg] 10 Apr 2017 Abstract This paper
Optimal Compression of a Polyline with Segments and Arcs Alexander Gribov Esri 380 New York Street Redlands, CA 92373 Email: agribov@esri.com arxiv:1604.07476v5 [cs.cg] 10 Apr 2017 Abstract This paper
Computational Geometry Overview from Cormen, et al.
 UMass Lowell Computer Science 91.503 Graduate Algorithms Prof. Karen Daniels Spring, 2014 Computational Geometry Overview from Cormen, et al. Chapter 33 (with additional material from other sources) 1
UMass Lowell Computer Science 91.503 Graduate Algorithms Prof. Karen Daniels Spring, 2014 Computational Geometry Overview from Cormen, et al. Chapter 33 (with additional material from other sources) 1
6.854J / J Advanced Algorithms Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
Lecture 16: Voronoi Diagrams and Fortune s Algorithm
 contains q changes as a result of the ith insertion. Let P i denote this probability (where the probability is taken over random insertion orders, irrespective of the choice of q). Since q could fall through
contains q changes as a result of the ith insertion. Let P i denote this probability (where the probability is taken over random insertion orders, irrespective of the choice of q). Since q could fall through
Geometric Computation: Introduction
 : Introduction Piotr Indyk Welcome to 6.838! Overview and goals Course Information Syllabus 2D Convex hull Signup sheet Geometric computation occurs everywhere: Geographic Information Systems (GIS): nearest
: Introduction Piotr Indyk Welcome to 6.838! Overview and goals Course Information Syllabus 2D Convex hull Signup sheet Geometric computation occurs everywhere: Geographic Information Systems (GIS): nearest
The Edge-flipping Distance of Triangulations
 The Edge-fliing Distance of Triangulations Sabine Hanke (Institut für Informatik, Universität Freiburg, Germany hanke@informatik.uni-freiburg.de) Thomas Ottmann (Institut für Informatik, Universität Freiburg,
The Edge-fliing Distance of Triangulations Sabine Hanke (Institut für Informatik, Universität Freiburg, Germany hanke@informatik.uni-freiburg.de) Thomas Ottmann (Institut für Informatik, Universität Freiburg,
Geometric Dilation. A polygonal chain C. detour of C on the pair (p, q): where C q p the path on C connecting p and q. detour of C
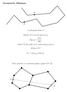 Geometric Dilation A olygonal chain C detour of C on the air (, ): δ(, ) = C, where C the ath on C connecting and. detour of C δ C = max, C δ(, ). More general: A connected lanar grah G(V, E) Gemetric
Geometric Dilation A olygonal chain C detour of C on the air (, ): δ(, ) = C, where C the ath on C connecting and. detour of C δ C = max, C δ(, ). More general: A connected lanar grah G(V, E) Gemetric
Voronoi diagrams Delaunay Triangulations. Pierre Alliez Inria
 Voronoi diagrams Delaunay Triangulations Pierre Alliez Inria Voronoi Diagram Voronoi Diagram Voronoi Diagram The collection of the non-empty Voronoi regions and their faces, together with their incidence
Voronoi diagrams Delaunay Triangulations Pierre Alliez Inria Voronoi Diagram Voronoi Diagram Voronoi Diagram The collection of the non-empty Voronoi regions and their faces, together with their incidence
CS 410/584, Algorithm Design & Analysis, Lecture Notes 8
 CS 410/584,, Computational Geometry Algorithms for manipulation of geometric objects We will concentrate on 2-D geometry Numerically robust try to avoid division Round-off error Divide-by-0 checks Techniques
CS 410/584,, Computational Geometry Algorithms for manipulation of geometric objects We will concentrate on 2-D geometry Numerically robust try to avoid division Round-off error Divide-by-0 checks Techniques
Dr Pavan Chakraborty IIIT-Allahabad
 GVC-43 Lecture - 5 Ref: Donald Hearn & M. Pauline Baker, Comuter Grahics Foley, van Dam, Feiner & Hughes, Comuter Grahics Princiles & Practice Dr Pavan Chakraborty IIIT-Allahabad Summary of line drawing
GVC-43 Lecture - 5 Ref: Donald Hearn & M. Pauline Baker, Comuter Grahics Foley, van Dam, Feiner & Hughes, Comuter Grahics Princiles & Practice Dr Pavan Chakraborty IIIT-Allahabad Summary of line drawing
Art Gallery, Triangulation, and Voronoi Regions
 Art Gallery, Triangulation, and Voronoi Regions CS535 Fall 2016 Daniel G. Aliaga Department of Computer Science Purdue University [some slides based on Profs. Shmuel Wimer and Andy Mirzaian Topics Triangulation
Art Gallery, Triangulation, and Voronoi Regions CS535 Fall 2016 Daniel G. Aliaga Department of Computer Science Purdue University [some slides based on Profs. Shmuel Wimer and Andy Mirzaian Topics Triangulation
Computational Geometry. HKU ACM ICPC Training 2010
 Computational Geometry HKU ACM ICPC Training 2010 1 What is Computational Geometry? Deals with geometrical structures Points, lines, line segments, vectors, planes, etc. A relatively boring class of problems
Computational Geometry HKU ACM ICPC Training 2010 1 What is Computational Geometry? Deals with geometrical structures Points, lines, line segments, vectors, planes, etc. A relatively boring class of problems
5. DIVIDE AND CONQUER I
 5. DIVIDE AND CONQUER I mergesort counting inversions closest pair of points randomized quicksort median and selection Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 2013
5. DIVIDE AND CONQUER I mergesort counting inversions closest pair of points randomized quicksort median and selection Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 2013
CSE 421 Closest Pair of Points, Master Theorem, Integer Multiplication
 CSE 421 Closest Pair of Points, Master Theorem, Integer Multiplication Shayan Oveis Gharan 1 Finding the Closest Pair of Points Closest Pair of Points (non geometric) Given n points and arbitrary distances
CSE 421 Closest Pair of Points, Master Theorem, Integer Multiplication Shayan Oveis Gharan 1 Finding the Closest Pair of Points Closest Pair of Points (non geometric) Given n points and arbitrary distances
Computational Geometry
 Computational Geometry Range queries Convex hulls Lower bounds Planar subdivision search Line segment intersection Convex polygons Voronoi diagrams Minimum spanning trees Nearest neighbors Triangulations
Computational Geometry Range queries Convex hulls Lower bounds Planar subdivision search Line segment intersection Convex polygons Voronoi diagrams Minimum spanning trees Nearest neighbors Triangulations
Range Searching. Data structure for a set of objects (points, rectangles, polygons) for efficient range queries.
 Range Searching Data structure for a set of objects (oints, rectangles, olygons) for efficient range queries. Y Q Deends on tye of objects and queries. Consider basic data structures with broad alicability.
Range Searching Data structure for a set of objects (oints, rectangles, olygons) for efficient range queries. Y Q Deends on tye of objects and queries. Consider basic data structures with broad alicability.
Connected Components of Underlying Graphs of Halving Lines
 arxiv:1304.5658v1 [math.co] 20 Apr 2013 Connected Components of Underlying Graphs of Halving Lines Tanya Khovanova MIT November 5, 2018 Abstract Dai Yang MIT In this paper we discuss the connected components
arxiv:1304.5658v1 [math.co] 20 Apr 2013 Connected Components of Underlying Graphs of Halving Lines Tanya Khovanova MIT November 5, 2018 Abstract Dai Yang MIT In this paper we discuss the connected components
Computational Geometry Algorithmische Geometrie
 Algorithmische Geometrie Panos Giannopoulos Wolfgang Mulzer Lena Schlipf AG TI SS 2013 !! Register in Campus Management!! Outline What you need to know (before taking this course) What is the course about?
Algorithmische Geometrie Panos Giannopoulos Wolfgang Mulzer Lena Schlipf AG TI SS 2013 !! Register in Campus Management!! Outline What you need to know (before taking this course) What is the course about?
1 Definition of Reduction
 1 Definition of Reduction Problem A is reducible, or more technically Turing reducible, to problem B, denoted A B if there a main program M to solve problem A that lacks only a procedure to solve problem
1 Definition of Reduction Problem A is reducible, or more technically Turing reducible, to problem B, denoted A B if there a main program M to solve problem A that lacks only a procedure to solve problem
3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College
![3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College 3D convex hulls. Computational Geometry [csci 3250] Laura Toma Bowdoin College](/thumbs/90/102029124.jpg) 3D convex hulls Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hulls The problem: Given a set P of points, compute their convex hull 2D 3D 2D 3D polygon polyhedron Polyhedron region
3D convex hulls Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hulls The problem: Given a set P of points, compute their convex hull 2D 3D 2D 3D polygon polyhedron Polyhedron region
Computational Geometry
 Lecture 12: Lecture 12: Motivation: Terrains by interpolation To build a model of the terrain surface, we can start with a number of sample points where we know the height. Lecture 12: Motivation: Terrains
Lecture 12: Lecture 12: Motivation: Terrains by interpolation To build a model of the terrain surface, we can start with a number of sample points where we know the height. Lecture 12: Motivation: Terrains
Constrained Empty-Rectangle Delaunay Graphs
 CCCG 2015, Kingston, Ontario, August 10 12, 2015 Constrained Emty-Rectangle Delaunay Grahs Prosenjit Bose Jean-Lou De Carufel André van Renssen Abstract Given an arbitrary convex shae C, a set P of oints
CCCG 2015, Kingston, Ontario, August 10 12, 2015 Constrained Emty-Rectangle Delaunay Grahs Prosenjit Bose Jean-Lou De Carufel André van Renssen Abstract Given an arbitrary convex shae C, a set P of oints
Ma/CS 6b Class 26: Art Galleries and Politicians
 Ma/CS 6b Class 26: Art Galleries and Politicians By Adam Sheffer The Art Gallery Problem Problem. We wish to place security cameras at a gallery, such that they cover it completely. Every camera can cover
Ma/CS 6b Class 26: Art Galleries and Politicians By Adam Sheffer The Art Gallery Problem Problem. We wish to place security cameras at a gallery, such that they cover it completely. Every camera can cover
Clipping. Administrative. Assignment 1 Gallery. Questions about previous lectures? Overview of graphics pipeline? Assignment 2
 Cliing MIT EECS 6.837 Frédo Durand and Seth Teller Some slides and images courtesy of Leonard McMillan MIT EECS 6.837, Teller and Durand 1 MIT EECS 6.837, Teller and Durand 2 Administrative Assignment
Cliing MIT EECS 6.837 Frédo Durand and Seth Teller Some slides and images courtesy of Leonard McMillan MIT EECS 6.837, Teller and Durand 1 MIT EECS 6.837, Teller and Durand 2 Administrative Assignment
CS335 Fall 2007 Graphics and Multimedia. 2D Drawings: Lines
 CS335 Fall 007 Grahics and Multimedia D Drawings: Lines Primitive Drawing Oerations Digital Concets of Drawing in Raster Arras PIXEL is a single arra element at x, - No smaller drawing unit exists Px,
CS335 Fall 007 Grahics and Multimedia D Drawings: Lines Primitive Drawing Oerations Digital Concets of Drawing in Raster Arras PIXEL is a single arra element at x, - No smaller drawing unit exists Px,
The Spatial Skyline Queries
 Coffee sho The Satial Skyline Queries Mehdi Sharifzadeh and Cyrus Shahabi VLDB 006 Presented by Ali Khodaei Coffee sho Three friends Coffee sho Three friends Don t choose this lace is closer to each three
Coffee sho The Satial Skyline Queries Mehdi Sharifzadeh and Cyrus Shahabi VLDB 006 Presented by Ali Khodaei Coffee sho Three friends Coffee sho Three friends Don t choose this lace is closer to each three
UPDATING ALGORITHMS FOR CONSTRAINT DELAUNAY TIN
 UPDATING ALGORITMS FOR CONSTRAINT DELAUNAY TIN WU LiXin a,b WANG YanBing a, c a Institute for GIS/RS/GPS & Subsidence Engineering Research, China Uni Mining & Technology, Beijing, China, 100083 - awulixin@263.net,
UPDATING ALGORITMS FOR CONSTRAINT DELAUNAY TIN WU LiXin a,b WANG YanBing a, c a Institute for GIS/RS/GPS & Subsidence Engineering Research, China Uni Mining & Technology, Beijing, China, 100083 - awulixin@263.net,
Math 414 Lecture 2 Everyone have a laptop?
 Math 44 Lecture 2 Everyone have a laptop? THEOREM. Let v,...,v k be k vectors in an n-dimensional space and A = [v ;...; v k ] v,..., v k independent v,..., v k span the space v,..., v k a basis v,...,
Math 44 Lecture 2 Everyone have a laptop? THEOREM. Let v,...,v k be k vectors in an n-dimensional space and A = [v ;...; v k ] v,..., v k independent v,..., v k span the space v,..., v k a basis v,...,
Notes and Answers to Homework Exam 1, Geometric Algorithms, 2017
 Notes and Answers to Homework Exam 1, Geometric Algorithms, 2017 Below are some notes and sketches of correct answers for the first homework exam. We have also included the most common mistakes that were
Notes and Answers to Homework Exam 1, Geometric Algorithms, 2017 Below are some notes and sketches of correct answers for the first homework exam. We have also included the most common mistakes that were
Advanced Algorithms Computational Geometry Prof. Karen Daniels. Spring, 2010
 UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Spring, 2010 Lecture 3 O Rourke Chapter 3: 2D Convex Hulls Thursday, 2/18/10 Chapter 3 2D Convex Hulls
UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Spring, 2010 Lecture 3 O Rourke Chapter 3: 2D Convex Hulls Thursday, 2/18/10 Chapter 3 2D Convex Hulls
Discrete Mathematics I So Practice Sheet Solutions 1
 Discrete Mathematics I So 2016 Tibor Szabó Shagnik Das Practice Sheet Solutions 1 Provided below are possible solutions to the questions from the practice sheet issued towards the end of the course. Exercise
Discrete Mathematics I So 2016 Tibor Szabó Shagnik Das Practice Sheet Solutions 1 Provided below are possible solutions to the questions from the practice sheet issued towards the end of the course. Exercise
CS 410/584, Algorithm Design & Analysis, Lecture Notes 8!
 CS 410/584, Algorithm Design & Analysis, Computational Geometry! Algorithms for manipulation of geometric objects We will concentrate on 2-D geometry Numerically robust try to avoid division Round-off
CS 410/584, Algorithm Design & Analysis, Computational Geometry! Algorithms for manipulation of geometric objects We will concentrate on 2-D geometry Numerically robust try to avoid division Round-off
Tutte s Theorem: How to draw a graph
 Spectral Graph Theory Lecture 15 Tutte s Theorem: How to draw a graph Daniel A. Spielman October 22, 2018 15.1 Overview We prove Tutte s theorem [Tut63], which shows how to use spring embeddings to obtain
Spectral Graph Theory Lecture 15 Tutte s Theorem: How to draw a graph Daniel A. Spielman October 22, 2018 15.1 Overview We prove Tutte s theorem [Tut63], which shows how to use spring embeddings to obtain
CMSC 754 Computational Geometry 1
 CMSC 754 Computational Geometry 1 David M. Mount Department of Computer Science University of Maryland Fall 2005 1 Copyright, David M. Mount, 2005, Dept. of Computer Science, University of Maryland, College
CMSC 754 Computational Geometry 1 David M. Mount Department of Computer Science University of Maryland Fall 2005 1 Copyright, David M. Mount, 2005, Dept. of Computer Science, University of Maryland, College
Chapter 3: Graphics Output Primitives. OpenGL Line Functions. OpenGL Point Functions. Line Drawing Algorithms
 Chater : Grahics Outut Primitives Primitives: functions in grahics acage that we use to describe icture element Points and straight lines are the simlest rimitives Some acages include circles, conic sections,
Chater : Grahics Outut Primitives Primitives: functions in grahics acage that we use to describe icture element Points and straight lines are the simlest rimitives Some acages include circles, conic sections,
Delaunay Triangulations
 Delaunay Triangulations (slides mostly by Glenn Eguchi) Motivation: Terrains Set of data points A R 2 Height ƒ(p) defined at each point p in A How can we most naturally approximate height of points not
Delaunay Triangulations (slides mostly by Glenn Eguchi) Motivation: Terrains Set of data points A R 2 Height ƒ(p) defined at each point p in A How can we most naturally approximate height of points not
A Minimalist s Implementation of the 3-d Divide-and-Conquer Convex Hull Algorithm
 A Minimalist s Implementation of the 3-d Divide-and-Conquer Convex Hull Algorithm Timothy M. Chan Presented by Dana K. Jansens Carleton University Simple Polygons Polygon = A consecutive set of vertices
A Minimalist s Implementation of the 3-d Divide-and-Conquer Convex Hull Algorithm Timothy M. Chan Presented by Dana K. Jansens Carleton University Simple Polygons Polygon = A consecutive set of vertices
5.4 Closest Pair of Points
 5.4 Closest Pair of Points Closest pair. Given n points in the plane, find a pair with smallest Euclidean distance between them. Fundamental geometric primitive. Graphics, computer vision, geographic information
5.4 Closest Pair of Points Closest pair. Given n points in the plane, find a pair with smallest Euclidean distance between them. Fundamental geometric primitive. Graphics, computer vision, geographic information
Midpoint Routing algorithms for Delaunay Triangulations
 Midpoint Routing algorithms for Delaunay Triangulations Weisheng Si and Albert Y. Zomaya Centre for Distributed and High Performance Computing School of Information Technologies Prologue The practical
Midpoint Routing algorithms for Delaunay Triangulations Weisheng Si and Albert Y. Zomaya Centre for Distributed and High Performance Computing School of Information Technologies Prologue The practical
Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College
![Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College](/thumbs/86/93358306.jpg) Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull Given a set P of points in 2D, their convex hull is the smallest convex polygon that contains all points
Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull Given a set P of points in 2D, their convex hull is the smallest convex polygon that contains all points
Prof. Gill Barequet. Center for Graphics and Geometric Computing, Technion. Dept. of Computer Science The Technion Haifa, Israel
 Computational Geometry (CS 236719) http://www.cs.tufts.edu/~barequet/teaching/cg Chapter 1 Introduction 1 Copyright 2002-2009 2009 Prof. Gill Barequet Center for Graphics and Geometric Computing Dept.
Computational Geometry (CS 236719) http://www.cs.tufts.edu/~barequet/teaching/cg Chapter 1 Introduction 1 Copyright 2002-2009 2009 Prof. Gill Barequet Center for Graphics and Geometric Computing Dept.
Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here)
 Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here) Voronoi Diagram & Delaunay Triangualtion Algorithms Divide-&-Conquer Plane Sweep Lifting
Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here) Voronoi Diagram & Delaunay Triangualtion Algorithms Divide-&-Conquer Plane Sweep Lifting
Figure 2.1: An example of a convex set and a nonconvex one.
 Convex Hulls 2.1 Definitions 2 Convexity is the key to understanding and simplifying geometry, and the convex hull plays a role in geometry akin to the sorted order for a collection of numbers. So what
Convex Hulls 2.1 Definitions 2 Convexity is the key to understanding and simplifying geometry, and the convex hull plays a role in geometry akin to the sorted order for a collection of numbers. So what
KD-Tree Algorithm for Propensity Score Matching PhD Qualifying Exam Defense
 KD-Tree Algorithm for Propensity Score Matching PhD Qualifying Exam Defense John R Hott University of Virginia May 11, 2012 1 / 62 Motivation Epidemiology: Clinical Trials Phase II and III pre-market trials
KD-Tree Algorithm for Propensity Score Matching PhD Qualifying Exam Defense John R Hott University of Virginia May 11, 2012 1 / 62 Motivation Epidemiology: Clinical Trials Phase II and III pre-market trials
COMPUTING CONSTRAINED DELAUNAY
 COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE By Samuel Peterson, University of Minnesota Undergraduate The Goal The Problem The Algorithms The Implementation Applications Acknowledgments
COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE By Samuel Peterson, University of Minnesota Undergraduate The Goal The Problem The Algorithms The Implementation Applications Acknowledgments
CS3110 Spring 2017 Lecture 14: Computational Geometry and Convex Hulls
 CS3110 Spring 2017 Lecture 14: Computational Geometry and Convex Hulls Robert Constable 1 Lecture Plan 1. Cantor s Theorem, as stated by Bishop [1]. 2. Background for geometry 3. Finding the convex hull
CS3110 Spring 2017 Lecture 14: Computational Geometry and Convex Hulls Robert Constable 1 Lecture Plan 1. Cantor s Theorem, as stated by Bishop [1]. 2. Background for geometry 3. Finding the convex hull
Introduction to Visualization and Computer Graphics
 Introduction to Visualization and Comuter Grahics DH2320, Fall 2015 Prof. Dr. Tino Weinkauf Introduction to Visualization and Comuter Grahics Grids and Interolation Next Tuesday No lecture next Tuesday!
Introduction to Visualization and Comuter Grahics DH2320, Fall 2015 Prof. Dr. Tino Weinkauf Introduction to Visualization and Comuter Grahics Grids and Interolation Next Tuesday No lecture next Tuesday!
Polygon Triangulation
 Polygon Triangulation The problem: Triangulate a given polygon. (output a set of diagonals that partition the polygon into triangles). Computational Geometry [csci 3250] Polygon Triangulation Laura Toma
Polygon Triangulation The problem: Triangulate a given polygon. (output a set of diagonals that partition the polygon into triangles). Computational Geometry [csci 3250] Polygon Triangulation Laura Toma
26 The closest pair problem
 The closest pair problem 1 26 The closest pair problem Sweep algorithms solve many kinds of proximity problems efficiently. We present a simple sweep that solves the two-dimensional closest pair problem
The closest pair problem 1 26 The closest pair problem Sweep algorithms solve many kinds of proximity problems efficiently. We present a simple sweep that solves the two-dimensional closest pair problem
