We will then introduce the DT, discuss some of its fundamental properties and show how to compute a DT directly from a given set of points.

Transcription

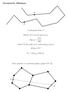
1 Voronoi Diagram and Delaunay Triangulation 1 Introduction The Voronoi Diagram (VD, for short) is a ubiquitious structure that aears in a variety of discilines - biology, geograhy, ecology, crystallograhy, to mention just a few. The VD and its dual, the Delaunay Triangulation (DT, fot short), are two of the most imortant and fundamental data structures in Comutational Geometry that have been succesfully alied to a variety of roximity roblems. We will study a few of these later. It is not surrising therefore that these have received a lot of attention from researchers, leading to a very extensive literarure on their roerties and alications. In this chater we will first describe what is a VD and discuss some of its basic roerties. Next we will discuss algorithms for comuting the VD and exlore some of its alications in solving other Comutational Geometry roblems. We will then introduce the DT, discuss some of its fundamental roerties and show how to comute a DT directly from a given set of oints. 2 Voronoi diagrams Three ingredients are needed to define a VD: a set of objects, an ambient sace in which these objects are embedded and a notion of distance between a oint of the ambient sace and a subset of the given set of objects. The distance function enables us to define bisectors of airs of sets of objects that artition the ambient sace into a VD of the given set of objects. Here s a concrete and simle examle. Let the set of objects be a set S of n sites (oints) {s 1,s 2,...,s n }, the ambient sace the two dimensional lane and the distance be the Euclidean distance between any oint of the lane and a site in S. The bisectors between airs of sites are straight lines that artition the lane into n convex regions, one corresonding to each site s i. The region of site s i is called the Voronoi olygon of s i and consists of the oints which are closer to site s i than to the remaining sites in S. The resulting artition of the lane is called a (nearest oint) VD of S. Figure 1 below shows a Voronoi diagram on 4 sites. The vertices and edges that make u the boundaries of the convex regions are called Voronoi edges and Voronoi vertices resectively. As is obvious, by varying the three ingredients we mentioned above we get a wide variety of Voronoi diagrams (see [2] for the amazing variety of ossibilities). While in this chater we will be mainly 1

2 s 1 s 2 s 4 s 3 Figure 1: Voronoi diagram of 4 oints concerned with Voronoi diagrams of a set of oint sites, we will mention a few of the more wellstudied ones at the end of the chater. 3 Proerties of a nearest oint Voronoi Diagram We establish a few useful roerties of this diagram, assuming that no four oints are co-circular (that is, lie on the same circle). Claim 1 The number of Voronoi vertices and edges are resectively 2(n 1) h and 3(n 1) h resectively, where n is the number of sites and h the number of sites on the convex hull of S. A finite grah satsfies Euler s formula V E + F = 2 for a convex olyhedron, where V, E and F are resectively the number of vertices, edges and faces of the olyhedron (grah). This can be established by a stereograhic rojection of the olyhedron, embedded on the surface of a shere, into a finite grah. The Voronoi diagram of a set of n sites can be transformed into a finite grah by enclosing the Voronoi diagram inside a very large circle and treating each of the h (= # of convex hull vertices of the given oint set) arcs that lie inside an unbounded Voronoi olygon to corresond to an edge of the grah. For this finite grah, we use the fact that 2E = 3V (each side of the equality counts the total degree of the grah) to deduce, using Euler s formula, that V = 2(F 2) and E = 3(F 2). Now V = h + # V oronoi vertices and E = h + # V oronoi edges. Hence the number of Voronoi vertices = 2(F 2) h and the number of Voronoi edges = 3(F 2) h. Since F = n + 1, these counts are therefore 2(n 1) h and 3(n 1) h resectively. Claim 2 Every Voronoi vertex is of degree 3. 2

3 Proof: Otherwise, 4 or more oints would be co-circular, contrary to our assumtion. The next roerty is significant. Claim 3 The circle C(v), centered at a Voronoi vertex v, and assing through the sites that define v has no other sites in its interior. Proof: By the definition of v it is closest to the sites that define it; a site in the interior of C(v) by being closer to v would contradict this definition. (see Fig 2). s 1 v s 3 s 2 Figure 2: No sites in the interior of C(v) Another interesting question is this: which bisectors define the edges of the Voronoi olygon of a site s i? Claim 4 The bisector of the sites s i and defines an edge of the Voronoi olygon of s i (and thus symmetrically that of the Voronoi olygon of ) iff there exists a oint of the lane whose nearest sites are both s i and simultaneously. Proof: (only if) Let the site contribute an edge to the Voronoi olygon of s i. Let be an internal oint on this edge. If s i and are not the nearest sites of, let s k be a site that is closer. From Fig. 3 it is clear that this redefines the edge that contributes to the Voronoi olygon of s i to exclude. This contradicts the assumtion that is an internal oint of the edge of the Voronoi olygon of s i due to. Thus cannot have a site closer to it than s i and. (if) Let there exist a oint whose nearest sites are both s i and. Thus must lie on the bisector of s i and. If we move slightly along towards, then becomes the closest site of, utting it in the Voronoi olygon of ; in the same way, by moving it along s i towards s i, we ut it in the Voronoi olygon of s i. Thus must belong to the art of the bisector of s i and that is a common edge of their Voronoi olygons. The next claim shows a nice connection beween the VD of a set of oints and its convex hull. 3

4 s k s i Figure 3: When is closer to s k than s i or... Claim 5 The Voronoi olygon of s i is unbounded iff s i is a oint on the boundary of the convex hull of S. Proof: (only if) Let s i be a site interior to the convex hull of S. This imlies that s i lies inside the triangle formed by some trilet of sites on the hull boundary. The bounded region formed by the bisectors of s i and each of these three sites contains the Voronoi olygon of s i. Hence the Voronoi olygon of s i is bounded. (if) Let s i be a site on the hull boundary of S. Let and s k be sites adjacent to it on the hull boundary. Consider a suorting line l of the convex hull through s i. Let be a oint on a ray through s i that is orthogonal to l and C() be a circle centered at with radius s i (see Fig. 4). The oint is in the Voronoi olygon of s i, since by construction any other site is farther from it than the radius of C(). Since is an arbitrary oint on the line orthogonal to l, the Voronoi olygon of s i is unbounded. The dual of the Voronoi diagram is obtained by joining airs of sites whose Voronoi olygons are adjacent. We next show that: Claim 6 The dual of the Voronoi diagram of S is a triangulation 1 of S. Proof: We first show that no two segments in the dual diagram intersect excet at their end oints. Assume that the segmentoining the sites s i and intersect the segment joining the sites s u and s v at the oint. If is the mid-oint of both segments then would have to belong to the Voronoi olygons of the sites s i,, s u and s v. This is imossible as a oint can belong to at most three different Voronoi 1 Given n oints in the lane, join them by nonintersecting straight line segments so that every region internal to the convex hull is a triangle. 4

5 r C() s i s k Figure 4: A convex hull vertex of S has an unbounded Voronoi olygon olygons. Thus lies on one side of the mid-oint of at least one of the two segments, say s i. If is the mid-oint of the other segement, then is on the boundary of the Voronoi olygons of s u and s v, and in the interior of the Voronoi diagram of s i as well. This is not ossible. Otherwise is closer to, say s u, than s v. Hence is in the interior of the Voronoi olygons of s i as well as s v (see Fig. 5). This is also imossible. Thus in all cases we conclude that the segments s i and s u s v cannot cross. s u s i s u s u s v s i s v s i (a) (b) (c) s v Figure 5: Non-intersection of two segments in the dual diagram Next, we show that the set of segments in the dual diagram is maximal. 5

6 Suose otherwise. This imlies we can add a segment joining two sites s i and whose Voronoi diagrams are non-adjacent, while still satisfying the non-intersection roerty. Thus the set of edgeoining airs of sites due to the dualization form a maximal set. This triangulation is the famous Delaunay triangulation on S. 4 Constructing a Voronoi diagram Many algorithms are available for constructing a (nearest oint) Voronoi diagram. An algorithm based on the divide-and-conquer aradigm is described in the textbook by Prearata and Shamos [1]. This algorithm is messy and hard to understand. Here we will describe a simle and beautiful algorithm by Fortune [] that is based on the sweeline aradigm. The surrising asect of this algorithm is the alicability of the sweeline technique to this roblem - something that aears imossible at first sight. Here, we will indulge in a brief digression to exlain the sweeline technique so that the cleverness of Fortune s algorithm is better areciated. The sweeline technique as the very name suggests is a method by which we swee a line through a set of geometric objects from left to right (or right to left, if you wish) in order to comute some function on these objects. For examle, given a set of line segments in the lane (again!) we might be interested in determining all airs of segments that intersect or, maybe, just obtain a count of the number of interesecting airs. This can be accomlished with two simle data structures - a sweeline structure that kees track of all the line segments that intersect the current osition of the sweeline and an event queue that kees track of the discrete set of events where the sweeline structure changes (for more details see Prearata and Shamos [1]). The significant fact for us to notice is that an individual segment aears in the sweeline structure at the event corresonding to its left end-oint and disaears from the sweeline at the event corresonding to its right end-oint. All the intersections due to this segment are discovered beween these two events, so that once this segment leaves the sweeline status no new intersections due to this segment remain to be discovered. If we try to aly this technique in a straightforward way to comuting the Voronoi digram of a set of oints we immediately encounter the roblem that the Voronoi olygon of a oint (this is an event) extends on both sides of this event. In other words, the comutation of the Voronoi olygon of a oint is not comlete when the sweeline goes ast the oint. Fortune roosed a novel way of getting around this difficulty. In addition to the usual sweeline infrastructure, the effect of a oint-event is maintained in the form of a arabola that is generated when the sweeline reaches a oint. This arabola has the oint as its focus and the sweeline as 6

7 its directrix so that it trails the sweeline. and remains active till the Voronoi olygon of the oint that caused its generation has been constructed. All active arabolas are maintained as a beach-front made u of arabolic arcs (in mathematical terms, this is is an uer enveloe of all the active arabolas) that changes dynamically as new arabolas are added and inactive arabolas are removed. An intriguing question that cros u is how does a arabola best reresent the interest of an event oint. To answer this question we note that the Voronoi edges are generated by the intersection of a air of arabolas that are adjacent on the beach line. A Voronoi vertex is generated when three arabolas on the beach-front meet at a oint. This oint is equidistant from the oints that are the foci of these three arabolas as well as from the sweeline which is the directrix of all three. The circle centered at this common intersection oint, with radius equal to distance from the directrix is tangent to the directrix, assing through the foci af all the three arabolas, and is thus called a tangent-event. At this time, a Voronoi vertex is generated and the middle of the three arabolas disaears from the beach-front. 5 Delaunay Triangulation As exlained earlier, the dual of the Voronoi diagram of S is a (the?) Delaunay Triangulation (DT, for short from now on) on S, and as such it is a byroduct of the Voronoi diagram construction algorithm. However, it is ossible to construct a DT directly from the given set of oints S. Below, we discuss such an algorithm based on the incremental construction aradigm. A Delaunay triangulation on S is (uniquely?) characterized by the roerty that the circumcircle of each triangle contains no other sites in its interior. This folllows from the emty circle roerty of a Voronoi diagram described in the revious section. In the algorithm below, we will need the following characterization of an edge in the DT. Claim 7 An edge connecting two sites s i and is an edge in the DT iff there exists a circle assing through s i and that does not contain any site in its interior. 5.1 Incremental Algorithm Assume that we have constructed the DT of the first i 1 sites (i > 3), DT i 1. To udate this triangulation uon addition of the oint i, we first locate the triangle rst of DT i 1 in which i lies. Then the edges i r, i s and i s are new Delaunay triangulation edges (Claim 7). We show, for examle, that i r is a Delaunay edge. Let rr be a diameter of the circle circumscribing triangle rst (see Fig. 6). Choose r on this diameter so that i r and i r are orthogonal. The circle on rr as diameter goes through the edge i r, and has no site in its interior because it is entirely inside the circumcircle of rst. 7

8 r t i r s r Figure 6: New Delaunay edges incident on i A triangle T in the current triangulation is said to be in conflict with i if the circumcircle of triangle T contains i and thus cannot be art of DT i. Thus the status of the edges rs, st and tr need to be checked. Consider the edge rs, and the triangle rs, not containing i. If triangle rs is in conflict with i then the edge rs is not a Delaunay edge and we relace it by the new edge i. This is called edge-fliing. Every time we do an edge-fliing two new edges are u for the circumcircle test. We continue till no edge-fliing occurs, when we have the Delaunay triangulation of the i sites Analysis of the Incremental Algorithm The following gross analysis tells us that the algorithm is in O(n 2 ). The number of edge-fliings caused by the insertion of i is roortional to the degree of this vertex in the triangulation. The degree of each vertex is in O(i) and hence the total number of edge-fliings after the insertion of the n-th oint is in O(n 2 ). The cost of a brute-force location of the oint i in DT i 1 is also in O(i) and hence the cost over the entire sequence of n insertions is in O(n 2 ). A more subtle (and messy!) analysis shows that the exected comlexity of this algorithm is in O(n log n). The first observation is that the average degree of a site in the DT is at most 6, since there are at most 3n 6 edges. Thus if we make a random sequence of insertions the exected number of edge-fliings is in O(n). 5.2 The Delaunay Tree Data Structure The Delaunay Tree data structure rovides a more efficient alternative to the brute-force search for finding a triangle in DT i 1 that contains i. It is a layered DAG (short for Directed Acyclic 8

9 Grah) in which we maintain all triangles created during the incremental construction. The i-th layer consists of traingles created during insertion of site i. The root (0-th layer) of this Delaunay tree is a large triangle that contains all the sites of S. From each each node (storing a triangle) at a given layer, we maintain ointers to all nodes in the next layer that store triangles that overla with this triangle. Referring to the discussion above, we thus kee ointers from the nodes that stores the old triangles rst and rs to the triangle i s if it is in DT i. To locate i in the DAG corresonding to DT i 1, we start at the root of the DAG and follow the ointers to descend along a ath in which the triangles are in conflict with i till we hit a leaf node which stores the triangle that contains i. We first rove the following claims. Claim 8 If the triangle of DT i 1 containing i is known, the structural work needed for comuting DT i from DT i 1 is roortional to the degree of i in DT i. Claim 9 For each h < i, let d h denote the exected number of triangles in DT h \ DT h 1 that are in conflict with i, then i h=1 d h = O(log i) Proof: Let C denote the set of triangles in DT h that are in conflict with i. A triangle T C belongs to DT h \ DT h 1 iff it has h as a vertex. Since the number of triangles in DT h is 2 h 5 and the exected degree of h is 6 the robability that a triangle in conflict with i survives is 6/(2 h 5) = 3/h, under the assumtion that h is randomly chosen. Thus, the exected number of triangles in C\ DT h 1 is 3 (C) /h. Since the exected size of C is less than 6(because the average degree of i is at most 6), therefore d h < 18/h. Thus, i h=1 d h = O(log i). It follows from the last lemma that the exected comlexity of the incremental construction algorithm is in O(n log n). References [1] F.Prearata and M.I. Shamos. Comutational Geometry: An Introduction, Sringer Verlag [2] A. Okabe, B. Boots and K. Sugihara. Satial Tessellations: Concets and Alications of Voronoi Diagrams, John Wiley, 2nd edition, [3] F. Aurenhammer. Voronoi Diagrams: A survey of a fundamental geometric data structure, ACM Comuting Surveys, 23(3): , Set