Graphs. Shortest Path and Topological Sort
|
|
|
- Gwendoline Snow
- 5 years ago
- Views:
Transcription
1 Graphs Shortest Path ad Topological Sort
2 Example Relatioal Networks School Friedship Network (from Moody 2001) Yeast Metabolic Network (from Terrorist Network (by Valdis Krebs, Orget.com) Protei-Protei Iteractios (by Peter Uetz) 2
3 More Relatioal Networks Flickr Social Network (from gustavog/sets/164006/) Campaig Cotributios from Oil Compaies (from Geomic Associatios (from Sel et al., 2002) Seagrass Food Web (geerated at 3
4 Basic Graph Defiitios A graph G = (V,E) cosists of a fiite set of vertices, V, ad a fiite set of edges, E. Each edge is a pair (v,w) where v, w Î V. q V ad E are sets, so each vertex v Î V is uique, ad each edge e Î E is uique. q Edges are sometimes called arcs or lies. q Vertices are sometimes called odes or poits. 4
5 Graph Applicatios Graphs ca be used to model a wide rage of applicatios icludig Itersectios ad streets withi a city Roads/trais/airlie routes coectig cities/coutries Computer etworks Electroic circuits 5
6 Basic Graph Defiitios (2) A directed graph is a graph i which the edges are ordered pairs. That is, (u,v) ¹ (v,u), u, v Î V. Directed graphs are sometimes called digraphs. A udirected graph is a graph i which the edges are uordered pairs. That is, (u,v) = (v,u). A sparse graph is oe with few edges. That is E = O( V ) A dese graph is oe with may edges. That is E = O( V 2 ) 6
7 Udirected Graph All edges are two-way. Edges are uordered pairs. V = { 1, 2,3, 4, 5} 3 4 E = { (1,2), (2, 3), (3, 4), (2, 4), (4, 5), (5, 1) } 7
8 Directed Graph All edges are oe-way as idicated by the arrows. Edges are ordered pairs. V = { 1, 2, 3, 4, 5} E = { (1, 2), (2, 4), (3, 2), (4, 3), (4, 5), (5, 4), (5, 1) } 8
9 A Sigle Graph with Multiple Compoets
10 Basic Graph Defiitios (3) Vertex w is adjacet to vertex v if ad oly if (v, w) Î E. For udirected graphs, with edge (v, w), ad hece also (w, v), w is adjacet to v ad v is adjacet to w. A edge may also have: q weight or cost -- a associated value q label -- a uique ame The degree of a vertex, v, is the umber of vertices adjacet to v. Degree is also called valece. 10
11 Basic Graph Defiitios (4) For directed graphs vertex w is adjacet to vertex v if ad oly if (v, w) Î E. Idegree of a vertex w is the umber of edges (v,w). OutDegree of a vertex w is the umber of edges(w,v)
12 Paths i Graphs A path i a graph is a sequece of vertices w 1, w 2, w 3,, w such that (w i, w i+1 ) Î E for 1 i <. The legth of a path i a graph is the umber of edges o the path. The legth of the path from a vertex to itself is 0. A simple path is a path such that all vertices are distict, except that the first ad last may be the same. A cycle i a graph is a path w 1, w 2, w 3,, w, w Î V such that: q q q there are at least two vertices o the path w 1 = w (the path starts ad eds o the same vertex) if ay part of the path cotais the subpath w i, w j, w i, the each of the edges i the subpath is distict (i. e., o backtrackig alog the same edge) A simple cycle is oe i which the path is simple. A directed graph with o cycles is called a directed acyclic graph, ofte abbreviated as DAG 12
13 Paths i Graphs (2) How may simple paths from 1 to 4 ad what are their legths?
14 Coectedess i Graphs A udirected graph is coected if there is a path from every vertex to every other vertex. A directed graph is strogly coected if there is a path from every vertex to every other vertex. A directed graph is weakly coected if there would be a path from every vertex to every other vertex, disregardig the directio of the edges. A complete graph is oe i which there is a edge betwee every pair of vertices. A coected compoet of a graph is ay maximal coected subgraph. Coected compoets are sometimes simply called compoets. 14
15 Disjoit Sets ad Graphs Disjoit sets ca be used to determie coected compoets of a udirected graph. For each edge, place its two vertices (u ad v) i the same set -- i.e. uio( u, v ) Whe all edges have bee examied, the forest of sets will represet the coected compoets. Two vertices, x, y, are coected if ad oly if fid( x ) = fid( y ) 15
16 Udirected Graph/Disjoit Set Example Sets represetig coected compoets { 1, 2, 3, 4, 5 } { 6 } { 7, 8, 9 } 9 16
17 DiGraph / Strogly Coected Compoets a b g d c f h e j i 17
18 A Graph ADT Has some data elemets q Vertices ad Edges Has some operatios q q q getdegree( u ) -- Returs the degree of vertex u (outdegree of vertex u i directed graph) getadjacet( u ) -- Returs a list of the vertices adjacet to vertex u (list of vertices that u poits to for a directed graph) isadjacetto( u, v ) -- Returs TRUE if vertex v is adjacet to vertex u, FALSE otherwise. Has some associated algorithms to be discussed. 18
19 Adjacecy Matrix Implemetatio Uses array of size V V where each etry (i,j) is boolea q q q TRUE if there is a edge from vertex i to vertex j FALSE otherwise store weights whe edges are weighted Very simple, but large space requiremet = O( V 2 ) Appropriate if the graph is dese. Otherwise, most of the etries i the table are FALSE. For example, if a graph is used to represet a street map like Mahatta i which most streets ru E/W or N/S, each itersectio is attached to oly 4 streets ad E < 4* V. If there are 3000 itersectios, the table has 9,000,000 etries of which oly 12,000 are TRUE. 19
20 Udirected Graph / Adjacecy Matrix
21 Directed Graph / Adjacecy Matrix
22 Weighted, Directed Graph / Adjacecy Matrix
23 Adjacecy Matrix Performace Storage requiremet: O( V 2 ) Performace: getdegree ( u ) isadjacetto( u, v ) getadjacet( u ) 23
24 Adjacecy List Implemetatio If the graph is sparse, the keepig a list of adjacet vertices for each vertex saves space. Adjacecy Lists are the commoly used represetatio. The lists may be stored i a data structure or i the Vertex object itself. q Vector of lists: A vector of lists of vertices. The i- th elemet of the vector is a list, L i, of the vertices adjacet to v i. If the graph is sparse, the the space requiremet is O( E + V ), liear i the size of the graph If the graph is dese, the the space requiremet is O( V 2 ) 24
25 Vector of Lists
26 Adjacecy List Performace Storage requiremet: Performace: getdegree( u ) isadjacetto( u, v ) getadjacet( u ) 26
27 Graph Traversals Like trees, graphs ca be traversed breadthfirst or depth-first. q Use stack (or recursio) for depth-first traversal q Use queue for breadth-first traversal Ulike trees, we eed to specifically guard agaist repeatig a path from a cycle. Mark each vertex as visited whe we ecouter it ad do ot cosider visited vertices more tha oce. 27
28 Graph Traversals Both take time: O(V+E) 28 Slide by Rose Hoberma (CMU)
29 Breadth-First Traversal void bfs() { Queue<Vertex> q; Vertex u, w; } for all v i V, d[v] = // mark each vertex uvisited q.equeue(startvertex); // start with ay vertex d[startvertex] = 0; // mark visited while (!q.isempty() ) { u = q.dequeue( ); for each Vertex w adjacet to u { if (d[w] == ) { // w ot marked as visited d[w] = d[u]+1; // mark visited path[w] = u; // where we came from q.equeue(w); } } } 29
30 Breadth-First Example v1 0 1v1 v3 q v1 v2 v3 v4 u v2 1v1 v5 v4 2v2 BFS Traversal v1 v2 v3 v4 30
31 Uweighted Shortest Path Problem Uweighted shortest-path problem: Give as iput a uweighted graph, G = ( V, E ), ad a distiguished startig vertex, s, fid the shortest uweighted path from s to every other vertex i G. After ruig BFS algorithm with s as startig vertex, the legth of the shortest path legth from s to i is give by d[i]. If d[i] =, the there is o path from s to i. The path from s to i is give by traversig path[] backwards from i back to s. 31
32 Recursive Depth First Traversal void dfs() { } for (each v Î V) dfs(v) void dfs(vertex v) { } if (!v.visited) { } v.visited = true; for each Vertex w adjacet to v) if (!w.visited ) dfs(w) 32
33 DFS with explicit stack void dfs() { } Stack<Vertex> s; Vertex u, w; s.push(startvertex); startvertex.visited = true; while (!s.isempty() ) { } u = s.pop(); for each Vertex w adjacet to u { } if (!w.visited) { w.visited = true; s.push(w); 33
34 DFS Example v1 v3 s v1 v2 v4 v3 u v2 v5 v4 DFS Traversal v1 v3 v2 v4 34
35 Traversal Performace What is the performace of DF ad BF traversal? Each vertex appears i the stack or queue exactly oce i the worst case. Therefore, the traversals are at least O( V ). However, at each vertex, we must fid the adjacet vertices. Therefore, df- ad bftraversal performace depeds o the performace of the getadjacet operatio. 35
36 GetAdjacet Method 1: Look at every vertex (except u), askig are you adjacet to u? List<Vertex> L; for each Vertex v except u if (v.isadjacetto(u)) L.push_back(v); Assumig O(1) performace for push_back ad isadjacetto, the getadjacet has O( V ) performace ad traversal performace is O( V 2 ); 36
37 GetAdjacet (2) Method 2: Look oly at the edges which impige o u. Therefore, at each vertex, the umber of vertices to be looked at is D(u), the degree of the vertex This approach is O( D( u ) ). The traversal performace is O( V å i= 1 D( vi )) = O ( E ) sice getadjacet is doe O( V ) times. However, i a discoected graph, we must still look at every vertex, so the performace is O( V + E ). 37
38 Number of Edges Theorem: The umber of edges i a udirected graph G = (V,E ) is O( V 2 ) Proof: Suppose G is fully coected. Let p = V. The we have the followig situatio: vertex coected to 1 2,3,4,5,, p 2 1,3,4,5,, p p 1,2,3,4,,p-1 q There are p(p-1)/2 = O( V 2 ) edges. So O( E ) = O( V 2 ). 38
39 Weighted Shortest Path Problem Sigle-source shortest-path problem: Give as iput a weighted graph, G = ( V, E ), ad a distiguished startig vertex, s, fid the shortest weighted path from s to every other vertex i G. Use Dijkstra s algorithm Keep tetative distace for each vertex givig shortest path legth usig vertices visited so far. Record vertex visited before this vertex (to allow pritig of path). At each step choose the vertex with smallest distace amog the uvisited vertices (greedy algorithm). 39
40 Dijkstra s Algorithm The pseudo code for Dijkstra s algorithm assumes the followig structure for a Vertex object class Vertex { public List adj; //Adjacecy list public boolea kow; public DisType dist; //DistType is probably it public Vertex path; //Other fields ad methods as eeded } 40
41 Dijkstra s Algorithm void dijksra(vertex start) { for each Vertex v i V { v.dist = Iteger.MAX_VALUE; v.kow = false; v.path = ull; } start.distace = 0; } while there are ukow vertices { v = ukow vertex with smallest distace v.kow = true; for each Vertex w adjacet to v if (!w.kow) if (v.dist + weight(v, w)< w.distace){ decrease(w.dist to v.dist+weight(v, w)) w.path = v; } } 41
42 Dijkstra Example v1 3 v2 v v4 v3 1 v6 3 v v5 v10 1 v9 42
43 Correctess of Dijkstra s Algorithm The algorithm is correct because of a property of shortest paths: If P k = v 1, v 2,..., v j, v k, is a shortest path from v 1 to v k, the P j = v 1, v 2,..., v j, must be a shortest path from v 1 to v j. Otherwise P k would ot be as short as possible sice P k exteds P j by just oe edge (from v j to v k ) Also, P j must be shorter tha P k (assumig that all edges have positive weights). So the algorithm must have foud P j o a earlier iteratio tha whe it foud P k. i.e. Shortest paths ca be foud by extedig earlier kow shortest paths by sigle edges, which is what the algorithm does. 43
44 Ruig Time of Dijkstra s Algorithm The ruig time depeds o how the vertices are maipulated. The mai while loop rus O( V ) time (oce per vertex) Fidig the ukow vertex with smallest distace (iside the while loop) ca be a simple liear sca of the vertices ad so is also O( V ). With this method the total ruig time is O ( V 2 ). This is acceptable (ad perhaps optimal) if the graph is dese ( E = O ( V 2 ) ) sice it rus i liear time o the umber of edges. If the graph is sparse, ( E = O ( V ) ), we ca use a priority queue to select the ukow vertex with smallest distace, usig the deletemi operatio (O( lg V )). We must also decrease the path legths of some ukow vertices, which is also O( lg V ). The deletemi operatio is performed for every vertex, ad the decrease path legth is performed for every edge, so the ruig time is O( E lg V + V lg V ) = O( ( V + E ) lg V ) = O( E lg V ) if all vertices are reachable from the startig vertex 44
45 Dijkstra ad Negative Edges Note i the previous discussio, we made the assumptio that all edges have positive weight. If ay edge has a egative weight, the Dijkstra s algorithm fails. Why is this so? Suppose a vertex, u, is marked as kow. This meas that the shortest path from the startig vertex, s, to u has bee foud. However, it s possible that there is egatively weighted edge from a ukow vertex, v, back to u. I that case, takig the path from s to v to u is actually shorter tha the path from s to u without goig through v. Other algorithms exist that hadle edges with egative weights for weighted shortest-path problem. 45
46 Directed Acyclic Graphs A directed acyclic graph is a directed graph with o cycles. A strict partial order R o a set S is a biary relatio such that q for all aîs, ara is false (irreflexive property) q for all a,b,c ÎS, if arb ad brc the arc is true (trasitive property) To represet a partial order with a DAG: q represet each member of S as a vertex q for each pair of vertices (a,b), isert a edge from a to b if ad oly if arb 46
47 Example DAG Uderwear Pats Belt Shirt Tie Socks Shoes Watch a DAG implies a orderig o evets Jacket 47 Slide by Rose Hoberma (CMU)
48 Example DAG Uderwear Pats Belt Shirt Tie Jacket Socks Shoes Watch I a complex DAG, it ca be hard to fid a schedule that obeys all the costraits. 48 Slide by Rose Hoberma (CMU)
49 More Defiitios Vertex i is a predecessor of vertex j if ad oly if there is a path from i to j. Vertex i is a immediate predecessor of vertex j if ad oly if ( i, j ) is a edge i the graph. Vertex j is a successor of vertex i if ad oly if there is a path from i to j. Vertex j is a immediate successor of vertex i if ad oly if ( i, j ) is a edge i the graph. The idegree of a vertex, v, is the umber of edges (u, v), i.e. the umber of edges that come ito v. 49
50 Topological Orderig A topological orderig of the vertices of a DAG G = (V,E) is a liear orderig such that, for vertices i, j ÎV, if i is a predecessor of j, the i precedes j i the liear order, i.e. if there is a path from v i to v j, the v i comes before v j i the liear order 50
51 Topological Sort For a directed acyclic graph G = (V,E) A topological sort is a orderig of all of G s vertices v 1, v 2,, v such that... Formally: for every edge (v i,v k ) i E, i<k. Visually: all arrows are poitig to the right 51 Slide by Rose Hoberma (CMU)
52 Topological Sort There are ofte may possible topological sorts of a give DAG Topological orders for this DAG : 1,2,5,4,3,6,7 2,1,5,4,7,3,6 2,5,1,4,7,3,6 Etc Each topological order is a feasible schedule. 52 Slide by Rose Hoberma (CMU)
53 Topological Sorts for Cyclic Graphs? Impossible! If v ad w are two vertices o a cycle, there exist paths from v to w ad from w to v. Ay orderig will cotradict oe of these paths 53 Slide by Rose Hoberma (CMU)
54 Topological sort algorithm Algorithm q Assume idegree is stored with each ode. q Repeat util o odes remai: Choose a root ad output it. Remove the root ad all its edges. Performace q O(V 2 + E), if liear search is used to fid a root. 54 Slide by Rose Hoberma (CMU)
55 Better topological sort Algorithm: q Sca all odes, pushig roots oto a stack. q Repeat util stack is empty: Pop a root r from the stack ad output it. For all odes such that (r,) is a edge, decremet s idegree. If 0 the push oto the stack. O( V + E ), so still O(V 2 ) i worst case, but better for sparse graphs. Q: Why is this algorithm correct? 55 Slide by Rose Hoberma (CMU)
56 Correctess Clearly ay orderig produced by this algorithm is a topological order But... Does every DAG have a topological order, ad if so, is this algorithm guarateed to fid oe? 56 Slide by Rose Hoberma (CMU)
57 Exercise Prove: q This algorithm ever gets stuck, i.e. if there are uvisited odes the at least oe of them has a idegree of zero. Approach: q Prove that if at ay poit there are usee vertices but oe of them have a idegree of 0, a cycle must exist, cotradictig our assumptio of a DAG. 57 Based o slide by Rose Hoberma (CMU)
58 Topological Sort 58
59 Ruig Time of TopSort 1. At most, each vertex is equeued just oce, so there are O( V ) costat time queue operatios. 2. The body of the for loop is executed at most oce per edges = O( E ) 3. The iitializatio is proportioal to the size of the graph if adjacecy lists are used = O( E + V ) 4. The total ruig time is therefore O ( E + V ) 60
Basic Graph Definitions
 CMSC 341 Graphs Basic Graph Definitions A graph G = (V,E) consists of a finite set of vertices, V, and a finite set of edges, E. Each edge is a pair (v,w) where v, w V. V and E are sets, so each vertex
CMSC 341 Graphs Basic Graph Definitions A graph G = (V,E) consists of a finite set of vertices, V, and a finite set of edges, E. Each edge is a pair (v,w) where v, w V. V and E are sets, so each vertex
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
CIS 121. Introduction to Trees
 CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
Priority Queues. Binary Heaps
 Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Minimum Spanning Trees
 Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Heaps. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Graphs ORD SFO LAX DFW
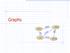 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Graphs ORD SFO LAX DFW. Lecture notes adapted from Goodrich and Tomassia. 3/14/18 10:28 AM Graphs 1
 Graphs 337 1843 1743 1233 802 Lecture otes adapted from Goodrich ad Tomassia 3/14/18 10:28 AM Graphs 1 Graph A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs
Graphs 337 1843 1743 1233 802 Lecture otes adapted from Goodrich ad Tomassia 3/14/18 10:28 AM Graphs 1 Graph A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
DATA STRUCTURES. amortized analysis binomial heaps Fibonacci heaps union-find. Data structures. Appetizer. Appetizer
 Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sorting 9/15/2009. Sorting Problem. Insertion Sort: Soundness. Insertion Sort. Insertion Sort: Running Time. Insertion Sort: Soundness
 9/5/009 Algorithms Sortig 3- Sortig Sortig Problem The Sortig Problem Istace: A sequece of umbers Objective: A permutatio (reorderig) such that a ' K a' a, K,a a ', K, a' of the iput sequece The umbers
9/5/009 Algorithms Sortig 3- Sortig Sortig Problem The Sortig Problem Istace: A sequece of umbers Objective: A permutatio (reorderig) such that a ' K a' a, K,a a ', K, a' of the iput sequece The umbers
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
BST Sequence of Operations
 Splay Trees Problems with BSTs Because the shape of a BST is determied by the order that data is iserted, we ru the risk of trees that are essetially lists 12 21 20 32 24 37 15 40 55 56 77 2 BST Sequece
Splay Trees Problems with BSTs Because the shape of a BST is determied by the order that data is iserted, we ru the risk of trees that are essetially lists 12 21 20 32 24 37 15 40 55 56 77 2 BST Sequece
Data Structures Week #5. Trees (Ağaçlar)
 Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Algorithm. Counting Sort Analysis of Algorithms
 Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Basic allocator mechanisms The course that gives CMU its Zip! Memory Management II: Dynamic Storage Allocation Mar 6, 2000.
 5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Lecture Notes 6 Introduction to algorithm analysis CSS 501 Data Structures and Object-Oriented Programming
 Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
Greedy Algorithms. Interval Scheduling. Greedy Algorithms. Interval scheduling. Greedy Algorithms. Interval Scheduling
 Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Design and Analysis of Algorithms Notes
 Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
A graphical view of big-o notation. c*g(n) f(n) f(n) = O(g(n))
 ca see that time required to search/sort grows with size of We How do space/time eeds of program grow with iput size? iput. time: cout umber of operatios as fuctio of iput Executio size operatio Assigmet:
ca see that time required to search/sort grows with size of We How do space/time eeds of program grow with iput size? iput. time: cout umber of operatios as fuctio of iput Executio size operatio Assigmet:
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Lower Bounds for Sorting
 Liear Sortig Topics Covered: Lower Bouds for Sortig Coutig Sort Radix Sort Bucket Sort Lower Bouds for Sortig Compariso vs. o-compariso sortig Decisio tree model Worst case lower boud Compariso Sortig
Liear Sortig Topics Covered: Lower Bouds for Sortig Coutig Sort Radix Sort Bucket Sort Lower Bouds for Sortig Compariso vs. o-compariso sortig Decisio tree model Worst case lower boud Compariso Sortig
Computer Science Foundation Exam. August 12, Computer Science. Section 1A. No Calculators! KEY. Solutions and Grading Criteria.
 Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
CS200: Hash Tables. Prichard Ch CS200 - Hash Tables 1
 CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
Solution printed. Do not start the test until instructed to do so! CS 2604 Data Structures Midterm Spring, Instructions:
 CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
Name of the Student: Unit I (Logic and Proofs) 1) Truth Table: Conjunction Disjunction Conditional Biconditional
 SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Graph: representation and traversal
 Graph: representation and traversal CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang! Acknowledgement The set of slides have use materials from the following resources Slides for textbook
Graph: representation and traversal CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang! Acknowledgement The set of slides have use materials from the following resources Slides for textbook
Computers and Scientific Thinking
 Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
Graph Representation
 Graph Representation Adjacency list representation of G = (V, E) An array of V lists, one for each vertex in V Each list Adj[u] contains all the vertices v such that there is an edge between u and v Adj[u]
Graph Representation Adjacency list representation of G = (V, E) An array of V lists, one for each vertex in V Each list Adj[u] contains all the vertices v such that there is an edge between u and v Adj[u]
Data diverse software fault tolerance techniques
 Data diverse software fault tolerace techiques Complemets desig diversity by compesatig for desig diversity s s limitatios Ivolves obtaiig a related set of poits i the program data space, executig the
Data diverse software fault tolerace techiques Complemets desig diversity by compesatig for desig diversity s s limitatios Ivolves obtaiig a related set of poits i the program data space, executig the
CS211 Fall 2003 Prelim 2 Solutions and Grading Guide
 CS11 Fall 003 Prelim Solutios ad Gradig Guide Problem 1: (a) obj = obj1; ILLEGAL because type of referece must always be a supertype of type of object (b) obj3 = obj1; ILLEGAL because type of referece
CS11 Fall 003 Prelim Solutios ad Gradig Guide Problem 1: (a) obj = obj1; ILLEGAL because type of referece must always be a supertype of type of object (b) obj3 = obj1; ILLEGAL because type of referece
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Data Structures and Algorithms. Chapter 7. Graphs
 1 Data Structures and Algorithms Chapter 7 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
1 Data Structures and Algorithms Chapter 7 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
Basic Graph Algorithms (CLRS B.4-B.5, )
 Basic Graph Algorithms (CLRS B.-B.,.-.) Basic Graph Definitions A graph G = (V,E) consists of a finite set of vertices V and a finite set of edges E. Directed graphs: E is a set of ordered pairs of vertices
Basic Graph Algorithms (CLRS B.-B.,.-.) Basic Graph Definitions A graph G = (V,E) consists of a finite set of vertices V and a finite set of edges E. Directed graphs: E is a set of ordered pairs of vertices
top() Applications of Stacks
 CS22 Algorithms ad Data Structures MW :00 am - 2: pm, MSEC 0 Istructor: Xiao Qi Lecture 6: Stacks ad Queues Aoucemets Quiz results Homework 2 is available Due o September 29 th, 2004 www.cs.mt.edu~xqicoursescs22
CS22 Algorithms ad Data Structures MW :00 am - 2: pm, MSEC 0 Istructor: Xiao Qi Lecture 6: Stacks ad Queues Aoucemets Quiz results Homework 2 is available Due o September 29 th, 2004 www.cs.mt.edu~xqicoursescs22
Major CSL Write your name and entry no on every sheet of the answer script. Time 2 Hrs Max Marks 70
 NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
Introduction to Graphs. common/notes/ppt/
 Introduction to Graphs http://people.cs.clemson.edu/~pargas/courses/cs212/ common/notes/ppt/ Introduction Graphs are a generalization of trees Nodes or verticies Edges or arcs Two kinds of graphs irected
Introduction to Graphs http://people.cs.clemson.edu/~pargas/courses/cs212/ common/notes/ppt/ Introduction Graphs are a generalization of trees Nodes or verticies Edges or arcs Two kinds of graphs irected
CSE 417: Algorithms and Computational Complexity
 Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
CSC 172 Data Structures and Algorithms. Lecture 24 Fall 2017
 CSC 172 Data Structures and Algorithms Lecture 24 Fall 2017 ANALYSIS OF DIJKSTRA S ALGORITHM CSC 172, Fall 2017 Implementation and analysis The initialization requires Q( V ) memory and run time We iterate
CSC 172 Data Structures and Algorithms Lecture 24 Fall 2017 ANALYSIS OF DIJKSTRA S ALGORITHM CSC 172, Fall 2017 Implementation and analysis The initialization requires Q( V ) memory and run time We iterate
CSE 5311 Notes 16: Matrices
 CSE 5311 Notes 16: Matrices STRASSEN S MATRIX MULTIPLICATION Matrix additio: takes scalar additios. Everyday atrix ultiply: p p Let = = p. takes p scalar ultiplies ad -1)p scalar additios. Best lower boud
CSE 5311 Notes 16: Matrices STRASSEN S MATRIX MULTIPLICATION Matrix additio: takes scalar additios. Everyday atrix ultiply: p p Let = = p. takes p scalar ultiplies ad -1)p scalar additios. Best lower boud
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
The Magma Database file formats
 The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
COSC 1P03. Ch 7 Recursion. Introduction to Data Structures 8.1
 COSC 1P03 Ch 7 Recursio Itroductio to Data Structures 8.1 COSC 1P03 Recursio Recursio I Mathematics factorial Fiboacci umbers defie ifiite set with fiite defiitio I Computer Sciece sytax rules fiite defiitio,
COSC 1P03 Ch 7 Recursio Itroductio to Data Structures 8.1 COSC 1P03 Recursio Recursio I Mathematics factorial Fiboacci umbers defie ifiite set with fiite defiitio I Computer Sciece sytax rules fiite defiitio,
Speeding-up dynamic programming in sequence alignment
 Departmet of Computer Sciece Aarhus Uiversity Demark Speedig-up dyamic programmig i sequece aligmet Master s Thesis Dug My Hoa - 443 December, Supervisor: Christia Nørgaard Storm Pederse Implemetatio code
Departmet of Computer Sciece Aarhus Uiversity Demark Speedig-up dyamic programmig i sequece aligmet Master s Thesis Dug My Hoa - 443 December, Supervisor: Christia Nørgaard Storm Pederse Implemetatio code
Lecture 28: Data Link Layer
 Automatic Repeat Request (ARQ) 2. Go ack N ARQ Although the Stop ad Wait ARQ is very simple, you ca easily show that it has very the low efficiecy. The low efficiecy comes from the fact that the trasmittig
Automatic Repeat Request (ARQ) 2. Go ack N ARQ Although the Stop ad Wait ARQ is very simple, you ca easily show that it has very the low efficiecy. The low efficiecy comes from the fact that the trasmittig
Chapter 11. Friends, Overloaded Operators, and Arrays in Classes. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Chapter 14. Graphs Pearson Addison-Wesley. All rights reserved 14 A-1
 Chapter 14 Graphs 2011 Pearson Addison-Wesley. All rights reserved 14 A-1 Terminology G = {V, E} A graph G consists of two sets A set V of vertices, or nodes A set E of edges A subgraph Consists of a subset
Chapter 14 Graphs 2011 Pearson Addison-Wesley. All rights reserved 14 A-1 Terminology G = {V, E} A graph G consists of two sets A set V of vertices, or nodes A set E of edges A subgraph Consists of a subset
CS Polygon Scan Conversion. Slide 1
 CS 112 - Polygo Sca Coversio Slide 1 Polygo Classificatio Covex All iterior agles are less tha 180 degrees Cocave Iterior agles ca be greater tha 180 degrees Degeerate polygos If all vertices are colliear
CS 112 - Polygo Sca Coversio Slide 1 Polygo Classificatio Covex All iterior agles are less tha 180 degrees Cocave Iterior agles ca be greater tha 180 degrees Degeerate polygos If all vertices are colliear
Analysis Metrics. Intro to Algorithm Analysis. Slides. 12. Alg Analysis. 12. Alg Analysis
 Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
11/22/2016. Chapter 9 Graph Algorithms. Introduction. Definitions. Definitions. Definitions. Definitions
 Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Σ P(i) ( depth T (K i ) + 1),
 EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
Appendix D. Controller Implementation
 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Appedix D Cotroller Implemetatio Cotroller Implemetatios Combiatioal logic (sigle-cycle); Fiite state machie (multi-cycle, pipelied);
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Iterface 5 th Editio Appedix D Cotroller Implemetatio Cotroller Implemetatios Combiatioal logic (sigle-cycle); Fiite state machie (multi-cycle, pipelied);
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Data Structures Week #9. Sorting
 Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Massachusetts Institute of Technology Lecture : Theory of Parallel Systems Feb. 25, Lecture 6: List contraction, tree contraction, and
 Massachusetts Istitute of Techology Lecture.89: Theory of Parallel Systems Feb. 5, 997 Professor Charles E. Leiserso Scribe: Guag-Ie Cheg Lecture : List cotractio, tree cotractio, ad symmetry breakig Work-eciet
Massachusetts Istitute of Techology Lecture.89: Theory of Parallel Systems Feb. 5, 997 Professor Charles E. Leiserso Scribe: Guag-Ie Cheg Lecture : List cotractio, tree cotractio, ad symmetry breakig Work-eciet
Data Structures and Algorithms Part 1.4
 1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
1. Graph and Representation
 Chapter Graphs Tree Root Direction: parent-child relationships No cycles Graph Vertices + Edges No tree restrictions Examples World Wide Web Maps. Graph and Representation A graph G: a pair (V, E) vertices
Chapter Graphs Tree Root Direction: parent-child relationships No cycles Graph Vertices + Edges No tree restrictions Examples World Wide Web Maps. Graph and Representation A graph G: a pair (V, E) vertices
How do we evaluate algorithms?
 F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
CMSC 380. Graph Terminology and Representation
 CMSC 380 Graph Terminology and Representation GRAPH BASICS 2 Basic Graph Definitions n A graph G = (V,E) consists of a finite set of vertices, V, and a finite set of edges, E. n Each edge is a pair (v,w)
CMSC 380 Graph Terminology and Representation GRAPH BASICS 2 Basic Graph Definitions n A graph G = (V,E) consists of a finite set of vertices, V, and a finite set of edges, E. n Each edge is a pair (v,w)
What are we going to learn? CSC Data Structures Analysis of Algorithms. Overview. Algorithm, and Inputs
 What are we goig to lear? CSC316-003 Data Structures Aalysis of Algorithms Computer Sciece North Carolia State Uiversity Need to say that some algorithms are better tha others Criteria for evaluatio Structure
What are we goig to lear? CSC316-003 Data Structures Aalysis of Algorithms Computer Sciece North Carolia State Uiversity Need to say that some algorithms are better tha others Criteria for evaluatio Structure
Reliable Transmission. Spring 2018 CS 438 Staff - University of Illinois 1
 Reliable Trasmissio Sprig 2018 CS 438 Staff - Uiversity of Illiois 1 Reliable Trasmissio Hello! My computer s ame is Alice. Alice Bob Hello! Alice. Sprig 2018 CS 438 Staff - Uiversity of Illiois 2 Reliable
Reliable Trasmissio Sprig 2018 CS 438 Staff - Uiversity of Illiois 1 Reliable Trasmissio Hello! My computer s ame is Alice. Alice Bob Hello! Alice. Sprig 2018 CS 438 Staff - Uiversity of Illiois 2 Reliable
