Discretization of spatial objects
|
|
|
- Brent Campbell
- 5 years ago
- Views:
Transcription
1 Discretization of spatial objects Mosaics, Tessellations and Lattices Discretization is the process of partitioning continuous space, either lines or areas, into pieces. This process is referred to as tiling in the case of two-dimensional spatial units, or segmenting in the case of lines. Mosaics or tiles of zones of irregular and varied shape and size may be created via various processes. Originally conceived as polygons with four equal corners, as implied by the Greek word tetara or Latin word tessella, mosaics also can be made up of other regular geometric figures or a mixture of different types. Tessellations (sometimes in the computer graphics field called meshes), are sets of connected discrete two-dimensional units: Tessellations may be regular or irregular in geometry: a regular tessellation (for example, grid squares) is an (infinitely) repeatable pattern of a regular polygon (two-dimensional figure) or polyhedron (three-dimensional figure). This cellular decomposition implies every point in space is assigned to only one cell. an irregular tessellation is an (infinitely) extending configuration of polygons or polyhedra of varied shape and size. Irregular planar tessellations may also be regarded and represented as topological two-cells. Irregular tessellations are used in areas such as: zones for social, economic, and demographic data administrative or political units surface modelling using triangles
2 partitions of a large geographic database man-made phenomena like land parcels irregular sampling of a continuous spatial distribution wireframe modelling of buildings Regular tessellations are encountered in: image data from reniote sensing data compilations from maps by grid squares organization of map libraries data generated by photogrammetric systems as lattices of points uniform sampling of a continuous spatial distribution The underlying semantic questions regarding what is in (this) space or at (this) point and what is the location of (this) object are not in a one-to-one relationship with geometric form. An object can be positioned in Cartesian coordinate space, or it could be referenced by location within a hexagon. Grid squares are often used to record the nature of space, but the square is just the extreme, perfectly symmetrical case for all tessellations. Lattices are point entities arranged over space in a regular, perhaps square or hexagonal, pattern: The lattices may be seen as the intersections of the grid lines or as the centres of a set of squares (c). Or, they may consist of a quinconcial pattern made up of the points and middle for a set of squares. Originally the word lattice referred to thin strips of wood or metal, crossing diagonally (d), and capable of forming different patterns or networks.
3 Moreover, the regular tessellations may be seen as different patterns of points. The patterns of the sets of points may change via application of a linear transformation, for example, tilting the y-axis, just as a lattice of wood pieces anchored by pins at the crossings can be changed into different forms by pushing or pulling in one or the other coordinate axis. Thus, sets of rectangles or parallelograms can be made from squares (e) by remapping the centroids of the squares. And a hexagonal arrangement of points can become a square grid of points or vice versa. There is not a one-to-one relationship between grid squares and a square lattice, for a square mosaic can be changed into a set of equidistant points arranged in a hexagonal pattern (or other forms), although there is a duality of zero (lattice points) and two cell (tessellation polygons) units. Scale and resolution The basic spatial units of a tessellation can vary in size, shape, orientation and spacing. Also, for a given theme, several tessellations can exist, representing different scales of observation, or aggregations or subdivisions from one initial scale of observation: Variable resolution and scale: (a) different scales, (b) different scales for hexagons, (c) variable resolution hexagons, (d) varying resolutions at one scale for point data. For regularly shaped two-dimensional units the structuring is akin to a pyramid; for irregular shapes, the new larger units produced by combining smaller units, as in creating school districts from census tracts, will not have a shape consistent across the different scales. Varying scale is seen for lattices in different point densities per unit area.
4 The basic unit may vary in size for a given theme for a given scale. These concepts are met in theoretical formulations like the different sizes of hexagons for central place theory (b and c), a set of propositions which, among other things, addresses the question of the size and shape of market areas for services provided from towns. It also arises for practical applications like surface modelling triangulations. Irregular tessellations generally have implicitly variable spatial resolution (c), but regular tessellations with variable size units for one theme have to be produced from the smallest scale by subdivision. Tessellations, mosaics and lattices are not only to be seen as spatial units for recording data, but also as devices for facilitating access to databases for continuous space. While any piece of the earth can conceivably be used for addressing and retrieval, regular tilings have some advantages for this purpose. The Geometry of Regular Tessellations Of the many regular geometric figures, from 3 to N sides, the square, triangle and hexagon are those currently most likely to be generally encountered in spatial data contexts. Some, like the pentagon, appear in special circumstances. The square has some practical advantages historically, being the unit used in graph paper and mechanical printing devices. The hexagon has utility in theory and practice where adjacency is an important property or where packing of geometric figures into space is important. The triangle has a property of being the most primitive polygon, that is, it cannot be further subdivided into a different figure, and it can readily have varying shape based on angles or length of sides conditions. Comparisons of the value of different tiling units are best made on the basis of certain standard properties. In examining the geometry of regular tilings we will consider: shape adjacency connectivity orientation self-similarity decomposability packing properties Shape is the geometry of the figure's different number of sides, albeit that particular instances of a particular type of figure may have different shapes, where there is no tight restriction on the length of sides or the angles, as for triangles. Shape for regular figures is identified by the number of edges at a vertex and the number of vertices.
5 Adjacency refers to the conditions of touching for repeated instances of the basic figure. The contiguity may be at the sides (edges), or corners (vertices), or both. This situation varies from the sides only for hexagons, to both vertices and edges for triangles and squares or rectangles. Metric measurements can be used to distinguish different figures - the adjacency distance is the distance between the centroid of one tile and a neighbour, and the adjacency number is the number of different adjacency distances. The hexagon has one such distance, six in number (one for each equidistant neighbour). The square has two, and the equilateral triangle has three different distances. Related to adjacency, but considering only the conditions at the intersections, for some applications, like transportation, the hexagon has the connectivity advantages of having junctions at only three edges, unlike the four for a regular grid, as in an American-style city block street system. For most purposes, though, the polygon space adjacency is of more interest that the intersection connectivity patterns. The tile orientation, defined as the base relative to coordinate axes, is uniform for the hexagon and square, but not so for the triangle as not all instances of triangles in a tessellation can have the base parallel to either the x or y coordinate axes. 'I'iles with the same orientation can be transformed into each other by translations, that is, by shifting along the x- and y-axes, without necessitating rotation or reflection.
6 If the basic figure shape is similar to that produced by aggregations to a higher level, then the property of self-similarity exists. This is unlimited for regular figures which have each side on an infinitely straight line composed entirely of edges. This condition is seen clearly in the case of the tiles touching at corners (opus quadratum) as opposed to the bricklayer's scheme (opus lateritum) with only horizontal unbroken lines (Figure 6.5a). However, only two tessellation types, the square and equilatral triangle, with identical side lengths, and two tessellation figures with unequal side lengths, the isosceles and the degrees right angle triangles, meet this condition. It is also of interest to examine changing conditions if the figures are decomposed into smaller units or combined to larger units. The square and equilateral triangle can be decomposed into units of the same shape, but the hexagon cannot; it can be split into six equilateral triangles. Indeed, as (b) demonstrates, the aggregation of seven hexagons produces a rosette, while the aggregation of equilateral triangles produces polygons if pairs are taken, and higher-level triangles if four basic triangles are combined. While the hexagon is not decomposable with selfsimilarity, it can be used at different scales, rather as a lattice pattern, without nesting. Only the square can be decomposed into smaller or assembled into larger tiles of the same shape and orientation, and be compatible with the orthogonal axes of Cartesian coordinate systems. The overall pattern of how the repeated regular figures pack space is an important condition in engineering for properties like stress, and is also important for living organisms in their effectiveness in the use of space. A structurally stable situation (c) is demonstrated by the relationships of a set of circles at right angles, at oblique angles representing rotation of one of the two coordinate axes, and then displacement to oblique axes where the vertical spacing is half the horizontal. It is not surprising, though, on the basis of this review of properties, that the square figure dominates the world of regular tessellations for spatial information systems for two- or three-dimensional entities (except if a single sphere is to be partitioned). The square has simple and valuable conditions of equality of sides, decomposability, and stability for orientation and aggregation. So the square appears
7 in the form of arrays of picture elements, grid cell data recording, lattices for elevation data, and electronic data capture and displays. The hexagon is more complex although it has nice properties of edge touching and economy of packing space. In theory it has had many uses, but not in practice. However, recently it has made an appearance as the data unit for one particular spatial database. The triangle has advantages of being the most primitive polygon, and does appear in several practical contexts, although in the form of irregular rather than regular triangles. Fixed Spatial Resolutions: Regular Cell Grids The commonly encountered organization of data into an array of regular cells, almost always, but not necessarily, square, is regarded as practically straightforward, but conceptually does not explicity deal with questions of the type: Where do I find this particular entity? The basic unit of the square handles both location, geographic or arbitrary, and the attributes of the location. Often known as raster encoding of earth features, this cell array approach contrasts with the vector object-oriented encodings, having some practical advantages, as well as some limitations. Data encoding Some fundamental considerations to be examined regarding grid-cell data organization are: 1. The existence of an a priori fixed resolution. 2. The method of determining what attribute is in a cell. 3. The level of measurement used for the attributes. 4. Limitations in recording precisely point or line features. 5. The absence of recording coordinates for features. 6. The lack of explicit topology. 7. The flexibility in undertaking many operations easily. 8. A match with a field view of the world. Spatial properties Spatial relationships are implicit in the data, but with only a few exceptions do the software systems for grid cell data allow direct handling of relationships between entities. Metrical distance relations along orthogonal axes are readily derived, although not without limitations, from the differences between x and y coordinates (row and column values), and other distances are computed as the hypotenuse of right angled triangles. While axial and diagonal lines can be measured by cell increments without loss of precision, this is not so for other hypotenuses. Thus, perimeter measures for areal objects or lengths for linear features may be severely erroneous. Shapes can be approximated by observing orientations of lines of cells relative to those of
8 neighbours, assuming that the resolution is good enough to produce sufficient unambiguous data. Metrical spatial properties can be readily dealt with by square cell tessellations, bearing in mind the resolution implied by the cell size. Distances are harder to obtain for hexagons, because the centres of the cells are arranged symmetrically along three coordinate axes, but properties based on neighbours are much easier because there are no corner adjacencies. Distances and adjacencies are more awkward for sets of equilateral triangles, because they have six triangles touching at corners and three different distance values for each triangle centre. Graph properties of connectivity have to be explicitly recorded for cells containing nodes, and details of direction of edges leaving nodes (necessary in order to create a precise graph) must also be encoded. Consequently, the desirable situation is a combination of cells and vector representation of point and line elements within cells. Details for points and lines within a grid cell could be retained by particular coding techniques, or by linking the grid cell to other data by reference to the grid cell identifier. Some techniques have been devised to record information explicitly in a grid framework for line and polygon entities. Thus, the directional coding presented in section 4.5 is sometimes used for boundary line or linear feature representation. Topological properties are only indirectly dealt with by the regular tessellation forms, because they do not treat phenomena as entities. Of course, there are properties of adjacency and connectivity among cells, but qualitative spatial relationships for entities must be derived from the data that are recorded. The topological properties of non-confiectivity may be violated, such as the apparent joining of highways or touching of inner and outer boundaries of polygons. The graph property of existence of holes can be determined by calculating the distance to the nearest edge of a polygon (a set of cells). Cell encoding forces pattern to be inferred from the data values for adjacent cells, but it does facilitate the process as it directly establishes neighbours and neighbourhoods. If cells are square, then eight touching pairs exist in the immediate ring around a cell; other situations may take in other cells, such as the neighbours of a block of four cells. Yet, unlike for topological encoding, the identification of neighboujing regular cells provides little information unless the attributes of the cells are considered, such as in creating zones by finding cells of a particular attribute value. However, many operations, logical or arithmetic, are quite straightforward when working with grid cell data. Area measures simply involve counting squares, not computational geometry; distances involve subtracting, and can be readily ascertained even on diagonals. Aggregations can be made within proximity zones, and map overlay modelling using attribute information essentially does nothing more than compare attribute values for identical grid cells. At the same time, vector geometry
9 may have an advantage in that much of the space is void: for regular tessellations, the space is 'full'. Surface modelling from lattices The elevation dimension is readily manipulated and displayed by means of data for cells, although it is usual to record such data as a lattice. Such data, often referred to as digital elevation models because they are used for interpolating or extrapolating values for places in addition to the original data points, generally are themselves produced from other data by a process of gridding. Each cell or point carries data for an elevation or depth relative to a horizontal datum. Much use has been made of grid cells or lattice-point data for representing fields of varying quantities across space, whether continuous or broken. The mesh form of the data, whether the values are for grid line intersections or cell centroids, lends itself to simple linear interpolations along the x- and y-axes. The outcome is often simply an isoline map. Proximity surfaces are easily created from the mesh data by accumulating distances in (circular) zones from specified points, or in bands out from line or area objects. Smoothing of attribute values for blocks of touching cells, five or nine, provides a means of generalizing the spatial attributes which are in scalar forms of measurement. Structures for grid cell data Just as there are numerous varieties of organizing geometric and topological properties in data tables, so there are different ways of structuring regular tessellation data:
10 The common form for a basic tabular record of data for grid cells consists of a row coordinate value, a column coordinate value, possibly a cell identifier, in addition to the row-column combination, a series of values for attributes found in a cell, possibly a code value pointing to another table of data, a reference to the identifier for the nearest cell on the sides or corners. If only one attribute is of interest, then the basic table consists of a row identifier, column identifier (jointly making a space locator) and one data item: an organization reflecting each grid cell as an individual entity. The records, that is one per grid cell, can be listed sequentially in row order or column order, or, taking advantage of computer storage formats known as arrays, the entire matrix of cells can be stored (b). The matrix format may also be used if there are several data items for each grid cell. The term raster (from the German raster, meaning screen), while often used interchangeably with grid cell data, implies, though, an ordering through the whole matrix in line scan form, that is, one row followed by the others, as in the set of parallel lines making up a television picture. Another variety clusters observations in groups of like character, and then provides coordinates for each pixel (c). Conceptually, a grid encoded database looks like (d). Although often associated with a map layer concept, the overlay arrangement is not a requirement for regular tessellations as the grid-cell or pixel form suggests. However, the matrix and clustered forms are designed to work with thematic layers, meaning that the attribute data are not recorded in sequence for each and every cell. While the layering architecture is utilized for both entity-oriented and tessellation encoding of phenomena, the two types certainly do treat attribute data differently. For entity-oriented representations, attributes are separated from the spatial information in
11 most cases, whereas for regular tessellations the positional and attribute data are associated. Spatial aggregation can be achieved quite well for tessellations by combinations of adjacent cells; spatial disaggregation can be dealt with by splitting cells. Aggregations might be necessary to facilitate generalization from one resolution (geographic scale) to another. For example, the number of points in four cells can be added to get the incidence for a set of four cells, or, if the attributes are scalar, an average could be obtained. Combinations might be necessary to produce the grid cell equivalent of homogeneous regions or administrative districts. However, awkwardness arises for shapes other than the square figure. Hexagons can be subdivided into only the triangle regular figure, although this is a straightforward process; equilateral triangles may be subdivided into other triangles, but they will not always be equilateral. Triangles can be combined into parallelograms, or polygons, or hexagons depending on how many are joined; and hexagons produce rosette shapes when seven are joined together. It is not surprising, therefore, that the square cell is used for aggregating or disaggregating across scales. The resulting form, known as the pyramid model: provides a multiple scale representation, with spatial units constant for a given scale. Used often in image processing, it provides a means to remove or hide detail in order to focus on structural components like general shape, or to reveal details of form that might be hidden by too much generalization.
12 It is designed for rapid detection of global (overall, not earthly) features in a complex image. An ordinary pyramid has blocks of four cells combining to larger cells at higher levels, without overlap. A standard overlapped pyramid has 50 per cent overlap for adjacent blocks (b). A hierarchical representation has uses in image processing: for browsing at different scales, for simplifying mapping, for matching data collected at different resolutions, for access at different levels. In this way, the grid cell becomes a handy spatial indexing tool, rather than a storage unit, for space filling curves. The B -Tree: a Balanced Multiway Search Tree It is customary to classify a multiway tree by the maximum number of branches at each node, rather than the maximum number of items which may be stored at each node. If we use a multiway search tree with M possible branches at each node, then we can store up to M - 1 data items at each node. Since multiway trees are primarily used in databases, the data that are stored are usually of a fairly complex type. In each node of a multiway search tree, we may have up to M - 1 keys labeled To get the greatest efficiency gain out of a multiway search tree, we need to ensure that most of the nodes contain as much data as possible, and that the tree is as balanced as possible. There are several algorithms which approach this problem from various angles, but the most popular method is the B-tree: 1 a B-tree is a multiway search tree with a maximum of M branches at each node. The number M is called the order of the tree. 2 there is a single root node which may have as few as two children, or none at all if the root is the only node in the tree. 3 at all nodes, except the root and leaf nodes, there must be at least half the maximum number of children. 4 all leaves are on the same level. A B-tree of order 5 is shown:
13 An example of how a B-tree (or any multiway tree) is searched for an item, which is presented in B-tree and is presented not. Calculating the efficiency of a B-tree. Constructing a B-Tree The insertion method for a B-tree is somewhat different to that for the other trees we have studied, since the condition that all leaves be on the same level forces insertion into the upper part of the tree. It is easiest to learn the insertion procedure by example, so we will construct an order-5 B-tree from the list of integers: Since each node can have up to five branches, each node can store up to four keys. Therefore, the first four keys can be placed in the root, in sorted order, as shown: The fifth key, 11, will require the creation of a new node, since the root is full. In order not to violate one of the conditions on a B-tree: the root s not allowed to have only a single child, we split the root at its midpoint and create two new nodes, leaving only the middle key in the root. This gives the tree shown: We can add the next three keys wothout having to create any more nodes:
14 When we wish to add the next key, 10, it would fit into the right child of the root, but this node is full. We split the node, putting the middle key into the node s parent: Now we can insert next four keys without any problems: Inserting the key 24 causes another split and increases the number of keys in the root to three: We can now insert another five keys:
15 Insertion of the final key, 16, causes the fourth leaf from the left to split, and pushes its middle key, 13, upwards. However, the parent node is also full, so it must split as well, following the same rules. This results in a new root node, and increases the height of the tree to three levels. The completed B-tree is shown: The algorithm for insertion into a B-tree can be summarized as follows: 1. Find the node into which the new key should be inserted by searching the tree. 2. If the node is not full, insert the key into the node, using an appropriate sorting algorithm. 3. If the node is full, split the node into two and push the middle key upwards into the parent. If the parent is also full, follow the same procedure (splitting and pushing upwards) until either some space is found in a previously existing node, or a new root node is created. Although the algorithm for insertion may look straightforward on paper, it contains quite a few subtleties which only come out when you try to program it. A program implementing this insertion routine is a nontrivial affair, and could be used as the basis for a programming project. Hashing Procedures Let us denote the set of all possible key values (i.e., the universe of keys) used in a dictionary application by U. Suppose an application requires a dictionary in which elements are assigned keys from the set of small natural numbers. That is, U Z + and U is relatively small.
16 If no two elements have the same key, then this dictionary can be implemented by storing its elements in the array T[0,, U - 1]. This implementation is referred to as a direct-access table since each of the requisite DICTIONARY ADT operations - Search, Insert, and Delete - can always be performed in Q(1) time by using a given key value to index directly into T, as shown: The obvious shortcoming associated with direct-access tables is that the set U rarely has such "nice" properties. In practice, U can be quite large. This will lead to wasted memory if the number of elements actually stored in the table is small relative to U. Furthermore, it may be difficult to ensure that all keys are unique. Finally, a specific application may require that the key values be real numbers, or some symbols which cannot be used directly to index into the table. An effective alternative to direct-access tables are hash tables. A hash table is a sequentially mapped data structure that is similar to a direct-access table in that both attempt to make use of the random-access capability afforded by sequential mapping. However, instead of using a key value to directly index into the hash table, the index is computed from the key value using a hash function, which we will denote using h. This situation is depicted as follows:
17 In this figure h(k i ) is the index, or hash value, computed by h when it is supplied with key k i U. We will say that k i hashes to slot T[h(k i )] in hash table T. If we can ensure that all keys have unique hash values, then the DICTIONARY ADT operations can be implemented almost in the same way as for regular arrays. The advantages of this approach are that, if we pick the hash function properly, the size of the hash table m can be chosen so as to be proportional to the number of elements actually stored in the table n, and the key values will not be restricted to the set of small natural numbers. Furthermore, if the hash function itself can be computed in Q(1) time, then each of the DICTIONARY ADT operations can be implemented in Q(1) time. Of course, this strategy relies on proper selection of the hash function. An ordinary hash function h performs a mapping from the universe of keys U to slots in the hash table T [0,, m 1]: h : U fi [0, 1,..., m 1] Since U is generally much larger than m, h is unlikely to perform a one-toone mapping. In other words, it is very probable that: for two keys k i and k j, where i j, h(k i ) = h(k j ). This situation, where two different keys hash to the same slot, is referred to as a collision. Since two elements cannot be stored in the same slot in a hash table, the Insert operation must resolve collisions by relocating an element so that it can be found by subsequent Search and Delete operations. This will increase the running time of all three operations. There is an interesting space-time trade-off associated with hash tables. By making the table size m larger, the chances of collisions are generally reduced. However, if m is too large most of the hash table slots will never be utilized. In general, m should be proportional to n, the number of elements that must be stored in the hash table. If we let α denote the load factor of a hash table (i.e., the ratio of the number of elements currently stored in the table, to the size of the table), then a rule of thumb that works well in practice is: to choose m so that a never exceeds 0.8 while using the hash table
18 The development of efficient strategies for resolving collisions is an important issue. But the issues related to the design of "good" hash functions, and various methods for creating them are important too. Extendible Hashing Extendible hashing limits the overhead due to rehashing by splitting the hash table into blocks. The hashing process then proceeds in two steps: The low-order bits of a key are first checked to determine which block a data element will be stored in (i.e., all data elements in a given block will have identical low-order bits), and then the data element is actually hashed into a particular slot in that block using the methods discussed. The addresses of these blocks are stored in a directory table. In addition, a value b is stored with the table - this gives the number of low-order bits to use during the first step of the hashing process. Table overflow can now be handled as follows. Whenever the load factor a, of any one block d is exceeded, an additional block d' the same size as d is created, and the elements originally in d are rehashed into both d and d' using b + 1 low-order bits in the first step of the hashing process. Of course, the size of the directory table must be doubled at this point, since the value of b is increased by one. This process is demonstrated in figure above. Extendible hashing, if applied to disk memory, gives an alternative to B-trees. This method involves two disk accesses for each search in typical applications while at the same time allowing efficient insertion. The records are stored on pages (clusters) which are split into two pieces when they fill up. The example, for the string of input data: E X T E R N A L S E A R C H I N G E X A M P L E
19 The first page Directory split First page again full Second split
20 Third split Fourth split
21 Extendible hashing access Property: With pages that can hold M records, extendible hashing may be expected to require about 1.44 ( N / M ) pages for a file of N records. The directory may be expected to have about N 1+1/M / M entries. The analysis of algorithm is complicated and beyond the scope of material.
Hashing. Hashing Procedures
 Hashing Hashing Procedures Let us denote the set of all possible key values (i.e., the universe of keys) used in a dictionary application by U. Suppose an application requires a dictionary in which elements
Hashing Hashing Procedures Let us denote the set of all possible key values (i.e., the universe of keys) used in a dictionary application by U. Suppose an application requires a dictionary in which elements
Data Partitioning. Figure 1-31: Communication Topologies. Regular Partitions
 Data In single-program multiple-data (SPMD) parallel programs, global data is partitioned, with a portion of the data assigned to each processing node. Issues relevant to choosing a partitioning strategy
Data In single-program multiple-data (SPMD) parallel programs, global data is partitioned, with a portion of the data assigned to each processing node. Issues relevant to choosing a partitioning strategy
SHAPE AND STRUCTURE. Shape and Structure. An explanation of Mathematical terminology
 Shape and Structure An explanation of Mathematical terminology 2005 1 POINT A dot Dots join to make lines LINE A line is 1 dimensional (length) A line is a series of points touching each other and extending
Shape and Structure An explanation of Mathematical terminology 2005 1 POINT A dot Dots join to make lines LINE A line is 1 dimensional (length) A line is a series of points touching each other and extending
17/07/2013 RASTER DATA STRUCTURE GIS LECTURE 4 GIS DATA MODELS AND STRUCTURES RASTER DATA MODEL& STRUCTURE TIN- TRIANGULAR IRREGULAR NETWORK
 RASTER DATA STRUCTURE GIS LECTURE 4 GIS DATA MODELS AND STRUCTURES Space is subdivided into regular grids of square grid cells or other forms of polygonal meshes known as picture elements (pixels) the
RASTER DATA STRUCTURE GIS LECTURE 4 GIS DATA MODELS AND STRUCTURES Space is subdivided into regular grids of square grid cells or other forms of polygonal meshes known as picture elements (pixels) the
Class #2. Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures
 Class #2 Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures Role of a Data Model Levels of Data Model Abstraction GIS as Digital
Class #2 Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures Role of a Data Model Levels of Data Model Abstraction GIS as Digital
Geometry Vocabulary. acute angle-an angle measuring less than 90 degrees
 Geometry Vocabulary acute angle-an angle measuring less than 90 degrees angle-the turn or bend between two intersecting lines, line segments, rays, or planes angle bisector-an angle bisector is a ray that
Geometry Vocabulary acute angle-an angle measuring less than 90 degrees angle-the turn or bend between two intersecting lines, line segments, rays, or planes angle bisector-an angle bisector is a ray that
The National Strategies Secondary Mathematics exemplification: Y8, 9
 Mathematics exemplification: Y8, 9 183 As outcomes, Year 8 pupils should, for example: Understand a proof that the sum of the angles of a triangle is 180 and of a quadrilateral is 360, and that the exterior
Mathematics exemplification: Y8, 9 183 As outcomes, Year 8 pupils should, for example: Understand a proof that the sum of the angles of a triangle is 180 and of a quadrilateral is 360, and that the exterior
DATA MODELS IN GIS. Prachi Misra Sahoo I.A.S.R.I., New Delhi
 DATA MODELS IN GIS Prachi Misra Sahoo I.A.S.R.I., New Delhi -110012 1. Introduction GIS depicts the real world through models involving geometry, attributes, relations, and data quality. Here the realization
DATA MODELS IN GIS Prachi Misra Sahoo I.A.S.R.I., New Delhi -110012 1. Introduction GIS depicts the real world through models involving geometry, attributes, relations, and data quality. Here the realization
Number/Computation. addend Any number being added. digit Any one of the ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9
 14 Number/Computation addend Any number being added algorithm A step-by-step method for computing array A picture that shows a number of items arranged in rows and columns to form a rectangle associative
14 Number/Computation addend Any number being added algorithm A step-by-step method for computing array A picture that shows a number of items arranged in rows and columns to form a rectangle associative
Fractals: a way to represent natural objects
 Fractals: a way to represent natural objects In spatial information systems there are two kinds of entity to model: natural earth features like terrain and coastlines; human-made objects like buildings
Fractals: a way to represent natural objects In spatial information systems there are two kinds of entity to model: natural earth features like terrain and coastlines; human-made objects like buildings
Course Number: Course Title: Geometry
 Course Number: 1206310 Course Title: Geometry RELATED GLOSSARY TERM DEFINITIONS (89) Altitude The perpendicular distance from the top of a geometric figure to its opposite side. Angle Two rays or two line
Course Number: 1206310 Course Title: Geometry RELATED GLOSSARY TERM DEFINITIONS (89) Altitude The perpendicular distance from the top of a geometric figure to its opposite side. Angle Two rays or two line
absolute value- the absolute value of a number is the distance between that number and 0 on a number line. Absolute value is shown 7 = 7-16 = 16
 Grade Six MATH GLOSSARY absolute value- the absolute value of a number is the distance between that number and 0 on a number line. Absolute value is shown 7 = 7-16 = 16 abundant number: A number whose
Grade Six MATH GLOSSARY absolute value- the absolute value of a number is the distance between that number and 0 on a number line. Absolute value is shown 7 = 7-16 = 16 abundant number: A number whose
CS 465 Program 4: Modeller
 CS 465 Program 4: Modeller out: 30 October 2004 due: 16 November 2004 1 Introduction In this assignment you will work on a simple 3D modelling system that uses simple primitives and curved surfaces organized
CS 465 Program 4: Modeller out: 30 October 2004 due: 16 November 2004 1 Introduction In this assignment you will work on a simple 3D modelling system that uses simple primitives and curved surfaces organized
coding of various parts showing different features, the possibility of rotation or of hiding covering parts of the object's surface to gain an insight
 Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Curriki Geometry Glossary
 Curriki Geometry Glossary The following terms are used throughout the Curriki Geometry projects and represent the core vocabulary and concepts that students should know to meet Common Core State Standards.
Curriki Geometry Glossary The following terms are used throughout the Curriki Geometry projects and represent the core vocabulary and concepts that students should know to meet Common Core State Standards.
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling Welcome to the lectures on computer graphics. We have
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling Welcome to the lectures on computer graphics. We have
Multidimensional Data and Modelling
 Multidimensional Data and Modelling 1 Problems of multidimensional data structures l multidimensional (md-data or spatial) data and their implementation of operations between objects (spatial data practically
Multidimensional Data and Modelling 1 Problems of multidimensional data structures l multidimensional (md-data or spatial) data and their implementation of operations between objects (spatial data practically
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into
 2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
Lecture 17: Solid Modeling.... a cubit on the one side, and a cubit on the other side Exodus 26:13
 Lecture 17: Solid Modeling... a cubit on the one side, and a cubit on the other side Exodus 26:13 Who is on the LORD's side? Exodus 32:26 1. Solid Representations A solid is a 3-dimensional shape with
Lecture 17: Solid Modeling... a cubit on the one side, and a cubit on the other side Exodus 26:13 Who is on the LORD's side? Exodus 32:26 1. Solid Representations A solid is a 3-dimensional shape with
Geographic Information Fundamentals Overview
 CEN TC 287 Date: 1998-07 CR 287002:1998 CEN TC 287 Secretariat: AFNOR Geographic Information Fundamentals Overview Geoinformation Übersicht Information géographique Vue d'ensemble ICS: Descriptors: Document
CEN TC 287 Date: 1998-07 CR 287002:1998 CEN TC 287 Secretariat: AFNOR Geographic Information Fundamentals Overview Geoinformation Übersicht Information géographique Vue d'ensemble ICS: Descriptors: Document
Unit 1, Lesson 1: Moving in the Plane
 Unit 1, Lesson 1: Moving in the Plane Let s describe ways figures can move in the plane. 1.1: Which One Doesn t Belong: Diagrams Which one doesn t belong? 1.2: Triangle Square Dance m.openup.org/1/8-1-1-2
Unit 1, Lesson 1: Moving in the Plane Let s describe ways figures can move in the plane. 1.1: Which One Doesn t Belong: Diagrams Which one doesn t belong? 1.2: Triangle Square Dance m.openup.org/1/8-1-1-2
Prime Time (Factors and Multiples)
 CONFIDENCE LEVEL: Prime Time Knowledge Map for 6 th Grade Math Prime Time (Factors and Multiples). A factor is a whole numbers that is multiplied by another whole number to get a product. (Ex: x 5 = ;
CONFIDENCE LEVEL: Prime Time Knowledge Map for 6 th Grade Math Prime Time (Factors and Multiples). A factor is a whole numbers that is multiplied by another whole number to get a product. (Ex: x 5 = ;
Introduction to Geographic Information Science. Some Updates. Last Lecture 4/6/2017. Geography 4103 / Raster Data and Tesselations.
 Geography 43 / 3 Introduction to Geographic Information Science Raster Data and Tesselations Schedule Some Updates Last Lecture We finished DBMS and learned about storage of data in complex databases Relational
Geography 43 / 3 Introduction to Geographic Information Science Raster Data and Tesselations Schedule Some Updates Last Lecture We finished DBMS and learned about storage of data in complex databases Relational
MATH DICTIONARY. Number Sense. Number Families. Operations. Counting (Natural) Numbers The numbers we say when we count. Example: {0, 1, 2, 3, 4 }
 Number Sense Number Families MATH DICTIONARY Counting (Natural) Numbers The numbers we say when we count Example: {1, 2, 3, 4 } Whole Numbers The counting numbers plus zero Example: {0, 1, 2, 3, 4 } Positive
Number Sense Number Families MATH DICTIONARY Counting (Natural) Numbers The numbers we say when we count Example: {1, 2, 3, 4 } Whole Numbers The counting numbers plus zero Example: {0, 1, 2, 3, 4 } Positive
The Ultimate Maths Vocabulary List
 The Ultimate Maths Vocabulary List The 96 Words Every Pupil Needs to Know by the End of Year 6 KS1 & KS2 How to Use This Resource An essential building block in pupil s understanding of maths is their
The Ultimate Maths Vocabulary List The 96 Words Every Pupil Needs to Know by the End of Year 6 KS1 & KS2 How to Use This Resource An essential building block in pupil s understanding of maths is their
Glossary of dictionary terms in the AP geometry units
 Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Curriculum Connections (Fractions): K-8 found at under Planning Supports
 Curriculum Connections (Fractions): K-8 found at http://www.edugains.ca/newsite/digitalpapers/fractions/resources.html under Planning Supports Kindergarten Grade 1 Grade 2 Grade 3 Grade 4 Grade 5 Grade
Curriculum Connections (Fractions): K-8 found at http://www.edugains.ca/newsite/digitalpapers/fractions/resources.html under Planning Supports Kindergarten Grade 1 Grade 2 Grade 3 Grade 4 Grade 5 Grade
Answer Key: Three-Dimensional Cross Sections
 Geometry A Unit Answer Key: Three-Dimensional Cross Sections Name Date Objectives In this lesson, you will: visualize three-dimensional objects from different perspectives be able to create a projection
Geometry A Unit Answer Key: Three-Dimensional Cross Sections Name Date Objectives In this lesson, you will: visualize three-dimensional objects from different perspectives be able to create a projection
CAR-TR-990 CS-TR-4526 UMIACS September 2003
 CAR-TR-990 CS-TR-4526 UMIACS 2003-94 September 2003 Object-based and Image-based Object Representations Hanan Samet Computer Science Department Center for Automation Research Institute for Advanced Computer
CAR-TR-990 CS-TR-4526 UMIACS 2003-94 September 2003 Object-based and Image-based Object Representations Hanan Samet Computer Science Department Center for Automation Research Institute for Advanced Computer
Representing Geography
 Data models and axioms Chapters 3 and 7 Representing Geography Road map Representing the real world Conceptual models: objects vs fields Implementation models: vector vs raster Vector topological model
Data models and axioms Chapters 3 and 7 Representing Geography Road map Representing the real world Conceptual models: objects vs fields Implementation models: vector vs raster Vector topological model
A triangle that has three acute angles Example:
 1. acute angle : An angle that measures less than a right angle (90 ). 2. acute triangle : A triangle that has three acute angles 3. angle : A figure formed by two rays that meet at a common endpoint 4.
1. acute angle : An angle that measures less than a right angle (90 ). 2. acute triangle : A triangle that has three acute angles 3. angle : A figure formed by two rays that meet at a common endpoint 4.
(Refer Slide Time: 00:02:00)
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 18 Polyfill - Scan Conversion of a Polygon Today we will discuss the concepts
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 18 Polyfill - Scan Conversion of a Polygon Today we will discuss the concepts
Mathematics K-8 Content Standards
 Mathematics K-8 Content Standards Kindergarten K.1 Number and Operations and Algebra: Represent, compare, and order whole numbers, and join and separate sets. K.1.1 Read and write whole numbers to 10.
Mathematics K-8 Content Standards Kindergarten K.1 Number and Operations and Algebra: Represent, compare, and order whole numbers, and join and separate sets. K.1.1 Read and write whole numbers to 10.
Spatial Data Models. Raster uses individual cells in a matrix, or grid, format to represent real world entities
 Spatial Data Models Raster uses individual cells in a matrix, or grid, format to represent real world entities Vector uses coordinates to store the shape of spatial data objects David Tenenbaum GEOG 7
Spatial Data Models Raster uses individual cells in a matrix, or grid, format to represent real world entities Vector uses coordinates to store the shape of spatial data objects David Tenenbaum GEOG 7
7 Fractions. Number Sense and Numeration Measurement Geometry and Spatial Sense Patterning and Algebra Data Management and Probability
 7 Fractions GRADE 7 FRACTIONS continue to develop proficiency by using fractions in mental strategies and in selecting and justifying use; develop proficiency in adding and subtracting simple fractions;
7 Fractions GRADE 7 FRACTIONS continue to develop proficiency by using fractions in mental strategies and in selecting and justifying use; develop proficiency in adding and subtracting simple fractions;
Main Idea: classify polygons and determine which polygons can form a tessellation.
 10 8: Polygons and Tesselations Main Idea: classify polygons and determine which polygons can form a tessellation. Vocabulary: polygon A simple closed figure in a plane formed by three or more line segments
10 8: Polygons and Tesselations Main Idea: classify polygons and determine which polygons can form a tessellation. Vocabulary: polygon A simple closed figure in a plane formed by three or more line segments
L1 - Introduction. Contents. Introduction of CAD/CAM system Components of CAD/CAM systems Basic concepts of graphics programming
 L1 - Introduction Contents Introduction of CAD/CAM system Components of CAD/CAM systems Basic concepts of graphics programming 1 Definitions Computer-Aided Design (CAD) The technology concerned with the
L1 - Introduction Contents Introduction of CAD/CAM system Components of CAD/CAM systems Basic concepts of graphics programming 1 Definitions Computer-Aided Design (CAD) The technology concerned with the
INSTRUCTIONS FOR THE USE OF THE SUPER RULE TM
 INSTRUCTIONS FOR THE USE OF THE SUPER RULE TM NOTE: All images in this booklet are scale drawings only of template shapes and scales. Preparation: Your SUPER RULE TM is a valuable acquisition for classroom
INSTRUCTIONS FOR THE USE OF THE SUPER RULE TM NOTE: All images in this booklet are scale drawings only of template shapes and scales. Preparation: Your SUPER RULE TM is a valuable acquisition for classroom
Understanding Geospatial Data Models
 Understanding Geospatial Data Models 1 A geospatial data model is a formal means of representing spatially referenced information. It is a simplified view of physical entities and a conceptualization of
Understanding Geospatial Data Models 1 A geospatial data model is a formal means of representing spatially referenced information. It is a simplified view of physical entities and a conceptualization of
Geometry Foundations Planning Document
 Geometry Foundations Planning Document Unit 1: Chromatic Numbers Unit Overview A variety of topics allows students to begin the year successfully, review basic fundamentals, develop cooperative learning
Geometry Foundations Planning Document Unit 1: Chromatic Numbers Unit Overview A variety of topics allows students to begin the year successfully, review basic fundamentals, develop cooperative learning
CS301 - Data Structures Glossary By
 CS301 - Data Structures Glossary By Abstract Data Type : A set of data values and associated operations that are precisely specified independent of any particular implementation. Also known as ADT Algorithm
CS301 - Data Structures Glossary By Abstract Data Type : A set of data values and associated operations that are precisely specified independent of any particular implementation. Also known as ADT Algorithm
M. Andrea Rodríguez-Tastets. I Semester 2008
 M. -Tastets Universidad de Concepción,Chile andrea@udec.cl I Semester 2008 Outline refers to data with a location on the Earth s surface. Examples Census data Administrative boundaries of a country, state
M. -Tastets Universidad de Concepción,Chile andrea@udec.cl I Semester 2008 Outline refers to data with a location on the Earth s surface. Examples Census data Administrative boundaries of a country, state
Smarter Balanced Vocabulary (from the SBAC test/item specifications)
 Example: Smarter Balanced Vocabulary (from the SBAC test/item specifications) Notes: Most terms area used in multiple grade levels. You should look at your grade level and all of the previous grade levels.
Example: Smarter Balanced Vocabulary (from the SBAC test/item specifications) Notes: Most terms area used in multiple grade levels. You should look at your grade level and all of the previous grade levels.
acute angle An angle with a measure less than that of a right angle. Houghton Mifflin Co. 2 Grade 5 Unit 6
 acute angle An angle with a measure less than that of a right angle. Houghton Mifflin Co. 2 Grade 5 Unit 6 angle An angle is formed by two rays with a common end point. Houghton Mifflin Co. 3 Grade 5 Unit
acute angle An angle with a measure less than that of a right angle. Houghton Mifflin Co. 2 Grade 5 Unit 6 angle An angle is formed by two rays with a common end point. Houghton Mifflin Co. 3 Grade 5 Unit
TIPS4Math Grades 4 to 6 Overview Grade 4 Grade 5 Grade 6 Collect, Organize, and Display Primary Data (4+ days)
 Collect, Organize, and Display Primary Data (4+ days) Collect, Organize, Display and Interpret Categorical Data (5+ days) 4m88 Collect data by conducting a survey or an experiment to do with the 4m89 Collect
Collect, Organize, and Display Primary Data (4+ days) Collect, Organize, Display and Interpret Categorical Data (5+ days) 4m88 Collect data by conducting a survey or an experiment to do with the 4m89 Collect
Selective Space Structures Manual
 Selective Space Structures Manual February 2017 CONTENTS 1 Contents 1 Overview and Concept 4 1.1 General Concept........................... 4 1.2 Modules................................ 6 2 The 3S Generator
Selective Space Structures Manual February 2017 CONTENTS 1 Contents 1 Overview and Concept 4 1.1 General Concept........................... 4 1.2 Modules................................ 6 2 The 3S Generator
CMSC 425: Lecture 10 Geometric Data Structures for Games: Index Structures Tuesday, Feb 26, 2013
 CMSC 2: Lecture 10 Geometric Data Structures for Games: Index Structures Tuesday, Feb 2, 201 Reading: Some of today s materials can be found in Foundations of Multidimensional and Metric Data Structures,
CMSC 2: Lecture 10 Geometric Data Structures for Games: Index Structures Tuesday, Feb 2, 201 Reading: Some of today s materials can be found in Foundations of Multidimensional and Metric Data Structures,
Chapter 11: Indexing and Hashing
 Chapter 11: Indexing and Hashing Basic Concepts Ordered Indices B + -Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing and Hashing Index Definition in SQL
Chapter 11: Indexing and Hashing Basic Concepts Ordered Indices B + -Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing and Hashing Index Definition in SQL
TOURNAMENT OF THE TOWNS, Glossary
 TOURNAMENT OF THE TOWNS, 2003 2004 Glossary Absolute value The size of a number with its + or sign removed. The absolute value of 3.2 is 3.2, the absolute value of +4.6 is 4.6. We write this: 3.2 = 3.2
TOURNAMENT OF THE TOWNS, 2003 2004 Glossary Absolute value The size of a number with its + or sign removed. The absolute value of 3.2 is 3.2, the absolute value of +4.6 is 4.6. We write this: 3.2 = 3.2
Solids as point set. Solid models. Solid representation schemes (cont d) Solid representation schemes. Solid representation schemes (cont d)
 Solid models Solid models developed to address limitations of wireframe modeling. Attempt was to create systems which create only complete representations. Modelers would support direct creation of 3D
Solid models Solid models developed to address limitations of wireframe modeling. Attempt was to create systems which create only complete representations. Modelers would support direct creation of 3D
3.Data Abstraction. Prof. Tulasi Prasad Sariki SCSE, VIT, Chennai 1 / 26
 3.Data Abstraction Prof. Tulasi Prasad Sariki SCSE, VIT, Chennai www.learnersdesk.weebly.com 1 / 26 Outline What can be visualized? Why Do Data Semantics and Types Matter? Data Types Items, Attributes,
3.Data Abstraction Prof. Tulasi Prasad Sariki SCSE, VIT, Chennai www.learnersdesk.weebly.com 1 / 26 Outline What can be visualized? Why Do Data Semantics and Types Matter? Data Types Items, Attributes,
Longley Chapter 3. Representations
 Longley Chapter 3 Digital Geographic Data Representation Geographic Data Type Data Models Representing Spatial and Temporal Data Attributes The Nature of Geographic Data Representations Are needed to convey
Longley Chapter 3 Digital Geographic Data Representation Geographic Data Type Data Models Representing Spatial and Temporal Data Attributes The Nature of Geographic Data Representations Are needed to convey
Grade 9 Math Terminology
 Unit 1 Basic Skills Review BEDMAS a way of remembering order of operations: Brackets, Exponents, Division, Multiplication, Addition, Subtraction Collect like terms gather all like terms and simplify as
Unit 1 Basic Skills Review BEDMAS a way of remembering order of operations: Brackets, Exponents, Division, Multiplication, Addition, Subtraction Collect like terms gather all like terms and simplify as
Scope and Sequence for the New Jersey Core Curriculum Content Standards
 Scope and Sequence for the New Jersey Core Curriculum Content Standards The following chart provides an overview of where within Prentice Hall Course 3 Mathematics each of the Cumulative Progress Indicators
Scope and Sequence for the New Jersey Core Curriculum Content Standards The following chart provides an overview of where within Prentice Hall Course 3 Mathematics each of the Cumulative Progress Indicators
Chapter 12: Indexing and Hashing. Basic Concepts
 Chapter 12: Indexing and Hashing! Basic Concepts! Ordered Indices! B+-Tree Index Files! B-Tree Index Files! Static Hashing! Dynamic Hashing! Comparison of Ordered Indexing and Hashing! Index Definition
Chapter 12: Indexing and Hashing! Basic Concepts! Ordered Indices! B+-Tree Index Files! B-Tree Index Files! Static Hashing! Dynamic Hashing! Comparison of Ordered Indexing and Hashing! Index Definition
Ray Tracing Acceleration Data Structures
 Ray Tracing Acceleration Data Structures Sumair Ahmed October 29, 2009 Ray Tracing is very time-consuming because of the ray-object intersection calculations. With the brute force method, each ray has
Ray Tracing Acceleration Data Structures Sumair Ahmed October 29, 2009 Ray Tracing is very time-consuming because of the ray-object intersection calculations. With the brute force method, each ray has
Advances in Data Management Principles of Database Systems - 2 A.Poulovassilis
 1 Advances in Data Management Principles of Database Systems - 2 A.Poulovassilis 1 Storing data on disk The traditional storage hierarchy for DBMSs is: 1. main memory (primary storage) for data currently
1 Advances in Data Management Principles of Database Systems - 2 A.Poulovassilis 1 Storing data on disk The traditional storage hierarchy for DBMSs is: 1. main memory (primary storage) for data currently
Key Question. Focus. What are the geometric properties of a regular tetrahedron, and how do these compare to a bird tetrahedron?
 Key Question What are the geometric properties of a regular tetrahedron, and how do these compare to a bird tetrahedron? Math Properties of polyhedra faces edges vertices Surface area Integrated Processes
Key Question What are the geometric properties of a regular tetrahedron, and how do these compare to a bird tetrahedron? Math Properties of polyhedra faces edges vertices Surface area Integrated Processes
Interactive Math Glossary Terms and Definitions
 Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Mathematics Curriculum
 6 G R A D E Mathematics Curriculum GRADE 6 5 Table of Contents 1... 1 Topic A: Area of Triangles, Quadrilaterals, and Polygons (6.G.A.1)... 11 Lesson 1: The Area of Parallelograms Through Rectangle Facts...
6 G R A D E Mathematics Curriculum GRADE 6 5 Table of Contents 1... 1 Topic A: Area of Triangles, Quadrilaterals, and Polygons (6.G.A.1)... 11 Lesson 1: The Area of Parallelograms Through Rectangle Facts...
Maps as Numbers: Data Models
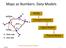 Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
Solid Modelling. Graphics Systems / Computer Graphics and Interfaces COLLEGE OF ENGINEERING UNIVERSITY OF PORTO
 Solid Modelling Graphics Systems / Computer Graphics and Interfaces 1 Solid Modelling In 2D, one set 2D line segments or curves does not necessarily form a closed area. In 3D, a collection of surfaces
Solid Modelling Graphics Systems / Computer Graphics and Interfaces 1 Solid Modelling In 2D, one set 2D line segments or curves does not necessarily form a closed area. In 3D, a collection of surfaces
The Game of Criss-Cross
 Chapter 5 The Game of Criss-Cross Euler Characteristic ( ) Overview. The regions on a map and the faces of a cube both illustrate a very natural sort of situation: they are each examples of regions that
Chapter 5 The Game of Criss-Cross Euler Characteristic ( ) Overview. The regions on a map and the faces of a cube both illustrate a very natural sort of situation: they are each examples of regions that
Chapter 12: Indexing and Hashing
 Chapter 12: Indexing and Hashing Basic Concepts Ordered Indices B+-Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing and Hashing Index Definition in SQL
Chapter 12: Indexing and Hashing Basic Concepts Ordered Indices B+-Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing and Hashing Index Definition in SQL
3 Polygonal Modeling. Getting Started with Maya 103
 3 Polygonal Modeling In Maya, modeling refers to the process of creating virtual 3D surfaces for the characters and objects in the Maya scene. Surfaces play an important role in the overall Maya workflow
3 Polygonal Modeling In Maya, modeling refers to the process of creating virtual 3D surfaces for the characters and objects in the Maya scene. Surfaces play an important role in the overall Maya workflow
Intersection Acceleration
 Advanced Computer Graphics Intersection Acceleration Matthias Teschner Computer Science Department University of Freiburg Outline introduction bounding volume hierarchies uniform grids kd-trees octrees
Advanced Computer Graphics Intersection Acceleration Matthias Teschner Computer Science Department University of Freiburg Outline introduction bounding volume hierarchies uniform grids kd-trees octrees
Alaska Mathematics Standards Vocabulary Word List Grade 7
 1 estimate proportion proportional relationship rate ratio rational coefficient rational number scale Ratios and Proportional Relationships To find a number close to an exact amount; an estimate tells
1 estimate proportion proportional relationship rate ratio rational coefficient rational number scale Ratios and Proportional Relationships To find a number close to an exact amount; an estimate tells
Introduction :- Storage of GIS Database :- What is tiling?
 Introduction :- GIS storage and editing subsystems provides a variety of tools for storing and maintaining the digital representation of a study area. It also provide tools for examining each theme for
Introduction :- GIS storage and editing subsystems provides a variety of tools for storing and maintaining the digital representation of a study area. It also provide tools for examining each theme for
1. Introduction to Constructive Solid Geometry (CSG)
 opyright@010, YZU Optimal Design Laboratory. All rights reserved. Last updated: Yeh-Liang Hsu (010-1-10). Note: This is the course material for ME550 Geometric modeling and computer graphics, Yuan Ze University.
opyright@010, YZU Optimal Design Laboratory. All rights reserved. Last updated: Yeh-Liang Hsu (010-1-10). Note: This is the course material for ME550 Geometric modeling and computer graphics, Yuan Ze University.
A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3
 A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3 ANDREW J. HANSON AND JI-PING SHA In this paper we present a systematic and explicit algorithm for tessellating the algebraic surfaces (real 4-manifolds) F
A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3 ANDREW J. HANSON AND JI-PING SHA In this paper we present a systematic and explicit algorithm for tessellating the algebraic surfaces (real 4-manifolds) F
Lecture 6: GIS Spatial Analysis. GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University
 Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
Unit 1, Lesson 1: Tiling the Plane
 Unit 1, Lesson 1: Tiling the Plane Let s look at tiling patterns and think about area. 1.1: Which One Doesn t Belong: Tilings Which pattern doesn t belong? 1 1.2: More Red, Green, or Blue? m.openup.org//6-1-1-2
Unit 1, Lesson 1: Tiling the Plane Let s look at tiling patterns and think about area. 1.1: Which One Doesn t Belong: Tilings Which pattern doesn t belong? 1 1.2: More Red, Green, or Blue? m.openup.org//6-1-1-2
Maths Scope and Sequence. Gr. 5 - Data Handling. Mathematics Scope and Sequence Document Last Updated August SM
 Maths Scope and Sequence Mathematics Scope and Sequence Document Last Updated ugust 2013. SM Gr. 5 - Data Handling Overall expectation - Phase 4 Learners will collect, organize and display data for the
Maths Scope and Sequence Mathematics Scope and Sequence Document Last Updated ugust 2013. SM Gr. 5 - Data Handling Overall expectation - Phase 4 Learners will collect, organize and display data for the
YEAR 7 SCHEME OF WORK - EXTENSION
 YEAR 7 SCHEME OF WORK - EXTENSION Autumn Term 1 Number Skills Spring Term 1 Angles and Shape Summer Term 1 Multiplicative Reasoning Analysing and displaying data Decimals Perimeter, Area and Volume Half
YEAR 7 SCHEME OF WORK - EXTENSION Autumn Term 1 Number Skills Spring Term 1 Angles and Shape Summer Term 1 Multiplicative Reasoning Analysing and displaying data Decimals Perimeter, Area and Volume Half
1 The range query problem
 CS268: Geometric Algorithms Handout #12 Design and Analysis Original Handout #12 Stanford University Thursday, 19 May 1994 Original Lecture #12: Thursday, May 19, 1994 Topics: Range Searching with Partition
CS268: Geometric Algorithms Handout #12 Design and Analysis Original Handout #12 Stanford University Thursday, 19 May 1994 Original Lecture #12: Thursday, May 19, 1994 Topics: Range Searching with Partition
Tips for a Good Meshing Experience
 Tips for a Good Meshing Experience Meshes are very powerful and flexible for modeling 2D overland flows in a complex urban environment. However, complex geometries can be frustrating for many modelers
Tips for a Good Meshing Experience Meshes are very powerful and flexible for modeling 2D overland flows in a complex urban environment. However, complex geometries can be frustrating for many modelers
Data Representation in Visualisation
 Data Representation in Visualisation Visualisation Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Data Representation We have
Data Representation in Visualisation Visualisation Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Data Representation We have
3. MODELING A THREE-PIPE INTERSECTION (3-D)
 3. MODELING A THREE-PIPE INTERSECTION (3-D) This tutorial employs primitives that is, predefined GAMBIT modeling components and procedures. There are two types of GAMBIT primitives: Geometry Mesh Geometry
3. MODELING A THREE-PIPE INTERSECTION (3-D) This tutorial employs primitives that is, predefined GAMBIT modeling components and procedures. There are two types of GAMBIT primitives: Geometry Mesh Geometry
CTI, November 19, 2015
 Consider a large cube made from unit cubes 1 Suppose our cube is n n n Look at the cube from a corner so that you can see three faces How many unit cubes are in your line of vision? Build a table that
Consider a large cube made from unit cubes 1 Suppose our cube is n n n Look at the cube from a corner so that you can see three faces How many unit cubes are in your line of vision? Build a table that
EAT 233/3 GEOGRAPHIC INFORMATION SYSTEM (GIS)
 EAT 233/3 GEOGRAPHIC INFORMATION SYSTEM (GIS) CO3: Ability to produce detail mapping using geographic information systems (GIS) BY : AYU WAZIRA AZHARI SPATIAL DATA & THE MODELLING Spatial Data in GIS Spatial
EAT 233/3 GEOGRAPHIC INFORMATION SYSTEM (GIS) CO3: Ability to produce detail mapping using geographic information systems (GIS) BY : AYU WAZIRA AZHARI SPATIAL DATA & THE MODELLING Spatial Data in GIS Spatial
GEOMETRIC TOOLS FOR COMPUTER GRAPHICS
 GEOMETRIC TOOLS FOR COMPUTER GRAPHICS PHILIP J. SCHNEIDER DAVID H. EBERLY MORGAN KAUFMANN PUBLISHERS A N I M P R I N T O F E L S E V I E R S C I E N C E A M S T E R D A M B O S T O N L O N D O N N E W
GEOMETRIC TOOLS FOR COMPUTER GRAPHICS PHILIP J. SCHNEIDER DAVID H. EBERLY MORGAN KAUFMANN PUBLISHERS A N I M P R I N T O F E L S E V I E R S C I E N C E A M S T E R D A M B O S T O N L O N D O N N E W
Crystal Structure. A(r) = A(r + T), (1)
 Crystal Structure In general, by solid we mean an equilibrium state with broken translational symmetry. That is a state for which there exist observables say, densities of particles with spatially dependent
Crystal Structure In general, by solid we mean an equilibrium state with broken translational symmetry. That is a state for which there exist observables say, densities of particles with spatially dependent
Geometry Practice. 1. Angles located next to one another sharing a common side are called angles.
 Geometry Practice Name 1. Angles located next to one another sharing a common side are called angles. 2. Planes that meet to form right angles are called planes. 3. Lines that cross are called lines. 4.
Geometry Practice Name 1. Angles located next to one another sharing a common side are called angles. 2. Planes that meet to form right angles are called planes. 3. Lines that cross are called lines. 4.
layers in a raster model
 layers in a raster model Layer 1 Layer 2 layers in an vector-based model (1) Layer 2 Layer 1 layers in an vector-based model (2) raster versus vector data model Raster model Vector model Simple data structure
layers in a raster model Layer 1 Layer 2 layers in an vector-based model (1) Layer 2 Layer 1 layers in an vector-based model (2) raster versus vector data model Raster model Vector model Simple data structure
Basic Idea. The routing problem is typically solved using a twostep
 Global Routing Basic Idea The routing problem is typically solved using a twostep approach: Global Routing Define the routing regions. Generate a tentative route for each net. Each net is assigned to a
Global Routing Basic Idea The routing problem is typically solved using a twostep approach: Global Routing Define the routing regions. Generate a tentative route for each net. Each net is assigned to a
Aston Hall s A-Z of mathematical terms
 Aston Hall s A-Z of mathematical terms The following guide is a glossary of mathematical terms, covering the concepts children are taught in FS2, KS1 and KS2. This may be useful to clear up any homework
Aston Hall s A-Z of mathematical terms The following guide is a glossary of mathematical terms, covering the concepts children are taught in FS2, KS1 and KS2. This may be useful to clear up any homework
Indices in Information Systems
 Indices in Information Systems Algimantas Juozapavičius algimantas.juozapavicius@maf.vu.lt Data structures and indices are well-known in traditional (textual or numerical) database systems, as well as
Indices in Information Systems Algimantas Juozapavičius algimantas.juozapavicius@maf.vu.lt Data structures and indices are well-known in traditional (textual or numerical) database systems, as well as
Representing the Real World
 Representing the Real World The theory of representing the real world in a GIS using digital data The nature of digital data and binary notation The discrete object view of the world Entities, data objects,
Representing the Real World The theory of representing the real world in a GIS using digital data The nature of digital data and binary notation The discrete object view of the world Entities, data objects,
Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations
 Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations Emma Twersky May 2017 Abstract This paper is an exploration into centroidal Voronoi tessellations, or CVTs. A centroidal
Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations Emma Twersky May 2017 Abstract This paper is an exploration into centroidal Voronoi tessellations, or CVTs. A centroidal
v Overview SMS Tutorials Prerequisites Requirements Time Objectives
 v. 12.2 SMS 12.2 Tutorial Overview Objectives This tutorial describes the major components of the SMS interface and gives a brief introduction to the different SMS modules. Ideally, this tutorial should
v. 12.2 SMS 12.2 Tutorial Overview Objectives This tutorial describes the major components of the SMS interface and gives a brief introduction to the different SMS modules. Ideally, this tutorial should
Prentice Hall Mathematics: Pre-Algebra 2004 Correlated to: Colorado Model Content Standards and Grade Level Expectations (Grade 8)
 Colorado Model Content Standards and Grade Level Expectations (Grade 8) Standard 1: Students develop number sense and use numbers and number relationships in problemsolving situations and communicate the
Colorado Model Content Standards and Grade Level Expectations (Grade 8) Standard 1: Students develop number sense and use numbers and number relationships in problemsolving situations and communicate the
Multidimensional Data and Modelling - DBMS
 Multidimensional Data and Modelling - DBMS 1 DBMS-centric approach Summary: l Spatial data is considered as another type of data beside conventional data in a DBMS. l Enabling advantages of DBMS (data
Multidimensional Data and Modelling - DBMS 1 DBMS-centric approach Summary: l Spatial data is considered as another type of data beside conventional data in a DBMS. l Enabling advantages of DBMS (data
ACT Math test Plane Geometry Review
 Plane geometry problems account for 14 questions on the ACT Math Test that s almost a quarter of the questions on the Subject Test. If you ve taken high school geometry, you ve probably covered all of
Plane geometry problems account for 14 questions on the ACT Math Test that s almost a quarter of the questions on the Subject Test. If you ve taken high school geometry, you ve probably covered all of
Mathematics Background
 Finding Area and Distance Students work in this Unit develops a fundamentally important relationship connecting geometry and algebra: the Pythagorean Theorem. The presentation of ideas in the Unit reflects
Finding Area and Distance Students work in this Unit develops a fundamentally important relationship connecting geometry and algebra: the Pythagorean Theorem. The presentation of ideas in the Unit reflects
Question Bank Subject: Advanced Data Structures Class: SE Computer
 Question Bank Subject: Advanced Data Structures Class: SE Computer Question1: Write a non recursive pseudo code for post order traversal of binary tree Answer: Pseudo Code: 1. Push root into Stack_One.
Question Bank Subject: Advanced Data Structures Class: SE Computer Question1: Write a non recursive pseudo code for post order traversal of binary tree Answer: Pseudo Code: 1. Push root into Stack_One.
In this chapter, we will investigate what have become the standard applications of the integral:
 Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
West Linn-Wilsonville School District Mathematics Curriculum Content Standards Grades K-5. Kindergarten
 Mathematics Curriculum s Kindergarten K.1 Number and Operations and Algebra: Represent, compare, and order whole numbers, and join and separate sets. Read and write whole numbers to 10. Connect numbers,
Mathematics Curriculum s Kindergarten K.1 Number and Operations and Algebra: Represent, compare, and order whole numbers, and join and separate sets. Read and write whole numbers to 10. Connect numbers,
6. Parallel Volume Rendering Algorithms
 6. Parallel Volume Algorithms This chapter introduces a taxonomy of parallel volume rendering algorithms. In the thesis statement we claim that parallel algorithms may be described by "... how the tasks
6. Parallel Volume Algorithms This chapter introduces a taxonomy of parallel volume rendering algorithms. In the thesis statement we claim that parallel algorithms may be described by "... how the tasks
Does it Look Square? Hexagonal Bipyramids, Triangular Antiprismoids, and their Fractals
 Does it Look Square? Hexagonal Bipyramids, Triangular Antiprismoids, and their Fractals Hideki Tsuiki Graduate School of Human and Environmental Studies Kyoto University Yoshida-Nihonmatsu, Kyoto 606-8501,
Does it Look Square? Hexagonal Bipyramids, Triangular Antiprismoids, and their Fractals Hideki Tsuiki Graduate School of Human and Environmental Studies Kyoto University Yoshida-Nihonmatsu, Kyoto 606-8501,
Fractal Gaskets: Reptiles, Hamiltonian Cycles, and Spatial Development
 Bridges Finland Conference Proceedings Fractal Gaskets: Reptiles, Hamiltonian Cycles, and Spatial Development Robert W. Fathauer Tessellations Company 3913 E. Bronco Trail Phoenix, AZ 85044, USA rob@tessellations.com
Bridges Finland Conference Proceedings Fractal Gaskets: Reptiles, Hamiltonian Cycles, and Spatial Development Robert W. Fathauer Tessellations Company 3913 E. Bronco Trail Phoenix, AZ 85044, USA rob@tessellations.com
