Computer Graphics and GPGPU Programming
|
|
|
- Arron Short
- 5 years ago
- Views:
Transcription
1 Computer Graphics and GPGPU Programming Donato D Ambrosio Department of Mathematics and Computer Science and Center of Excellence for High Performace Computing Cubo 22B, University of Calabria, Rende 87036, Italy mailto: donato.dambrosio@unical.it homepage: Academic Year 2018/19 Donato D Ambrosio (University of Calabria) Academic Year 2018/19 1 / 51
2 Table of contents 1 Algorithms Clipping Rasterization Hidden surface removal 2 Light The Phong Model Shading Donato D Ambrosio (University of Calabria) Academic Year 2018/19 2 / 51
3 Algorithms Algorithms Donato D Ambrosio (University of Calabria) Academic Year 2018/19 3 / 51
4 Stages of the OpenGL s Graphics Process The graphics process can be split in the following stages: Modeling (the 3D scene is conceptually defined by means of vertices in a vectorial context) Vertex Processing Primitives (e.g. triangles) are defined Primitives laying outside the clip space are discarded (clipping) Hidden primitives are discarded (hidden surface removal) Rasterization The scene is converted into a raster image (image s elements are called fragments) Fragment processing (a color is assigned to each fragment) Output merging (combine the fragments of all primitives into color pixels for the display) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 4 / 51
5 Clipping Clipping Clipping is the process that discards (entirely or partially) the primitives that are outside the clip space The primitives within the clip space are accepted, while the other are eliminated or rejected The primitives that are partially within the clip space are cut and new vertices added in order to obtain a new primitive that is entirely within the clip space Donato D Ambrosio (University of Calabria) Academic Year 2018/19 5 / 51
6 Clipping Algorithms Clipping Evaluating the intersections with the clip planes is the most important computational effort in clipping algorithm Accordingly, it is important to minimize the number of intersections (since they require floating point operations) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 6 / 51
7 Clipping Cohen-Sutherland s clipping algorithm Let consider the two-dimensional case (it is conceptually equivalent to the three-dimensional one) The edges of the clipping plane are ideally extended to the infinitive by forming 9 regions A 4 bit code O = b 0 b 1 b 2 b 3, called outcode, is assigned to each region Donato D Ambrosio (University of Calabria) Academic Year 2018/19 7 / 51
8 Clipping Cohen-Sutherland s clipping algorithm Outcodes are defined by the following rule: { 1 if y > ymax b 0 = 0 if y y max Similarly, b 1 = 1 if y < y min b 2 and b 3 are defined by relations between x and the left and right edges of the clip region Note that the clip region has outcode O = 0000 Donato D Ambrosio (University of Calabria) Academic Year 2018/19 8 / 51
9 Clipping Cohen-Sutherland s clipping algorithm Case 1: O 1 = O 2 = 0000 Both outcode are The segment is INTERNAL Case 2: O 1 &O The extremes are both up, down, to the left or to the right of the clip window. The segment is EXTERNAL Case 3: O 1 &O 2 = 0000 The extremes are external but the line can not be rejected since it could intersect the window. Intersections with the clip window s edges must be computed and if the line actually intersects the clip region new vertces evaluated Case 4: O ; O 2 = 0000, or viceversa The line is partially outside the clip window. In this case, the vertex outside the window is replaced by a ne vertex resulting from the intersection between the line and the clip window s edge Donato D Ambrosio (University of Calabria) Academic Year 2018/19 9 / 51
10 Rasterization Scan conversion of segments Starting from the vertices of the primitive projected into the two-dimensional plane, the rasterization or scan conversion builds the primitive as a set of fragments Let us suppose the vertices composing the geometric primitives have already been projected on a n m matrix with the origin located at the bottom-left pixel Let us suppose that each pixel is a square with the center at the pixel coordinates and side equal to the distance between two adjacent pixels Donato D Ambrosio (University of Calabria) Academic Year 2018/19 10 / 51
11 The DDA line algorithm Algorithms Rasterization Let us suppose to have a segment defined by its extremes (x 1, y 1 ) and (x 2, y 2 ) The slope of the segment is defined as: m = y/ x The most simple scan conversion algorithm evaluates m, increments x (starting from the left extreme), and computes y i = mx i + h, where h is the ordinata of the intersection between the y axis and the line, for each x i Donato D Ambrosio (University of Calabria) Academic Year 2018/19 11 / 51
12 Rasterization The DDA line algorithm The above strategy is inefficient since each iteration requires one floating point multiplication and one floating point addition It is possible to avoid the multiplication by adopting an incremental strategy so that one pixel can be computed based on the previous one This algorithm is called DDA 1 Each time x is incremented of x, the corresponding variation ofy must be y = m x Ranging form x 1 to x 2, x is incremented by 1 (i.e. the distance between two pixels) and then y is incremented by y = m 1 The name comes from the Digital Differential Analyzer, a mechanical device able to solve differential equations by applying a numerical methods Donato D Ambrosio (University of Calabria) Academic Year 2018/19 12 / 51
13 The DDA line algorithm Algorithms Rasterization Let us assume that 0 m 1 (the other values can be treated equivalently) i n t x ; f l o a t dy, dx, y, m; dy = y2 y1 ; dx = x2 x1 ; m = dy / dx ; y = y1 ; for ( x = x1, x <= x2, x++) { w r i t e P i x e l ( x, round ( y ), l i n e _ c o l o r ) ; y += m; } Donato D Ambrosio (University of Calabria) Academic Year 2018/19 13 / 51
14 Rasterization Bresenham s line algorithm The DDA line algorithm is straightforward and easy to implement but execs a floating point operation for each line s pixel At the contrary, the Bresenham s line algorithm only performs integer operations Bresenham s algorithm is faster than DDA and, for this reason, it has become the most used line algorithm in Computer Graphics *** Let us suppose to have a segment defined by its extremes (x 1, y 1 ) and (x 2, y 2 ) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 14 / 51
15 Rasterization Bresenham s line algorithm Let us suppose we are at an intermediate step of the algorithm and the pixel (i, j) was the last to be switched on As a consequence, when x = i the line y = mx + h intersects the pixel (i, j) When x = i + 1, the condition 0 m 1 implies that only one of the pixels (i + 1, j) and (i + 1, j + 1) can be switched on The choice can be expressed by means of a decision variable d = b a where a and b are the measures of lines starting from the centers of pixels (i + 1, j + 1) and (i + 1, j), respectively (as shown in the next figure), to the line y = mx + h and parallel to the y axis Donato D Ambrosio (University of Calabria) Academic Year 2018/19 15 / 51
16 Rasterization Bresenham s line algorithm Definition of the decision variable d = b a If d > 0 then the line y = mx + h is closest to the pixel (i + 1, j + 1) If d 0 then the line y = mx + h is closest to the pixel (i + 1, j) d can be computed without the need of floating point operations by means of a recurrence formula where d i+1 is a function of d i Donato D Ambrosio (University of Calabria) Academic Year 2018/19 16 / 51
17 Bresenham s line algorithm Rasterization Case d i > b i+1 = b i + m b i+1 = b i + m 1 a i+1 = 1 b i+1 = 1 (b i + m 1) = 1 (1 a i + m 1) = a i m + 1 d i+1 = b i+1 a i+1 = b i a i + 2m 2 = d i + 2m 2 = d i + 2(m 1) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 17 / 51
18 Bresenham s line algorithm Rasterization Case d i 0 b i+1 = b i + m a i+1 = a i m d i+1 = b i+1 a i+1 = b i a i + 2m = d i + 2m Donato D Ambrosio (University of Calabria) Academic Year 2018/19 18 / 51
19 Rasterization Bresenham s line algorithm So, we have d i+1 = { di + 2(m 1) if d > 0 d i + 2m if d 0 Since we are interested in the sign of d, we can multiply by x = x 2 x 1 (that is a positive quantity) d i+1 x = { di x + 2(m 1) x = d i x + 2( y x) if d > 0 d i x + 2m x = d i x + 2 y if d 0 Eventually, we can impose d i = d i x (since both of them have the same sign) { 2( y x) if d > 0 d i+1 = d i + 2 y if d 0 Donato D Ambrosio (University of Calabria) Academic Year 2018/19 19 / 51
20 Rasterization Bresenham s line algorithm As regard the initial value, d can be set as follows: d = 2(y 2 y 1 ) (x 2 x 1 ) In this manner d > 0 when the angle is > 22.5 degs (and the North-East pixel is switched on) d 0 when the angle is 22.5 degs (and the East pixel si switched on) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 20 / 51
21 Bresenham s line algorithm Rasterization dx = x2 x1 ; dy = y2 y1 ; d = dy 2 dx ; incre = 2 dy ; incrne = 2 ( dy dx ) ; x = x1 ; y = y1 ; w r i t e P i x e l ( x, y, value ) ; while ( x < x2 ) { i f ( d <= 0) { d += incre ; x ++; } else { d += incrne ; x ++; y ++; } w r i t e P i x e l ( x, y, value ) ; } Donato D Ambrosio (University of Calabria) Academic Year 2018/19 21 / 51
22 Rasterization Scanline polygon algorithm The scanline algorithm is the reference algorithm for the scan conversion of polygons The algorithm uses scanlines to detect which pixels belong to the polygon Donato D Ambrosio (University of Calabria) Academic Year 2018/19 22 / 51
23 Rasterization Scanline polygon algorithm For each scanline, the intesections with the polygon s edges are evaluated and labeled with integer numbers (starting from 1) The pixels between odd-even couples (1-2, 3-4, ecc.) are switched on Note that the scanline y a intersects the edges 5 times: In such a case, the intersections 2 and 3 are considered as a single intersection since they are obtained on monotone edges At the contrary, the intersections 2 and 3 of the scanline y b are valid since the common vertex represent a local minimum (or maximum) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 23 / 51
24 Scanline polygon algorithm Rasterization The rasterization process starts from the bottom and from left to right Acoordingly, each next scanline differs by 1 along y The edge s slope is thus and therefore m = y i+1 y i x b x a = x b = x a + 1 m 1 x b x a Donato D Ambrosio (University of Calabria) Academic Year 2018/19 24 / 51
25 Rasterization Scanline polygon algorithm As a consequence, after the firt intesection (x a, y a ), the subsequent ones can be evaluated as (x b, y b ) = (x a + 1/m, y a + 1) The algorithm uses an edge table (ET), which is an array of pointers with as many entries as the framebuffer s scanlines Donato D Ambrosio (University of Calabria) Academic Year 2018/19 25 / 51
26 Rasterization Scanline polygon algorithm If non-null, the j th ET entry points to the list of edges that have minimum y equal to j The edges of each ET entry are ordered per minimum abscissa (x min ) in increasing order The inverse of the edge s slope (1/m) is also stored Donato D Ambrosio (University of Calabria) Academic Year 2018/19 26 / 51
27 Rasterization Scanline polygon algorithm An active edge table (AET) is also considered, which stores information about the edges intersected by the current scanline Differently from ET data, the second edge s information stores the current abscissa (of the scanline-edge intesection), inspite of the minimun one The figure below shows the AET content at two different stages of the algorithm, corresponding to the scanlines y = 11 and y = 18 Donato D Ambrosio (University of Calabria) Academic Year 2018/19 27 / 51
28 Rasterization Scanline polygon algorithm Once the ET has been defined, the algorithm processes the polygon as follows: 1 set the ordinate of the current scanline to the ordinate of the firt edge of the first entry of the ET (y = 5 in the example); 2 initialize AET to null (empty) 3 repeat the following steps until ET and AET are non empty: move the edges with ordinate y to the AET swhitch on the pixels between the odd-even intersections (1-2, 3-4, etc) remove the edges for which y = y max from AET (since they will not be interesected by the next scanline) increments y by 1 and x by 1/m (this latter only if the edge is not vertical) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 28 / 51
29 Hidden surface removal Hidden surface removal OpenGL rasterizes the primitives (e.g. triangles) in the order they appear into the vertex buffer object (VBO) In the case an object that is far from the observer is rasterized after another object that is nearer, the former can be erroneously overwriten (since it was first rasterized) An hidden surface removal algorithm can be used in this case (OpenGL adopts the z-buffer algorithm) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 29 / 51
30 Surface Culling Algorithms Hidden surface removal In order to minimize the amount of work required by the hidden surface removal algorithm, it is possible to remove one specific face of the primitives from the rasterization process (e.g. the back one, the face where the normal vector is applied or the face where the vertices are enumerated in clockwise order) If α denotes the angle between the normal vector and the observer direction, the cos α > 0 condition (i.e. 90 < α < 90 ) defines the primitive s front face The elimination of one or both primitive s faces can be enabled by means of the glcullface. The following example enables the cull face algorithm for the back faces glenable ( GL_CULL_FACE) ; glcullface (GL_BACK) ; Donato D Ambrosio (University of Calabria) Academic Year 2018/19 30 / 51
31 Hidden surface removal The z-buffer algorithm The z-buffer works together with the scan conversion and needs a further buffer called z-buffer to store depth information for each pixel The z-buffer is initialized to the distance between the observer and the far clipping plane During the scan conversion the distance of the pixel being rendered and the observer can be computed If this distance is lower than the distance stored into the z-buffer, then the pixel is visible and the z-buffer is updated with the pixel s depth Donato D Ambrosio (University of Calabria) Academic Year 2018/19 31 / 51
32 Hidden surface removal The z-buffer algorithm When the scan conversion of the polygon B is executed, its color will appear on the screen since its distance z 1 is less than the distance z 2 of the polygon A At the contrary, when the scan conversion of the polygon A the pixel corresponding to the intersection point will not appear on the screen Donato D Ambrosio (University of Calabria) Academic Year 2018/19 32 / 51
33 Light Table of contents 1 Algorithms Clipping Rasterization Hidden surface removal 2 Light The Phong Model Shading Donato D Ambrosio (University of Calabria) Academic Year 2018/19 33 / 51
34 Light Light Light Donato D Ambrosio (University of Calabria) Academic Year 2018/19 34 / 51
35 Light Light-Matter Interaction Light-Matter Interaction Lighting Model Is a mathematical formulation of the Light Equation It is fundamental for photo realistic rendering It defines how a point is lit as a function of: position into the three-dimensional space position of the (direct and indirect) sources position of the observer characteristics of the material The following terms are used in the context of the light equation: lighting, which refers to the amount of incident light radiation shading, which refers to the evaluation of the resulting color Donato D Ambrosio (University of Calabria) Academic Year 2018/19 35 / 51
36 Radiance Equation Light Light-Matter Interaction L o (ω, ω r ) = L e (ω, ω r ) + L r (x, Ω) From a position x and direction ω r, the amount of outgoing light L o is the sum of the emitted light L e and of the reflected light L r Donato D Ambrosio (University of Calabria) Academic Year 2018/19 36 / 51
37 Radiance Equation Light Light-Matter Interaction L r is the sum of the lights rays L i incoming from any direction ω i times cosθ by the surface s reflection formula f r L r = L i (x, ω i )( ω i n )f r (x, ω r, ω r )d ω i Ω Donato D Ambrosio (University of Calabria) Academic Year 2018/19 37 / 51
38 Light The Phong Model The Phong Model The radiance equation is impossible to be evaluated in real time with current hardware OpenGL, which is a real time API for 3D Computer Graphics, adopts the simplified Phong Model where: Only directional and point light sources are considered No inter-reflections are taken into account The light equation is evaluated locally, thus possible occluders are ignored f r is approximated with three constants (that are used to characterize the material of the reflecting surface) As a consequence, the only simulated phenomenon is the (specular and diffuse) reflection Donato D Ambrosio (University of Calabria) Academic Year 2018/19 38 / 51
39 Light The Phong Model The Phong Model: diffuse reflection The incoming rays are uniformly reflected in any direction The amount of light does not depend on the position of the observer and is proportional to the cosine of the angle between the incoming light and the surface normal (Lambert s law) Donato D Ambrosio (University of Calabria) Academic Year 2018/19 39 / 51
40 Light The Phong Model The Phong Model: diffuse reflection Phong s diffuse equation I diff = I p k d cosθ = I p k d ( N L ) Depends on: Surface orientation, N Light direction, L The surface s reflection function, which is approximated by the constant k d Donato D Ambrosio (University of Calabria) Academic Year 2018/19 40 / 51
41 Light The Phong Model The Phong Model: specular reflection The angle between the reflected light and the surface normal is equal to the angle between the incoming light and the normal (θ i = θ r ) As a consequence, the amount of light depends on the position of the observer Donato D Ambrosio (University of Calabria) Academic Year 2018/19 41 / 51
42 Light Phong s specular equation The Phong Model Specular Equation I spec = I p k s cos n α = I p k s ( R V ) n where k s is the constant used to approximate the surface s specular reflection function Donato D Ambrosio (University of Calabria) Academic Year 2018/19 42 / 51
43 Light The Phong Model The Phong Model: specular reflection The specular reflection is perceived as a spot highlight that depends on the position of the observer The highest highlight is obtained when α = 0 and decreases rapidly according to the law (cosα) n, where n [1, 128] is called specular reflection exponent Donato D Ambrosio (University of Calabria) Academic Year 2018/19 43 / 51
44 Phong ambient equation Light The Phong Model It is used to model the inter-reflections Phong s ambient equation I amb = I a k a where k a is a material dependent constant Donato D Ambrosio (University of Calabria) Academic Year 2018/19 44 / 51
45 Light The Phong Model Complete formulation of the Phong Model Complete formulation of the Phong Mode I = I a k a + p I p ( k d ( N L ) + k s ( R V ) n) The model can also account for the attenuation due to the distance by means of an attenuation factor Donato D Ambrosio (University of Calabria) Academic Year 2018/19 45 / 51
46 Light Shading Shading The color of a fragment is evaluated by applying a shading model The best shading model would consist in calculating the light equation for each pixel of the final image However, approximate solutions have to be adopted to obtain real time applications, especially on old hw Donato D Ambrosio (University of Calabria) Academic Year 2018/19 46 / 51
47 Light Shading Flat Shading The flat shading, is the simplest shading model consisting into evaluating the light equation once for the whole geometric primitive The same color is thus considered for each fragment of the primitive Donato D Ambrosio (University of Calabria) Academic Year 2018/19 47 / 51
48 Gouraud shading Light Shading Exploits the linearity of the RGB color space: the color of an inner fragment is obtained by linearly interpolating the colors of the vertices The light equation is thus evaluated for the vertices only Both the surface s normal (if known) or the average of the normal vectors evaluated for the vertex (since it is shared by more than one geometric primitive) can be considered Donato D Ambrosio (University of Calabria) Academic Year 2018/19 48 / 51
49 Gouraud shading Light Shading Donato D Ambrosio (University of Calabria) Academic Year 2018/19 49 / 51
50 Light Shading Phong shading It is the more sophisticated shading model and is the most used in the case of surfaces with a high specular reflection In spite of interpolating colors, the Phong shading interpolates the normals The lighting equation is evaluated for all the inner fragments of the geometric primitive by considering the interpolated normal vectors Donato D Ambrosio (University of Calabria) Academic Year 2018/19 50 / 51
51 Light Shading Comparison of different shading models Donato D Ambrosio (University of Calabria) Academic Year 2018/19 51 / 51
Lets assume each object has a defined colour. Hence our illumination model is looks unrealistic.
 Shading Models There are two main types of rendering that we cover, polygon rendering ray tracing Polygon rendering is used to apply illumination models to polygons, whereas ray tracing applies to arbitrary
Shading Models There are two main types of rendering that we cover, polygon rendering ray tracing Polygon rendering is used to apply illumination models to polygons, whereas ray tracing applies to arbitrary
Chapter 8: Implementation- Clipping and Rasterization
 Chapter 8: Implementation- Clipping and Rasterization Clipping Fundamentals Cohen-Sutherland Parametric Polygons Circles and Curves Text Basic Concepts: The purpose of clipping is to remove objects or
Chapter 8: Implementation- Clipping and Rasterization Clipping Fundamentals Cohen-Sutherland Parametric Polygons Circles and Curves Text Basic Concepts: The purpose of clipping is to remove objects or
CENG 477 Introduction to Computer Graphics. Ray Tracing: Shading
 CENG 477 Introduction to Computer Graphics Ray Tracing: Shading Last Week Until now we learned: How to create the primary rays from the given camera and image plane parameters How to intersect these rays
CENG 477 Introduction to Computer Graphics Ray Tracing: Shading Last Week Until now we learned: How to create the primary rays from the given camera and image plane parameters How to intersect these rays
Introduction Rasterization Z-buffering Shading. Graphics 2012/2013, 4th quarter. Lecture 09: graphics pipeline (rasterization and shading)
 Lecture 9 Graphics pipeline (rasterization and shading) Graphics pipeline - part 1 (recap) Perspective projection by matrix multiplication: x pixel y pixel z canonical 1 x = M vpm per M cam y z 1 This
Lecture 9 Graphics pipeline (rasterization and shading) Graphics pipeline - part 1 (recap) Perspective projection by matrix multiplication: x pixel y pixel z canonical 1 x = M vpm per M cam y z 1 This
FROM VERTICES TO FRAGMENTS. Lecture 5 Comp3080 Computer Graphics HKBU
 FROM VERTICES TO FRAGMENTS Lecture 5 Comp3080 Computer Graphics HKBU OBJECTIVES Introduce basic implementation strategies Clipping Scan conversion OCTOBER 9, 2011 2 OVERVIEW At end of the geometric pipeline,
FROM VERTICES TO FRAGMENTS Lecture 5 Comp3080 Computer Graphics HKBU OBJECTIVES Introduce basic implementation strategies Clipping Scan conversion OCTOBER 9, 2011 2 OVERVIEW At end of the geometric pipeline,
Topics. From vertices to fragments
 Topics From vertices to fragments From Vertices to Fragments Assign a color to every pixel Pass every object through the system Required tasks: Modeling Geometric processing Rasterization Fragment processing
Topics From vertices to fragments From Vertices to Fragments Assign a color to every pixel Pass every object through the system Required tasks: Modeling Geometric processing Rasterization Fragment processing
TSBK 07! Computer Graphics! Ingemar Ragnemalm, ISY
 1(84) Information Coding / Computer Graphics, ISY, LiTH TSBK 07 Computer Graphics Ingemar Ragnemalm, ISY 1(84) Lecture 5 3D graphics part 3 Illumination Illumination applied: Shading Surface detail: Mappings
1(84) Information Coding / Computer Graphics, ISY, LiTH TSBK 07 Computer Graphics Ingemar Ragnemalm, ISY 1(84) Lecture 5 3D graphics part 3 Illumination Illumination applied: Shading Surface detail: Mappings
Institutionen för systemteknik
 Code: Day: Lokal: M7002E 19 March E1026 Institutionen för systemteknik Examination in: M7002E, Computer Graphics and Virtual Environments Number of sections: 7 Max. score: 100 (normally 60 is required
Code: Day: Lokal: M7002E 19 March E1026 Institutionen för systemteknik Examination in: M7002E, Computer Graphics and Virtual Environments Number of sections: 7 Max. score: 100 (normally 60 is required
CS5620 Intro to Computer Graphics
 So Far wireframe hidden surfaces Next step 1 2 Light! Need to understand: How lighting works Types of lights Types of surfaces How shading works Shading algorithms What s Missing? Lighting vs. Shading
So Far wireframe hidden surfaces Next step 1 2 Light! Need to understand: How lighting works Types of lights Types of surfaces How shading works Shading algorithms What s Missing? Lighting vs. Shading
Pipeline Operations. CS 4620 Lecture Steve Marschner. Cornell CS4620 Spring 2018 Lecture 11
 Pipeline Operations CS 4620 Lecture 11 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives to pixels RASTERIZATION
Pipeline Operations CS 4620 Lecture 11 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives to pixels RASTERIZATION
Illumination and Shading
 Illumination and Shading Illumination (Lighting)! Model the interaction of light with surface points to determine their final color and brightness! The illumination can be computed either at vertices or
Illumination and Shading Illumination (Lighting)! Model the interaction of light with surface points to determine their final color and brightness! The illumination can be computed either at vertices or
CEng 477 Introduction to Computer Graphics Fall
 Illumination Models and Surface-Rendering Methods CEng 477 Introduction to Computer Graphics Fall 2007 2008 Illumination Models and Surface Rendering Methods In order to achieve realism in computer generated
Illumination Models and Surface-Rendering Methods CEng 477 Introduction to Computer Graphics Fall 2007 2008 Illumination Models and Surface Rendering Methods In order to achieve realism in computer generated
Shading. Shading = find color values at pixels of screen (when rendering a virtual 3D scene).
 Light Shading Shading Shading = find color values at pixels of screen (when rendering a virtual 3D scene). Shading Shading = find color values at pixels of screen (when rendering a virtual 3D scene). Same
Light Shading Shading Shading = find color values at pixels of screen (when rendering a virtual 3D scene). Shading Shading = find color values at pixels of screen (when rendering a virtual 3D scene). Same
CS452/552; EE465/505. Clipping & Scan Conversion
 CS452/552; EE465/505 Clipping & Scan Conversion 3-31 15 Outline! From Geometry to Pixels: Overview Clipping (continued) Scan conversion Read: Angel, Chapter 8, 8.1-8.9 Project#1 due: this week Lab4 due:
CS452/552; EE465/505 Clipping & Scan Conversion 3-31 15 Outline! From Geometry to Pixels: Overview Clipping (continued) Scan conversion Read: Angel, Chapter 8, 8.1-8.9 Project#1 due: this week Lab4 due:
Topic 9: Lighting & Reflection models 9/10/2016. Spot the differences. Terminology. Two Components of Illumination. Ambient Light Source
 Topic 9: Lighting & Reflection models Lighting & reflection The Phong reflection model diffuse component ambient component specular component Spot the differences Terminology Illumination The transport
Topic 9: Lighting & Reflection models Lighting & reflection The Phong reflection model diffuse component ambient component specular component Spot the differences Terminology Illumination The transport
Today s class. Simple shadows Shading Lighting in OpenGL. Informationsteknologi. Wednesday, November 21, 2007 Computer Graphics - Class 10 1
 Today s class Simple shadows Shading Lighting in OpenGL Wednesday, November 21, 27 Computer Graphics - Class 1 1 Simple shadows Simple shadows can be gotten by using projection matrices Consider a light
Today s class Simple shadows Shading Lighting in OpenGL Wednesday, November 21, 27 Computer Graphics - Class 1 1 Simple shadows Simple shadows can be gotten by using projection matrices Consider a light
From Vertices to Fragments: Rasterization. Reading Assignment: Chapter 7. Special memory where pixel colors are stored.
 From Vertices to Fragments: Rasterization Reading Assignment: Chapter 7 Frame Buffer Special memory where pixel colors are stored. System Bus CPU Main Memory Graphics Card -- Graphics Processing Unit (GPU)
From Vertices to Fragments: Rasterization Reading Assignment: Chapter 7 Frame Buffer Special memory where pixel colors are stored. System Bus CPU Main Memory Graphics Card -- Graphics Processing Unit (GPU)
Topic #1: Rasterization (Scan Conversion)
 Topic #1: Rasterization (Scan Conversion) We will generally model objects with geometric primitives points, lines, and polygons For display, we need to convert them to pixels for points it s obvious but
Topic #1: Rasterization (Scan Conversion) We will generally model objects with geometric primitives points, lines, and polygons For display, we need to convert them to pixels for points it s obvious but
Topic 9: Lighting & Reflection models. Lighting & reflection The Phong reflection model diffuse component ambient component specular component
 Topic 9: Lighting & Reflection models Lighting & reflection The Phong reflection model diffuse component ambient component specular component Spot the differences Terminology Illumination The transport
Topic 9: Lighting & Reflection models Lighting & reflection The Phong reflection model diffuse component ambient component specular component Spot the differences Terminology Illumination The transport
Surface shading: lights and rasterization. Computer Graphics CSE 167 Lecture 6
 Surface shading: lights and rasterization Computer Graphics CSE 167 Lecture 6 CSE 167: Computer Graphics Surface shading Materials Lights Rasterization 2 Scene data Rendering pipeline Modeling and viewing
Surface shading: lights and rasterization Computer Graphics CSE 167 Lecture 6 CSE 167: Computer Graphics Surface shading Materials Lights Rasterization 2 Scene data Rendering pipeline Modeling and viewing
Introduction to Visualization and Computer Graphics
 Introduction to Visualization and Computer Graphics DH2320, Fall 2015 Prof. Dr. Tino Weinkauf Introduction to Visualization and Computer Graphics Visibility Shading 3D Rendering Geometric Model Color Perspective
Introduction to Visualization and Computer Graphics DH2320, Fall 2015 Prof. Dr. Tino Weinkauf Introduction to Visualization and Computer Graphics Visibility Shading 3D Rendering Geometric Model Color Perspective
Computer Graphics. Illumination and Shading
 Rendering Pipeline modelling of geometry transformation into world coordinates placement of cameras and light sources transformation into camera coordinates backface culling projection clipping w.r.t.
Rendering Pipeline modelling of geometry transformation into world coordinates placement of cameras and light sources transformation into camera coordinates backface culling projection clipping w.r.t.
Pipeline Operations. CS 4620 Lecture 10
 Pipeline Operations CS 4620 Lecture 10 2008 Steve Marschner 1 Hidden surface elimination Goal is to figure out which color to make the pixels based on what s in front of what. Hidden surface elimination
Pipeline Operations CS 4620 Lecture 10 2008 Steve Marschner 1 Hidden surface elimination Goal is to figure out which color to make the pixels based on what s in front of what. Hidden surface elimination
Computer Graphics. Illumination and Shading
 () Illumination and Shading Dr. Ayman Eldeib Lighting So given a 3-D triangle and a 3-D viewpoint, we can set the right pixels But what color should those pixels be? If we re attempting to create a realistic
() Illumination and Shading Dr. Ayman Eldeib Lighting So given a 3-D triangle and a 3-D viewpoint, we can set the right pixels But what color should those pixels be? If we re attempting to create a realistic
CPSC / Illumination and Shading
 CPSC 599.64 / 601.64 Rendering Pipeline usually in one step modelling of geometry transformation into world coordinate system placement of cameras and light sources transformation into camera coordinate
CPSC 599.64 / 601.64 Rendering Pipeline usually in one step modelling of geometry transformation into world coordinate system placement of cameras and light sources transformation into camera coordinate
Pipeline Operations. CS 4620 Lecture 14
 Pipeline Operations CS 4620 Lecture 14 2014 Steve Marschner 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives
Pipeline Operations CS 4620 Lecture 14 2014 Steve Marschner 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives
Announcements. Midterms graded back at the end of class Help session on Assignment 3 for last ~20 minutes of class. Computer Graphics
 Announcements Midterms graded back at the end of class Help session on Assignment 3 for last ~20 minutes of class 1 Scan Conversion Overview of Rendering Scan Conversion Drawing Lines Drawing Polygons
Announcements Midterms graded back at the end of class Help session on Assignment 3 for last ~20 minutes of class 1 Scan Conversion Overview of Rendering Scan Conversion Drawing Lines Drawing Polygons
OpenGL Graphics System. 2D Graphics Primitives. Drawing 2D Graphics Primitives. 2D Graphics Primitives. Mathematical 2D Primitives.
 D Graphics Primitives Eye sees Displays - CRT/LCD Frame buffer - Addressable pixel array (D) Graphics processor s main function is to map application model (D) by projection on to D primitives: points,
D Graphics Primitives Eye sees Displays - CRT/LCD Frame buffer - Addressable pixel array (D) Graphics processor s main function is to map application model (D) by projection on to D primitives: points,
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Reality From Vertices to Fragments Overview Overall goal recapitulation: Input: World description, e.g., set of vertices and states for objects, attributes, camera,
Realtime 3D Computer Graphics Virtual Reality From Vertices to Fragments Overview Overall goal recapitulation: Input: World description, e.g., set of vertices and states for objects, attributes, camera,
Visualisatie BMT. Rendering. Arjan Kok
 Visualisatie BMT Rendering Arjan Kok a.j.f.kok@tue.nl 1 Lecture overview Color Rendering Illumination 2 Visualization pipeline Raw Data Data Enrichment/Enhancement Derived Data Visualization Mapping Abstract
Visualisatie BMT Rendering Arjan Kok a.j.f.kok@tue.nl 1 Lecture overview Color Rendering Illumination 2 Visualization pipeline Raw Data Data Enrichment/Enhancement Derived Data Visualization Mapping Abstract
Rasterizing triangles
 Rasterizing triangles We know how to project the vertices of a triangle in our model onto pixel centers. To draw the complete triangle, we have to decide which pixels to turn on. For now, let s assume
Rasterizing triangles We know how to project the vertices of a triangle in our model onto pixel centers. To draw the complete triangle, we have to decide which pixels to turn on. For now, let s assume
Deferred Rendering Due: Wednesday November 15 at 10pm
 CMSC 23700 Autumn 2017 Introduction to Computer Graphics Project 4 November 2, 2017 Deferred Rendering Due: Wednesday November 15 at 10pm 1 Summary This assignment uses the same application architecture
CMSC 23700 Autumn 2017 Introduction to Computer Graphics Project 4 November 2, 2017 Deferred Rendering Due: Wednesday November 15 at 10pm 1 Summary This assignment uses the same application architecture
COMP30019 Graphics and Interaction Scan Converting Polygons and Lines
 COMP30019 Graphics and Interaction Scan Converting Polygons and Lines Department of Computer Science and Software Engineering The Lecture outline Introduction Scan conversion Scan-line algorithm Edge coherence
COMP30019 Graphics and Interaction Scan Converting Polygons and Lines Department of Computer Science and Software Engineering The Lecture outline Introduction Scan conversion Scan-line algorithm Edge coherence
CS 130 Final. Fall 2015
 CS 130 Final Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
CS 130 Final Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
Illumination & Shading: Part 1
 Illumination & Shading: Part 1 Light Sources Empirical Illumination Shading Local vs Global Illumination Lecture 10 Comp 236 Spring 2005 Computer Graphics Jargon: Illumination Models Illumination - the
Illumination & Shading: Part 1 Light Sources Empirical Illumination Shading Local vs Global Illumination Lecture 10 Comp 236 Spring 2005 Computer Graphics Jargon: Illumination Models Illumination - the
Illumination Models & Shading
 Illumination Models & Shading Lighting vs. Shading Lighting Interaction between materials and light sources Physics Shading Determining the color of a pixel Computer Graphics ZBuffer(Scene) PutColor(x,y,Col(P));
Illumination Models & Shading Lighting vs. Shading Lighting Interaction between materials and light sources Physics Shading Determining the color of a pixel Computer Graphics ZBuffer(Scene) PutColor(x,y,Col(P));
Today. Global illumination. Shading. Interactive applications. Rendering pipeline. Computergrafik. Shading Introduction Local shading models
 Computergrafik Thomas Buchberger, Matthias Zwicker Universität Bern Herbst 2008 Today Introduction Local shading models Light sources strategies Compute interaction of light with surfaces Requires simulation
Computergrafik Thomas Buchberger, Matthias Zwicker Universität Bern Herbst 2008 Today Introduction Local shading models Light sources strategies Compute interaction of light with surfaces Requires simulation
Today. Global illumination. Shading. Interactive applications. Rendering pipeline. Computergrafik. Shading Introduction Local shading models
 Computergrafik Matthias Zwicker Universität Bern Herbst 2009 Today Introduction Local shading models Light sources strategies Compute interaction of light with surfaces Requires simulation of physics Global
Computergrafik Matthias Zwicker Universität Bern Herbst 2009 Today Introduction Local shading models Light sources strategies Compute interaction of light with surfaces Requires simulation of physics Global
Rasterization: Geometric Primitives
 Rasterization: Geometric Primitives Outline Rasterizing lines Rasterizing polygons 1 Rasterization: What is it? How to go from real numbers of geometric primitives vertices to integer coordinates of pixels
Rasterization: Geometric Primitives Outline Rasterizing lines Rasterizing polygons 1 Rasterization: What is it? How to go from real numbers of geometric primitives vertices to integer coordinates of pixels
Shading and Illumination
 Shading and Illumination OpenGL Shading Without Shading With Shading Physics Bidirectional Reflectance Distribution Function (BRDF) f r (ω i,ω ) = dl(ω ) L(ω i )cosθ i dω i = dl(ω ) L(ω i )( ω i n)dω
Shading and Illumination OpenGL Shading Without Shading With Shading Physics Bidirectional Reflectance Distribution Function (BRDF) f r (ω i,ω ) = dl(ω ) L(ω i )cosθ i dω i = dl(ω ) L(ω i )( ω i n)dω
RASTERISED RENDERING
 DH2323 DGI16 INTRODUCTION TO COMPUTER GRAPHICS AND INTERACTION RASTERISED RENDERING Christopher Peters HPCViz, KTH Royal Institute of Technology, Sweden chpeters@kth.se http://kth.academia.edu/christopheredwardpeters
DH2323 DGI16 INTRODUCTION TO COMPUTER GRAPHICS AND INTERACTION RASTERISED RENDERING Christopher Peters HPCViz, KTH Royal Institute of Technology, Sweden chpeters@kth.se http://kth.academia.edu/christopheredwardpeters
Illumination and Shading
 Illumination and Shading Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 2/14/07 1 From last time Texture mapping overview notation wrapping Perspective-correct interpolation Texture
Illumination and Shading Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 2/14/07 1 From last time Texture mapping overview notation wrapping Perspective-correct interpolation Texture
Lecture 15: Shading-I. CITS3003 Graphics & Animation
 Lecture 15: Shading-I CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Learn that with appropriate shading so objects appear as threedimensional
Lecture 15: Shading-I CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Learn that with appropriate shading so objects appear as threedimensional
CHAPTER 1 Graphics Systems and Models 3
 ?????? 1 CHAPTER 1 Graphics Systems and Models 3 1.1 Applications of Computer Graphics 4 1.1.1 Display of Information............. 4 1.1.2 Design.................... 5 1.1.3 Simulation and Animation...........
?????? 1 CHAPTER 1 Graphics Systems and Models 3 1.1 Applications of Computer Graphics 4 1.1.1 Display of Information............. 4 1.1.2 Design.................... 5 1.1.3 Simulation and Animation...........
Incremental Form. Idea. More efficient if we look at d k, the value of the decision variable at x = k
 Idea 1 m 0 candidates last pixel Note that line could have passed through any part of this pixel Decision variable: d = x(a-b) d is an integer d < 0 use upper pixel d > 0 use lower pixel Incremental Form
Idea 1 m 0 candidates last pixel Note that line could have passed through any part of this pixel Decision variable: d = x(a-b) d is an integer d < 0 use upper pixel d > 0 use lower pixel Incremental Form
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1
 graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1
 graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
Chapter 7 - Light, Materials, Appearance
 Chapter 7 - Light, Materials, Appearance Types of light in nature and in CG Shadows Using lights in CG Illumination models Textures and maps Procedural surface descriptions Literature: E. Angel/D. Shreiner,
Chapter 7 - Light, Materials, Appearance Types of light in nature and in CG Shadows Using lights in CG Illumination models Textures and maps Procedural surface descriptions Literature: E. Angel/D. Shreiner,
OXFORD ENGINEERING COLLEGE (NAAC Accredited with B Grade) DEPARTMENT OF COMPUTER SCIENCE & ENGINEERING LIST OF QUESTIONS
 OXFORD ENGINEERING COLLEGE (NAAC Accredited with B Grade) DEPARTMENT OF COMPUTER SCIENCE & ENGINEERING LIST OF QUESTIONS YEAR/SEM.: III/V STAFF NAME: T.ELANGOVAN SUBJECT NAME: Computer Graphics SUB. CODE:
OXFORD ENGINEERING COLLEGE (NAAC Accredited with B Grade) DEPARTMENT OF COMPUTER SCIENCE & ENGINEERING LIST OF QUESTIONS YEAR/SEM.: III/V STAFF NAME: T.ELANGOVAN SUBJECT NAME: Computer Graphics SUB. CODE:
OpenGl Pipeline. triangles, lines, points, images. Per-vertex ops. Primitive assembly. Texturing. Rasterization. Per-fragment ops.
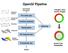 OpenGl Pipeline Individual Vertices Transformed Vertices Commands Processor Per-vertex ops Primitive assembly triangles, lines, points, images Primitives Fragments Rasterization Texturing Per-fragment
OpenGl Pipeline Individual Vertices Transformed Vertices Commands Processor Per-vertex ops Primitive assembly triangles, lines, points, images Primitives Fragments Rasterization Texturing Per-fragment
From Vertices To Fragments-1
 From Vertices To Fragments-1 1 Objectives Clipping Line-segment clipping polygon clipping 2 Overview At end of the geometric pipeline, vertices have been assembled into primitives Must clip out primitives
From Vertices To Fragments-1 1 Objectives Clipping Line-segment clipping polygon clipping 2 Overview At end of the geometric pipeline, vertices have been assembled into primitives Must clip out primitives
ECS 175 COMPUTER GRAPHICS. Ken Joy.! Winter 2014
 ECS 175 COMPUTER GRAPHICS Ken Joy Winter 2014 Shading To be able to model shading, we simplify Uniform Media no scattering of light Opaque Objects No Interreflection Point Light Sources RGB Color (eliminating
ECS 175 COMPUTER GRAPHICS Ken Joy Winter 2014 Shading To be able to model shading, we simplify Uniform Media no scattering of light Opaque Objects No Interreflection Point Light Sources RGB Color (eliminating
Rasterization, or What is glbegin(gl_lines) really doing?
 Rasterization, or What is glbegin(gl_lines) really doing? Course web page: http://goo.gl/eb3aa February 23, 2012 Lecture 4 Outline Rasterizing lines DDA/parametric algorithm Midpoint/Bresenham s algorithm
Rasterization, or What is glbegin(gl_lines) really doing? Course web page: http://goo.gl/eb3aa February 23, 2012 Lecture 4 Outline Rasterizing lines DDA/parametric algorithm Midpoint/Bresenham s algorithm
CPSC 314 LIGHTING AND SHADING
 CPSC 314 LIGHTING AND SHADING UGRAD.CS.UBC.CA/~CS314 slide credits: Mikhail Bessmeltsev et al 1 THE RENDERING PIPELINE Vertices and attributes Vertex Shader Modelview transform Per-vertex attributes Vertex
CPSC 314 LIGHTING AND SHADING UGRAD.CS.UBC.CA/~CS314 slide credits: Mikhail Bessmeltsev et al 1 THE RENDERING PIPELINE Vertices and attributes Vertex Shader Modelview transform Per-vertex attributes Vertex
CSE 167: Introduction to Computer Graphics Lecture #6: Lights. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016
 CSE 167: Introduction to Computer Graphics Lecture #6: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Thursday in class: midterm #1 Closed book Material
CSE 167: Introduction to Computer Graphics Lecture #6: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Thursday in class: midterm #1 Closed book Material
CEng 477 Introduction to Computer Graphics Fall 2007
 Visible Surface Detection CEng 477 Introduction to Computer Graphics Fall 2007 Visible Surface Detection Visible surface detection or hidden surface removal. Realistic scenes: closer objects occludes the
Visible Surface Detection CEng 477 Introduction to Computer Graphics Fall 2007 Visible Surface Detection Visible surface detection or hidden surface removal. Realistic scenes: closer objects occludes the
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into
 2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
Virtual Reality for Human Computer Interaction
 Virtual Reality for Human Computer Interaction Appearance: Lighting Representation of Light and Color Do we need to represent all I! to represent a color C(I)? No we can approximate using a three-color
Virtual Reality for Human Computer Interaction Appearance: Lighting Representation of Light and Color Do we need to represent all I! to represent a color C(I)? No we can approximate using a three-color
Mach band effect. The Mach band effect increases the visual unpleasant representation of curved surface using flat shading.
 Mach band effect The Mach band effect increases the visual unpleasant representation of curved surface using flat shading. A B 320322: Graphics and Visualization 456 Mach band effect The Mach band effect
Mach band effect The Mach band effect increases the visual unpleasant representation of curved surface using flat shading. A B 320322: Graphics and Visualization 456 Mach band effect The Mach band effect
From 3D World to 2D Screen. Hendrik Speleers
 Hendrik Speleers Overview Synthetic camera Rendering pipeline World window versus viewport Clipping Cohen-Sutherland algorithm Rasterizing Bresenham algorithm Three different actors in a scene Objects:
Hendrik Speleers Overview Synthetic camera Rendering pipeline World window versus viewport Clipping Cohen-Sutherland algorithm Rasterizing Bresenham algorithm Three different actors in a scene Objects:
The Traditional Graphics Pipeline
 Last Time? The Traditional Graphics Pipeline Participating Media Measuring BRDFs 3D Digitizing & Scattering BSSRDFs Monte Carlo Simulation Dipole Approximation Today Ray Casting / Tracing Advantages? Ray
Last Time? The Traditional Graphics Pipeline Participating Media Measuring BRDFs 3D Digitizing & Scattering BSSRDFs Monte Carlo Simulation Dipole Approximation Today Ray Casting / Tracing Advantages? Ray
The Traditional Graphics Pipeline
 Last Time? The Traditional Graphics Pipeline Reading for Today A Practical Model for Subsurface Light Transport, Jensen, Marschner, Levoy, & Hanrahan, SIGGRAPH 2001 Participating Media Measuring BRDFs
Last Time? The Traditional Graphics Pipeline Reading for Today A Practical Model for Subsurface Light Transport, Jensen, Marschner, Levoy, & Hanrahan, SIGGRAPH 2001 Participating Media Measuring BRDFs
Renderer Implementation: Basics and Clipping. Overview. Preliminaries. David Carr Virtual Environments, Fundamentals Spring 2005
 INSTITUTIONEN FÖR SYSTEMTEKNIK LULEÅ TEKNISKA UNIVERSITET Renderer Implementation: Basics and Clipping David Carr Virtual Environments, Fundamentals Spring 2005 Feb-28-05 SMM009, Basics and Clipping 1
INSTITUTIONEN FÖR SYSTEMTEKNIK LULEÅ TEKNISKA UNIVERSITET Renderer Implementation: Basics and Clipping David Carr Virtual Environments, Fundamentals Spring 2005 Feb-28-05 SMM009, Basics and Clipping 1
Raytracing CS148 AS3. Due :59pm PDT
 Raytracing CS148 AS3 Due 2010-07-25 11:59pm PDT We start our exploration of Rendering - the process of converting a high-level object-based description of scene into an image. We will do this by building
Raytracing CS148 AS3 Due 2010-07-25 11:59pm PDT We start our exploration of Rendering - the process of converting a high-level object-based description of scene into an image. We will do this by building
S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T
 S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T Copyright 2018 Sung-eui Yoon, KAIST freely available on the internet http://sglab.kaist.ac.kr/~sungeui/render
S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T Copyright 2018 Sung-eui Yoon, KAIST freely available on the internet http://sglab.kaist.ac.kr/~sungeui/render
Course Title: Computer Graphics Course no: CSC209
 Course Title: Computer Graphics Course no: CSC209 Nature of the Course: Theory + Lab Semester: III Full Marks: 60+20+20 Pass Marks: 24 +8+8 Credit Hrs: 3 Course Description: The course coversconcepts of
Course Title: Computer Graphics Course no: CSC209 Nature of the Course: Theory + Lab Semester: III Full Marks: 60+20+20 Pass Marks: 24 +8+8 Credit Hrs: 3 Course Description: The course coversconcepts of
Computer Graphics (CS 4731) Lecture 16: Lighting, Shading and Materials (Part 1)
 Computer Graphics (CS 4731) Lecture 16: Lighting, Shading and Materials (Part 1) Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) Why do we need Lighting & shading? Sphere
Computer Graphics (CS 4731) Lecture 16: Lighting, Shading and Materials (Part 1) Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) Why do we need Lighting & shading? Sphere
Ambient reflection. Jacobs University Visualization and Computer Graphics Lab : Graphics and Visualization 407
 Ambient reflection Phong reflection is a local illumination model. It only considers the reflection of light that directly comes from the light source. It does not compute secondary reflection of light
Ambient reflection Phong reflection is a local illumination model. It only considers the reflection of light that directly comes from the light source. It does not compute secondary reflection of light
Computer Graphics (CS 543) Lecture 7b: Intro to lighting, Shading and Materials + Phong Lighting Model
 Computer Graphics (CS 543) Lecture 7b: Intro to lighting, Shading and Materials + Phong Lighting Model Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) Why do we need Lighting
Computer Graphics (CS 543) Lecture 7b: Intro to lighting, Shading and Materials + Phong Lighting Model Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) Why do we need Lighting
Overview. Pipeline implementation I. Overview. Required Tasks. Preliminaries Clipping. Hidden Surface removal
 Overview Pipeline implementation I Preliminaries Clipping Line clipping Hidden Surface removal Overview At end of the geometric pipeline, vertices have been assembled into primitives Must clip out primitives
Overview Pipeline implementation I Preliminaries Clipping Line clipping Hidden Surface removal Overview At end of the geometric pipeline, vertices have been assembled into primitives Must clip out primitives
UNIT -8 IMPLEMENTATION
 UNIT -8 IMPLEMENTATION 1. Discuss the Bresenham s rasterization algorithm. How is it advantageous when compared to other existing methods? Describe. (Jun2012) 10M Ans: Consider drawing a line on a raster
UNIT -8 IMPLEMENTATION 1. Discuss the Bresenham s rasterization algorithm. How is it advantageous when compared to other existing methods? Describe. (Jun2012) 10M Ans: Consider drawing a line on a raster
Clipping and Scan Conversion
 15-462 Computer Graphics I Lecture 14 Clipping and Scan Conversion Line Clipping Polygon Clipping Clipping in Three Dimensions Scan Conversion (Rasterization) [Angel 7.3-7.6, 7.8-7.9] March 19, 2002 Frank
15-462 Computer Graphics I Lecture 14 Clipping and Scan Conversion Line Clipping Polygon Clipping Clipping in Three Dimensions Scan Conversion (Rasterization) [Angel 7.3-7.6, 7.8-7.9] March 19, 2002 Frank
CS 130 Exam I. Fall 2015
 CS 130 Exam I Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is
CS 130 Exam I Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is
Computer Vision Systems. Viewing Systems Projections Illuminations Rendering Culling and Clipping Implementations
 Computer Vision Systems Viewing Systems Projections Illuminations Rendering Culling and Clipping Implementations Viewing Systems Viewing Transformation Projective Transformation 2D Computer Graphics Devices
Computer Vision Systems Viewing Systems Projections Illuminations Rendering Culling and Clipping Implementations Viewing Systems Viewing Transformation Projective Transformation 2D Computer Graphics Devices
From Ver(ces to Fragments: Rasteriza(on
 From Ver(ces to Fragments: Rasteriza(on From Ver(ces to Fragments 3D vertices vertex shader rasterizer fragment shader final pixels 2D screen fragments l determine fragments to be covered l interpolate
From Ver(ces to Fragments: Rasteriza(on From Ver(ces to Fragments 3D vertices vertex shader rasterizer fragment shader final pixels 2D screen fragments l determine fragments to be covered l interpolate
INFOGR Computer Graphics. J. Bikker - April-July Lecture 10: Shading Models. Welcome!
 INFOGR Computer Graphics J. Bikker - April-July 2016 - Lecture 10: Shading Models Welcome! Today s Agenda: Introduction Light Transport Materials Sensors Shading INFOGR Lecture 10 Shading Models 3 Introduction
INFOGR Computer Graphics J. Bikker - April-July 2016 - Lecture 10: Shading Models Welcome! Today s Agenda: Introduction Light Transport Materials Sensors Shading INFOGR Lecture 10 Shading Models 3 Introduction
Module Contact: Dr Stephen Laycock, CMP Copyright of the University of East Anglia Version 1
 UNIVERSITY OF EAST ANGLIA School of Computing Sciences Main Series PG Examination 2013-14 COMPUTER GAMES DEVELOPMENT CMPSME27 Time allowed: 2 hours Answer any THREE questions. (40 marks each) Notes are
UNIVERSITY OF EAST ANGLIA School of Computing Sciences Main Series PG Examination 2013-14 COMPUTER GAMES DEVELOPMENT CMPSME27 Time allowed: 2 hours Answer any THREE questions. (40 marks each) Notes are
Last class. A vertex (w x, w y, w z, w) - clipping is in the - windowing and viewport normalized view volume if: - scan conversion/ rasterization
 Lecture 6 Last class Last lecture (clip coordinates): A vertex (w x, w y, w z, w) - clipping is in the - windowing and viewport normalized view volume if: - scan conversion/ rasterization normalized view
Lecture 6 Last class Last lecture (clip coordinates): A vertex (w x, w y, w z, w) - clipping is in the - windowing and viewport normalized view volume if: - scan conversion/ rasterization normalized view
Rendering Light Reflection Models
 Rendering Light Reflection Models Visual Imaging in the Electronic Age Donald P. Greenberg October 3, 2017 Lecture #13 Program of Computer Graphics, Cornell University General Electric - 167 Cornell in
Rendering Light Reflection Models Visual Imaging in the Electronic Age Donald P. Greenberg October 3, 2017 Lecture #13 Program of Computer Graphics, Cornell University General Electric - 167 Cornell in
Computing Visibility. Backface Culling for General Visibility. One More Trick with Planes. BSP Trees Ray Casting Depth Buffering Quiz
 Computing Visibility BSP Trees Ray Casting Depth Buffering Quiz Power of Plane Equations We ve gotten a lot of mileage out of one simple equation. Basis for D outcode-clipping Basis for plane-at-a-time
Computing Visibility BSP Trees Ray Casting Depth Buffering Quiz Power of Plane Equations We ve gotten a lot of mileage out of one simple equation. Basis for D outcode-clipping Basis for plane-at-a-time
CS 130 Exam I. Fall 2015
 S 3 Exam I Fall 25 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
S 3 Exam I Fall 25 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
Reflection and Shading
 Reflection and Shading R. J. Renka Department of Computer Science & Engineering University of North Texas 10/19/2015 Light Sources Realistic rendering requires that we model the interaction between light
Reflection and Shading R. J. Renka Department of Computer Science & Engineering University of North Texas 10/19/2015 Light Sources Realistic rendering requires that we model the interaction between light
CMSC427 Advanced shading getting global illumination by local methods. Credit: slides Prof. Zwicker
 CMSC427 Advanced shading getting global illumination by local methods Credit: slides Prof. Zwicker Topics Shadows Environment maps Reflection mapping Irradiance environment maps Ambient occlusion Reflection
CMSC427 Advanced shading getting global illumination by local methods Credit: slides Prof. Zwicker Topics Shadows Environment maps Reflection mapping Irradiance environment maps Ambient occlusion Reflection
Rasterization. COMP 575/770 Spring 2013
 Rasterization COMP 575/770 Spring 2013 The Rasterization Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives to
Rasterization COMP 575/770 Spring 2013 The Rasterization Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives to
CSE 167: Lecture #8: Lighting. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011
 CSE 167: Introduction to Computer Graphics Lecture #8: Lighting Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #4 due Friday, October 28 Introduction:
CSE 167: Introduction to Computer Graphics Lecture #8: Lighting Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #4 due Friday, October 28 Introduction:
3D Rasterization II COS 426
 3D Rasterization II COS 426 3D Rendering Pipeline (for direct illumination) 3D Primitives Modeling Transformation Lighting Viewing Transformation Projection Transformation Clipping Viewport Transformation
3D Rasterization II COS 426 3D Rendering Pipeline (for direct illumination) 3D Primitives Modeling Transformation Lighting Viewing Transformation Projection Transformation Clipping Viewport Transformation
The Traditional Graphics Pipeline
 Final Projects Proposals due Thursday 4/8 Proposed project summary At least 3 related papers (read & summarized) Description of series of test cases Timeline & initial task assignment The Traditional Graphics
Final Projects Proposals due Thursday 4/8 Proposed project summary At least 3 related papers (read & summarized) Description of series of test cases Timeline & initial task assignment The Traditional Graphics
SRM INSTITUTE OF SCIENCE AND TECHNOLOGY
 SRM INSTITUTE OF SCIENCE AND TECHNOLOGY DEPARTMENT OF INFORMATION TECHNOLOGY QUESTION BANK SUB.NAME: COMPUTER GRAPHICS SUB.CODE: IT307 CLASS : III/IT UNIT-1 2-marks 1. What is the various applications
SRM INSTITUTE OF SCIENCE AND TECHNOLOGY DEPARTMENT OF INFORMATION TECHNOLOGY QUESTION BANK SUB.NAME: COMPUTER GRAPHICS SUB.CODE: IT307 CLASS : III/IT UNIT-1 2-marks 1. What is the various applications
CS770/870 Spring 2017 Color and Shading
 Preview CS770/870 Spring 2017 Color and Shading Related material Cunningham: Ch 5 Hill and Kelley: Ch. 8 Angel 5e: 6.1-6.8 Angel 6e: 5.1-5.5 Making the scene more realistic Color models representing the
Preview CS770/870 Spring 2017 Color and Shading Related material Cunningham: Ch 5 Hill and Kelley: Ch. 8 Angel 5e: 6.1-6.8 Angel 6e: 5.1-5.5 Making the scene more realistic Color models representing the
Introduction to Computer Graphics. Farhana Bandukwala, PhD Lecture 14: Light Interacting with Surfaces
 Introduction to Computer Graphics Farhana Bandukwala, PhD Lecture 14: Light Interacting with Surfaces Outline Computational tools Reflection models Polygon shading Computation tools Surface normals Vector
Introduction to Computer Graphics Farhana Bandukwala, PhD Lecture 14: Light Interacting with Surfaces Outline Computational tools Reflection models Polygon shading Computation tools Surface normals Vector
CS 325 Computer Graphics
 CS 325 Computer Graphics 04 / 02 / 2012 Instructor: Michael Eckmann Today s Topics Questions? Comments? Illumination modelling Ambient, Diffuse, Specular Reflection Surface Rendering / Shading models Flat
CS 325 Computer Graphics 04 / 02 / 2012 Instructor: Michael Eckmann Today s Topics Questions? Comments? Illumination modelling Ambient, Diffuse, Specular Reflection Surface Rendering / Shading models Flat
Models and Architectures
 Models and Architectures Objectives Learn the basic design of a graphics system Introduce graphics pipeline architecture Examine software components for an interactive graphics system 1 Image Formation
Models and Architectures Objectives Learn the basic design of a graphics system Introduce graphics pipeline architecture Examine software components for an interactive graphics system 1 Image Formation
Problem Set 4 Part 1 CMSC 427 Distributed: Thursday, November 1, 2007 Due: Tuesday, November 20, 2007
 Problem Set 4 Part 1 CMSC 427 Distributed: Thursday, November 1, 2007 Due: Tuesday, November 20, 2007 Programming For this assignment you will write a simple ray tracer. It will be written in C++ without
Problem Set 4 Part 1 CMSC 427 Distributed: Thursday, November 1, 2007 Due: Tuesday, November 20, 2007 Programming For this assignment you will write a simple ray tracer. It will be written in C++ without
From Graphics to Visualization
 From Graphics to Visualization Introduction Light Sources Surface Lighting Effects Basic (Local ) Illumination Models Polgon-Rendering Methods Texture Mapping Transparenc and Blending Visualization Pipeline
From Graphics to Visualization Introduction Light Sources Surface Lighting Effects Basic (Local ) Illumination Models Polgon-Rendering Methods Texture Mapping Transparenc and Blending Visualization Pipeline
Lecture 17: Recursive Ray Tracing. Where is the way where light dwelleth? Job 38:19
 Lecture 17: Recursive Ray Tracing Where is the way where light dwelleth? Job 38:19 1. Raster Graphics Typical graphics terminals today are raster displays. A raster display renders a picture scan line
Lecture 17: Recursive Ray Tracing Where is the way where light dwelleth? Job 38:19 1. Raster Graphics Typical graphics terminals today are raster displays. A raster display renders a picture scan line
Line Drawing. Introduction to Computer Graphics Torsten Möller / Mike Phillips. Machiraju/Zhang/Möller
 Line Drawing Introduction to Computer Graphics Torsten Möller / Mike Phillips Rendering Pipeline Hardware Modelling Transform Visibility Illumination + Shading Perception, Color Interaction Texture/ Realism
Line Drawing Introduction to Computer Graphics Torsten Möller / Mike Phillips Rendering Pipeline Hardware Modelling Transform Visibility Illumination + Shading Perception, Color Interaction Texture/ Realism
Real-Time Graphics Architecture
 Real-Time Graphics Architecture Kurt Akeley Pat Hanrahan http://www.graphics.stanford.edu/courses/cs448a-01-fall Rasterization Outline Fundamentals Examples Special topics (Depth-buffer, cracks and holes,
Real-Time Graphics Architecture Kurt Akeley Pat Hanrahan http://www.graphics.stanford.edu/courses/cs448a-01-fall Rasterization Outline Fundamentals Examples Special topics (Depth-buffer, cracks and holes,
9. Illumination and Shading
 9. Illumination and Shading Approaches for visual realism: - Remove hidden surfaces - Shade visible surfaces and reproduce shadows - Reproduce surface properties Texture Degree of transparency Roughness,
9. Illumination and Shading Approaches for visual realism: - Remove hidden surfaces - Shade visible surfaces and reproduce shadows - Reproduce surface properties Texture Degree of transparency Roughness,
Interactive Real-Time Raycasting
 Interactive Real-Time Raycasting CS184 AS4 Due 2009-02-26 11:00pm We start our exploration of Rendering - the process of converting a high-level object-based description into a graphical image for display.
Interactive Real-Time Raycasting CS184 AS4 Due 2009-02-26 11:00pm We start our exploration of Rendering - the process of converting a high-level object-based description into a graphical image for display.
TDA362/DIT223 Computer Graphics EXAM (Same exam for both CTH- and GU students)
 TDA362/DIT223 Computer Graphics EXAM (Same exam for both CTH- and GU students) Saturday, January 13 th, 2018, 08:30-12:30 Examiner Ulf Assarsson, tel. 031-772 1775 Permitted Technical Aids None, except
TDA362/DIT223 Computer Graphics EXAM (Same exam for both CTH- and GU students) Saturday, January 13 th, 2018, 08:30-12:30 Examiner Ulf Assarsson, tel. 031-772 1775 Permitted Technical Aids None, except
