A THINNING ALGORITHM FOR TOPOLOGICALLY CORRECT 3D SURFACE RECONSTRUCTION
|
|
|
- Sheryl Gray
- 6 years ago
- Views:
Transcription
1 A THINNING ALGORITHM FOR TOPOLOGICALLY CORRECT 3D SURFACE RECONSTRUCTION Leonid Tcherniavski Department of Informatics University of Hamburg ABSTRACT The existing algorithms for 3D surface reconstruction from point clouds require objects with smooth surfaces and extremely dense samplings with no or only very few noise in order to guarantee a correct result. Moreover they can only be applied to single object reconstruction and not to segmentation of three or more regions. We have developed an alternative surface reconstruction method wich preserves the topological structure of multi-region objects under much weaker constraints. It is based on the Delaunay complex and α-shapes and uses a local thinning algorithm for the reconstruction of region boundaries. In this work we give a detailed analysis of its behaviour and we compare it with other approaches. KEY WORDS Surface Reconstruction, Topology Preservation, Alpha- Shapes, Delauney Trianguation. 1 Introduction A fundamental question of image analysis is how closely a computed image segmentation corresponds to the underlying real-world partition. Existing geometric sampling theorems are limited to binary partitions, where the space is split into (not necessarily connected) fore- and background components. In this case, the topology of the partition is preserved under various reconstruction schemes when the original regions are sufficiently smooth and the sampling is dense enough, e.g. see [4, 5]. Some approaches can also deal with noisy samplings, e.g. see [11, 12]. To our knowledge, all existing approaches for topologically correct surface reconstruction need an object to have a smooth surface, i.e. the surface curvature has to be everywhere bounded. This is often given by a bound on the so-called local feature size, which is the minimal distance of a surface point to the nearest point on the medial axis [4, 5, 11], but also by giving global smoothness constraints [12]. This is impossible for surfaces with edges (like e.g. a cube). Moreover they can deal only with binary partitions of the space, i.e. the problem of separating an object from its background by reconstructing the object boundary. Out aim is to be able to separate objects in more complicated configurations, i.e. to segment the 3D space into several regions, each being topologically correctly reconstructed. Peer Stelldinger Department of Informatics University of Hamburg stelldinger@informatik.uni-hamburg.de 2 Topologically Correct Reconstruction Since edges naturally occur when three or more regions meet, a reconstruction algorithm for multi-object segmentation tasks must be able to deal with non-smooth boundaries. Therefore we introduced the concept of r-stable partitions: A partition of the space R 3 into several regions r i is called r-stable when its boundary B = r i can be dilated by a closed ball of radius s without changing its homotopy type for any s r. Thus, regions in an r-stable partition do not change their topological information when one thickens the boundary moderately. Note, that r is also known as homological feature size [8]. Now, a sampling of the boundary is a set of (sampling) points which lie near the boundary B: A finite set of sampling points S = {s i R 3 } is called a (p, q)-sampling of the boundary B when the distance of every point b B to the nearest point in S is at most p, and the distance of every point s S to the nearest point in B is at most q. Thus, p denotes the sampling density, whereas q denotes the samplig accuracy. A sampling with q = 0 (i.e. all sampling points lie on the boundary) is called a strict sampling. Having a set of sampling points, we can construct the Delaunay complex and the α-complex. The α-complex D α (S) of a set of points S is defined as the subcomplex of the Delaunay complex of S which contains all cells C such that (1) the radius of the smallest sphere containing the sampling points of C is smaller than α, and it contains no other point of S, i.e. C 0 S =, or (2) an incident cell C with higher dimension is in D α (S). The polytope D α (S), i.e. the union of all elements of D α (S), is called α-shape. In case of sufficiently smooth surfaces and dense, noisefree samplings, the α-shape gives a good reconstruction of the original surface without changing topology [4, 5, 15]. But in other cases, the α-shape can not directly be used, it needs to be modified. Let D α (S) be the α-complex of a sampling S and D α (S) be its α-shape. Then the components of D α (S) c are called α-holes of D α (S). The (α, β)-holes of D α (S) are the α-holes H, where the largest radius of some n-cell in H is at least β α. The union of the α- shape D α with all α-holes of D α that are not (α, β)-holes
2 is called the (α, β)-shape reconstruction. Filling spurious holes in the α-shape reconstruction is a necessary step for getting a topologically correct boundary reconstruction. But there are also other problems regarding topology: although the (α, β)-shape reconstruction separates the different regions from each other, these regions may have small handles. In order to identify and remove these cases, we apply a homotopy type preserving thinning. We will denote an m-dimensional cell (m-cell) C in a cell complex D as simple if the number of cells of D which contain C is equal to one. Now the containing cell must be an (m + 1)-cell and the removal of the two cells (also called collapse, see [9] does neither change the homotopy type of the complex nor the topology of the background regions. Now the thinning algorithm for the (α, β)-shape reconstruction is as follows: Minimal (α, β)-shape reconstruction algorithm: 1. Given a (p, q)-sampling S of the boundary of some partition of the space, compute the α-complex of S with some α > p. 2. Add all cells to the complex, which belong to an α- hole which is no (α, β)-hole for β = α + p + q. 3. Find all simple m-cells (for any m with n > m 0) of the given (α, β)-shape reconstruction and put them in a priority queue by using the radii of the simple m- cells as priority, i.e. m-cells with big radius are the first to be removed. 4. As long as the queue is not empty: (a) Get the m-cell e with the highest priority from the queue. (b) If e is not simple anymore, it has lost this property during the removal of other cells. Skip the following and recommence with step 4. (c) Otherwise, remove e and the adjacent (m + 1)- cell t R from the boundary reconstruction. (d) Check whether the other cells adjacent to t have now become simple and put them in the queue if this is the case. 5. For m going from n 2 to 0 do: (a) Remove all m-cells of the complex, which do not have an adjacent (m+1)-cell in the complex. In [15] we proved that the minimal (α, β)-shape reconstruction algorithm is able to reconstruct the topological information of multi-object segmenations even in case of relatively coarse and noisy samplings: Theorem 1 Let P be an r-stable partition of the space R n, and S be a (p, q)-sampling of P s boundary B. Then the minimal (α, β)-shape reconstruction algorithm results in a cell complex D with D having the same homotopy type as B, and the components of B c are topologically equivalent to the components of D c, if (1) p < α r q, (2) β = α + p + q and (3) every region r i contains an open γ-disc with γ β + q > 2(p + q). 3 Comparison to other Approaches Surface reconstruction from sampling points has been of great interest in the last years. An overviev is given in table 1. One of the first approaches which gives a proof about the correct separation of an object from its background is the crust algorithm[4]. The drawback of this algorithm is, that it results in a triangle set, which only contains a correct triangulation of the surface instead of being one. This was corrected in the cocone algorithm. Both algorithms require relatively dense samplings in order to guaranty their correctness: while the crust algorithm requires a (p, 0)- sampling with p being at most equal to 0.1 times the local feature size (lfs), cocone needs p < 0.06lfs. In order to have a more intuitive measure we do not directly compare the necessary sampling density p, but the number N of sampling points one needs in order to reach such a density in case of a unit sphere (in this case, the local feature size is 1 and we have simply p 0.1). To compute this number is commonly known as the sphere covering problem and there exist very tight lower bounds for estimating this minimal number of sampling points( for a given ( 3 p, e.g. following ) ) [13] we get N 2 + 2π/ 6 arccot 2 (2 p2 ) π. In case of the crust and the cocone algorithm it follows that N 484, respectively N Both algorithms have been enhanced in several steps. E.g. power crust [6] is faster than crust and guarantees to reconstruct a correct surface in contrast to just containing one, and the modified power crust algorithm [11] can even deal with q 0.1. All three variants require p 0.1. Analogously tight cocone is a variant of cocone guaranteeing to reconstruct a watertight surface for the same bound as cocone, p < In contrast to these approaches much better bounds are given in [12]. Niyogi et al. use a global smoothness criterion instead of a local one, but are able to give much better bounds. In case of q = 0 only p < 0.48 is needed which is equivalent to only 22 well distributed sampling points, while p, q < (at least 165 sampling points) still allows to resonstruct a correct surface. In [15] an even better bound is given: by using the ball-pivoting algorithm the bounds given in [12] can be improved for q = 0 to p < r, which implies to use only 6 sampling points. As shown in the last section, a homeomorphic surface can also be reconstructed in case of highly noisy samplings, i.e. p + q < 1. Note, that in case of a sphere the restriction given by γ requires p + q < 0.5, but that in general the samplingdensity can locally be lower since the γ-bound must only be fulfilled somewhere in a region. All these methods require smooth surfaces. In [7] a method is given, which reconstructs Lipschitz Surfaces, and thus allows certain nonsmooth surfaces, but corners cannot have acute angles. The method works with locally adaptive but noise-free samplings and requires more than 263 points to result in a surface which is isotopic to a unit sphere boundary. To conclude, our approach gives better bounds on the necessary sampling density, on the accept-
3 able amount of noise and on the generality of the type of surfaces than previous approaches, and allowes for the first time to regard non-manifold partitions. sampling (p,q) # of points Crust [4] locally p adaptive q = 0 Co-Cone [5] locally p < adaptive q = 0 Power Crust [6] locally p Amenta et al. adaptive q = Tight Co-Cone [10] locally p < adaptive q = 0 [12] global p < q = 0 [12] global p < q < r Modified locally p 0.1r 484 Power Crust [11] adaptive q 0.1r Lipschitz locally p r 263 Surfaces [7] adaptive q 0 [15] global p < r 6 q = 0 [14] global p < 0.5r 78 q < r p Table 1. Comparison of different surface reconstruction algorithms. a) b) c) d) Figure 1. Surface of a unit sphere. The data set consists of 1001 nearly evenly distributed sample points with q = Implementation and Timings In the table below we show the breakup of the timings of the thinning reconstruction algorithm for a number of data sets on PC with 2000Mhz Intel Centrino Duo CPU and 2GB memory. The data sets [2, 1] were downsampled in order to show that our method does not require high resolution sampling for topologically correct surface reconstruction. The experiments were performed twice i.e. first with noise-free data, second with noise corrupted data. The corresponding p, q-values are to be found in the table. The corresponding results are demonstrated in Figures 5. As can be seen, the topology can even be reconstructed in cases when the geometry is heavily distorted by the noise. Please notice, that our implementation of the algorithm was designed for demonstration purposes. Thus, the timings are not to be considered to be optimal. data set points p q α-shape thinning millisec millisec Skeleton Hand Dragon Armadillo Angel Knots We divided the reconstruction procedure into two steps The α-shape builds the data structure by computing the Delaunay Triangulation and fills the data structure, α-shape computation, which stores for every element of the data structure the α-value and the Thinning procedure, which performes the topologically correct surface reconstruction. CGAL [3] library and its build in data structure was used for sampling represention, computation of the Delaunay triangulation and the α-shape. As it is descriped in the algorithm we have to delete simple cells from the reconstruction. For complexity reasons we used labels to classify the appropriate elements of the Delaunay Triangulation instead of changing the entire data structure. Thus, in the process of deletion we just remove the labels. We do not recommend to use the build-in function of sorting the triangulation elements in a list and use this list as a data structure. Though the usage of filter iterators is tempting for clean coding, the implementation of the required predicates is inefficient. We observed, that the thinning procedure required fourfould of the time given in the table above. Since the worst case complexity of computing α- shapes in 3D is O(n 2 ), and efficient priority queue implementations need O(log n) time both for push and pop, we get a worst case complexity of O(n 2 log n) for our algorithm. Nevertheless in case of typical surface sampling data we observe subquadratic time complexity.
4 Figure 2. Marked are some of irregularities of the α-shape: concavities (C), tunnels (T), bridges (B) 5 Experimental Evaluation First we are going to investigate which problems our algorithm has to solve due to the high amount of noise and also due to the fact that we allow non-smooth surfaces. To illustrate the subject matter we create a sampling data set corrupted by a great amount of noise. We sampled the surface of the unit sphere and added q = 0.45 error to the sample points. The original noise-free sampling is demonstrated as black triangulation in figure 1a, while the noisy triangulation is shown in blue. The result of surface reconstruction is shown in b. Geometrically it lies inside the dilation of radius q of the original surface (which is approximated in c), although the geometrical distortion is relatively high due to the linear dependence on the amount of noise. As shown in d, the α-shape contains cavities (spurious holes), which are filled by our algorithm. Figure 2 demostrates the alphashape of the surface. Some of the irregularities of the are marked i.e. α-shape concavities (C), tunnels (T), bridges (B). Figure 3 demonstrates the ability of our method to reconstruct the boundary of non-smooth and non-binary partitions with junctions and corners. We divided a cube into 8 equal regions by three intersecting squares. As it may be observed in Figure 3 the regions could be correctly reconstructed. 6 Figure 3. Reconstruction of a cube containing 8 regions Conclusions and Future Work Our method results in topologically equivalent components of the boundary. The given bounds are much better than previous ones, although in reality one often has to deal with even worse samplings. In fact in most of our experiments we had to estimate the values of p and q empirically, Figure 4. Surface Reconstruction in case of undersampled boundary but the algorithm behaved well even in cases where especially the bound given for γ was not fulfilled. Moreover for the first time it is possible to guaranty a topologically correct boundary reconstruction in case of non-smooth surfaces and in case of partitions into more than two regions. Nevertheless our approach is not robust to undersamplings, since the thinning algorithm strictly requires a sufficiently dense sampling of the whole surface. The result of such reconstruction may be seen in figure 4. The top left picture shows the undersampled part of the region which results in a hole in the surface. The thinned reconstruction is demonstrated in the top right picture. We see that the reconstruction containes only 7 regions du to the fact that the boundary of one region is completely removed by the thinning algorithm. In future we will try to overcome this problem. In addition to that we will try to adapt our method to adaptive sampling schemes. Acknowledgment The authors thank the Deutsche Forschungsgemeinschaft (DFG) for funding via project STI 147/2-1.
5 References [1] 3D Model Retrieval. dynamic/cgi-bin/databaseii v1.8/index.html. [2] Large Geometric Models Archive. gatech.edu/projects/large models/. [3] C GAL, Computational Geometry Algorithms Library. [4] N. Amenta, M. Bern, and M. Kamvysselis. A new voronoibased surface reconstruction algorithm. Conf. on Comp. Graph. and Interact. Techn., pages , [5] N. Amenta, S. Choi, T. Dey, and N. Leekha. A simple algorithm for homeomorphic surface reconstruction. Symp. on Comp. Geom., pages , [6] N. Amenta, S. Choi, and R. Kolluri. The power crust, unions of balls, and the medial axis transform. Comp. Geom., 19(2): , [7] J.-D. Boissonnat and S. Oudot. Provably good sampling and meshing of lipschitz surfaces. Proc. 22th Annual ACM Symposium on Computational Geometry, [8] D. Cohen-Steiner, H. Edelsbrunner, and J. Harer. Stability of persistence diagrams. Proc. 21th Annual ACM Symposium on Computational Geometry, pages , [9] T. Dey, H. Edelsbrunner, and S. Guha. Computational topology. Advances in Discrete and Computational Geometry, 223: , [10] T. Dey and S. Goswami. Tight cocone: A water-tight surface reconstructor. J. Comp. and Inf. Sci. in Engin., 3:302, [11] B. Mederos, N. Amenta, L. Velho, and L. de Figueiredo. Surface reconstruction from noisy point clouds. Eurographics Symp. on Geom. Proc., [12] P. Niyogi, S. Smale, and S. Weinberger. Finding the homology of submanifolds with high confidence from random samples. Discr. and Comp. Geom., 39(1), [13] P. Stelldinger. Tight bound for sphere covering and extension to r-regular sets. Submitted. [14] P. Stelldinger. Topologically correct 3d surface reconstruction and segmentation from noisy samples. Int. Worksh. Comb. Img. Anal., IWCIA, [15] P. Stelldinger. Topologically correct surface reconstruction using alpha shapes and relations to ball-pivoting. Submitted, 2008.
6 a) b) c) d) e) f) Figure 5. Noise-free and noise corrupted reconstruction
Estimating Geometry and Topology from Voronoi Diagrams
 Estimating Geometry and Topology from Voronoi Diagrams Tamal K. Dey The Ohio State University Tamal Dey OSU Chicago 07 p.1/44 Voronoi diagrams Tamal Dey OSU Chicago 07 p.2/44 Voronoi diagrams Tamal Dey
Estimating Geometry and Topology from Voronoi Diagrams Tamal K. Dey The Ohio State University Tamal Dey OSU Chicago 07 p.1/44 Voronoi diagrams Tamal Dey OSU Chicago 07 p.2/44 Voronoi diagrams Tamal Dey
Correctness. The Powercrust Algorithm for Surface Reconstruction. Correctness. Correctness. Delaunay Triangulation. Tools - Voronoi Diagram
 Correctness The Powercrust Algorithm for Surface Reconstruction Nina Amenta Sunghee Choi Ravi Kolluri University of Texas at Austin Boundary of a solid Close to original surface Homeomorphic to original
Correctness The Powercrust Algorithm for Surface Reconstruction Nina Amenta Sunghee Choi Ravi Kolluri University of Texas at Austin Boundary of a solid Close to original surface Homeomorphic to original
Computational Topology in Reconstruction, Mesh Generation, and Data Analysis
 Computational Topology in Reconstruction, Mesh Generation, and Data Analysis Tamal K. Dey Department of Computer Science and Engineering The Ohio State University Dey (2014) Computational Topology CCCG
Computational Topology in Reconstruction, Mesh Generation, and Data Analysis Tamal K. Dey Department of Computer Science and Engineering The Ohio State University Dey (2014) Computational Topology CCCG
The Medial Axis of the Union of Inner Voronoi Balls in the Plane
 The Medial Axis of the Union of Inner Voronoi Balls in the Plane Joachim Giesen a, Balint Miklos b,, Mark Pauly b a Max-Planck Institut für Informatik, Saarbrücken, Germany b Applied Geometry Group, ETH
The Medial Axis of the Union of Inner Voronoi Balls in the Plane Joachim Giesen a, Balint Miklos b,, Mark Pauly b a Max-Planck Institut für Informatik, Saarbrücken, Germany b Applied Geometry Group, ETH
Provably Good Moving Least Squares
 Provably Good Moving Least Squares Ravikrishna Kolluri Computer Science Division University of California at Berkeley 1 Problem Definition Given a set of samples on a closed surface build a representation
Provably Good Moving Least Squares Ravikrishna Kolluri Computer Science Division University of California at Berkeley 1 Problem Definition Given a set of samples on a closed surface build a representation
A Multicover Nerve for Geometric Inference. Don Sheehy INRIA Saclay, France
 A Multicover Nerve for Geometric Inference Don Sheehy INRIA Saclay, France Computational geometers use topology to certify geometric constructions. Computational geometers use topology to certify geometric
A Multicover Nerve for Geometric Inference Don Sheehy INRIA Saclay, France Computational geometers use topology to certify geometric constructions. Computational geometers use topology to certify geometric
A Constrained Delaunay Triangle Mesh Method for Three-Dimensional Unstructured Boundary Point Cloud
 International Journal of Computer Systems (ISSN: 2394-1065), Volume 03 Issue 02, February, 2016 Available at http://www.ijcsonline.com/ A Constrained Delaunay Triangle Mesh Method for Three-Dimensional
International Journal of Computer Systems (ISSN: 2394-1065), Volume 03 Issue 02, February, 2016 Available at http://www.ijcsonline.com/ A Constrained Delaunay Triangle Mesh Method for Three-Dimensional
Surface Reconstruction. Gianpaolo Palma
 Surface Reconstruction Gianpaolo Palma Surface reconstruction Input Point cloud With or without normals Examples: multi-view stereo, union of range scan vertices Range scans Each scan is a triangular mesh
Surface Reconstruction Gianpaolo Palma Surface reconstruction Input Point cloud With or without normals Examples: multi-view stereo, union of range scan vertices Range scans Each scan is a triangular mesh
66 III Complexes. R p (r) }.
 66 III Complexes III.4 Alpha Complexes In this section, we use a radius constraint to introduce a family of subcomplexes of the Delaunay complex. These complexes are similar to the Čech complexes but differ
66 III Complexes III.4 Alpha Complexes In this section, we use a radius constraint to introduce a family of subcomplexes of the Delaunay complex. These complexes are similar to the Čech complexes but differ
Surface reconstruction based on a dynamical system
 EUROGRAPHICS 2002 / G. Drettakis and H.-P. Seidel (Guest Editors) Volume 21 (2002), Number 3 Surface reconstruction based on a dynamical system N.N. Abstract We present an efficient algorithm that computes
EUROGRAPHICS 2002 / G. Drettakis and H.-P. Seidel (Guest Editors) Volume 21 (2002), Number 3 Surface reconstruction based on a dynamical system N.N. Abstract We present an efficient algorithm that computes
Simplicial Complexes: Second Lecture
 Simplicial Complexes: Second Lecture 4 Nov, 2010 1 Overview Today we have two main goals: Prove that every continuous map between triangulable spaces can be approximated by a simplicial map. To do this,
Simplicial Complexes: Second Lecture 4 Nov, 2010 1 Overview Today we have two main goals: Prove that every continuous map between triangulable spaces can be approximated by a simplicial map. To do this,
Simplicial Hyperbolic Surfaces
 Simplicial Hyperbolic Surfaces Talk by Ken Bromberg August 21, 2007 1-Lipschitz Surfaces- In this lecture we will discuss geometrically meaningful ways of mapping a surface S into a hyperbolic manifold
Simplicial Hyperbolic Surfaces Talk by Ken Bromberg August 21, 2007 1-Lipschitz Surfaces- In this lecture we will discuss geometrically meaningful ways of mapping a surface S into a hyperbolic manifold
Approximating Polygonal Objects by Deformable Smooth Surfaces
 Approximating Polygonal Objects by Deformable Smooth Surfaces Ho-lun Cheng and Tony Tan School of Computing, National University of Singapore hcheng,tantony@comp.nus.edu.sg Abstract. We propose a method
Approximating Polygonal Objects by Deformable Smooth Surfaces Ho-lun Cheng and Tony Tan School of Computing, National University of Singapore hcheng,tantony@comp.nus.edu.sg Abstract. We propose a method
ON THE WAY TO WATER-TIGHT MESH
 ON THE WAY TO WATER-TIGHT MESH Rui Liu, Darius Burschka, Gerd Hirzinger Institute of Robotics and Mechatronics, German Aerospace Center (DLR) Oberpfaffenhofen, 82234 Wessling, Germany. Rui.Liu@dlr.de KEY
ON THE WAY TO WATER-TIGHT MESH Rui Liu, Darius Burschka, Gerd Hirzinger Institute of Robotics and Mechatronics, German Aerospace Center (DLR) Oberpfaffenhofen, 82234 Wessling, Germany. Rui.Liu@dlr.de KEY
Outline of the presentation
 Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells
 VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells Scott A. Mitchell (speaker), joint work with Ahmed H. Mahmoud, Ahmad A. Rushdi, Scott A. Mitchell, Ahmad Abdelkader
VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells Scott A. Mitchell (speaker), joint work with Ahmed H. Mahmoud, Ahmad A. Rushdi, Scott A. Mitchell, Ahmad Abdelkader
Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D
 Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D Peer Stelldinger a Ullrich Köthe a a Cognitive Systems Group, University of Hamburg, Vogt-Köln-Str. 30, D-22527 Hamburg, Germany
Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D Peer Stelldinger a Ullrich Köthe a a Cognitive Systems Group, University of Hamburg, Vogt-Köln-Str. 30, D-22527 Hamburg, Germany
Spectral Surface Reconstruction from Noisy Point Clouds
 Spectral Surface Reconstruction from Noisy Point Clouds 1. Briefly summarize the paper s contributions. Does it address a new problem? Does it present a new approach? Does it show new types of results?
Spectral Surface Reconstruction from Noisy Point Clouds 1. Briefly summarize the paper s contributions. Does it address a new problem? Does it present a new approach? Does it show new types of results?
Skeleton Based Solid Representation with Topology Preservation
 Skeleton Based Solid Representation with Topology Preservation Ariel Shamir The Interdisciplinary Center Shaham Amir Tel-Aviv University Corresponding author: Dr. Ariel Shamir Efi Arazi School of Computer
Skeleton Based Solid Representation with Topology Preservation Ariel Shamir The Interdisciplinary Center Shaham Amir Tel-Aviv University Corresponding author: Dr. Ariel Shamir Efi Arazi School of Computer
The Ball-Pivoting Algorithm for Surface Reconstruction
 The Ball-Pivoting Algorithm for Surface Reconstruction 1. Briefly summarize the paper s contributions. Does it address a new problem? Does it present a new approach? Does it show new types of results?
The Ball-Pivoting Algorithm for Surface Reconstruction 1. Briefly summarize the paper s contributions. Does it address a new problem? Does it present a new approach? Does it show new types of results?
IJREAT International Journal of Research in Engineering & Advanced Technology, Volume 1, Issue 2, April-May, 2013 ISSN:
 Optimization of Mesh Reconstruction using Delaunay and Ball Pivoting Algorithm Bharti Sood 1, Kamaldeep Kaur 2 1, 2 Department of Electronics & Communication Engineering, BBSBEC, Fatehgarh Sahib, India
Optimization of Mesh Reconstruction using Delaunay and Ball Pivoting Algorithm Bharti Sood 1, Kamaldeep Kaur 2 1, 2 Department of Electronics & Communication Engineering, BBSBEC, Fatehgarh Sahib, India
Topologically Correct Image Segmentation Using Alpha Shapes
 Topologically Correct Image Segmentation Using Alpha Shapes Peer Stelldinger, Ullrich Köthe, and Hans Meine University of Hamburg, 22527 Hamburg, Germany Abstract. Existing theories on shape digitization
Topologically Correct Image Segmentation Using Alpha Shapes Peer Stelldinger, Ullrich Köthe, and Hans Meine University of Hamburg, 22527 Hamburg, Germany Abstract. Existing theories on shape digitization
Surface Reconstruction with MLS
 Surface Reconstruction with MLS Tobias Martin CS7960, Spring 2006, Feb 23 Literature An Adaptive MLS Surface for Reconstruction with Guarantees, T. K. Dey and J. Sun A Sampling Theorem for MLS Surfaces,
Surface Reconstruction with MLS Tobias Martin CS7960, Spring 2006, Feb 23 Literature An Adaptive MLS Surface for Reconstruction with Guarantees, T. K. Dey and J. Sun A Sampling Theorem for MLS Surfaces,
A Fast and Simple Surface Reconstruction Algorithm
 A Fast and Simple Surface Reconstruction Algorithm Siu-Wing Cheng Jiongxin Jin Man-Kit Lau Abstract We present an algorithm for surface reconstruction from a point cloud. It runs in O(n log n) time, where
A Fast and Simple Surface Reconstruction Algorithm Siu-Wing Cheng Jiongxin Jin Man-Kit Lau Abstract We present an algorithm for surface reconstruction from a point cloud. It runs in O(n log n) time, where
Lecture 5: Simplicial Complex
 Lecture 5: Simplicial Complex 2-Manifolds, Simplex and Simplicial Complex Scribed by: Lei Wang First part of this lecture finishes 2-Manifolds. Rest part of this lecture talks about simplicial complex.
Lecture 5: Simplicial Complex 2-Manifolds, Simplex and Simplicial Complex Scribed by: Lei Wang First part of this lecture finishes 2-Manifolds. Rest part of this lecture talks about simplicial complex.
Preferred directions for resolving the non-uniqueness of Delaunay triangulations
 Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
coding of various parts showing different features, the possibility of rotation or of hiding covering parts of the object's surface to gain an insight
 Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Isotopic Approximation within a Tolerance Volume
 Isotopic Approximation within a Tolerance Volume Manish Mandad David Cohen-Steiner Pierre Alliez Inria Sophia Antipolis - 1 Goals and Motivation - 2 Goals and Motivation Input: Tolerance volume of a surface
Isotopic Approximation within a Tolerance Volume Manish Mandad David Cohen-Steiner Pierre Alliez Inria Sophia Antipolis - 1 Goals and Motivation - 2 Goals and Motivation Input: Tolerance volume of a surface
Outline. Reconstruction of 3D Meshes from Point Clouds. Motivation. Problem Statement. Applications. Challenges
 Reconstruction of 3D Meshes from Point Clouds Ming Zhang Patrick Min cs598b, Geometric Modeling for Computer Graphics Feb. 17, 2000 Outline - problem statement - motivation - applications - challenges
Reconstruction of 3D Meshes from Point Clouds Ming Zhang Patrick Min cs598b, Geometric Modeling for Computer Graphics Feb. 17, 2000 Outline - problem statement - motivation - applications - challenges
Complex conforming Delaunay triangulation
 . RESEARCH PAPERS. SCIENCE CHINA Information Sciences June 2010 Vol. 53 No. 6: 1130 1140 doi: 10.1007/s11432-010-0097-6 Complex conforming Delaunay triangulation MENG XianHai 1, LI JiGang 1, YANG Qin 1,
. RESEARCH PAPERS. SCIENCE CHINA Information Sciences June 2010 Vol. 53 No. 6: 1130 1140 doi: 10.1007/s11432-010-0097-6 Complex conforming Delaunay triangulation MENG XianHai 1, LI JiGang 1, YANG Qin 1,
Computational Geometry
 Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Kurt Mehlhorn, MPI für Informatik. Curve and Surface Reconstruction p.1/25
 Curve and Surface Reconstruction Kurt Mehlhorn MPI für Informatik Curve and Surface Reconstruction p.1/25 Curve Reconstruction: An Example probably, you see more than a set of points Curve and Surface
Curve and Surface Reconstruction Kurt Mehlhorn MPI für Informatik Curve and Surface Reconstruction p.1/25 Curve Reconstruction: An Example probably, you see more than a set of points Curve and Surface
Three-Dimensional α Shapes
 Herbert Edelsbrunner and Ernst P. Mücke ACM Tran. Graph. 13(1), 1994 20 September 2005 1 2 α-complexes Edelsbrunner s Algorithm 3 Properties Surface Reconstruction Shape Question Given a set of points,
Herbert Edelsbrunner and Ernst P. Mücke ACM Tran. Graph. 13(1), 1994 20 September 2005 1 2 α-complexes Edelsbrunner s Algorithm 3 Properties Surface Reconstruction Shape Question Given a set of points,
Linear Complexity Hexahedral Mesh Generation
 Linear Complexity Hexahedral Mesh Generation David Eppstein Department of Information and Computer Science University of California, Irvine, CA 92717 http://www.ics.uci.edu/ eppstein/ Tech. Report 95-51
Linear Complexity Hexahedral Mesh Generation David Eppstein Department of Information and Computer Science University of California, Irvine, CA 92717 http://www.ics.uci.edu/ eppstein/ Tech. Report 95-51
Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image
 to appear in IEEE PAMI Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image Peer Stelldinger, Longin Jan Latecki and Marcelo Siqueira Abstract Digitization is not as
to appear in IEEE PAMI Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image Peer Stelldinger, Longin Jan Latecki and Marcelo Siqueira Abstract Digitization is not as
Surface Mesh Generation
 Surface Mesh Generation J.-F. Remacle Université catholique de Louvain September 22, 2011 0 3D Model For the description of the mesh generation process, let us consider the CAD model of a propeller presented
Surface Mesh Generation J.-F. Remacle Université catholique de Louvain September 22, 2011 0 3D Model For the description of the mesh generation process, let us consider the CAD model of a propeller presented
A fast algorithm for manifold reconstruction of surfaces
 Proceedings of the IMProVe 2011 International conference on Innovative Methods in Product Design June 15 th 17 th, 2011, Venice, Italy L. Di Angelo (a), L. Giaccari (a) (a) Department of Industrial Engineering,
Proceedings of the IMProVe 2011 International conference on Innovative Methods in Product Design June 15 th 17 th, 2011, Venice, Italy L. Di Angelo (a), L. Giaccari (a) (a) Department of Industrial Engineering,
Collars and Intestines: Practical Conforming Delaunay Refinement
 Collars and Intestines: Practical Conforming Delaunay Refinement Alexander Rand and Noel Walkington Carnegie Mellon University Summary. While several existing Delaunay refinement algorithms allow acute
Collars and Intestines: Practical Conforming Delaunay Refinement Alexander Rand and Noel Walkington Carnegie Mellon University Summary. While several existing Delaunay refinement algorithms allow acute
Shrinkwrap developments for computational electromagnetics in ICE NITe
 Shrinkwrap developments for computational electromagnetics in ICE NITe Preparing CAD models for electromagnetic analysis remains a complex, time consuming process. Typically, the CAD model will contain
Shrinkwrap developments for computational electromagnetics in ICE NITe Preparing CAD models for electromagnetic analysis remains a complex, time consuming process. Typically, the CAD model will contain
Critical Points of the Distance to an epsilon-sampling of a Surface and Flow-Complex-Based Surface Reconstruction
 Critical Points of the Distance to an epsilon-sampling of a Surface and Flow-Complex-Based Surface Reconstruction Tamal K. Dey Department of CSE Joachim Giesen Theoretische Informatik Edgar A. Ramos Dept.
Critical Points of the Distance to an epsilon-sampling of a Surface and Flow-Complex-Based Surface Reconstruction Tamal K. Dey Department of CSE Joachim Giesen Theoretische Informatik Edgar A. Ramos Dept.
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass
 Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Moving Least Squares Multiresolution Surface Approximation
 Moving Least Squares Multiresolution Surface Approximation BORIS MEDEROS LUIZ VELHO LUIZ HENRIQUE DE FIGUEIREDO IMPA Instituto de Matemática Pura e Aplicada Estrada Dona Castorina 110, 22461-320 Rio de
Moving Least Squares Multiresolution Surface Approximation BORIS MEDEROS LUIZ VELHO LUIZ HENRIQUE DE FIGUEIREDO IMPA Instituto de Matemática Pura e Aplicada Estrada Dona Castorina 110, 22461-320 Rio de
Final Project, Digital Geometry Processing
 Final Project, Digital Geometry Processing Shayan Hoshyari Student #: 81382153 December 2016 Introduction In this project an adaptive surface remesher has been developed based on the paper [1]. An algorithm
Final Project, Digital Geometry Processing Shayan Hoshyari Student #: 81382153 December 2016 Introduction In this project an adaptive surface remesher has been developed based on the paper [1]. An algorithm
An introduction to Topological Data Analysis through persistent homology: Intro and geometric inference
 Sophia-Antipolis, January 2016 Winter School An introduction to Topological Data Analysis through persistent homology: Intro and geometric inference Frédéric Chazal INRIA Saclay - Ile-de-France frederic.chazal@inria.fr
Sophia-Antipolis, January 2016 Winter School An introduction to Topological Data Analysis through persistent homology: Intro and geometric inference Frédéric Chazal INRIA Saclay - Ile-de-France frederic.chazal@inria.fr
Polygon decomposition. Motivation: Art gallery problem
 CG Lecture 3 Polygon decomposition 1. Polygon triangulation Triangulation theory Monotone polygon triangulation 2. Polygon decomposition into monotone pieces 3. Trapezoidal decomposition 4. Convex decomposition
CG Lecture 3 Polygon decomposition 1. Polygon triangulation Triangulation theory Monotone polygon triangulation 2. Polygon decomposition into monotone pieces 3. Trapezoidal decomposition 4. Convex decomposition
G 6i try. On the Number of Minimal 1-Steiner Trees* Discrete Comput Geom 12:29-34 (1994)
 Discrete Comput Geom 12:29-34 (1994) G 6i try 9 1994 Springer-Verlag New York Inc. On the Number of Minimal 1-Steiner Trees* B. Aronov, 1 M. Bern, 2 and D. Eppstein 3 Computer Science Department, Polytechnic
Discrete Comput Geom 12:29-34 (1994) G 6i try 9 1994 Springer-Verlag New York Inc. On the Number of Minimal 1-Steiner Trees* B. Aronov, 1 M. Bern, 2 and D. Eppstein 3 Computer Science Department, Polytechnic
topological data analysis and stochastic topology yuliy baryshnikov waikiki, march 2013
 topological data analysis and stochastic topology yuliy baryshnikov waikiki, march 2013 Promise of topological data analysis: extract the structure from the data. In: point clouds Out: hidden structure
topological data analysis and stochastic topology yuliy baryshnikov waikiki, march 2013 Promise of topological data analysis: extract the structure from the data. In: point clouds Out: hidden structure
A Developer s Survey of Polygonal Simplification algorithms. CS 563 Advanced Topics in Computer Graphics Fan Wu Mar. 31, 2005
 A Developer s Survey of Polygonal Simplification algorithms CS 563 Advanced Topics in Computer Graphics Fan Wu Mar. 31, 2005 Some questions to ask Why simplification? What are my models like? What matters
A Developer s Survey of Polygonal Simplification algorithms CS 563 Advanced Topics in Computer Graphics Fan Wu Mar. 31, 2005 Some questions to ask Why simplification? What are my models like? What matters
A fast and robust algorithm to count topologically persistent holes in noisy clouds
 A fast and robust algorithm to count topologically persistent holes in noisy clouds Vitaliy Kurlin Durham University Department of Mathematical Sciences, Durham, DH1 3LE, United Kingdom vitaliy.kurlin@gmail.com,
A fast and robust algorithm to count topologically persistent holes in noisy clouds Vitaliy Kurlin Durham University Department of Mathematical Sciences, Durham, DH1 3LE, United Kingdom vitaliy.kurlin@gmail.com,
Multi-View Matching & Mesh Generation. Qixing Huang Feb. 13 th 2017
 Multi-View Matching & Mesh Generation Qixing Huang Feb. 13 th 2017 Geometry Reconstruction Pipeline RANSAC --- facts Sampling Feature point detection [Gelfand et al. 05, Huang et al. 06] Correspondences
Multi-View Matching & Mesh Generation Qixing Huang Feb. 13 th 2017 Geometry Reconstruction Pipeline RANSAC --- facts Sampling Feature point detection [Gelfand et al. 05, Huang et al. 06] Correspondences
Möbius Transformations in Scientific Computing. David Eppstein
 Möbius Transformations in Scientific Computing David Eppstein Univ. of California, Irvine School of Information and Computer Science (including joint work with Marshall Bern from WADS 01 and SODA 03) Outline
Möbius Transformations in Scientific Computing David Eppstein Univ. of California, Irvine School of Information and Computer Science (including joint work with Marshall Bern from WADS 01 and SODA 03) Outline
The Topology of Skeletons and Offsets
 The Topology of Skeletons and Offsets Stefan Huber 1 1 B&R Industrial Automation stefan.huber@br-automation.com Abstract Given a polygonal shape with holes, we investigate the topology of two types of
The Topology of Skeletons and Offsets Stefan Huber 1 1 B&R Industrial Automation stefan.huber@br-automation.com Abstract Given a polygonal shape with holes, we investigate the topology of two types of
On the Locality of Extracting a 2-Manifold in IR 3
 On the Locality of Extracting a 2-Manifold in IR 3 Daniel Dumitriu 1, Stefan Funke 2, Martin Kutz, and Nikola Milosavljević 3 1 Max-Planck-Institut für Informatik Campus E 1.4, 66123 Saarbrücken, Germany
On the Locality of Extracting a 2-Manifold in IR 3 Daniel Dumitriu 1, Stefan Funke 2, Martin Kutz, and Nikola Milosavljević 3 1 Max-Planck-Institut für Informatik Campus E 1.4, 66123 Saarbrücken, Germany
Technical Report A Digital Topology-based Method for the Topological Filtering of a Reconstructed Surface
 Technical Report 2008-004 A Digital Topology-based Method for the Topological Filtering of a Reconstructed Surface D. Li a, M. Allili b a Université de Sherbrooke Department of Computer Science Sherbrooke,
Technical Report 2008-004 A Digital Topology-based Method for the Topological Filtering of a Reconstructed Surface D. Li a, M. Allili b a Université de Sherbrooke Department of Computer Science Sherbrooke,
Point-based Simplification Algorithm
 Point-based Simplification Algorithm Pai-Feng Lee 1, Bin-Shyan Jong 2 Department of Information Management, Hsing Wu College 1 Dept. of Information and Computer Engineering Engineering, Chung Yuan Christian
Point-based Simplification Algorithm Pai-Feng Lee 1, Bin-Shyan Jong 2 Department of Information Management, Hsing Wu College 1 Dept. of Information and Computer Engineering Engineering, Chung Yuan Christian
Smooth Surface Reconstruction from Noisy Clouds
 Smooth Surface Reconstruction from Noisy Clouds Boris Mederos, Luiz Velho and Luiz Henrique de Figueiredo IMPA Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina 110, 22461-320 Rio de Janeiro,
Smooth Surface Reconstruction from Noisy Clouds Boris Mederos, Luiz Velho and Luiz Henrique de Figueiredo IMPA Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina 110, 22461-320 Rio de Janeiro,
SURFACE RECONSTRUCTION FROM MULTI-VALUED GRID DATA
 4 th International Conference on Mechanical Engineering, December 26-28, 2001, Dhaka, Bangladesh/pp. VII 29-33 SURFACE RECONSTRUCTION FROM MULTI-VALUED GRID DATA S. Adithya and Dibakar Sen* Department
4 th International Conference on Mechanical Engineering, December 26-28, 2001, Dhaka, Bangladesh/pp. VII 29-33 SURFACE RECONSTRUCTION FROM MULTI-VALUED GRID DATA S. Adithya and Dibakar Sen* Department
Topological Issues in Hexahedral Meshing
 Topological Issues in Hexahedral Meshing David Eppstein Univ. of California, Irvine Dept. of Information and Computer Science Outline I. What is meshing? Problem statement Types of mesh Quality issues
Topological Issues in Hexahedral Meshing David Eppstein Univ. of California, Irvine Dept. of Information and Computer Science Outline I. What is meshing? Problem statement Types of mesh Quality issues
Topology Preserving Tetrahedral Decomposition of Trilinear Cell
 Topology Preserving Tetrahedral Decomposition of Trilinear Cell Bong-Soo Sohn Department of Computer Engineering, Kyungpook National University Daegu 702-701, South Korea bongbong@knu.ac.kr http://bh.knu.ac.kr/
Topology Preserving Tetrahedral Decomposition of Trilinear Cell Bong-Soo Sohn Department of Computer Engineering, Kyungpook National University Daegu 702-701, South Korea bongbong@knu.ac.kr http://bh.knu.ac.kr/
Clustering algorithms and introduction to persistent homology
 Foundations of Geometric Methods in Data Analysis 2017-18 Clustering algorithms and introduction to persistent homology Frédéric Chazal INRIA Saclay - Ile-de-France frederic.chazal@inria.fr Introduction
Foundations of Geometric Methods in Data Analysis 2017-18 Clustering algorithms and introduction to persistent homology Frédéric Chazal INRIA Saclay - Ile-de-France frederic.chazal@inria.fr Introduction
Stable and Multiscale Topological Signatures
 Stable and Multiscale Topological Signatures Mathieu Carrière, Steve Oudot, Maks Ovsjanikov Inria Saclay Geometrica April 21, 2015 1 / 31 Shape = point cloud in R d (d = 3) 2 / 31 Signature = mathematical
Stable and Multiscale Topological Signatures Mathieu Carrière, Steve Oudot, Maks Ovsjanikov Inria Saclay Geometrica April 21, 2015 1 / 31 Shape = point cloud in R d (d = 3) 2 / 31 Signature = mathematical
1 Proximity via Graph Spanners
 CS273: Algorithms for Structure Handout # 11 and Motion in Biology Stanford University Tuesday, 4 May 2003 Lecture #11: 4 May 2004 Topics: Proximity via Graph Spanners Geometric Models of Molecules, I
CS273: Algorithms for Structure Handout # 11 and Motion in Biology Stanford University Tuesday, 4 May 2003 Lecture #11: 4 May 2004 Topics: Proximity via Graph Spanners Geometric Models of Molecules, I
Surface Reconstruction
 Eurographics Symposium on Geometry Processing (2006) Surface Reconstruction 2009.12.29 Some methods for surface reconstruction Classification 1. Based on Delaunay triangulation(or Voronoi diagram) Alpha
Eurographics Symposium on Geometry Processing (2006) Surface Reconstruction 2009.12.29 Some methods for surface reconstruction Classification 1. Based on Delaunay triangulation(or Voronoi diagram) Alpha
Lecture 3: Art Gallery Problems and Polygon Triangulation
 EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
TERRAIN RECONSTRUCTION FROM GROUND BASED LASER DATA
 TERRAIN RECONSTRUCTION FROM GROUND BASED LASER DATA Bruce King1, Elzbieta Matuk1, Krzysztof Matuk1, Christopher M. Gold 1 Address: The Department of Land Surveying & Geo Informatics The Hong Kong Polytechnic
TERRAIN RECONSTRUCTION FROM GROUND BASED LASER DATA Bruce King1, Elzbieta Matuk1, Krzysztof Matuk1, Christopher M. Gold 1 Address: The Department of Land Surveying & Geo Informatics The Hong Kong Polytechnic
Topological estimation using witness complexes. Vin de Silva, Stanford University
 Topological estimation using witness complexes, Acknowledgements Gunnar Carlsson (Mathematics, Stanford) principal collaborator Afra Zomorodian (CS/Robotics, Stanford) persistent homology software Josh
Topological estimation using witness complexes, Acknowledgements Gunnar Carlsson (Mathematics, Stanford) principal collaborator Afra Zomorodian (CS/Robotics, Stanford) persistent homology software Josh
Voronoi diagram and Delaunay triangulation
 Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Geometric Modeling in Graphics
 Geometric Modeling in Graphics Part 10: Surface reconstruction Martin Samuelčík www.sccg.sk/~samuelcik samuelcik@sccg.sk Curve, surface reconstruction Finding compact connected orientable 2-manifold surface
Geometric Modeling in Graphics Part 10: Surface reconstruction Martin Samuelčík www.sccg.sk/~samuelcik samuelcik@sccg.sk Curve, surface reconstruction Finding compact connected orientable 2-manifold surface
Voronoi Diagram. Xiao-Ming Fu
 Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
The Cyclic Cycle Complex of a Surface
 The Cyclic Cycle Complex of a Surface Allen Hatcher A recent paper [BBM] by Bestvina, Bux, and Margalit contains a construction of a cell complex that gives a combinatorial model for the collection of
The Cyclic Cycle Complex of a Surface Allen Hatcher A recent paper [BBM] by Bestvina, Bux, and Margalit contains a construction of a cell complex that gives a combinatorial model for the collection of
Indexing by Shape of Image Databases Based on Extended Grid Files
 Indexing by Shape of Image Databases Based on Extended Grid Files Carlo Combi, Gian Luca Foresti, Massimo Franceschet, Angelo Montanari Department of Mathematics and ComputerScience, University of Udine
Indexing by Shape of Image Databases Based on Extended Grid Files Carlo Combi, Gian Luca Foresti, Massimo Franceschet, Angelo Montanari Department of Mathematics and ComputerScience, University of Udine
Homology and Persistent Homology Bootcamp Notes 2017
 Homology and Persistent Homology Bootcamp Notes Summer@ICERM 2017 Melissa McGuirl September 19, 2017 1 Preface This bootcamp is intended to be a review session for the material covered in Week 1 of Summer@ICERM
Homology and Persistent Homology Bootcamp Notes Summer@ICERM 2017 Melissa McGuirl September 19, 2017 1 Preface This bootcamp is intended to be a review session for the material covered in Week 1 of Summer@ICERM
Approximating Geodesic Distances on 2-Manifolds in R 3
 CCCG 2011, Toronto ON, August 10 12, 2011 Approximating Geodesic Distances on 2-Manifolds in R 3 Christian Scheffer Jan Vahrenhold Abstract We present an algorithm for approximating geodesic distances
CCCG 2011, Toronto ON, August 10 12, 2011 Approximating Geodesic Distances on 2-Manifolds in R 3 Christian Scheffer Jan Vahrenhold Abstract We present an algorithm for approximating geodesic distances
Complexity of Delaunay triangulation for points on lower-dimensional polyhedra
 Complexity of Delaunay triangulation for points on lower-dimensional polyhedra Nina Amenta UC Davis Dominique Attali CNRS-LIS Grenoble Olivier Devillers INRIA Sophia-Antipolis Abstract We show that the
Complexity of Delaunay triangulation for points on lower-dimensional polyhedra Nina Amenta UC Davis Dominique Attali CNRS-LIS Grenoble Olivier Devillers INRIA Sophia-Antipolis Abstract We show that the
A Simple Algorithm for Homeomorphic Surface Reconstruction
 A Simple Algorithm for Homeomorphic Surface Reconstruction N. Amenta* S. Choit T.K. Dey ~ N. Leekha Abstract 1 Introduction The problem of computing a piecewise linear approximation to a surface from a
A Simple Algorithm for Homeomorphic Surface Reconstruction N. Amenta* S. Choit T.K. Dey ~ N. Leekha Abstract 1 Introduction The problem of computing a piecewise linear approximation to a surface from a
Meshing Volumes with Curved Boundaries
 Engineering with Computers manuscript No. (will be inserted by the editor) Meshing Volumes with Curved Boundaries Steve Oudot 1, Laurent Rineau 2, Mariette Yvinec 3 1 INRIA, BP 93 06902 Sophia Antipolis,
Engineering with Computers manuscript No. (will be inserted by the editor) Meshing Volumes with Curved Boundaries Steve Oudot 1, Laurent Rineau 2, Mariette Yvinec 3 1 INRIA, BP 93 06902 Sophia Antipolis,
Topological Data Analysis - I. Afra Zomorodian Department of Computer Science Dartmouth College
 Topological Data Analysis - I Afra Zomorodian Department of Computer Science Dartmouth College September 3, 2007 1 Acquisition Vision: Images (2D) GIS: Terrains (3D) Graphics: Surfaces (3D) Medicine: MRI
Topological Data Analysis - I Afra Zomorodian Department of Computer Science Dartmouth College September 3, 2007 1 Acquisition Vision: Images (2D) GIS: Terrains (3D) Graphics: Surfaces (3D) Medicine: MRI
751 Problem Set I JWR. Due Sep 28, 2004
 751 Problem Set I JWR Due Sep 28, 2004 Exercise 1. For any space X define an equivalence relation by x y iff here is a path γ : I X with γ(0) = x and γ(1) = y. The equivalence classes are called the path
751 Problem Set I JWR Due Sep 28, 2004 Exercise 1. For any space X define an equivalence relation by x y iff here is a path γ : I X with γ(0) = x and γ(1) = y. The equivalence classes are called the path
Aspect-Ratio Voronoi Diagram with Applications
 Aspect-Ratio Voronoi Diagram with Applications Tetsuo Asano School of Information Science, JAIST (Japan Advanced Institute of Science and Technology), Japan 1-1 Asahidai, Nomi, Ishikawa, 923-1292, Japan
Aspect-Ratio Voronoi Diagram with Applications Tetsuo Asano School of Information Science, JAIST (Japan Advanced Institute of Science and Technology), Japan 1-1 Asahidai, Nomi, Ishikawa, 923-1292, Japan
Lecture 7: Jan 31, Some definitions related to Simplical Complex. 7.2 Topological Equivalence and Homeomorphism
 CS 6170 Computational Topology: Topological Data Analysis University of Utah Spring 2017 School of Computing Lecture 7: Jan 31, 2017 Lecturer: Prof. Bei Wang Scribe: Avani Sharma,
CS 6170 Computational Topology: Topological Data Analysis University of Utah Spring 2017 School of Computing Lecture 7: Jan 31, 2017 Lecturer: Prof. Bei Wang Scribe: Avani Sharma,
Geometric Inference. 1 Introduction. Frédéric Chazal 1 and David Cohen-Steiner 2
 Geometric Inference Frédéric Chazal 1 and David Cohen-Steiner 2 1 INRIA Futurs, 4 rue Jacques Monod - 91893 Orsay Cedex France frederic.chazal@inria.fr 2 INRIA Sophia-Antipolis, 2004 route des lucioles
Geometric Inference Frédéric Chazal 1 and David Cohen-Steiner 2 1 INRIA Futurs, 4 rue Jacques Monod - 91893 Orsay Cedex France frederic.chazal@inria.fr 2 INRIA Sophia-Antipolis, 2004 route des lucioles
Observing Information: Applied Computational Topology.
 Observing Information: Applied Computational Topology. Bangor University, and NUI Galway April 21, 2008 What is the geometric information that can be gleaned from a data cloud? Some ideas either already
Observing Information: Applied Computational Topology. Bangor University, and NUI Galway April 21, 2008 What is the geometric information that can be gleaned from a data cloud? Some ideas either already
Reconstructing Surfaces Using Envelopes: Bridging the Gap between Theory and Practice
 Reconstructing Surfaces Using Envelopes: Bridging the Gap between Theory and Practice Justin Bisceglio Blue Sky Studios, and University of Connecuticut, Department of Computer Science T.J. Peters University
Reconstructing Surfaces Using Envelopes: Bridging the Gap between Theory and Practice Justin Bisceglio Blue Sky Studios, and University of Connecuticut, Department of Computer Science T.J. Peters University
Pacific Journal of Mathematics
 Pacific Journal of Mathematics SIMPLIFYING TRIANGULATIONS OF S 3 Aleksandar Mijatović Volume 208 No. 2 February 2003 PACIFIC JOURNAL OF MATHEMATICS Vol. 208, No. 2, 2003 SIMPLIFYING TRIANGULATIONS OF S
Pacific Journal of Mathematics SIMPLIFYING TRIANGULATIONS OF S 3 Aleksandar Mijatović Volume 208 No. 2 February 2003 PACIFIC JOURNAL OF MATHEMATICS Vol. 208, No. 2, 2003 SIMPLIFYING TRIANGULATIONS OF S
Geometric Inference. 1 Introduction. Frédéric Chazal 1 and David Cohen-Steiner 2
 Geometric Inference Frédéric Chazal 1 and David Cohen-Steiner 2 1 INRIA Futurs, 4 rue Jacques Monod - 91893 Orsay Cedex France frederic.chazal@inria.fr 2 INRIA Sophia-Antipolis, 2004 route des lucioles
Geometric Inference Frédéric Chazal 1 and David Cohen-Steiner 2 1 INRIA Futurs, 4 rue Jacques Monod - 91893 Orsay Cedex France frederic.chazal@inria.fr 2 INRIA Sophia-Antipolis, 2004 route des lucioles
Tight Cocone DIEGO SALUME SEPTEMBER 18, 2013
 Tight Cocone DIEGO SALUME SEPTEMBER 18, 2013 Summary Problem: The Cocone algorithm produces surfaces with holes and artifacts in undersampled areas in the data. Solution: Extend the Cocone algorithm to
Tight Cocone DIEGO SALUME SEPTEMBER 18, 2013 Summary Problem: The Cocone algorithm produces surfaces with holes and artifacts in undersampled areas in the data. Solution: Extend the Cocone algorithm to
Complexity of Delaunay Triangulation for Points on Lower-dimensional Polyhedra.
 published in Proc. 18th ACM-SIAM Sympos. Discrete Algorithms (SODA) 2007, p.1106 1113. Complexity of Delaunay Triangulation for Points on Lower-dimensional Polyhedra. Nina Amenta UC Davis Dominique Attali
published in Proc. 18th ACM-SIAM Sympos. Discrete Algorithms (SODA) 2007, p.1106 1113. Complexity of Delaunay Triangulation for Points on Lower-dimensional Polyhedra. Nina Amenta UC Davis Dominique Attali
A CSP Search Algorithm with Reduced Branching Factor
 A CSP Search Algorithm with Reduced Branching Factor Igor Razgon and Amnon Meisels Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84-105, Israel {irazgon,am}@cs.bgu.ac.il
A CSP Search Algorithm with Reduced Branching Factor Igor Razgon and Amnon Meisels Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84-105, Israel {irazgon,am}@cs.bgu.ac.il
Fuzzy Voronoi Diagram
 Fuzzy Voronoi Diagram Mohammadreza Jooyandeh and Ali Mohades Khorasani Mathematics and Computer Science, Amirkabir University of Technology, Hafez Ave., Tehran, Iran mohammadreza@jooyandeh.info,mohades@aut.ac.ir
Fuzzy Voronoi Diagram Mohammadreza Jooyandeh and Ali Mohades Khorasani Mathematics and Computer Science, Amirkabir University of Technology, Hafez Ave., Tehran, Iran mohammadreza@jooyandeh.info,mohades@aut.ac.ir
Planar Graphs. 1 Graphs and maps. 1.1 Planarity and duality
 Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Processing 3D Surface Data
 Processing 3D Surface Data Computer Animation and Visualisation Lecture 17 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
Processing 3D Surface Data Computer Animation and Visualisation Lecture 17 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
Reflection groups 4. Mike Davis. May 19, Sao Paulo
 Reflection groups 4 Mike Davis Sao Paulo May 19, 2014 https://people.math.osu.edu/davis.12/slides.html 1 2 Exotic fundamental gps Nonsmoothable aspherical manifolds 3 Let (W, S) be a Coxeter system. S
Reflection groups 4 Mike Davis Sao Paulo May 19, 2014 https://people.math.osu.edu/davis.12/slides.html 1 2 Exotic fundamental gps Nonsmoothable aspherical manifolds 3 Let (W, S) be a Coxeter system. S
MARCHING CUBES AND VARIANTS
 CHAPTER MARCHING CUBES AND VARIANTS In the introduction, we mentioned four different approaches to isosurface construction. In this chapter, we describe one of those approaches to isosurface construction,
CHAPTER MARCHING CUBES AND VARIANTS In the introduction, we mentioned four different approaches to isosurface construction. In this chapter, we describe one of those approaches to isosurface construction,
Processing 3D Surface Data
 Processing 3D Surface Data Computer Animation and Visualisation Lecture 12 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
Processing 3D Surface Data Computer Animation and Visualisation Lecture 12 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
The Geodesic Integral on Medial Graphs
 The Geodesic Integral on Medial Graphs Kolya Malkin August 013 We define the geodesic integral defined on paths in the duals of medial graphs on surfaces and use it to study lens elimination and connection
The Geodesic Integral on Medial Graphs Kolya Malkin August 013 We define the geodesic integral defined on paths in the duals of medial graphs on surfaces and use it to study lens elimination and connection
Surface Reconstruction by Wrapping Finite Sets in Space
 Surface Reconstruction by Wrapping Finite Sets in Space Herbert Edelsbrunner Abstract Given a finite point set in, the surface reconstruction problem asks for a surface that passes through many but not
Surface Reconstruction by Wrapping Finite Sets in Space Herbert Edelsbrunner Abstract Given a finite point set in, the surface reconstruction problem asks for a surface that passes through many but not
35 CURVE AND SURFACE RECONSTRUCTION
 35 CURVE AND SURFACE RECONSTRUCTION Tamal K. Dey INTRODUCTION The problem of reconstructing a shape from its sample appears in many scientific and engineering applications. Because of the variety in shapes
35 CURVE AND SURFACE RECONSTRUCTION Tamal K. Dey INTRODUCTION The problem of reconstructing a shape from its sample appears in many scientific and engineering applications. Because of the variety in shapes
Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls
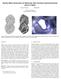 Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls Ho-Lun Cheng Xinwei Shi School of Computing National University of Singapore Figure 1: Molecular models of the molecule
Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls Ho-Lun Cheng Xinwei Shi School of Computing National University of Singapore Figure 1: Molecular models of the molecule
Mesh Generation. Jean-Daniel Boissonnat DataShape, INRIA
 Mesh Generation Jean-Daniel Boissonnat DataShape, INRIA http://www-sop.inria.fr/datashape Algorithmic Geometry Mesh generation J-D. Boissonnat 1 / 27 Meshing surfaces and 3D domains visualization and graphics
Mesh Generation Jean-Daniel Boissonnat DataShape, INRIA http://www-sop.inria.fr/datashape Algorithmic Geometry Mesh generation J-D. Boissonnat 1 / 27 Meshing surfaces and 3D domains visualization and graphics
Morphological Image Processing
 Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
