Mesh Generation. Jean-Daniel Boissonnat DataShape, INRIA
|
|
|
- Clara Austin
- 5 years ago
- Views:
Transcription
1 Mesh Generation Jean-Daniel Boissonnat DataShape, INRIA Algorithmic Geometry Mesh generation J-D. Boissonnat 1 / 27
2 Meshing surfaces and 3D domains visualization and graphics applications CAD and reverse engineering geometric modelling in medecine, geology, biology etc. autonomous exploration and mapping (SLAM) scientific computing : meshes for FEM dω o O P do Algorithmic Geometry Mesh generation J-D. Boissonnat 2 / 27
3 Mesh generation : from art to science Grid methods Lorensen & Cline [87] : marching cube Lopez & Brodlie [03] : topological consistency Plantiga & Vegter [04] : certified topology using interval arithmetic Morse theory Stander & Hart [97] B., Cohen-Steiner & Vegter [04] : certified topology Delaunay refinement Hermeline [84] Ruppert [95] Shewchuk [02] Chew [93] B. & Oudot [03,04] Cheng et al. [04] Algorithmic Geometry Mesh generation J-D. Boissonnat 3 / 27
4 Main issues Sampling How do we choose points in the domain? What information do we need to know/measure about the domain? Meshing How do we connect the points? Under what sampling conditions can we compute a good approximation of the domain? Algorithmic Geometry Mesh generation J-D. Boissonnat 4 / 27
5 Scale and dimension Algorithmic Geometry Mesh generation J-D. Boissonnat 5 / 27
6 Sampling conditions [Federer 1958], [Amenta & Bern 1998] Medial axis of M : axis(m) set of points with at least two closest points on M Local feature size and reach x M, lfs(x) = d(x, axis(m)) rch(m) = inf x M lfs(x) (ɛ, η)-net of M 1. P M, x M : d(x, P) ɛ lfs(x) 2. p, q P, p q ηε min(lfs(p), lfs(q)) Algorithmic Geometry Mesh generation J-D. Boissonnat 6 / 27
7 Sampling conditions [Federer 1958], [Amenta & Bern 1998] Medial axis of M : axis(m) set of points with at least two closest points on M Local feature size and reach x M, lfs(x) = d(x, axis(m)) rch(m) = inf x M lfs(x) (ɛ, η)-net of M 1. P M, x M : d(x, P) ɛ lfs(x) 2. p, q P, p q ηε min(lfs(p), lfs(q)) Algorithmic Geometry Mesh generation J-D. Boissonnat 6 / 27
8 Restricted Delaunay triangulation [Chew 93] Definition The restricted Delaunay triangulation Del X (P) to X R d is the nerve of Vor(P) X If P is an ε-sample, any ball centered on X that circumscribes a facet f of Del X(P) has a radius ε lfs(c f ) Algorithmic Geometry Mesh generation J-D. Boissonnat 7 / 27
9 Restricted Delaunay triangulation [Chew 93] Definition The restricted Delaunay triangulation Del X (P) to X R d is the nerve of Vor(P) X If P is an ε-sample, any ball centered on X that circumscribes a facet f of Del X(P) has a radius ε lfs(c f ) Algorithmic Geometry Mesh generation J-D. Boissonnat 7 / 27
10 Restricted Delaunay triangulation [Chew 93] Definition The restricted Delaunay triangulation Del X (P) to X R d is the nerve of Vor(P) X If P is an ε-sample, any ball centered on X that circumscribes a facet f of Del X(P) has a radius ε lfs(c f ) Algorithmic Geometry Mesh generation J-D. Boissonnat 7 / 27
11 Restricted Delaunay triangulation [Chew 93] Definition The restricted Delaunay triangulation Del X (P) to X R d is the nerve of Vor(P) X Algorithmic Geometry Mesh generation J-D. Boissonnat 8 / 27
12 Restricted Delaunay triang. of (ε, η)-nets [Amenta et al ], [B. & Oudot 2005] If then S R 3 is a compact surface of positive reach without boundary P is an (ε, η)-net with η cst and ε small enough Del S (S) provides good estimates of normals There exists a homeomorphism φ : Del S (P) S sup x ( φ(x) x ) = O(ε 2 ) Algorithmic Geometry Mesh generation J-D. Boissonnat 9 / 27
13 Surface mesh generationcontext byanddelaunay Motivation refinement Delaunay refinement meshing engine [Chew 1993, B. & Oudot 2003] φ : S R = Lipschitz The algorithms function refines: x S, 0 < Bad φ 0 = facets: η 0 ε rch(s) f Del S (P) φ(x) < ε lfs(x) oversized (sizing field) badly shaped (min angle bound) ORACLE : For a facet inaccurate f of Del (distance S (P), bound) return Bad c f, Tetrahedra r f and φ(c : f t) Del O (P) oversized (sizing field) A facet f is bad ifbadly-shaped r f > φ(c f ) (radius-egde ratio) Required oracle on domain to be meshed point location in domain and subdomains INIT compute intersection an initial detection/computation (small) sample Pbetween 0 S boundary surfaces and segments (Delaunay edges) REPEAT IF f is a bad facet insert in Del3D(c f ), update P and Del S (P) Algorithm PA-MY (INRIA Geometrica) CGALmesh ARC-ADT-AE / 3 UNTIL no bad facet remains Algorithmic Geometry Mesh generation J-D. Boissonnat 10 / 27
14 Surface mesh generationcontext byanddelaunay Motivation refinement Delaunay refinement meshing engine [Chew 1993, B. & Oudot 2003] φ : S R = Lipschitz The algorithms function refines: x S, 0 < Bad φ 0 = facets: η 0 ε rch(s) f Del S (P) φ(x) < ε lfs(x) oversized (sizing field) badly shaped (min angle bound) ORACLE : For a facet inaccurate f of Del (distance S (P), bound) return Bad c f, Tetrahedra r f and φ(c : f t) Del O (P) oversized (sizing field) A facet f is bad ifbadly-shaped r f > φ(c f ) (radius-egde ratio) Required oracle on domain to be meshed point location in domain and subdomains INIT compute intersection an initial detection/computation (small) sample Pbetween 0 S boundary surfaces and segments (Delaunay edges) REPEAT IF f is a bad facet insert in Del3D(c f ), update P and Del S (P) Algorithm PA-MY (INRIA Geometrica) CGALmesh ARC-ADT-AE / 3 UNTIL no bad facet remains Algorithmic Geometry Mesh generation J-D. Boissonnat 10 / 27
15 The meshing algorithm in action Algorithmic Geometry Mesh generation J-D. Boissonnat 11 / 27
16 The algorithm outputs a loose net of S Separation p P, d(p, P \ {p}) = p q min(φ(p), φ(q)) φ(p) p q (φ is Lipschitz) p q 1 2 φ(p) 1 2 φ 0 > 0 the algorithm terminates Density Each facet has a S-radius rf φ(c f ) < ε lfs(c f ) If correctly initialized, Del S (P) has a vertex on each cc of S Algorithmic Geometry Mesh generation J-D. Boissonnat 12 / 27
17 Size of the sample = Θ ( S ) dx φ 2 (x) Upper bound B p = B(p, φ(p) ), p P 2 dx S φ 2 (x) p 4 9 (B p S) dx φ 2 (x) area(b p S) p φ 2 (p) p C = C P (the B p are disjoint) φ(x) φ(p) + p x 3 2 φ(p)) reach(s) p Lower bound Use a covering instead of a packing φ(p) 2 Algorithmic Geometry Mesh generation J-D. Boissonnat 13 / 27
18 Size of the sample = Θ ( S ) dx φ 2 (x) Upper bound B p = B(p, φ(p) ), p P 2 dx S φ 2 (x) p 4 9 (B p S) dx φ 2 (x) area(b p S) p φ 2 (p) p C = C P (the B p are disjoint) φ(x) φ(p) + p x 3 2 φ(p)) reach(s) p Lower bound Use a covering instead of a packing φ(p) 2 Algorithmic Geometry Mesh generation J-D. Boissonnat 13 / 27
19 Chord lemma Let x and y be two points of M. We have 1 sin (xy, T x ) x y 2 rch(m) ; 2 the distance from y to T x is at most x y 2 2 rch(m). 2θ x y x y = 2 rch(m) sin (xy, T x ) D q y y = x y sin (xy, T x ) M θ q x y 2 2 rch(m) T p p q Algorithmic Geometry Mesh generation J-D. Boissonnat 14 / 27
20 Tangent space approximation Lemma [Whitney 1957] If σ is a j-simplex whose vertices all lie within a distance h from a hyperplane H R d, then Corollary sin (aff (σ), H) 2j h D(σ) = 2h Θ(σ) (σ) If σ is a j-simplex, j k, vert (σ) M, (σ) 2ε rch(m) (h (σ)2 by the Chord Lemma) 2 rch(m) p σ, sin (aff(σ), T p ) 2ε Θ(σ) Algorithmic Geometry Mesh generation J-D. Boissonnat 15 / 27
21 Schwarz lantern Algorithmic Geometry Mesh generation J-D. Boissonnat 16 / 27
22 Thickness and angle bounds for triangles Thickness and angle bounds for triangles c b R h a h = ab sin sinb b = ab ab ac ac Θ(abc) (abc) = = h h 2R 2 h 2 4R = 2 2 h 4R φ2 0 32R 8 φ ε rch(s) 8 sin b 2 φ = 0 2ε rch(s) 2 Algorithmic Geometry Mesh generation J-D. Boissonnat 17 / 28 Algorithmic Geometry Mesh generation J-D. Boissonnat 17 / 27
23 Triangulated pseudo-surface For ε small enough, Del S (P) is a triangulated pseudo-surface v v Any edge e of Del S (P) has exactly two incident facets The adjacency graph of the facets is connected Algorithmic Geometry Mesh generation J-D. Boissonnat 18 / 27
24 Triangulated pseudo-surface e an edge of ˆM, f any face incident on e 1 V(p) bounded V(e) S is even 2 V(f ) intersects S at most once O V (e) V(e) Proof of 2 by contradiction: c, c V(f ) S a. c c 2ε rch(s) sin (cc, T c ) ε (Chord L.) b. cc f (dual face) c. T c aff (f ) (Whitney s L.) Algorithmic Geometry Mesh generation J-D. Boissonnat 19 / 27
25 Triangulated pseudo-surface e an edge of ˆM, f any face incident on e 1 V(p) bounded V(e) S is even 2 V(f ) intersects S at most once O V (e) V(e) Proof of 2 by contradiction: c, c V(f ) S a. c c 2ε rch(s) sin (cc, T c ) ε (Chord L.) b. cc f (dual face) c. T c aff (f ) (Whitney s L.) Algorithmic Geometry Mesh generation J-D. Boissonnat 19 / 27
26 The main result The Delaunay refinement algorithm produces an ε- net P of S a triangulated surface Ŝ homeomorphic to S close to S (Hausdorff/Fréchet distance O(ε 2 ), approximation of normals O(ε)) Algorithmic Geometry Mesh generation J-D. Boissonnat 20 / 27
27 Applications Implicit surfaces f (x, y, z) = 0 Isosurfaces in a 3d image (Medical images) Triangulated surfaces (Remeshing) Point sets (Surface reconstruction) see cgal.org, CGALmesh project Algorithmic Geometry Mesh generation J-D. Boissonnat 21 / 27
28 Results on smooth implicit surfaces Algorithmic Geometry Mesh generation J-D. Boissonnat 22 / 27
29 CGALmesh Achievements Meshing 3D domains Input from segmented 3D medical images [INSERM] PA-MY (INRIA Geometrica) Algorithmic Geometry [SIEMENS] CGALmesh Mesh generation ARC-ADT-AE-2010 J-D. Boissonnat 22 / / 27
30 Comparison with the Marching Cube algorithm Marching cube Delaunay refinement Algorithmic Geometry Mesh generation J-D. Boissonnat 24 / 27
31 CGALmesh Achievements Meshing with sharp features Apolyhedralexample PA-MY (INRIA Geometrica) CGALmesh ARC-ADT-AE / 36 Algorithmic Geometry Mesh generation J-D. Boissonnat 25 / 27
32 CGALmesh Achievements Meshing 3D multi-domains Input from segmented 3D medical images [IRCAD] PA-MY (INRIA Geometrica) CGALmesh ARC-ADT-AE / 36 Algorithmic Geometry Mesh generation J-D. Boissonnat 26 / 27
33 Surface reconstruction from unorganized point sets Courtesy of P. Alliez Algorithmic Geometry Mesh generation J-D. Boissonnat 27 / 27
Estimating Geometry and Topology from Voronoi Diagrams
 Estimating Geometry and Topology from Voronoi Diagrams Tamal K. Dey The Ohio State University Tamal Dey OSU Chicago 07 p.1/44 Voronoi diagrams Tamal Dey OSU Chicago 07 p.2/44 Voronoi diagrams Tamal Dey
Estimating Geometry and Topology from Voronoi Diagrams Tamal K. Dey The Ohio State University Tamal Dey OSU Chicago 07 p.1/44 Voronoi diagrams Tamal Dey OSU Chicago 07 p.2/44 Voronoi diagrams Tamal Dey
Meshing Volumes with Curved Boundaries
 Engineering with Computers manuscript No. (will be inserted by the editor) Meshing Volumes with Curved Boundaries Steve Oudot 1, Laurent Rineau 2, Mariette Yvinec 3 1 INRIA, BP 93 06902 Sophia Antipolis,
Engineering with Computers manuscript No. (will be inserted by the editor) Meshing Volumes with Curved Boundaries Steve Oudot 1, Laurent Rineau 2, Mariette Yvinec 3 1 INRIA, BP 93 06902 Sophia Antipolis,
Voronoi Diagrams, Delaunay Triangulations and Polytopes
 Voronoi Diagrams, Delaunay Triangulations and Polytopes Jean-Daniel Boissonnat MPRI, Lecture 2 Computational Geometry Learning Voronoi, Delaunay & Polytopes MPRI, Lecture 2 1 / 43 Voronoi diagrams in nature
Voronoi Diagrams, Delaunay Triangulations and Polytopes Jean-Daniel Boissonnat MPRI, Lecture 2 Computational Geometry Learning Voronoi, Delaunay & Polytopes MPRI, Lecture 2 1 / 43 Voronoi diagrams in nature
Computational Topology in Reconstruction, Mesh Generation, and Data Analysis
 Computational Topology in Reconstruction, Mesh Generation, and Data Analysis Tamal K. Dey Department of Computer Science and Engineering The Ohio State University Dey (2014) Computational Topology CCCG
Computational Topology in Reconstruction, Mesh Generation, and Data Analysis Tamal K. Dey Department of Computer Science and Engineering The Ohio State University Dey (2014) Computational Topology CCCG
Collars and Intestines: Practical Conforming Delaunay Refinement
 Collars and Intestines: Practical Conforming Delaunay Refinement Alexander Rand and Noel Walkington Carnegie Mellon University Summary. While several existing Delaunay refinement algorithms allow acute
Collars and Intestines: Practical Conforming Delaunay Refinement Alexander Rand and Noel Walkington Carnegie Mellon University Summary. While several existing Delaunay refinement algorithms allow acute
Provably Good Moving Least Squares
 Provably Good Moving Least Squares Ravikrishna Kolluri Computer Science Division University of California at Berkeley 1 Problem Definition Given a set of samples on a closed surface build a representation
Provably Good Moving Least Squares Ravikrishna Kolluri Computer Science Division University of California at Berkeley 1 Problem Definition Given a set of samples on a closed surface build a representation
Lecture 1 Discrete Geometric Structures
 Lecture 1 Discrete Geometric Structures Jean-Daniel Boissonnat Winter School on Computational Geometry and Topology University of Nice Sophia Antipolis January 23-27, 2017 Computational Geometry and Topology
Lecture 1 Discrete Geometric Structures Jean-Daniel Boissonnat Winter School on Computational Geometry and Topology University of Nice Sophia Antipolis January 23-27, 2017 Computational Geometry and Topology
Mesh Generation through Delaunay Refinement
 Mesh Generation through Delaunay Refinement 3D Meshes Mariette Yvinec MPRI 2009-2010, C2-14-1, Lecture 4b ENSL Winter School, january 2010 Input : C : a 2D PLC in R 3 (piecewise linear complex) Ω : a bounded
Mesh Generation through Delaunay Refinement 3D Meshes Mariette Yvinec MPRI 2009-2010, C2-14-1, Lecture 4b ENSL Winter School, january 2010 Input : C : a 2D PLC in R 3 (piecewise linear complex) Ω : a bounded
Correctness. The Powercrust Algorithm for Surface Reconstruction. Correctness. Correctness. Delaunay Triangulation. Tools - Voronoi Diagram
 Correctness The Powercrust Algorithm for Surface Reconstruction Nina Amenta Sunghee Choi Ravi Kolluri University of Texas at Austin Boundary of a solid Close to original surface Homeomorphic to original
Correctness The Powercrust Algorithm for Surface Reconstruction Nina Amenta Sunghee Choi Ravi Kolluri University of Texas at Austin Boundary of a solid Close to original surface Homeomorphic to original
VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells
 VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells Scott A. Mitchell (speaker), joint work with Ahmed H. Mahmoud, Ahmad A. Rushdi, Scott A. Mitchell, Ahmad Abdelkader
VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells Scott A. Mitchell (speaker), joint work with Ahmed H. Mahmoud, Ahmad A. Rushdi, Scott A. Mitchell, Ahmad Abdelkader
A Fast and Simple Surface Reconstruction Algorithm
 A Fast and Simple Surface Reconstruction Algorithm Siu-Wing Cheng Jiongxin Jin Man-Kit Lau Abstract We present an algorithm for surface reconstruction from a point cloud. It runs in O(n log n) time, where
A Fast and Simple Surface Reconstruction Algorithm Siu-Wing Cheng Jiongxin Jin Man-Kit Lau Abstract We present an algorithm for surface reconstruction from a point cloud. It runs in O(n log n) time, where
Meshing Volumes Bounded by Smooth Surfaces
 Meshing Volumes Bounded by Smooth Surfaces Steve Oudot, Laurent Rineau, Mariette Yvinec To cite this version: Steve Oudot, Laurent Rineau, Mariette Yvinec. Meshing Volumes Bounded by Smooth Surfaces. International
Meshing Volumes Bounded by Smooth Surfaces Steve Oudot, Laurent Rineau, Mariette Yvinec To cite this version: Steve Oudot, Laurent Rineau, Mariette Yvinec. Meshing Volumes Bounded by Smooth Surfaces. International
Tiling Three-Dimensional Space with Simplices. Shankar Krishnan AT&T Labs - Research
 Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
The Medial Axis of the Union of Inner Voronoi Balls in the Plane
 The Medial Axis of the Union of Inner Voronoi Balls in the Plane Joachim Giesen a, Balint Miklos b,, Mark Pauly b a Max-Planck Institut für Informatik, Saarbrücken, Germany b Applied Geometry Group, ETH
The Medial Axis of the Union of Inner Voronoi Balls in the Plane Joachim Giesen a, Balint Miklos b,, Mark Pauly b a Max-Planck Institut für Informatik, Saarbrücken, Germany b Applied Geometry Group, ETH
An Analysis of Shewchuk s Delaunay Refinement Algorithm
 An Analysis of Shewchuk s Delaunay Refinement Algorithm Hang Si Weierstrass Institute for Applied Analysis and Stochastics (WIAS), Berlin si@wias-berlin.de Summary. Shewchuk s Delaunay refinement algorithm
An Analysis of Shewchuk s Delaunay Refinement Algorithm Hang Si Weierstrass Institute for Applied Analysis and Stochastics (WIAS), Berlin si@wias-berlin.de Summary. Shewchuk s Delaunay refinement algorithm
Coxeter triangulations have good quality
 Coxeter triangulations have good quality Aruni Choudhary, Siargey Kachanovich, and Mathijs Wintraecken Max Planck Institute for Informatics, Saarland Informatics Campus Saarbrücken, Germany Université
Coxeter triangulations have good quality Aruni Choudhary, Siargey Kachanovich, and Mathijs Wintraecken Max Planck Institute for Informatics, Saarland Informatics Campus Saarbrücken, Germany Université
High-Quality Consistent Meshing of Multi-Label Datasets
 High-Quality Consistent Meshing of Multi-Label Datasets Jean-Philippe Pons, Florent Ségonne, Jean-Daniel Boissonnat, Laurent Rineau, Mariette Yvinec, Renaud Keriven To cite this version: Jean-Philippe
High-Quality Consistent Meshing of Multi-Label Datasets Jean-Philippe Pons, Florent Ségonne, Jean-Daniel Boissonnat, Laurent Rineau, Mariette Yvinec, Renaud Keriven To cite this version: Jean-Philippe
Lecture 3 Randomized Algorithms
 Lecture 3 Randomized Algorithms Jean-Daniel Boissonnat Winter School on Computational Geometry and Topology University of Nice Sophia Antipolis January 23-27, 2017 Computational Geometry and Topology Randomized
Lecture 3 Randomized Algorithms Jean-Daniel Boissonnat Winter School on Computational Geometry and Topology University of Nice Sophia Antipolis January 23-27, 2017 Computational Geometry and Topology Randomized
Surface Reconstruction with MLS
 Surface Reconstruction with MLS Tobias Martin CS7960, Spring 2006, Feb 23 Literature An Adaptive MLS Surface for Reconstruction with Guarantees, T. K. Dey and J. Sun A Sampling Theorem for MLS Surfaces,
Surface Reconstruction with MLS Tobias Martin CS7960, Spring 2006, Feb 23 Literature An Adaptive MLS Surface for Reconstruction with Guarantees, T. K. Dey and J. Sun A Sampling Theorem for MLS Surfaces,
Voronoi Diagram. Xiao-Ming Fu
 Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Isotopic Approximation within a Tolerance Volume
 Isotopic Approximation within a Tolerance Volume Manish Mandad David Cohen-Steiner Pierre Alliez Inria Sophia Antipolis - 1 Goals and Motivation - 2 Goals and Motivation Input: Tolerance volume of a surface
Isotopic Approximation within a Tolerance Volume Manish Mandad David Cohen-Steiner Pierre Alliez Inria Sophia Antipolis - 1 Goals and Motivation - 2 Goals and Motivation Input: Tolerance volume of a surface
Dynamic Mesh Refinement
 Dynamic Mesh Refinement Benoît Hudson Joint work with Umut A. Acar, Gary Miller, Todd Phillips Why Mesh? Geometry is continuous Computers are discrete Graphics Scientific Computing Vision, AI,... Mesh
Dynamic Mesh Refinement Benoît Hudson Joint work with Umut A. Acar, Gary Miller, Todd Phillips Why Mesh? Geometry is continuous Computers are discrete Graphics Scientific Computing Vision, AI,... Mesh
Introduction to Computer Graphics. Modeling (3) April 27, 2017 Kenshi Takayama
 Introduction to Computer Graphics Modeling (3) April 27, 2017 Kenshi Takayama Solid modeling 2 Solid models Thin shapes represented by single polygons Unorientable Clear definition of inside & outside
Introduction to Computer Graphics Modeling (3) April 27, 2017 Kenshi Takayama Solid modeling 2 Solid models Thin shapes represented by single polygons Unorientable Clear definition of inside & outside
Outline. Reconstruction of 3D Meshes from Point Clouds. Motivation. Problem Statement. Applications. Challenges
 Reconstruction of 3D Meshes from Point Clouds Ming Zhang Patrick Min cs598b, Geometric Modeling for Computer Graphics Feb. 17, 2000 Outline - problem statement - motivation - applications - challenges
Reconstruction of 3D Meshes from Point Clouds Ming Zhang Patrick Min cs598b, Geometric Modeling for Computer Graphics Feb. 17, 2000 Outline - problem statement - motivation - applications - challenges
Complex conforming Delaunay triangulation
 . RESEARCH PAPERS. SCIENCE CHINA Information Sciences June 2010 Vol. 53 No. 6: 1130 1140 doi: 10.1007/s11432-010-0097-6 Complex conforming Delaunay triangulation MENG XianHai 1, LI JiGang 1, YANG Qin 1,
. RESEARCH PAPERS. SCIENCE CHINA Information Sciences June 2010 Vol. 53 No. 6: 1130 1140 doi: 10.1007/s11432-010-0097-6 Complex conforming Delaunay triangulation MENG XianHai 1, LI JiGang 1, YANG Qin 1,
Critical Points of the Distance to an epsilon-sampling of a Surface and Flow-Complex-Based Surface Reconstruction
 Critical Points of the Distance to an epsilon-sampling of a Surface and Flow-Complex-Based Surface Reconstruction Tamal K. Dey Department of CSE Joachim Giesen Theoretische Informatik Edgar A. Ramos Dept.
Critical Points of the Distance to an epsilon-sampling of a Surface and Flow-Complex-Based Surface Reconstruction Tamal K. Dey Department of CSE Joachim Giesen Theoretische Informatik Edgar A. Ramos Dept.
Computational Geometry. Algorithm Design (10) Computational Geometry. Convex Hull. Areas in Computational Geometry
 Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
Smooth Surface Reconstruction from Noisy Clouds
 Smooth Surface Reconstruction from Noisy Clouds Boris Mederos, Luiz Velho and Luiz Henrique de Figueiredo IMPA Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina 110, 22461-320 Rio de Janeiro,
Smooth Surface Reconstruction from Noisy Clouds Boris Mederos, Luiz Velho and Luiz Henrique de Figueiredo IMPA Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina 110, 22461-320 Rio de Janeiro,
Outline of the presentation
 Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass
 Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Approximating Geodesic Distances on 2-Manifolds in R 3
 CCCG 2011, Toronto ON, August 10 12, 2011 Approximating Geodesic Distances on 2-Manifolds in R 3 Christian Scheffer Jan Vahrenhold Abstract We present an algorithm for approximating geodesic distances
CCCG 2011, Toronto ON, August 10 12, 2011 Approximating Geodesic Distances on 2-Manifolds in R 3 Christian Scheffer Jan Vahrenhold Abstract We present an algorithm for approximating geodesic distances
Computational Geometry
 Lecture 12: Lecture 12: Motivation: Terrains by interpolation To build a model of the terrain surface, we can start with a number of sample points where we know the height. Lecture 12: Motivation: Terrains
Lecture 12: Lecture 12: Motivation: Terrains by interpolation To build a model of the terrain surface, we can start with a number of sample points where we know the height. Lecture 12: Motivation: Terrains
Reconstruction of Filament Structure
 Reconstruction of Filament Structure Ruqi HUANG INRIA-Geometrica Joint work with Frédéric CHAZAL and Jian SUN 27/10/2014 Outline 1 Problem Statement Characterization of Dataset Formulation 2 Our Approaches
Reconstruction of Filament Structure Ruqi HUANG INRIA-Geometrica Joint work with Frédéric CHAZAL and Jian SUN 27/10/2014 Outline 1 Problem Statement Characterization of Dataset Formulation 2 Our Approaches
A Multicover Nerve for Geometric Inference. Don Sheehy INRIA Saclay, France
 A Multicover Nerve for Geometric Inference Don Sheehy INRIA Saclay, France Computational geometers use topology to certify geometric constructions. Computational geometers use topology to certify geometric
A Multicover Nerve for Geometric Inference Don Sheehy INRIA Saclay, France Computational geometers use topology to certify geometric constructions. Computational geometers use topology to certify geometric
Meshing Skin Surfaces with Certified Topology
 Meshing Skin Surfaces with Certified Topology Nico Kruithof and Gert Vegter Department of Mathematics and Computing Science University of Groningen, The Netherlands {nico,gert}@cs.rug.nl Abstract We present
Meshing Skin Surfaces with Certified Topology Nico Kruithof and Gert Vegter Department of Mathematics and Computing Science University of Groningen, The Netherlands {nico,gert}@cs.rug.nl Abstract We present
Computational Geometry
 Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Voronoi diagrams Delaunay Triangulations. Pierre Alliez Inria
 Voronoi diagrams Delaunay Triangulations Pierre Alliez Inria Voronoi Diagram Voronoi Diagram Voronoi Diagram The collection of the non-empty Voronoi regions and their faces, together with their incidence
Voronoi diagrams Delaunay Triangulations Pierre Alliez Inria Voronoi Diagram Voronoi Diagram Voronoi Diagram The collection of the non-empty Voronoi regions and their faces, together with their incidence
New Results on the Stability of Persistence Diagrams
 New Results on the Stability of Persistence Diagrams Primoz Skraba Jozef Stefan Institute TAGS - Linking Topology to Algebraic Geometry and Statistics joint work with Katharine Turner and D. Yogeshwaran
New Results on the Stability of Persistence Diagrams Primoz Skraba Jozef Stefan Institute TAGS - Linking Topology to Algebraic Geometry and Statistics joint work with Katharine Turner and D. Yogeshwaran
Quality Meshing for Polyhedra with Small Angles
 Quality Meshing for Polyhedra with Small Angles Siu-Wing Cheng Tamal K. Dey Edgar A. Ramos Tathagata Ray April 11, 2005 Abstract We present an algorithm to compute a Delaunay mesh conforming to a polyhedron
Quality Meshing for Polyhedra with Small Angles Siu-Wing Cheng Tamal K. Dey Edgar A. Ramos Tathagata Ray April 11, 2005 Abstract We present an algorithm to compute a Delaunay mesh conforming to a polyhedron
Delaunay Refinement by Corner Lopping
 Delaunay Refinement by Corner Lopping Steven E. Pav 1 and Noel J. Walkington 2 1 University of California at San Diego, La Jolla, CA. spav@ucsd.edu 2 Carnegie Mellon University, Pittsburgh, PA. noelw@andrew.cmu.edu
Delaunay Refinement by Corner Lopping Steven E. Pav 1 and Noel J. Walkington 2 1 University of California at San Diego, La Jolla, CA. spav@ucsd.edu 2 Carnegie Mellon University, Pittsburgh, PA. noelw@andrew.cmu.edu
Approximating Polygonal Objects by Deformable Smooth Surfaces
 Approximating Polygonal Objects by Deformable Smooth Surfaces Ho-lun Cheng and Tony Tan School of Computing, National University of Singapore hcheng,tantony@comp.nus.edu.sg Abstract. We propose a method
Approximating Polygonal Objects by Deformable Smooth Surfaces Ho-lun Cheng and Tony Tan School of Computing, National University of Singapore hcheng,tantony@comp.nus.edu.sg Abstract. We propose a method
Conforming Delaunay triangulations in 3D
 Computational Geometry 28 (2004) 217 233 www.elsevier.com/locate/comgeo Conforming Delaunay triangulations in 3D David Cohen-Steiner a, Éric Colin de Verdière b,, Mariette Yvinec a a INRIA, Sophia-Antipolis,
Computational Geometry 28 (2004) 217 233 www.elsevier.com/locate/comgeo Conforming Delaunay triangulations in 3D David Cohen-Steiner a, Éric Colin de Verdière b,, Mariette Yvinec a a INRIA, Sophia-Antipolis,
03 - Reconstruction. Acknowledgements: Olga Sorkine-Hornung. CSCI-GA Geometric Modeling - Spring 17 - Daniele Panozzo
 3 - Reconstruction Acknowledgements: Olga Sorkine-Hornung Geometry Acquisition Pipeline Scanning: results in range images Registration: bring all range images to one coordinate system Stitching/ reconstruction:
3 - Reconstruction Acknowledgements: Olga Sorkine-Hornung Geometry Acquisition Pipeline Scanning: results in range images Registration: bring all range images to one coordinate system Stitching/ reconstruction:
Lecture 2 Unstructured Mesh Generation
 Lecture 2 Unstructured Mesh Generation MIT 16.930 Advanced Topics in Numerical Methods for Partial Differential Equations Per-Olof Persson (persson@mit.edu) February 13, 2006 1 Mesh Generation Given a
Lecture 2 Unstructured Mesh Generation MIT 16.930 Advanced Topics in Numerical Methods for Partial Differential Equations Per-Olof Persson (persson@mit.edu) February 13, 2006 1 Mesh Generation Given a
Complexity of Delaunay triangulation for points on lower-dimensional polyhedra
 Complexity of Delaunay triangulation for points on lower-dimensional polyhedra Nina Amenta UC Davis Dominique Attali CNRS-LIS Grenoble Olivier Devillers INRIA Sophia-Antipolis Abstract We show that the
Complexity of Delaunay triangulation for points on lower-dimensional polyhedra Nina Amenta UC Davis Dominique Attali CNRS-LIS Grenoble Olivier Devillers INRIA Sophia-Antipolis Abstract We show that the
A THINNING ALGORITHM FOR TOPOLOGICALLY CORRECT 3D SURFACE RECONSTRUCTION
 A THINNING ALGORITHM FOR TOPOLOGICALLY CORRECT 3D SURFACE RECONSTRUCTION Leonid Tcherniavski Department of Informatics University of Hamburg tcherniavski@informatik.uni-hamburg.de ABSTRACT The existing
A THINNING ALGORITHM FOR TOPOLOGICALLY CORRECT 3D SURFACE RECONSTRUCTION Leonid Tcherniavski Department of Informatics University of Hamburg tcherniavski@informatik.uni-hamburg.de ABSTRACT The existing
A flexible framework for surface reconstruction from large point sets
 A flexible framework for surface reconstruction from large point sets Rémi Allègre, Raphaëlle Chaine, Samir Akkouche LIRIS UMR 5205 CNRS / Université Lyon 1, Villeurbanne, F-69622, France Abstract This
A flexible framework for surface reconstruction from large point sets Rémi Allègre, Raphaëlle Chaine, Samir Akkouche LIRIS UMR 5205 CNRS / Université Lyon 1, Villeurbanne, F-69622, France Abstract This
Three-Dimensional Delaunay Mesh Generation
 Three-Dimensional Delaunay Mesh Generation Siu-Wing Cheng Sheung-Hung Poon February 20, 2004 Abstract We propose an algorithm to compute a conforming Delaunay mesh of a bounded domain specified by a piecewise
Three-Dimensional Delaunay Mesh Generation Siu-Wing Cheng Sheung-Hung Poon February 20, 2004 Abstract We propose an algorithm to compute a conforming Delaunay mesh of a bounded domain specified by a piecewise
Surface Reconstruction. Gianpaolo Palma
 Surface Reconstruction Gianpaolo Palma Surface reconstruction Input Point cloud With or without normals Examples: multi-view stereo, union of range scan vertices Range scans Each scan is a triangular mesh
Surface Reconstruction Gianpaolo Palma Surface reconstruction Input Point cloud With or without normals Examples: multi-view stereo, union of range scan vertices Range scans Each scan is a triangular mesh
Mesh generation from 3D multi-material images
 Mesh generation from 3D multi-material images Dobrina Boltcheva, Mariette Yvinec, Jean-Daniel Boissonnat To cite this version: Dobrina Boltcheva, Mariette Yvinec, Jean-Daniel Boissonnat. Mesh generation
Mesh generation from 3D multi-material images Dobrina Boltcheva, Mariette Yvinec, Jean-Daniel Boissonnat To cite this version: Dobrina Boltcheva, Mariette Yvinec, Jean-Daniel Boissonnat. Mesh generation
Scientific Computing WS 2018/2019. Lecture 12. Jürgen Fuhrmann Lecture 12 Slide 1
 Scientific Computing WS 2018/2019 Lecture 12 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 12 Slide 1 Recap For more discussion of mesh generation, see J.R. Shewchuk: Lecture Notes on Delaunay
Scientific Computing WS 2018/2019 Lecture 12 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 12 Slide 1 Recap For more discussion of mesh generation, see J.R. Shewchuk: Lecture Notes on Delaunay
Surface Reconstruction
 Eurographics Symposium on Geometry Processing (2006) Surface Reconstruction 2009.12.29 Some methods for surface reconstruction Classification 1. Based on Delaunay triangulation(or Voronoi diagram) Alpha
Eurographics Symposium on Geometry Processing (2006) Surface Reconstruction 2009.12.29 Some methods for surface reconstruction Classification 1. Based on Delaunay triangulation(or Voronoi diagram) Alpha
Survey of Surface Reconstruction Algorithms
 Journal of Signal and Information Processing, 2014, 5, 63-79 Published Online August 2014 in SciRes. http://www.scirp.org/journal/jsip http://dx.doi.org/10.4236/jsip.2014.53009 Survey of Surface Reconstruction
Journal of Signal and Information Processing, 2014, 5, 63-79 Published Online August 2014 in SciRes. http://www.scirp.org/journal/jsip http://dx.doi.org/10.4236/jsip.2014.53009 Survey of Surface Reconstruction
Localized Delaunay Refinement for Volumes
 Eurographics Symposium on Geometry Processing 2011 Mario Botsch and Scott Schaefer (Guest Editors) Volume 30 (2011), Number 5 Localized Delaunay Refinement for Volumes Tamal K Dey 1 and Andrew G Slatton
Eurographics Symposium on Geometry Processing 2011 Mario Botsch and Scott Schaefer (Guest Editors) Volume 30 (2011), Number 5 Localized Delaunay Refinement for Volumes Tamal K Dey 1 and Andrew G Slatton
Simplicial Hyperbolic Surfaces
 Simplicial Hyperbolic Surfaces Talk by Ken Bromberg August 21, 2007 1-Lipschitz Surfaces- In this lecture we will discuss geometrically meaningful ways of mapping a surface S into a hyperbolic manifold
Simplicial Hyperbolic Surfaces Talk by Ken Bromberg August 21, 2007 1-Lipschitz Surfaces- In this lecture we will discuss geometrically meaningful ways of mapping a surface S into a hyperbolic manifold
Simplicial Complexes: Second Lecture
 Simplicial Complexes: Second Lecture 4 Nov, 2010 1 Overview Today we have two main goals: Prove that every continuous map between triangulable spaces can be approximated by a simplicial map. To do this,
Simplicial Complexes: Second Lecture 4 Nov, 2010 1 Overview Today we have two main goals: Prove that every continuous map between triangulable spaces can be approximated by a simplicial map. To do this,
On the Locality of Extracting a 2-Manifold in IR 3
 On the Locality of Extracting a 2-Manifold in IR 3 Daniel Dumitriu 1, Stefan Funke 2, Martin Kutz, and Nikola Milosavljević 3 1 Max-Planck-Institut für Informatik Campus E 1.4, 66123 Saarbrücken, Germany
On the Locality of Extracting a 2-Manifold in IR 3 Daniel Dumitriu 1, Stefan Funke 2, Martin Kutz, and Nikola Milosavljević 3 1 Max-Planck-Institut für Informatik Campus E 1.4, 66123 Saarbrücken, Germany
Surface segmentation for improved isotropic remeshing
 J. Edwards (Univ. of Texas) IMR 2012 1 / 20 Surface segmentation for improved isotropic remeshing John Edwards, Wenping Wang, Chandrajit Bajaj Department of Computer Science The University of Texas at
J. Edwards (Univ. of Texas) IMR 2012 1 / 20 Surface segmentation for improved isotropic remeshing John Edwards, Wenping Wang, Chandrajit Bajaj Department of Computer Science The University of Texas at
Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls
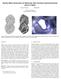 Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls Ho-Lun Cheng Xinwei Shi School of Computing National University of Singapore Figure 1: Molecular models of the molecule
Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls Ho-Lun Cheng Xinwei Shi School of Computing National University of Singapore Figure 1: Molecular models of the molecule
Scalar Algorithms: Contouring
 Scalar Algorithms: Contouring Computer Animation and Visualisation Lecture tkomura@inf.ed.ac.uk Institute for Perception, Action & Behaviour School of Informatics Contouring Scaler Data Last Lecture...
Scalar Algorithms: Contouring Computer Animation and Visualisation Lecture tkomura@inf.ed.ac.uk Institute for Perception, Action & Behaviour School of Informatics Contouring Scaler Data Last Lecture...
Hang Si. Weierstrass Institute for Applied Analysis and Stochastics Berlin, Germany. Tetrahedron II
 W eierstraß-institut für Angew andte Analysis und Stochastik 3D Boundary Recovery and Constrained Delaunay Tetrahedralizations Hang Si Weierstrass Institute for Applied Analysis and Stochastics Berlin,
W eierstraß-institut für Angew andte Analysis und Stochastik 3D Boundary Recovery and Constrained Delaunay Tetrahedralizations Hang Si Weierstrass Institute for Applied Analysis and Stochastics Berlin,
Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image
 to appear in IEEE PAMI Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image Peer Stelldinger, Longin Jan Latecki and Marcelo Siqueira Abstract Digitization is not as
to appear in IEEE PAMI Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image Peer Stelldinger, Longin Jan Latecki and Marcelo Siqueira Abstract Digitization is not as
Isotopic Approximation of Implicit Curves and Surfaces (Extended Abstract)
 Isotopic Approximation of Implicit Curves and Surfaces (Extended Abstract) Simon Plantinga and Gert Vegter Institute for Mathematics and Computing Science University of Groningen simon@cs.rug.nl gert@cs.rug.nl
Isotopic Approximation of Implicit Curves and Surfaces (Extended Abstract) Simon Plantinga and Gert Vegter Institute for Mathematics and Computing Science University of Groningen simon@cs.rug.nl gert@cs.rug.nl
Surface reconstruction based on a dynamical system
 EUROGRAPHICS 2002 / G. Drettakis and H.-P. Seidel (Guest Editors) Volume 21 (2002), Number 3 Surface reconstruction based on a dynamical system N.N. Abstract We present an efficient algorithm that computes
EUROGRAPHICS 2002 / G. Drettakis and H.-P. Seidel (Guest Editors) Volume 21 (2002), Number 3 Surface reconstruction based on a dynamical system N.N. Abstract We present an efficient algorithm that computes
Kurt Mehlhorn, MPI für Informatik. Curve and Surface Reconstruction p.1/25
 Curve and Surface Reconstruction Kurt Mehlhorn MPI für Informatik Curve and Surface Reconstruction p.1/25 Curve Reconstruction: An Example probably, you see more than a set of points Curve and Surface
Curve and Surface Reconstruction Kurt Mehlhorn MPI für Informatik Curve and Surface Reconstruction p.1/25 Curve Reconstruction: An Example probably, you see more than a set of points Curve and Surface
Computational Geometry Lecture Delaunay Triangulation
 Computational Geometry Lecture Delaunay Triangulation INSTITUTE FOR THEORETICAL INFORMATICS FACULTY OF INFORMATICS 7.12.2015 1 Modelling a Terrain Sample points p = (x p, y p, z p ) Projection π(p) = (p
Computational Geometry Lecture Delaunay Triangulation INSTITUTE FOR THEORETICAL INFORMATICS FACULTY OF INFORMATICS 7.12.2015 1 Modelling a Terrain Sample points p = (x p, y p, z p ) Projection π(p) = (p
Advanced Algorithms Computational Geometry Prof. Karen Daniels. Fall, 2012
 UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Fall, 2012 Voronoi Diagrams & Delaunay Triangulations O Rourke: Chapter 5 de Berg et al.: Chapters 7,
UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Fall, 2012 Voronoi Diagrams & Delaunay Triangulations O Rourke: Chapter 5 de Berg et al.: Chapters 7,
Möbius Transformations in Scientific Computing. David Eppstein
 Möbius Transformations in Scientific Computing David Eppstein Univ. of California, Irvine School of Information and Computer Science (including joint work with Marshall Bern from WADS 01 and SODA 03) Outline
Möbius Transformations in Scientific Computing David Eppstein Univ. of California, Irvine School of Information and Computer Science (including joint work with Marshall Bern from WADS 01 and SODA 03) Outline
Complexity of Delaunay Triangulation for Points on Lower-dimensional Polyhedra.
 published in Proc. 18th ACM-SIAM Sympos. Discrete Algorithms (SODA) 2007, p.1106 1113. Complexity of Delaunay Triangulation for Points on Lower-dimensional Polyhedra. Nina Amenta UC Davis Dominique Attali
published in Proc. 18th ACM-SIAM Sympos. Discrete Algorithms (SODA) 2007, p.1106 1113. Complexity of Delaunay Triangulation for Points on Lower-dimensional Polyhedra. Nina Amenta UC Davis Dominique Attali
Planar Graphs. 1 Graphs and maps. 1.1 Planarity and duality
 Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Discrete representations of geometric objects: Features, data structures and adequacy for dynamic simulation. Part I : Solid geometry
 Discrete representations of geometric objects: Features, data structures and adequacy for dynamic simulation. Surfaces Part I : Solid geometry hachar Fleishman Tel Aviv University David Levin Claudio T.
Discrete representations of geometric objects: Features, data structures and adequacy for dynamic simulation. Surfaces Part I : Solid geometry hachar Fleishman Tel Aviv University David Levin Claudio T.
As a consequence of the operation, there are new incidences between edges and triangles that did not exist in K; see Figure II.9.
 II.4 Surface Simplification 37 II.4 Surface Simplification In applications it is often necessary to simplify the data or its representation. One reason is measurement noise, which we would like to eliminate,
II.4 Surface Simplification 37 II.4 Surface Simplification In applications it is often necessary to simplify the data or its representation. One reason is measurement noise, which we would like to eliminate,
Interpolating and Approximating Implicit Surfaces from Polygon Soup
 Interpolating and Approimating Implicit Surfaces from Polygon Soup Chen Shen, James F. O Brien, Jonathan R. Shewchuk University of California, Berkeley Geometric Algorithms Seminar CS 468 Fall 2005 Overview
Interpolating and Approimating Implicit Surfaces from Polygon Soup Chen Shen, James F. O Brien, Jonathan R. Shewchuk University of California, Berkeley Geometric Algorithms Seminar CS 468 Fall 2005 Overview
Acute Triangulations of Polygons
 Europ. J. Combinatorics (2002) 23, 45 55 doi:10.1006/eujc.2001.0531 Available online at http://www.idealibrary.com on Acute Triangulations of Polygons H. MAEHARA We prove that every n-gon can be triangulated
Europ. J. Combinatorics (2002) 23, 45 55 doi:10.1006/eujc.2001.0531 Available online at http://www.idealibrary.com on Acute Triangulations of Polygons H. MAEHARA We prove that every n-gon can be triangulated
B.Stat / B.Math. Entrance Examination 2017
 B.Stat / B.Math. Entrance Examination 017 BOOKLET NO. TEST CODE : UGA Forenoon Questions : 0 Time : hours Write your Name, Registration Number, Test Centre, Test Code and the Number of this Booklet in
B.Stat / B.Math. Entrance Examination 017 BOOKLET NO. TEST CODE : UGA Forenoon Questions : 0 Time : hours Write your Name, Registration Number, Test Centre, Test Code and the Number of this Booklet in
CS 468, Spring 2013 Differential Geometry for Computer Science Justin Solomon and Adrian Butscher
 http://alice.loria.fr/index.php/publications.html?redirect=0&paper=vsdm@2011&author=levy CS 468, Spring 2013 Differential Geometry for Computer Science Justin Solomon and Adrian Butscher µ R 3 µ R 2 http://upload.wikimedia.org/wikipedia/commons/b/bc/double_torus_illustration.png
http://alice.loria.fr/index.php/publications.html?redirect=0&paper=vsdm@2011&author=levy CS 468, Spring 2013 Differential Geometry for Computer Science Justin Solomon and Adrian Butscher µ R 3 µ R 2 http://upload.wikimedia.org/wikipedia/commons/b/bc/double_torus_illustration.png
SURFACE RECONSTRUCTION AND SIMPLIFICATION
 NATIONAL AND KAPODISTRIAN UNIVERSITY OF ATHENS DEPARTMENT OF INFORMATICS AND TELECOMMUNICATIOS SECTOR OF THEORETICAL INFORMATICS SURFACE RECONSTRUCTION AND SIMPLIFICATION Alexander Agathos Master Thesis
NATIONAL AND KAPODISTRIAN UNIVERSITY OF ATHENS DEPARTMENT OF INFORMATICS AND TELECOMMUNICATIOS SECTOR OF THEORETICAL INFORMATICS SURFACE RECONSTRUCTION AND SIMPLIFICATION Alexander Agathos Master Thesis
Computational Geometry Learning
 Computational Geometry Learning Jean-Daniel Boissonnat Frédéric Chazal Geometrica, INRIA http://www-sop.inria.fr/geometrica Lectures at MPRI MPRI Computational Geometry Learning Lectures at MPRI 1 / 14
Computational Geometry Learning Jean-Daniel Boissonnat Frédéric Chazal Geometrica, INRIA http://www-sop.inria.fr/geometrica Lectures at MPRI MPRI Computational Geometry Learning Lectures at MPRI 1 / 14
Quadrilateral Meshing by Circle Packing
 Quadrilateral Meshing by Circle Packing Marshall Bern 1 David Eppstein 2 Abstract We use circle-packing methods to generate quadrilateral meshes for polygonal domains, with guaranteed bounds both on the
Quadrilateral Meshing by Circle Packing Marshall Bern 1 David Eppstein 2 Abstract We use circle-packing methods to generate quadrilateral meshes for polygonal domains, with guaranteed bounds both on the
A Simple Algorithm for Homeomorphic Surface Reconstruction
 A Simple Algorithm for Homeomorphic Surface Reconstruction N. Amenta* S. Choit T.K. Dey ~ N. Leekha Abstract 1 Introduction The problem of computing a piecewise linear approximation to a surface from a
A Simple Algorithm for Homeomorphic Surface Reconstruction N. Amenta* S. Choit T.K. Dey ~ N. Leekha Abstract 1 Introduction The problem of computing a piecewise linear approximation to a surface from a
Topological Inference via Meshing
 Topological Inference via Meshing Benoit Hudson, Gary Miller, Steve Oudot and Don Sheehy SoCG 2010 Mesh Generation and Persistent Homology The Problem Input: Points in Euclidean space sampled from some
Topological Inference via Meshing Benoit Hudson, Gary Miller, Steve Oudot and Don Sheehy SoCG 2010 Mesh Generation and Persistent Homology The Problem Input: Points in Euclidean space sampled from some
Spatio-Temporal Shape from Silhouette using Four-Dimensional Delaunay Meshing
 Spatio-Temporal Shape from Silhouette using Four-Dimensional Delaunay Meshing Ehsan Aganj, Jean-Philippe Pons, Florent Ségonne and Renaud Keriven WILLOW Team, CERTIS, École des ponts Marne-la-Vallée, France
Spatio-Temporal Shape from Silhouette using Four-Dimensional Delaunay Meshing Ehsan Aganj, Jean-Philippe Pons, Florent Ségonne and Renaud Keriven WILLOW Team, CERTIS, École des ponts Marne-la-Vallée, France
Voronoi diagram and Delaunay triangulation
 Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Topological Inference via Meshing
 Topological Inference via Meshing Don Sheehy Theory Lunch Joint work with Benoit Hudson, Gary Miller, and Steve Oudot Computer Scientists want to know the shape of data. Clustering Principal Component
Topological Inference via Meshing Don Sheehy Theory Lunch Joint work with Benoit Hudson, Gary Miller, and Steve Oudot Computer Scientists want to know the shape of data. Clustering Principal Component
Optimal Compression of a Polyline with Segments and Arcs
 Optimal Compression of a Polyline with Segments and Arcs Alexander Gribov Esri 380 New York Street Redlands, CA 92373 Email: agribov@esri.com arxiv:1604.07476v5 [cs.cg] 10 Apr 2017 Abstract This paper
Optimal Compression of a Polyline with Segments and Arcs Alexander Gribov Esri 380 New York Street Redlands, CA 92373 Email: agribov@esri.com arxiv:1604.07476v5 [cs.cg] 10 Apr 2017 Abstract This paper
Smooth surface reconstruction via natural neighbour interpolation of distance functions
 Computational Geometry 22 (2002) 185 203 www.elsevier.com/locate/comgeo Smooth surface reconstruction via natural neighbour interpolation of distance functions Jean-Daniel Boissonnat, Frédéric Cazals INRIA,
Computational Geometry 22 (2002) 185 203 www.elsevier.com/locate/comgeo Smooth surface reconstruction via natural neighbour interpolation of distance functions Jean-Daniel Boissonnat, Frédéric Cazals INRIA,
Topological Issues in Hexahedral Meshing
 Topological Issues in Hexahedral Meshing David Eppstein Univ. of California, Irvine Dept. of Information and Computer Science Outline I. What is meshing? Problem statement Types of mesh Quality issues
Topological Issues in Hexahedral Meshing David Eppstein Univ. of California, Irvine Dept. of Information and Computer Science Outline I. What is meshing? Problem statement Types of mesh Quality issues
Topological Data Analysis - I. Afra Zomorodian Department of Computer Science Dartmouth College
 Topological Data Analysis - I Afra Zomorodian Department of Computer Science Dartmouth College September 3, 2007 1 Acquisition Vision: Images (2D) GIS: Terrains (3D) Graphics: Surfaces (3D) Medicine: MRI
Topological Data Analysis - I Afra Zomorodian Department of Computer Science Dartmouth College September 3, 2007 1 Acquisition Vision: Images (2D) GIS: Terrains (3D) Graphics: Surfaces (3D) Medicine: MRI
Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder]
![Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder]](/thumbs/93/111713975.jpg) Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Preliminaries Recall: Given a smooth function f:r R, the function
Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Preliminaries Recall: Given a smooth function f:r R, the function
Chapter 10 Similarity
 Chapter 10 Similarity Def: The ratio of the number a to the number b is the number. A proportion is an equality between ratios. a, b, c, and d are called the first, second, third, and fourth terms. The
Chapter 10 Similarity Def: The ratio of the number a to the number b is the number. A proportion is an equality between ratios. a, b, c, and d are called the first, second, third, and fourth terms. The
Geometry Definitions and Theorems. Chapter 9. Definitions and Important Terms & Facts
 Geometry Definitions and Theorems Chapter 9 Definitions and Important Terms & Facts A circle is the set of points in a plane at a given distance from a given point in that plane. The given point is the
Geometry Definitions and Theorems Chapter 9 Definitions and Important Terms & Facts A circle is the set of points in a plane at a given distance from a given point in that plane. The given point is the
Course 16 Geometric Data Structures for Computer Graphics. Voronoi Diagrams
 Course 16 Geometric Data Structures for Computer Graphics Voronoi Diagrams Dr. Elmar Langetepe Institut für Informatik I Universität Bonn Geometric Data Structures for CG July 27 th Voronoi Diagrams San
Course 16 Geometric Data Structures for Computer Graphics Voronoi Diagrams Dr. Elmar Langetepe Institut für Informatik I Universität Bonn Geometric Data Structures for CG July 27 th Voronoi Diagrams San
Theoretical Computer Science. Anisotropic diagrams: Labelle Shewchuk approach revisited
 Theoretical Computer Science 408 (2008 163 173 Contents lists available at ScienceDirect Theoretical Computer Science journal homepage: www.elsevier.com/locate/tcs Anisotropic diagrams: Labelle Shewchuk
Theoretical Computer Science 408 (2008 163 173 Contents lists available at ScienceDirect Theoretical Computer Science journal homepage: www.elsevier.com/locate/tcs Anisotropic diagrams: Labelle Shewchuk
Periodic meshes for the CGAL library
 Periodic meshes for the CGAL library Aymeric Pellé, Monique Teillaud To cite this version: Aymeric Pellé, Monique Teillaud. Periodic meshes for the CGAL library. International Meshing Roundtable, Oct 2014,
Periodic meshes for the CGAL library Aymeric Pellé, Monique Teillaud To cite this version: Aymeric Pellé, Monique Teillaud. Periodic meshes for the CGAL library. International Meshing Roundtable, Oct 2014,
Heegaard splittings and virtual fibers
 Heegaard splittings and virtual fibers Joseph Maher maher@math.okstate.edu Oklahoma State University May 2008 Theorem: Let M be a closed hyperbolic 3-manifold, with a sequence of finite covers of bounded
Heegaard splittings and virtual fibers Joseph Maher maher@math.okstate.edu Oklahoma State University May 2008 Theorem: Let M be a closed hyperbolic 3-manifold, with a sequence of finite covers of bounded
Moving Least Squares Multiresolution Surface Approximation
 Moving Least Squares Multiresolution Surface Approximation BORIS MEDEROS LUIZ VELHO LUIZ HENRIQUE DE FIGUEIREDO IMPA Instituto de Matemática Pura e Aplicada Estrada Dona Castorina 110, 22461-320 Rio de
Moving Least Squares Multiresolution Surface Approximation BORIS MEDEROS LUIZ VELHO LUIZ HENRIQUE DE FIGUEIREDO IMPA Instituto de Matemática Pura e Aplicada Estrada Dona Castorina 110, 22461-320 Rio de
Outer Billiard on Piecewise Circular Curves & Piecewise Hyperbola Curves
 Outer Billiard on Piecewise Circular Curves & Piecewise Hyperbola Curves Brown University August 9, 2013 Outer Billiard ~ ~ p T 2 (p) T(p) Piecewise Circular Curves Definition Piecewise circular curve
Outer Billiard on Piecewise Circular Curves & Piecewise Hyperbola Curves Brown University August 9, 2013 Outer Billiard ~ ~ p T 2 (p) T(p) Piecewise Circular Curves Definition Piecewise circular curve
Unstructured Mesh Generation for Implicit Moving Geometries and Level Set Applications
 Unstructured Mesh Generation for Implicit Moving Geometries and Level Set Applications Per-Olof Persson (persson@mit.edu) Department of Mathematics Massachusetts Institute of Technology http://www.mit.edu/
Unstructured Mesh Generation for Implicit Moving Geometries and Level Set Applications Per-Olof Persson (persson@mit.edu) Department of Mathematics Massachusetts Institute of Technology http://www.mit.edu/
Multi-View Matching & Mesh Generation. Qixing Huang Feb. 13 th 2017
 Multi-View Matching & Mesh Generation Qixing Huang Feb. 13 th 2017 Geometry Reconstruction Pipeline RANSAC --- facts Sampling Feature point detection [Gelfand et al. 05, Huang et al. 06] Correspondences
Multi-View Matching & Mesh Generation Qixing Huang Feb. 13 th 2017 Geometry Reconstruction Pipeline RANSAC --- facts Sampling Feature point detection [Gelfand et al. 05, Huang et al. 06] Correspondences
Medial Scaffolds for 3D data modelling: status and challenges. Frederic Fol Leymarie
 Medial Scaffolds for 3D data modelling: status and challenges Frederic Fol Leymarie Outline Background Method and some algorithmic details Applications Shape representation: From the Medial Axis to the
Medial Scaffolds for 3D data modelling: status and challenges Frederic Fol Leymarie Outline Background Method and some algorithmic details Applications Shape representation: From the Medial Axis to the
