Formalising the Foundations of Geometry
|
|
|
- Cora Strickland
- 5 years ago
- Views:
Transcription
1 Formalising the March 27, 2015
2 Formalising Mathematics Why formalise? Because some proofs are too hard to verify by inspection (Kepler conjecture, Four-Colour Theorem, ABC conjecture) We need to contribute groundwork for such projects. To investigate new representations. To investigate ways to organise mathematics. To add case-studies, pushing our theorem provers. To investigate new automation for new domains. For historical insight into pre 20 th /21 st century mathematics.
3 The Euclid s Elements Earliest extant text on axiomatic geometry. possibly the most influential mathematical text ever written A system of ruler and compass constructions.
4 The Euclid s Elements Earliest extant text on axiomatic geometry. possibly the most influential mathematical text ever written A system of ruler and compass constructions. But, enables number theory, algebra, the theory of proportion, solid geometry and integration proofs to compute areas and volumes.
5 Euclid s Axioms elements.html 1. To draw a straight line from any point to any point. 2. To produce a finite straight line continuously in a straight line. 3. To describe a circle with any centre and radius. 4. That all right angles are equal to each other. 5. That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
6 Axiomatic Hilbert s most influential book on geometry in a hundred years 10 German editions. 2 English translations (last 1971). Truly formal: Beer mugs, tables and chairs. Now 22 axioms covering incidence of points of lines, ordering of points on a line, segments and angles defined as point pairs and intersecting lines and their congruence, a parallel axiom, the Archimedean axiom and a completeness axiom.
7 Formalisation and Machine-Verification In reviews:
8 Formalisation and Machine-Verification In reviews: Theoretically, at least, the deductions could be made without any reference to their content by the use of the ratiocinative calculus like that of Peano (,,, ) or a Jevons Logic machine. Veblen
9 Formalisation and Machine-Verification In reviews: Theoretically, at least, the deductions could be made without any reference to their content by the use of the ratiocinative calculus like that of Peano (,,, ) or a Jevons Logic machine. Veblen We might put the axioms into a reasoning apparatus like the logical machine of Stanley Jevons, and see all geometry come out of it. Poincaré
10 Formalisation and Machine-Verification This notion may seem artificial and peurile; and it is needless to point out how disastrous it would be in teaching and how hurtful to mental development; how deadening it would be for investigators, whose originality it would nip in the bud.
11 Formalisation and Machine-Verification I see in logistic only shackles for the inventor. It is no aid in conciseness far from it, and if twenty-seven equations were necessary to establish that 1 is a number, how many would be needed to prove a real theorem?
12 Hilbert s Primitives Consider three distinct sets of objects. Let the objects of the first set be called points [...]; let the objects of the second set be called lines ; let the objects of the third set be called planes.... The points, lines and planes are considered to have certain mutual relations and these relations are denoted by words like lie, between, [...] The precise and mathematically complete description of these relations follows from the axioms of geometry 1 For simplicity, we ll just formalise the planar fragment.
13 Hilbert s Primitives Consider three distinct sets of objects. Let the objects of the first set be called points [...]; let the objects of the second set be called lines ; let the objects of the third set be called planes.... The points, lines and planes are considered to have certain mutual relations and these relations are denoted by words like lie, between, [...] The precise and mathematically complete description of these relations follows from the axioms of geometry new type ("point",0) new type ("line",0) 1 1 For simplicity, we ll just formalise the planar fragment.
14 Hilbert s Primitives Consider three distinct sets of objects. Let the objects of the first set be called points [...]; let the objects of the second set be called lines ; let the objects of the third set be called planes.... The points, lines and planes are considered to have certain mutual relations and these relations are denoted by words like lie, between, [...] The precise and mathematically complete description of these relations follows from the axioms of geometry new type ("point",0) new type ("line",0) 1 new constant ("on line", :(point -> line -> bool) ) new constant ("between", :(point -> point -> point -> bool) ) 1 For simplicity, we ll just formalise the planar fragment.
15 Hilbert s axioms I, 1 For every two points A, B there exists a line a that contains each of the points A, B. I, 2 For every two points A, B there exits [sic] no more than one line that contains each of the points A, B. I, 3 There exist at least two points on a line. There exist at least three points that do not lie on a line.
16 Hilbert s axioms I, 1 For every two points A, B there exists a line a that contains each of the points A, B. I, 2 For every two points A, B there exits [sic] no more than one line that contains each of the points A, B. I, 3 There exist at least two points on a line. There exist at least three points that do not lie on a line. A B a. on line A a on line B a (I, 1) A B on line A a on line B a on line A b on line B b a = b (I, 2) A. B. A B on line A a on line B a (I, 3.1) A. B. C. ( a. on line A a on line B a on line C a) (I, 3.2)
17 Hilbert s axioms II, 1 If a point B lies between a point A and a point C then the points A, B, C are three distinct points of a line, and B then also lies between C and A. II, 2 For two points A and C, there always exists at least one point B on the line AC such that C lies between A and B. II, 3 Of any three points on a line there exists no more than one that lies between the other two.
18 Hilbert s axioms II, 1 If a point B lies between a point A and a point C then the points A, B, C are three distinct points of a line, and B then also lies between C and A. II, 2 For two points A and C, there always exists at least one point B on the line AC such that C lies between A and B. II, 3 Of any three points on a line there exists no more than one that lies between the other two. between A B C A C ( a. on line A a on line B a on line C a) between C B A (II, 1) A B C. between A B C (II, 2) between A B C between A C B (II, 3)
19 Hilbert s Axioms II, 4 Let A, B, C be three points that do not lie on a line and let a be a line in the plane ABC which does not meet any of the points A, B, C. If the line a passes through a point of the segment AB, it also passes through a point of the segment AC, or through a point of the segment BC. a E C E a F F A D B
20 First Proof THEOREM 3. For two points A and C there always exists at least one point D on the line AC that lies between A and C. PROOF. By Axiom I, 3 there exists a point E outside the line AC and by Axiom II, 2 there exists on AE a point F such that E is a point of the segment AF. By the same axiom and by Axiom II, 3 there exists on FC a point G that does not lie on the segment FC. By Axiom II, 4 the line EG must then intersect the segment AC at a point D. F E A D C G
21 Representation collinear : (point bool) bool def collinear Ps a. P. P Ps on line P a.
22 Representation collinear : (point bool) bool def collinear Ps a. P. P Ps on line P a. collinear {A, B} S T collinear T collinear S A B A, B S, T collinear S collinear T collinear (S T )
23 Representation collinear : (point bool) bool def collinear Ps a. P. P Ps on line P a. collinear {A, B} S T collinear T collinear S A B A, B S, T collinear S collinear T collinear (S T ) collinear S collinear T collinear U U S T A, B S, T A = B collinear S collinear {A, B, C} X, Y, A, B S X Y collinear {C, X, Y }
24 Pasch in collinear sets collinear {A, B, C} collinear {A, D, E} collinear {C, D, E} between A D B F. collinear {D, E, F } (between A F C between B F C). (II, 4)
25 Verification of Theorem 3 assume A C so consider E such that ( a. on line A a on line C a on line E a) by (I, 2), (I, 3.2) 0 obviously by neqs consider F such that between A E F from 0 by (II, 2) 1 obviously by neqs so consider G such that between F C G from 0 by (II, 2) 2 obviously by incidence so consider D such that ( a. on line E a on line G a on line D a) (between A D C between F D C) using K (MATCH MP TAC (II, 4)) from 0, 1 obviously (by eqs split) qed from 0, 1, 2 by (II, 1), (II, 3)
26 Ordering along a line THEOREM 4. Of any three points A, B, C on a line there always is one that lies between the other two.
27 Ordering along a line THEOREM 4. Of any three points A, B, C on a line there always is one that lies between the other two. on line A a on line B a on line C a A B A C B C between A B C between B A C between A C B (THEOREM 4)
28 Ordering along a line THEOREM 5. Given any four points on a line, it is always possible to label them A, B, C, D in such a way that the point labelled B lies between A and C and also between A and D, and furthermore, that the point labelled C lies between A and D and also between B and D.
29 Ordering along a line THEOREM 5. Given any four points on a line, it is always possible to label them A, B, C, D in such a way that the point labelled B lies between A and C and also between A and D, and furthermore, that the point labelled C lies between A and D and also between B and D. ( between A B C between B C D between A B D between A C D ( between A B C between A C D between A B D between B C D ) ) (THEOREM 5)
30 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?]
31 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?] Where is B in relation to A and P?
32 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?] Where is B in relation to A and P? If between A and P, then we can reason transitively that Q is between P and Q.
33 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?] Where is B in relation to A and P? If between A and P, then we can reason transitively that Q is between P and Q. We know P cannot be between A and B.
34 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?] Where is B in relation to A and P? If between A and P, then we can reason transitively that Q is between P and Q. We know P cannot be between A and B. If A is between P and B:
35 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?] Where is B in relation to A and P? If between A and P, then we can reason transitively that Q is between P and Q. We know P cannot be between A and B. If A is between P and B: Where is B in relation to A and Q?
36 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?] Where is B in relation to A and P? If between A and P, then we can reason transitively that Q is between P and Q. We know P cannot be between A and B. If A is between P and B: Where is B in relation to A and Q? If between A and Q, we can again reason transitively.
37 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?] Where is B in relation to A and P? If between A and P, then we can reason transitively that Q is between P and Q. We know P cannot be between A and B. If A is between P and B: Where is B in relation to A and Q? If between A and Q, we can again reason transitively. If A is between B and Q, we reason transitively to a contradiction.
38 Too many case splits so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 by... [?] Where is B in relation to A and P? If between A and P, then we can reason transitively that Q is between P and Q. We know P cannot be between A and B. If A is between P and B: Where is B in relation to A and Q? If between A and Q, we can again reason transitively. If A is between B and Q, we reason transitively to a contradiction. If Q is between A and B, we again reason transitively to a contradiction.
39 Reduce to ordering of naturals finite X collinear X f. A. B. C. A X B X C X between A B C (f A < f B f B < f C) (f C < f B f B < f A) A. B. A X B X (A = B f A = f B).
40 Reduce to ordering of naturals finite X collinear X f. A. B. C. A X B X C X between A B C (f A < f B f B < f C) (f C < f B f B < f A) A. B. A X B X (A = B f A = f B). so consider R such that between A R B 7 have between P A Q between P B Q from 6 by... 8 hence between P R Q from 6, 7 using ORDER TAC {P, Q, R, A, B}
41 Jordan Curve Theorem for Polygons THEOREM 9. Every single [simple] polygon lying in a plane α separates the points of the plane α that are not on the polygonal segment of the polygon into two regions, [...]. A B B A
42 Formalisation of Polygonal Segments adjacent : [] [(point, point)] adjacent [P 0, P 1, P 2,..., P n ] = zip (butlast [P 0, P 1, P 2,..., P n ]) (tail [P 0, P 1, P, 2,..., P n ]) = zip [ P 0, P 1, P 2,..., P n 1 ] [ P 1, P 2, P 3,..., P n ] = [(P 0, P 1 ), (P 1, P 2 ), (P 2, P 3 ),..., (P n 1, P n )] on polypath : [point] point bool on polypath Ps P mem P Ps x y. mem (x, y) adjacent Ps between x P y
43 Simple polygons simple polygon : [point] bool def simple polygon Ps 3 length Ps head ps = last Ps pairwise ( ) (butlast Ps) ( P. Q. X. ( mem X Ps mem (P, Q) (adjacent Ps) between P X Q ) pairwise (λ(p, Q) (P, Q ). ( X. between P X P between Q X Q ) (adjacent Ps)).
44 Polygonal Jordan Curve Theorem simple polygon Ps P. Q. on polypath Ps P on polypath Ps Q polypath connected (on polypath Ps) P Q simple polygon Ps on polypath Ps P on polypath Ps Q on polypath Ps R polypath connected (on polypath Ps) P Q polypath connected (on polypath Ps) P R polypath connected (on polypath Ps) Q R
45 Jordan Curve Theorem for Polygons With the aid of Theorem 8, one obtains [the theorem] without much difficulty. Hilbert A B B A
46 Jordan Curve Theorem for Polygons With the aid of Theorem 8, one obtains [the theorem] without much difficulty. Hilbert B A
47 Prose Proofs Almost all useless without more axioms.
48 Prose Proofs Almost all useless without more axioms. Plumb line proof requires that we can cast rays in a fixed direction.
49 Prose Proofs Almost all useless without more axioms. Plumb line proof requires that we can cast rays in a fixed direction. Winding proof assumes a theory of angles.
50 Prose Proofs Almost all useless without more axioms. Plumb line proof requires that we can cast rays in a fixed direction. Winding proof assumes a theory of angles. Both require reasoning about continuity.
51 Veblen to the Rescue? [Jordan s] proof, however, is unsatisfactory to many mathematicians. It assumes the theorem without proof in the important special case of a simple polygon. Veblen
52 Veblen to the Rescue? [Jordan s] proof, however, is unsatisfactory to many mathematicians. It assumes the theorem without proof in the important special case of a simple polygon. Veblen [Veblen s] proof was part of his larger project to axiomatise analysis situs as an isolated field of mathematics. The model for this project was Hilbert s axiomatisation of the foundations of geometry in 1899.
53 Veblen s Proof Suppose Q 1 Q 2 cuts P at O. Then we cannot connect Q 1 and Q 2 by any polygonal path without crossing the polygon. P2 P3 Q2 O Q1 Q7 P4 P5 Q6 P1 Q3 Q4
54 Veblen s Proof Suppose polygon q intersects polygon p n on P 1 P 2 exactly once at O. We must find another point of intersection with another segment of P n. P2 P3 pn Q2 O Q7 Q5 q P4 P5 Q1 Q6 P1 Q3 Q4
55 Veblen s Proof q meets P 1 P 2 P 3 somewhere other than O. P 1 P 3. Suppose it meets on P2 P3 pn Q2 O Q7 Q5 q P4 P5 Q1 Q6 P1 Q3 Q4
56 Veblen s Proof Obtain O k Q 2 Q 3 Q 4 Q 5 Q 6 O j, which has a point inside and also a point outside the triangle P 1 P 2 P 3 and cuts the [triangle] P 1 P 2 P 3 only once. (my emphasis) P2 P3 pn Q2 O Q5 Oj q Ok P4 P5 Q6 P1 Q3 Q4
57 Veblen s Proof Hence it has a point inside and a point outside any triangle of which P 1 P 3 is a side. P2 P3 pn Q2 O Q5 Oj q Ok P4 P5 Q6 P1 Q3 Q4
58 Veblen s Proof From this we conclude that O k Q 2 Q 3 Q 4 Q 5 Q 6 O j cuts either P 3 P 4 or P 1 P 4. P2 P3 pn Q2 O Q5 Oj q Ok P4 P5 Q6 P1 Q3 Q4
59 Veblen s Proof continuing this process P2 P3 pn Q2 O Q5 Oj q Ok P4 P5 Q6 P1 Q3 Q4
60 Veblen s Proof continuing this process? P2 P3 pn Q2 Q6 Q q Ok P4 P5 Oj Q7 Ok P1 Q3 Q4
61 As it turns out... According to Guggenheimer (citing Lennes and Hahn), the proof assumes the polygon can be triangulated and is only valid for convex polygons.
62 As it turns out... According to Guggenheimer (citing Lennes and Hahn), the proof assumes the polygon can be triangulated and is only valid for convex polygons. According to Hahn, the proof is just inconclusive.
63 As it turns out... According to Guggenheimer (citing Lennes and Hahn), the proof assumes the polygon can be triangulated and is only valid for convex polygons. According to Hahn, the proof is just inconclusive.
64 New Proof by Parity B P2 P s P3 O A Qs P4 P5 P7 P6 P1 P8
65 New Proof by Parity B P2 P s P3 A Qs P4 P5 P7 P6 P1 P8
66 New Proof by Parity B P2 P s P3 A Qs P4 P5 P7 P6 P1 P8
67 New Proof by Parity B P2 P s P3 A Qs P4 P5 P7 P6 P1 P8
68 New Proof by Parity B P2 P s P3 A Qs P4 P5 P7 P6 P1 P8
69 New Proof by Parity B P2 P s P3 A Qs P4 P5 P7 P6 P1 Y P8
70 Crossing a Triangle C P 4 P 5 P 1 P 3 P 2 P 7 A P 9 P 8 P 6 B P 10
71 Context (Γ : bool) C P 4 P 5 P 1 P 3 A P 2 P 9 P 8 P 7 P 6 B P 10
72 Definition of Crossings def crossing (A, B, C) Γ P i P i+1 0, if between A P i B between A P i+1 B 1, else if R. between P i R P i+1 between A R B 1, else if between A P i B = ( R. between P i R P i+1 in triangle (A, B, C) R Γ) 0, otherwise. (1)
73 Definition of Context change def Γ next (A, B, C) Γ P i P i+1 in triangle (A, B, C) P i+1 on triangle (A, B, C) P i+1 ( ) ( R. between Pi R P i+1 in triangle (A, B, C) R). on triangle (A, B, C) P i Γ) Γ final (A, B, C) Γ [] = Γ Γ final (A, B, C) Γ ((P i, P i+1 ) : segments) = Γ final (A, B, C) (Γ next (A, B, C) Γ P i P i+1 ) segments
74 Crossings cases C P 2 C C P 1 P 2 A B A B A B P 1 C P 1 P 1 C P 2 C P 1 P 1 A B A B A B P 2 P 2 P 2
75 A Crossings Lemma theorem ( a. on line A a on line B a on line C a) crossing (A, B, C) X P i P i+1 = 1 crossing (A, C, B) X P i P i+1 = 1 crossing (B, C, A) X P i P i+1 = 0 ( a. on line A a on line B a on line C a) on polypath [P i, P i+1 ] A on polypath [P i, P i+1 ] B on polypath [P i, P i+1 ] C ( on triangle (A, B, C) P i (in triangle (A, B, C) P i crossing (A, B, C) Γ P i P i+1 + crossing (A, C, B) Γ P i P i+1 + crossing (B, C, A) Γ P i P i+1 = 1 Γ = Γ next (A, B, C) Γ P i P i+1 Γ))
76 Parity of Crossings polypath crossings (A, B, C) Γ (adjacent Ps) > 0 Q. on polypath Ps Q between A Q B Qs = [P] + Ps + [P] Γ initial = Γ final (A, B, C) Γ (adjacent Qs) on polypath Qs A on polypath Qs B on polypath Qs C ( a. on line A a on line B a on line C a) polypath crossings (A, B, C) Γ initial (adjacent Qs) even + polypath crossings (A, C, B) Γ initial (adjacent Qs) + polypath crossings (B, C, A) Γ initial (adjacent Qs)
77 Moving a vertex (well-definedness) Qs = [P] + Ps + [P] on polypath Qs A on polypath Qs B ( a. on line A a on line B a on line C a) ( a. on line A a on line B a on line C a) Γ. polypath crossings (A, B, C) (Γ final (A, B, C) Γ (adjacent Qs)) (adjacent Qs) = polypath crossings (A, B, C ) (Γ final (A, B, C ) Γ (adjacent Qs)) (adjacent Qs)
78 Verified Theorem If two closed polygonal segments intersect at a point, then they meet again at another point. P2 Q2 P1 Q1
79 Verified Theorem ( a.on line P 1 a on line P 2 a on line Q 1 a on line Q 2 a) between P1 X P2 between Q1 X Q2 Y.on polypath (P2 : Ps)Y on polypath (Q1 : Q2 : Qs) Y on polypath (Q2 : Qs) Y on polypath (P1 : P2 : Ps) Y
80 Polygonal Jordan Curve Theorem: Part 2 There are at most two regions in the plane of a polygon which cannot be connected by a polygonal segment.
81 Polygonal Jordan Curve Theorem: Part 2 There are at most two regions in the plane of a polygon which cannot be connected by a polygonal segment. Consider a path which follows the edges of the polygon, staying close enough so as to avoid intersecting it.
82 Polygonal Jordan Curve Theorem: Part 2 There are at most two regions in the plane of a polygon which cannot be connected by a polygonal segment. Consider a path which follows the edges of the polygon, staying close enough so as to avoid intersecting it. But in our general setting, we cannot run paths parallel to the sides of the polygon.
83 Polygonal Jordan Curve Theorem: Part 2 There are at most two regions in the plane of a polygon which cannot be connected by a polygonal segment. Consider a path which follows the edges of the polygon, staying close enough so as to avoid intersecting it. But in our general setting, we cannot run paths parallel to the sides of the polygon. We cannot measure or compare distances (no ruler or compass)
84 Polygonal Jordan Curve Theorem: Part 2 There are at most two regions in the plane of a polygon which cannot be connected by a polygonal segment. Consider a path which follows the edges of the polygon, staying close enough so as to avoid intersecting it. But in our general setting, we cannot run paths parallel to the sides of the polygon. We cannot measure or compare distances (no ruler or compass) We cannot reason about our orientation via angles.
85 Polygonal Jordan Curve Theorem: Part 2 There are at most two regions in the plane of a polygon which cannot be connected by a polygonal segment. Consider a path which follows the edges of the polygon, staying close enough so as to avoid intersecting it. But in our general setting, we cannot run paths parallel to the sides of the polygon. We cannot measure or compare distances (no ruler or compass) We cannot reason about our orientation via angles. How do we squeeze through corridors in the maze which might be infinitesimally narrow?
86 Polygonal JCT Part 2: Proof P s
87 Polygonal JCT Part 2: Proof X Y P s
88 Polygonal JCT Part 2: Proof X Y P s
89 Lines-of-sight X Y P s Where are we?
90 Lines-of-sight X P10 P11 Y P0 P s P12 Let s see: consider all the points between P 0 and X and P 0 and Y
91 Lines-of-sight X P10 P11 Y P0 P s P12 Now pick out the intersections along the polygon s path.
92 Lines-of-sight X P10 P11 Y P0 P s P12 Use ORDER TAC
93 Lines-of-sight X P10 Z P11 Y P0 P s P12 Raycast Ps X P 0. on polypath Ps X on polypath Ps P 0 Z. on polypath Ps Z (between X Z P 0 P 0 = Z) ( R. between X R Z on polypath Ps R)
94 Lines-of-sight X P10 Z P11 Y P0 P s P12 X has line-of-sight to the point Z on edge P 10 P 11.
95 First Move: Navigating a Local Concavity X P10 Z P11 Y P0 P s P12 We now want to navigate so that X has line-of-sight to the next edge: P 11 P 12.
96 First Move: Navigating a Local Concavity X P10 Z P11 Y P0 P s P12 X and P 12 are on opposite sides of the line P 10 P 11.
97 First Move: Navigating a Local Concavity X P10 Z P11 Y P0 P s P12 X and P 12 are on opposite sides of the line P 10 P 11. Formally, there is a point between X and P 12 on the line P 10 P 11.
98 First Move: Navigating a Local Concavity X P10 Z P11 Y P0 P s P12 X and P 12 are on opposite sides of the line P 10 P 11. Formally, there is a point between X and P 12 on the line P 10 P 11.
99 First Move: Navigating a Local Concavity X P 10 Z P 11 Let s take a closer look. Y P 0 P s P 12
100 First Move: Navigating a Local Concavity X P 10 Z P 11 Z Y Find some Z in the direction P 10 P 11 by Axiom II,2 P 10 P 11 Z. between P 10 P 11 Z P 0 (raycast if necessary). P s P 12
101 First Move: Navigating a Local Concavity X P 10 Z P 11 Z Y X does not have line-of-sight to Z P 0 P s P 12
102 First Move: Navigating a Local Concavity X P 10 Z P 11 Z Y X does not have line-of-sight to Z Let s draw the triangle ZZ X. P 0 P s P 12
103 First Move: Navigating a Local Concavity X P 19 P 10 Z P 11 Z Y Note that the first point which is inside this triangle is P 19. P 0 P s P 12
104 First Move: Navigating a Local Concavity X P 19 P 10 Z P 11 Z Formally, Y 1. there is no point between P 19 and Z on the line XZ; P 0 P s P 12
105 First Move: Navigating a Local Concavity X P 19 P 10 Z P 11 Z Y Formally, 1. there is no point between P 19 and Z on the line XZ; 2. there is no point between P 19 and X on the line ZZ ; P 0 P s P 12
106 First Move: Navigating a Local Concavity X P 19 P 10 Z P 11 Z P 0 Y Formally, 1. there is no point between P 19 and Z on the line XZ; 2. there is no point between P 19 and X on the line ZZ ; 3. there is no point between P 19 and Z on the line XZ ; P s P 12
107 First Move: Navigating a Local Concavity S X P 19 P 10 Z P 11 Z We now want to find the point S where Z P 19 meets XZ. Y P 0 P s P 12
108 First Move: Navigating a Local Concavity S X P 19 P 10 Z P 11 Y a Z We now want to find the point S where Z P 19 meets XZ. Use Pasch s Axiom once. P 0 P s P 12
109 First Move: Navigating a Local Concavity b S X S P 19 P 10 Z P 11 Z We now want to find the point S where Z P 19 meets XZ. Use Pasch s Axiom once. And once more. Y P 0 P s P 12
110 First Move: Navigating a Local Concavity S X P 10 Z P 11 Z Y We now look at the triangle ZZ S P 0 P s P 12
111 First Move: Navigating a Local Concavity S X P 10 Z P 11 Z Y We now look at the triangle ZZ S It doesn t contain any points of the polygon. So any lines between its edges are lines-of-sight. P 0 P s P 12
112 First Move: Navigating a Local Concavity S X P 10 X Z P 11 Z Y We now look at the triangle ZZ S It doesn t contain any points of the polygon. So any lines between its edges are lines-of-sight. So pick a point X between S and Z (Hilbert s Theorem 4). P 0 P s P 12
113 First Move: Navigating a Local Concavity X X P 10 P 11 Z Y P 0 P s P 12
114 First Move: Navigating a Local Concavity X P10 X Z P11 Y P0 P s P12 We still need line-of-sight to a point on P 11 P 12.
115 First Move: Navigating a Local Concavity X X P 10 Z P 11 Z Y P 0 P s P 12
116 First Move: Navigating a Local Concavity X X P 10 Z P 11 Z Y P 15 P 0 P s P 12
117 First Move: Navigating a Local Concavity X X P 10 P 11 Z Y S P 15 P 0 P s P 12
118 First Move: Navigating a Local Concavity X X P 10 P 11 Z Y S P 16 P 15 P 0 P s P 12
119 First Move: Navigating a Local Concavity X X P 10 P 11 Z P 16 Y S P 15 P 0 P s P 12
120 First Move: Navigating a Local Concavity X X P 10 P 11 Z P 16 Y S P 15 P 0 P s P 12
121 First Move: Navigating a Local Concavity X X P 10 P 11 Z Z Y S P 16 P 15 P 0 P s P 12
122 First Move: Navigating a Local Concavity X X P 10 P 11 Z Z Y P 16 P 15 P 0 P s P 12
123 Second Move: Navigating a Local Convexity X P10 X Z P11 Y P0 P s P12 P13 We now want to navigate so that Z has line-of-sight to the next edge: P 12 P 13.
124 Second Move: Navigating a Local Convexity X P10 X Z P11 Y P0 P s P12 P13 We now want to navigate so that Z has line-of-sight to the next edge: P 12 P 13. Formally, Z and P 13 are on the same side of the line P 11 P 12.
125 Second Move: Navigating a Local Convexity X P10 X Z P11 Y P0 P s P12 P13 We now want to navigate so that Z has line-of-sight to the next edge: P 12 P 13. Formally, Z and P 13 are on the same side of the line P 11 P 12. More formally, there is no point between Z and P 13 on the line P 11 P 12.
126 Second Move: Navigating a Local Convexity X P10 X Z P11 Y P15 P0 P s P12 P13 Squeeze! on polypath (Ps [P 11, P 12 ]) P 11 ( X. between Z X P 11 on polypath (Ps [P 11, P 12 ]) X ) ( X. between P 11 X P 12 on polypath (Ps [P 11, P 12 ]) X ) S. between Z S P 11 X. in triangle (S, P 11, P 12 ) X on polypath (Ps [P 11, P 12 ]) X.
127 Second Move: Navigating a Local Convexity X P10 X P11 S Z Y P15 P0 P s P12 P13 Squeeze! on polypath (Ps [P 11, P 12 ]) P 11 ( X. between Z X P 11 on polypath (Ps [P 11, P 12 ]) X ) ( X. between P 11 X P 12 on polypath (Ps [P 11, P 12 ]) X ) S. between Z S P 11 X. in triangle (S, P 11, P 12 ) X on polypath (Ps [P 11, P 12 ]) X.
128 Second Move: Navigating a Local Convexity X P10 X P11 S Z Y P16 P0 P s P12 P13 Squeeze! on polypath (Ps [P 11, P 12 ]) P 11 ( X. between Z X P 11 on polypath (Ps [P 11, P 12 ]) X ) ( X. between P 11 X P 12 on polypath (Ps [P 11, P 12 ]) X ) S. between Z S P 11 X. in triangle (S, P 11, P 12 ) X on polypath (Ps [P 11, P 12 ]) X.
129 Second Move: Navigating a Local Convexity X P10 X P11 S S Z Y P16 P0 P s P12 P13 Squeeze! on polypath (Ps [P 11, P 12 ]) P 11 ( X. between Z X P 11 on polypath (Ps [P 11, P 12 ]) X ) ( X. between P 11 X P 12 on polypath (Ps [P 11, P 12 ]) X ) S. between Z S P 11 X. in triangle (S, P 11, P 12 ) X on polypath (Ps [P 11, P 12 ]) X.
130 Second Move: Navigating a Local Convexity X P10 X Z P11 S Y P0 P s P12 P13 Squeeze! on polypath (Ps [P 11, P 12 ]) P 11 ( X. between Z X P 11 on polypath (Ps [P 11, P 12 ]) X ) ( X. between P 11 X P 12 on polypath (Ps [P 11, P 12 ]) X ) S. between Z S P 11 X. in triangle (S, P 11, P 12 ) X on polypath (Ps [P 11, P 12 ]) X.
131 Second Move: Navigating a Local Convexity X P10 X Z P11 X Y P0 P s P12 P13 Squeeze! on polypath (Ps [P 11, P 12 ]) P 11 ( X. between Z X P 11 on polypath (Ps [P 11, P 12 ]) X ) ( X. between P 11 X P 12 on polypath (Ps [P 11, P 12 ]) X ) S. between Z S P 11 X. in triangle (S, P 11, P 12 ) X on polypath (Ps [P 11, P 12 ]) X.
132 Second Move: Navigating a Local Convexity X P10 X Z P11 Y P15 P0 P s P12 P13 Squeeze! (on polypath (Ps [P 12, P 13 ])P 12 ( X. between P 13 X P 12 on polypath (Ps [P 12, P 13 ]) X ) ( X. between P 12 X P 11 on polypath (Ps [P 12, P 13 ]) X ) Z. between P 13 Z P 12 X. in triangle (Z, P 12, P 11 ) X on polypath (P [P 12, P 13 ]) X.
133 Second Move: Navigating a Local Convexity X P10 X Z P11 Y P15 P0 P s P12 S P13 Squeeze! (on polypath (Ps [P 12, P 13 ])P 12 ( X. between P 13 X P 12 on polypath (Ps [P 12, P 13 ]) X ) ( X. between P 12 X P 11 on polypath (Ps [P 12, P 13 ]) X ) Z. between P 13 Z P 12 X. in triangle (Z, P 12, P 11 ) X on polypath (P [P 12, P 13 ]) X.
134 Second Move: Navigating a Local Convexity X P10 X Z P11 Y P15 P0 P s P12 S S P13 Squeeze! (on polypath (Ps [P 12, P 13 ])P 12 ( X. between P 13 X P 12 on polypath (Ps [P 12, P 13 ]) X ) ( X. between P 12 X P 11 on polypath (Ps [P 12, P 13 ]) X ) Z. between P 13 Z P 12 X. in triangle (Z, P 12, P 11 ) X on polypath (P [P 12, P 13 ]) X.
135 Second Move: Navigating a Local Convexity X P10 X Z P11 Y P0 P s P12 P13 Squeeze! (on polypath (Ps [P 12, P 13 ])P 12 ( X. between P 13 X P 12 on polypath (Ps [P 12, P 13 ]) X ) ( X. between P 12 X P 11 on polypath (Ps [P 12, P 13 ]) X ) Z. between P 13 Z P 12 X. in triangle (Z, P 12, P 11 ) X on polypath (P [P 12, P 13 ]) X.
136 Rinse and Repeat X X P 10 P 11 Z Y P 0 P s P 12 P 13
137 And again B A
138 Edge-to-edge between P 1 X P 2 P 2 P 3 on polypath (P 1 : P 2 : P 3 : Ps) X on polypath (P 3 : Ps) P 2 ( Z. between X Z X on polypath (P 1 : P 2 : P 3 : Ps) Z) ( Z. between P 1 Z P 2 on polypath (P 2 : P 3 : Ps) Z) ( Z. between P 2 Z P 3 on polypath (P 3 : Ps) Z) Y. Y. polypath connected (on polypath (P 1 : P 2 : P 3 : Ps)) X Y between P 2 Y P 3 on polypath (P 1 : P 2 : P 3 : Ps) Y ) Z. between Y Z Y (P 1 : P 2 : P 3 : Ps) Z).
139 Moving to the first edge simple polygon Ps on polypath Ps X mem (P, Q) (adjacent Ps) between P X Q ( Z. between X Z X on polypath Ps Z) Y. Y. polypath connected (on polypath Ps) X Y on polypath Ps Y between (head Ps) Y (head (tail Ps)) Z. between Y Z Y on polypath Ps Z.
140 Polygonal Jordan Curve Theorem simple polygon Ps P. Q. on polypath Ps P on polypath Ps Q polypath connected (on polypath Ps) P Q simple polygon Ps on polypath Ps P on polypath Ps Q on polypath Ps R polypath connected (on polypath Ps) P Q polypath connected (on polypath Ps) P R polypath connected (on polypath Ps) Q R
141 Polygonal Jordan Curve Theorem simple polygon Ps P. Q. on polypath Ps P on polypath Ps Q polypath connected (on polypath Ps) P Q simple polygon Ps on polypath Ps P on polypath Ps Q on polypath Ps R polypath connected (on polypath Ps) P Q polypath connected (on polypath Ps) P R polypath connected (on polypath Ps) Q R No subgoals
142 Polygonal Jordan Curve Theorem simple polygon Ps P. Q. on polypath Ps P on polypath Ps Q polypath connected (on polypath Ps) P Q simple polygon Ps on polypath Ps P on polypath Ps Q on polypath Ps R polypath connected (on polypath Ps) P Q polypath connected (on polypath Ps) P R polypath connected (on polypath Ps) Q R No subgoals(!)
143 Final Notes Axioms here define what is sometimes called Ordered Geometry.
144 Final Notes Axioms here define what is sometimes called Ordered Geometry. It is astonishing that none of the textbooks of elementary axiomatic geometry gives a proof [of the Polygonal Jordan Curve Theorem from Ordered Geometry] Guggenheimer
145 Final Notes Axioms here define what is sometimes called Ordered Geometry. It is astonishing that none of the textbooks of elementary axiomatic geometry gives a proof [of the Polygonal Jordan Curve Theorem from Ordered Geometry] Guggenheimer Now formally verified in a readable style.
146 The Future of Verified Mathematics e.e > 0 (a,b, c) coprime (a, b) coprime (a, c) coprime (b, c) FINITE a + b = c c > ITSET ( ) {p prime p p divides (a b c)}) 1 EXP (1 + e)
147 The Future of Verified Mathematics e.e > 0 (a,b, c) coprime (a, b) coprime (a, c) coprime (b, c) FINITE a + b = c c > ITSET ( ) {p prime p p divides (a b c)}) 1 EXP (1 + e). No subgoals (?)
A Communications Network???
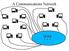 A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points.
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry. l Euclid s five postulates are : ANIL TUTORIALS
 Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry IMporTAnT TErMs, definitions And results l In geometry, we take a point, a line and a plane as undefined terms. l An axiom
Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry IMporTAnT TErMs, definitions And results l In geometry, we take a point, a line and a plane as undefined terms. l An axiom
The statement implies that any three intersection points of two distinct planes lie on a line.
 Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
2.1 Angles, Lines and Parallels & 2.2 Congruent Triangles and Pasch s Axiom
 2 Euclidean Geometry In the previous section we gave a sketch overview of the early parts of Euclid s Elements. While the Elements set the standard for the modern axiomatic approach to mathematics, it
2 Euclidean Geometry In the previous section we gave a sketch overview of the early parts of Euclid s Elements. While the Elements set the standard for the modern axiomatic approach to mathematics, it
MS2013: Euclidean Geometry. Anca Mustata
 MS2013: Euclidean Geometry Anca Mustata January 10, 2012 Warning: please read this text with a pencil at hand, as you will need to draw your own pictures to illustrate some statements. Euclid s Geometry
MS2013: Euclidean Geometry Anca Mustata January 10, 2012 Warning: please read this text with a pencil at hand, as you will need to draw your own pictures to illustrate some statements. Euclid s Geometry
Problem 2.1. Complete the following proof of Euclid III.20, referring to the figure on page 1.
 Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
5. THE ISOPERIMETRIC PROBLEM
 Math 501 - Differential Geometry Herman Gluck March 1, 2012 5. THE ISOPERIMETRIC PROBLEM Theorem. Let C be a simple closed curve in the plane with length L and bounding a region of area A. Then L 2 4 A,
Math 501 - Differential Geometry Herman Gluck March 1, 2012 5. THE ISOPERIMETRIC PROBLEM Theorem. Let C be a simple closed curve in the plane with length L and bounding a region of area A. Then L 2 4 A,
Problem 3.1 (Building up geometry). For an axiomatically built-up geometry, six groups of axioms needed:
 Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Interpretations and Models. Chapter Axiomatic Systems and Incidence Geometry
 Interpretations and Models Chapter 2.1-2.4 - Axiomatic Systems and Incidence Geometry Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas
Interpretations and Models Chapter 2.1-2.4 - Axiomatic Systems and Incidence Geometry Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas
And Now From a New Angle Special Angles and Postulates LEARNING GOALS
 And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
Students are not expected to work formally with properties of dilations until high school.
 Domain: Geometry (G) Cluster: Understand congruence and similarity using physical models, transparencies, or geometry software. Standard: 8.G.1. Verify experimentally the properties of rotations, reflections,
Domain: Geometry (G) Cluster: Understand congruence and similarity using physical models, transparencies, or geometry software. Standard: 8.G.1. Verify experimentally the properties of rotations, reflections,
Geometry Definitions, Postulates, and Theorems. Chapter 3: Parallel and Perpendicular Lines. Section 3.1: Identify Pairs of Lines and Angles.
 Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Finding and Extracting Computational Content in Euclid s Elements
 Finding and Extracting Computational Content in Euclid s Elements Ariel Kellison Septemeber 2017 Outline Introduction Computational Content Intro. Why Implement Results and Future Work Implementing Euclid
Finding and Extracting Computational Content in Euclid s Elements Ariel Kellison Septemeber 2017 Outline Introduction Computational Content Intro. Why Implement Results and Future Work Implementing Euclid
Honors 213. Third Hour Exam. Name
 Honors 213 Third Hour Exam Name Monday, March 27, 2000 100 points Page 1 Please note: Because of multiple exams given Monday, this exam will be returned by Thursday, March 30. 1. (5 pts.) Define what it
Honors 213 Third Hour Exam Name Monday, March 27, 2000 100 points Page 1 Please note: Because of multiple exams given Monday, this exam will be returned by Thursday, March 30. 1. (5 pts.) Define what it
Test 1, Spring 2013 ( Solutions): Provided by Jeff Collins and Anil Patel. 1. Axioms for a finite AFFINE plane of order n.
 Math 532, 736I: Modern Geometry Test 1, Spring 2013 ( Solutions): Provided by Jeff Collins and Anil Patel Part 1: 1. Axioms for a finite AFFINE plane of order n. AA1: There exist at least 4 points, no
Math 532, 736I: Modern Geometry Test 1, Spring 2013 ( Solutions): Provided by Jeff Collins and Anil Patel Part 1: 1. Axioms for a finite AFFINE plane of order n. AA1: There exist at least 4 points, no
(1) Page #1 24 all. (2) Page #7-21 odd, all. (3) Page #8 20 Even, Page 35 # (4) Page #1 8 all #13 23 odd
 Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
The clique number of a random graph in (,1 2) Let ( ) # -subgraphs in = 2 =: ( ) We will be interested in s.t. ( )~1. To gain some intuition note ( )
 The clique number of a random graph in (,1 2) Let () # -subgraphs in = 2 =:() We will be interested in s.t. ()~1. To gain some intuition note ()~ 2 =2 and so ~2log. Now let us work rigorously. () (+1)
The clique number of a random graph in (,1 2) Let () # -subgraphs in = 2 =:() We will be interested in s.t. ()~1. To gain some intuition note ()~ 2 =2 and so ~2log. Now let us work rigorously. () (+1)
The clique number of a random graph in (,1 2) Let ( ) # -subgraphs in = 2 =: ( ) 2 ( ) ( )
 1 The clique number of a random graph in (,1 2) Let () # -subgraphs in = 2 =:() We will be interested in s.t. ()~1. To gain some intuition note ()~ 2 =2 and so ~2log. Now let us work rigorously. () (+1)
1 The clique number of a random graph in (,1 2) Let () # -subgraphs in = 2 =:() We will be interested in s.t. ()~1. To gain some intuition note ()~ 2 =2 and so ~2log. Now let us work rigorously. () (+1)
Solutions to the Test. Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written?
 Solutions to the Test Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written? Answer: The first comprehensive text on geometry is called The Elements
Solutions to the Test Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written? Answer: The first comprehensive text on geometry is called The Elements
Geometry. Parallel Lines.
 1 Geometry Parallel Lines 2015 10 21 www.njctl.org 2 Table of Contents Lines: Intersecting, Parallel & Skew Lines & Transversals Parallel Lines & Proofs Properties of Parallel Lines Constructing Parallel
1 Geometry Parallel Lines 2015 10 21 www.njctl.org 2 Table of Contents Lines: Intersecting, Parallel & Skew Lines & Transversals Parallel Lines & Proofs Properties of Parallel Lines Constructing Parallel
EXTREME POINTS AND AFFINE EQUIVALENCE
 EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
8 Standard Euclidean Triangle Geometry
 8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY
 i MATH 119 A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning earth measure ( ge = earth or land ) + ( metria = measure ). Euclid wrote the Elements
i MATH 119 A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning earth measure ( ge = earth or land ) + ( metria = measure ). Euclid wrote the Elements
Synthetic Geometry. 1.1 Foundations 1.2 The axioms of projective geometry
 Synthetic Geometry 1.1 Foundations 1.2 The axioms of projective geometry Foundations Def: A geometry is a pair G = (Ω, I), where Ω is a set and I a relation on Ω that is symmetric and reflexive, i.e. 1.
Synthetic Geometry 1.1 Foundations 1.2 The axioms of projective geometry Foundations Def: A geometry is a pair G = (Ω, I), where Ω is a set and I a relation on Ω that is symmetric and reflexive, i.e. 1.
Betweenness and the Crossbar Theorem. Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C.
 Betweenness and the Crossbar Theorem Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C. Suppose that both A*B*C and A*C*B. Thus AB+BC =AC, and AC +CB = AB. From this we
Betweenness and the Crossbar Theorem Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C. Suppose that both A*B*C and A*C*B. Thus AB+BC =AC, and AC +CB = AB. From this we
An Approach to Geometry (stolen in part from Moise and Downs: Geometry)
 An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
11 1. Introductory part In order to follow the contents of this book with full understanding, certain prerequisites from high school mathematics will
 11 1. Introductory part In order to follow the contents of this book with full understanding, certain prerequisites from high school mathematics will be necessary. This firstly pertains to the basic concepts
11 1. Introductory part In order to follow the contents of this book with full understanding, certain prerequisites from high school mathematics will be necessary. This firstly pertains to the basic concepts
Hawraa Abbas Almurieb. Axiomatic Systems
 2 Axiomatic Systems 2.1. Introduction to Axiomatic Systems We need undefined terms for any axiomatic system to build the axioms upon them. Which are basic worlds or things for the system. 2.1.1 Definitions
2 Axiomatic Systems 2.1. Introduction to Axiomatic Systems We need undefined terms for any axiomatic system to build the axioms upon them. Which are basic worlds or things for the system. 2.1.1 Definitions
Transformations and Isometries
 Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
MATH 113 Section 8.2: Two-Dimensional Figures
 MATH 113 Section 8.2: Two-Dimensional Figures Prof. Jonathan Duncan Walla Walla University Winter Quarter, 2008 Outline 1 Classifying Two-Dimensional Shapes 2 Polygons Triangles Quadrilaterals 3 Other
MATH 113 Section 8.2: Two-Dimensional Figures Prof. Jonathan Duncan Walla Walla University Winter Quarter, 2008 Outline 1 Classifying Two-Dimensional Shapes 2 Polygons Triangles Quadrilaterals 3 Other
2 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Some Comments on Leaving Certificate Geometry Work in Progress
 Some Comments on Leaving Certificate Geometry Work in Progress D. R. Wilkins April 23, 2016 i Axioms for Leaving Certificate Geometry In 1932, George D. Birkhoff published a paper entitled A set of postulates
Some Comments on Leaving Certificate Geometry Work in Progress D. R. Wilkins April 23, 2016 i Axioms for Leaving Certificate Geometry In 1932, George D. Birkhoff published a paper entitled A set of postulates
Definition (Axiomatic System). An axiomatic system (a set of axioms and their logical consequences) consists of:
 Course Overview Contents 1 AxiomaticSystems.............................. 1 2 Undefined Terms............................... 2 3 Incidence................................... 2 4 Distance....................................
Course Overview Contents 1 AxiomaticSystems.............................. 1 2 Undefined Terms............................... 2 3 Incidence................................... 2 4 Distance....................................
Basic Euclidean Geometry
 hapter 1 asic Euclidean Geometry This chapter is not intended to be a complete survey of basic Euclidean Geometry, but rather a review for those who have previously taken a geometry course For a definitive
hapter 1 asic Euclidean Geometry This chapter is not intended to be a complete survey of basic Euclidean Geometry, but rather a review for those who have previously taken a geometry course For a definitive
Objectives: (What You ll Learn) Identify and model points, lines, planes Identify collinear and coplanar points, intersecting lines and planes
 Geometry Chapter 1 Outline: Points, Lines, Planes, & Angles A. 1-1 Points, Lines, and Planes (What You ll Learn) Identify and model points, lines, planes Identify collinear and coplanar points, intersecting
Geometry Chapter 1 Outline: Points, Lines, Planes, & Angles A. 1-1 Points, Lines, and Planes (What You ll Learn) Identify and model points, lines, planes Identify collinear and coplanar points, intersecting
Definition 2 (Projective plane). A projective plane is a class of points, and a class of lines satisfying the axioms:
 Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Mth 97 Winter 2013 Sections 4.3 and 4.4
 Section 4.3 Problem Solving Using Triangle Congruence Isosceles Triangles Theorem 4.5 In an isosceles triangle, the angles opposite the congruent sides are congruent. A Given: ABC with AB AC Prove: B C
Section 4.3 Problem Solving Using Triangle Congruence Isosceles Triangles Theorem 4.5 In an isosceles triangle, the angles opposite the congruent sides are congruent. A Given: ABC with AB AC Prove: B C
7. The Gauss-Bonnet theorem
 7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
Mathematics As A Liberal Art
 Math 105 Fall 2015 BY: 2015 Ron Buckmire Mathematics As A Liberal Art Class 26: Friday November 13 Fowler 302 MWF 10:40am- 11:35am http://sites.oxy.edu/ron/math/105/15/ Euclid, Geometry and the Platonic
Math 105 Fall 2015 BY: 2015 Ron Buckmire Mathematics As A Liberal Art Class 26: Friday November 13 Fowler 302 MWF 10:40am- 11:35am http://sites.oxy.edu/ron/math/105/15/ Euclid, Geometry and the Platonic
Lattice Polygon s and Pick s Theorem From Dana Paquin and Tom Davis 1 Warm-Up to Ponder
 Lattice Polygon s and Pick s Theorem From Dana Paquin and Tom Davis http://www.geometer.org/mathcircles/pick.pdf 1 Warm-Up to Ponder 1. Is it possible to draw an equilateral triangle on graph paper so
Lattice Polygon s and Pick s Theorem From Dana Paquin and Tom Davis http://www.geometer.org/mathcircles/pick.pdf 1 Warm-Up to Ponder 1. Is it possible to draw an equilateral triangle on graph paper so
EUCLID S GEOMETRY. Raymond Hoobler. January 27, 2008
 EUCLID S GEOMETRY Raymond Hoobler January 27, 2008 Euclid rst codi ed the procedures and results of geometry, and he did such a good job that even today it is hard to improve on his presentation. He lived
EUCLID S GEOMETRY Raymond Hoobler January 27, 2008 Euclid rst codi ed the procedures and results of geometry, and he did such a good job that even today it is hard to improve on his presentation. He lived
Projective geometry and the extended Euclidean plane
 Chapter 2 Projective geometry and the extended Euclidean plane Math 4520, Fall 2017 As we can see from Hilbert s treatment, a completely worked out axiom system for geometry in the plane is quite complicated.
Chapter 2 Projective geometry and the extended Euclidean plane Math 4520, Fall 2017 As we can see from Hilbert s treatment, a completely worked out axiom system for geometry in the plane is quite complicated.
2 Geometry Solutions
 2 Geometry Solutions jacques@ucsd.edu Here is give problems and solutions in increasing order of difficulty. 2.1 Easier problems Problem 1. What is the minimum number of hyperplanar slices to make a d-dimensional
2 Geometry Solutions jacques@ucsd.edu Here is give problems and solutions in increasing order of difficulty. 2.1 Easier problems Problem 1. What is the minimum number of hyperplanar slices to make a d-dimensional
Geometry Reasons for Proofs Chapter 1
 Geometry Reasons for Proofs Chapter 1 Lesson 1.1 Defined Terms: Undefined Terms: Point: Line: Plane: Space: Postulate 1: Postulate : terms that are explained using undefined and/or other defined terms
Geometry Reasons for Proofs Chapter 1 Lesson 1.1 Defined Terms: Undefined Terms: Point: Line: Plane: Space: Postulate 1: Postulate : terms that are explained using undefined and/or other defined terms
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 4 Table of Contents Title Author Square Construction Katherine Bertacini, Rachelle Feldmann, & Kaelyn Koontz Squares and Rectangles Rachelle Feldmann
Transactions in Euclidean Geometry Volume 207F Issue # 4 Table of Contents Title Author Square Construction Katherine Bertacini, Rachelle Feldmann, & Kaelyn Koontz Squares and Rectangles Rachelle Feldmann
Inversive Plane Geometry
 Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
[Me] Meisters, G. H., Polygons have ears, American Mathematical Monthly, June/July 1975, pp
![[Me] Meisters, G. H., Polygons have ears, American Mathematical Monthly, June/July 1975, pp [Me] Meisters, G. H., Polygons have ears, American Mathematical Monthly, June/July 1975, pp](/thumbs/82/87020933.jpg) 4. Applications Meisters [Me] Two-Ears Theorem was motivated by the problem of triangulating a simple polygon. In fact Meisters suggests a greedy, but concise algorithm to achieve this goal, i.e., find
4. Applications Meisters [Me] Two-Ears Theorem was motivated by the problem of triangulating a simple polygon. In fact Meisters suggests a greedy, but concise algorithm to achieve this goal, i.e., find
Answer each of the following problems. Make sure to show your work. Points D, E, and F are collinear because they lie on the same line in the plane.
 Answer each of the following problems. Make sure to show your work. Notation 1. Given the plane DGF in the diagram, which points are collinear? Points D, E, and F are collinear because they lie on the
Answer each of the following problems. Make sure to show your work. Notation 1. Given the plane DGF in the diagram, which points are collinear? Points D, E, and F are collinear because they lie on the
Chapter 1. Essentials of Geometry
 Chapter 1 Essentials of Geometry 1.1 Identify Points, Lines, and Planes Objective: Name and sketch geometric figures so you can use geometry terms in the real world. Essential Question: How do you name
Chapter 1 Essentials of Geometry 1.1 Identify Points, Lines, and Planes Objective: Name and sketch geometric figures so you can use geometry terms in the real world. Essential Question: How do you name
The Cut Locus and the Jordan Curve Theorem
 The Cut Locus and the Jordan Curve Theorem Rich Schwartz November 19, 2015 1 Introduction A Jordan curve is a subset of R 2 which is homeomorphic to the circle, S 1. The famous Jordan Curve Theorem says
The Cut Locus and the Jordan Curve Theorem Rich Schwartz November 19, 2015 1 Introduction A Jordan curve is a subset of R 2 which is homeomorphic to the circle, S 1. The famous Jordan Curve Theorem says
Chapter 2: Properties of Angles and Triangles
 Chapter 2: Properties of Angles and Triangles Section 2.1 Chapter 2: Properties of Angles and Triangles Section 2.1: Angle Properties and Parallel Lines Terminology: Transversal : A line that intersects
Chapter 2: Properties of Angles and Triangles Section 2.1 Chapter 2: Properties of Angles and Triangles Section 2.1: Angle Properties and Parallel Lines Terminology: Transversal : A line that intersects
MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined
 MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined terms used to create definitions. Definitions are used
MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined terms used to create definitions. Definitions are used
MA232A Euclidean and Non-Euclidean Geometry School of Mathematics, Trinity College Michaelmas Term 2017 Some Principles underlying Euclidean Geometry
 MA232A Euclidean and Non-Euclidean Geometry School of Mathematics, Trinity College Michaelmas Term 2017 Some Principles underlying Euclidean Geometry David R. Wilkins 1. Some Principles underlying Euclidean
MA232A Euclidean and Non-Euclidean Geometry School of Mathematics, Trinity College Michaelmas Term 2017 Some Principles underlying Euclidean Geometry David R. Wilkins 1. Some Principles underlying Euclidean
Situation 1: Congruent Triangles vs. Similar Triangles
 Situation 1: Congruent Triangles vs. Similar Triangles Prepared at the University of Georgia EMAT 6500 Date last revised: July 24 th, 2013 Nicolina Scarpelli Prompt: A teacher in a high school Analytic
Situation 1: Congruent Triangles vs. Similar Triangles Prepared at the University of Georgia EMAT 6500 Date last revised: July 24 th, 2013 Nicolina Scarpelli Prompt: A teacher in a high school Analytic
Computational Geometry: Lecture 5
 Computational Geometry: Lecture 5 Don Sheehy January 29, 2010 1 Degeneracy In many of the algorithms that we have discussed so far, we have run into problems when that input is somehow troublesome. For
Computational Geometry: Lecture 5 Don Sheehy January 29, 2010 1 Degeneracy In many of the algorithms that we have discussed so far, we have run into problems when that input is somehow troublesome. For
Chapter 2 Similarity and Congruence
 Chapter 2 Similarity and Congruence Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definition ABC =
Chapter 2 Similarity and Congruence Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definition ABC =
Geometry Mathematics Content Standards
 85 The geometry skills and concepts developed in this discipline are useful to all students. Aside from learning these skills and concepts, students will develop their ability to construct formal, logical
85 The geometry skills and concepts developed in this discipline are useful to all students. Aside from learning these skills and concepts, students will develop their ability to construct formal, logical
2. Draw a non-isosceles triangle. Now make a template of this triangle out of cardstock or cardboard.
 Tessellations The figure at the left shows a tiled floor. Because the floor is entirely covered by the tiles we call this arrangement a tessellation of the plane. A regular tessellation occurs when: The
Tessellations The figure at the left shows a tiled floor. Because the floor is entirely covered by the tiles we call this arrangement a tessellation of the plane. A regular tessellation occurs when: The
Topics in geometry Exam 1 Solutions 7/8/4
 Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
1 Appendix to notes 2, on Hyperbolic geometry:
 1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
GEOMETRY BASIC GEOMETRICAL IDEAS. 3) A point has no dimensions (length, breadth or thickness).
 CLASS 6 - GEOMETRY BASIC GEOMETRICAL IDEAS Geo means Earth and metron means Measurement. POINT 1) The most basic shape in geometry is the Point. 2) A point determines a location. 3) A point has no dimensions
CLASS 6 - GEOMETRY BASIC GEOMETRICAL IDEAS Geo means Earth and metron means Measurement. POINT 1) The most basic shape in geometry is the Point. 2) A point determines a location. 3) A point has no dimensions
Math-2. Lesson 5-3 Two Column Proofs
 Math-2 Lesson 5-3 Two Column Proofs Vocabulary Adjacent Angles have a common side and share a common vertex Vertex. B C D A Common Side A Two-Column Proof is a logical argument written so that the 1st
Math-2 Lesson 5-3 Two Column Proofs Vocabulary Adjacent Angles have a common side and share a common vertex Vertex. B C D A Common Side A Two-Column Proof is a logical argument written so that the 1st
2 Solution of Homework II
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13h2.tex 2 Solution of Homework II 10 Problem 2.1. Prove the Four-point Theorem directly from the Three-point Theorem and the Plane separation Theorem. Answer.
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13h2.tex 2 Solution of Homework II 10 Problem 2.1. Prove the Four-point Theorem directly from the Three-point Theorem and the Plane separation Theorem. Answer.
Angles. An angle is: the union of two rays having a common vertex.
 Angles An angle is: the union of two rays having a common vertex. Angles can be measured in both degrees and radians. A circle of 360 in radian measure is equal to 2π radians. If you draw a circle with
Angles An angle is: the union of two rays having a common vertex. Angles can be measured in both degrees and radians. A circle of 360 in radian measure is equal to 2π radians. If you draw a circle with
Rubber bands. Chapter Rubber band representation
 Chapter 1 Rubber bands In the previous chapter, we already used the idea of looking at the graph geometrically, by placing its nodes on the line and replacing the edges by rubber bands. Since, however,
Chapter 1 Rubber bands In the previous chapter, we already used the idea of looking at the graph geometrically, by placing its nodes on the line and replacing the edges by rubber bands. Since, however,
On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points
 On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points Hu Yuzhong Chen Luping Zhu Hui Ling Xiaofeng (Supervisor) Abstract Consider the following problem. Given n, k N,
On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points Hu Yuzhong Chen Luping Zhu Hui Ling Xiaofeng (Supervisor) Abstract Consider the following problem. Given n, k N,
Section 1.1 Notes. Points - have no size or dimension and named using capital letters A
 Section 1.1 Notes Building Blocks of Geometry Undefined Terms: Points - have no size or dimension and named using capital letters A Lines - have no thickness (1D) and extend forever. Named using 2 points
Section 1.1 Notes Building Blocks of Geometry Undefined Terms: Points - have no size or dimension and named using capital letters A Lines - have no thickness (1D) and extend forever. Named using 2 points
Mathematical Analysis of Tetrahedron (solid angle subtended by any tetrahedron at its vertex)
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter March 29, 2015 Mathematical Analysis of Tetrahedron solid angle subtended by any tetrahedron at its vertex) Harish Chandra Rajpoot Rajpoot,
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter March 29, 2015 Mathematical Analysis of Tetrahedron solid angle subtended by any tetrahedron at its vertex) Harish Chandra Rajpoot Rajpoot,
Thomas Jefferson High School for Science and Technology Program of Studies TJ Math 1
 Course Description: This course is designed for students who have successfully completed the standards for Honors Algebra I. Students will study geometric topics in depth, with a focus on building critical
Course Description: This course is designed for students who have successfully completed the standards for Honors Algebra I. Students will study geometric topics in depth, with a focus on building critical
Which n-venn diagrams can be drawn with convex k-gons?
 Which n-venn diagrams can be drawn with convex k-gons? Jeremy Carroll Frank Ruskey Mark Weston Abstract We establish a new lower bound for the number of sides required for the component curves of simple
Which n-venn diagrams can be drawn with convex k-gons? Jeremy Carroll Frank Ruskey Mark Weston Abstract We establish a new lower bound for the number of sides required for the component curves of simple
Chapter 1-2 Points, Lines, and Planes
 Chapter 1-2 Points, Lines, and Planes Undefined Terms: A point has no size but is often represented by a dot and usually named by a capital letter.. A A line extends in two directions without ending. Lines
Chapter 1-2 Points, Lines, and Planes Undefined Terms: A point has no size but is often represented by a dot and usually named by a capital letter.. A A line extends in two directions without ending. Lines
B. Section 1.1. Chapter 1 Review Booklet A. Vocabulary Match the vocabulary term with its definition. 3. A pair of opposite rays on line p.
 A. Vocabulary Match the vocabulary term with its definition. Point Polygon Angle Sides Postulate Collinear Opposite Rays Vertical angles Coplanar Linear Pair Complementary Vertex Line Adjacent Plane Distance
A. Vocabulary Match the vocabulary term with its definition. Point Polygon Angle Sides Postulate Collinear Opposite Rays Vertical angles Coplanar Linear Pair Complementary Vertex Line Adjacent Plane Distance
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
A Reduction of Conway s Thrackle Conjecture
 A Reduction of Conway s Thrackle Conjecture Wei Li, Karen Daniels, and Konstantin Rybnikov Department of Computer Science and Department of Mathematical Sciences University of Massachusetts, Lowell 01854
A Reduction of Conway s Thrackle Conjecture Wei Li, Karen Daniels, and Konstantin Rybnikov Department of Computer Science and Department of Mathematical Sciences University of Massachusetts, Lowell 01854
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Geometric Constructions
 HISTORY OF MATHEMATICS Spring 2005 Geometric Constructions Notes, activities, assignment; #3 in a series. Note: I m not giving a specific due date for this somewhat vague assignment. The idea is that it
HISTORY OF MATHEMATICS Spring 2005 Geometric Constructions Notes, activities, assignment; #3 in a series. Note: I m not giving a specific due date for this somewhat vague assignment. The idea is that it
Acute Triangulations of Polygons
 Europ. J. Combinatorics (2002) 23, 45 55 doi:10.1006/eujc.2001.0531 Available online at http://www.idealibrary.com on Acute Triangulations of Polygons H. MAEHARA We prove that every n-gon can be triangulated
Europ. J. Combinatorics (2002) 23, 45 55 doi:10.1006/eujc.2001.0531 Available online at http://www.idealibrary.com on Acute Triangulations of Polygons H. MAEHARA We prove that every n-gon can be triangulated
Delaunay Triangulations
 Delaunay Triangulations (slides mostly by Glenn Eguchi) Motivation: Terrains Set of data points A R 2 Height ƒ(p) defined at each point p in A How can we most naturally approximate height of points not
Delaunay Triangulations (slides mostly by Glenn Eguchi) Motivation: Terrains Set of data points A R 2 Height ƒ(p) defined at each point p in A How can we most naturally approximate height of points not
Properties of Angles and Triangles. Outcomes: G1 Derive proofs that involve the properties of angles and triangles.
 Properties of Angles and Triangles Outcomes: G1 Derive proofs that involve the properties of angles and triangles. Achievement Indicators: Generalize, using inductive reasoning, the relationships between
Properties of Angles and Triangles Outcomes: G1 Derive proofs that involve the properties of angles and triangles. Achievement Indicators: Generalize, using inductive reasoning, the relationships between
2-1 Transformations and Rigid Motions. ENGAGE 1 ~ Introducing Transformations REFLECT
 2-1 Transformations and Rigid Motions Essential question: How do you identify transformations that are rigid motions? ENGAGE 1 ~ Introducing Transformations A transformation is a function that changes
2-1 Transformations and Rigid Motions Essential question: How do you identify transformations that are rigid motions? ENGAGE 1 ~ Introducing Transformations A transformation is a function that changes
3 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 25, 2014 All3181\3181_spr14h3.tex Homework has to be turned in this handout. The homework can be done in groups up to three due March 11/12 3 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 25, 2014 All3181\3181_spr14h3.tex Homework has to be turned in this handout. The homework can be done in groups up to three due March 11/12 3 Solution of Homework
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES. V : Introduction to non Euclidean geometry
 FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
LIGHT: Two-slit Interference
 LIGHT: Two-slit Interference Objective: To study interference of light waves and verify the wave nature of light. Apparatus: Two red lasers (wavelength, λ = 633 nm); two orange lasers (λ = 612 nm); two
LIGHT: Two-slit Interference Objective: To study interference of light waves and verify the wave nature of light. Apparatus: Two red lasers (wavelength, λ = 633 nm); two orange lasers (λ = 612 nm); two
1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
 Chapter 1 Line and Angle Relationships 1.1 Sets, Statements and Reasoning Definitions 1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
Chapter 1 Line and Angle Relationships 1.1 Sets, Statements and Reasoning Definitions 1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
2017 SOLUTIONS (PRELIMINARY VERSION)
 SIMON MARAIS MATHEMATICS COMPETITION 07 SOLUTIONS (PRELIMINARY VERSION) This document will be updated to include alternative solutions provided by contestants, after the competition has been mared. Problem
SIMON MARAIS MATHEMATICS COMPETITION 07 SOLUTIONS (PRELIMINARY VERSION) This document will be updated to include alternative solutions provided by contestants, after the competition has been mared. Problem
Elementary Planar Geometry
 Elementary Planar Geometry What is a geometric solid? It is the part of space occupied by a physical object. A geometric solid is separated from the surrounding space by a surface. A part of the surface
Elementary Planar Geometry What is a geometric solid? It is the part of space occupied by a physical object. A geometric solid is separated from the surrounding space by a surface. A part of the surface
Combinatorial Gems. Po-Shen Loh. June 2009
 Combinatorial Gems Po-Shen Loh June 2009 Although this lecture does not contain many offical Olympiad problems, the arguments which are used are all common elements of Olympiad problem solving. Some of
Combinatorial Gems Po-Shen Loh June 2009 Although this lecture does not contain many offical Olympiad problems, the arguments which are used are all common elements of Olympiad problem solving. Some of
HL Maths Junior Certificate Notes by Bronte Smith
 HL Maths Junior Certificate Notes by Bronte Smith Paper 1 Number Systems Applied Arithmetic Sets Algebra Functions Factorising 1. Highest Common Factor ab 2a 2 b + 3ab 2 Find the largest factor that can
HL Maths Junior Certificate Notes by Bronte Smith Paper 1 Number Systems Applied Arithmetic Sets Algebra Functions Factorising 1. Highest Common Factor ab 2a 2 b + 3ab 2 Find the largest factor that can
FOUNDATIONS OF GEOMETRY FOR UNIVERSITY STUDENTS AND HIGH SCHOOL STUDENTS
 arxiv:math/0702029v1 [math.ho] 1 Feb 20 MINISTRY OF GENERAL AND PROFESSIONAL EDUCATION OF RUSSIAN FEDERATION BASHKIR STATE UNIVERSITY SHARIPOV R.A. FOUNDATIONS OF GEOMETRY FOR UNIVERSITY STUDENTS AND HIGH
arxiv:math/0702029v1 [math.ho] 1 Feb 20 MINISTRY OF GENERAL AND PROFESSIONAL EDUCATION OF RUSSIAN FEDERATION BASHKIR STATE UNIVERSITY SHARIPOV R.A. FOUNDATIONS OF GEOMETRY FOR UNIVERSITY STUDENTS AND HIGH
Polygon Triangulation
 Polygon Triangulation Definition Simple Polygons 1. A polygon is the region of a plane bounded by a finite collection of line segments forming a simple closed curve. 2. Simple closed curve means a certain
Polygon Triangulation Definition Simple Polygons 1. A polygon is the region of a plane bounded by a finite collection of line segments forming a simple closed curve. 2. Simple closed curve means a certain
The University of British Columbia Final Examination - December 02, 2014 Mathematics 308. Closed book examination. No calculators.
 The University of British Columbia Final Examination - December 02, 2014 Mathematics 308 Closed book examination. No calculators. Time: 2.5 hours Last Name First Signature Student Number No books, notes,
The University of British Columbia Final Examination - December 02, 2014 Mathematics 308 Closed book examination. No calculators. Time: 2.5 hours Last Name First Signature Student Number No books, notes,
Mth 97 Fall 2013 Chapter 4
 4.1 Reasoning and Proof in Geometry Direct reasoning or reasoning is used to draw a conclusion from a series of statements. Conditional statements, if p, then q, play a central role in deductive reasoning.
4.1 Reasoning and Proof in Geometry Direct reasoning or reasoning is used to draw a conclusion from a series of statements. Conditional statements, if p, then q, play a central role in deductive reasoning.
The angle measure at for example the vertex A is denoted by m A, or m BAC.
 MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana
 University of Groningen Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish
University of Groningen Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish
EM225 Projective Geometry Part 2
 EM225 Projective Geometry Part 2 eview In projective geometry, we regard figures as being the same if they can be made to appear the same as in the diagram below. In projective geometry: a projective point
EM225 Projective Geometry Part 2 eview In projective geometry, we regard figures as being the same if they can be made to appear the same as in the diagram below. In projective geometry: a projective point
<Outline> Mathematical Training Program for Laotian Teachers
 Mathematical Training Program for Laotian Teachers Euclidean Geometry Analytic Geometry Trigonometry Dr Wattana Toutip Department of Mathematics Faculty of Science Khon Kaen University February
Mathematical Training Program for Laotian Teachers Euclidean Geometry Analytic Geometry Trigonometry Dr Wattana Toutip Department of Mathematics Faculty of Science Khon Kaen University February
Math 5320, 3/28/18 Worksheet 26: Ruler and compass constructions. 1. Use your ruler and compass to construct a line perpendicular to the line below:
 Math 5320, 3/28/18 Worksheet 26: Ruler and compass constructions Name: 1. Use your ruler and compass to construct a line perpendicular to the line below: 2. Suppose the following two points are spaced
Math 5320, 3/28/18 Worksheet 26: Ruler and compass constructions Name: 1. Use your ruler and compass to construct a line perpendicular to the line below: 2. Suppose the following two points are spaced
Euclid s Axioms. 1 There is exactly one line that contains any two points.
 11.1 Basic Notions Euclid s Axioms 1 There is exactly one line that contains any two points. Euclid s Axioms 1 There is exactly one line that contains any two points. 2 If two points line in a plane then
11.1 Basic Notions Euclid s Axioms 1 There is exactly one line that contains any two points. Euclid s Axioms 1 There is exactly one line that contains any two points. 2 If two points line in a plane then
Lesson 1: Introduction
 Lesson 1: Introduction Geometry curriculum in primary school How is it?, How is it applied? (LOMCE-Block 4) How should be? Tradition says that at the door of Plato s Acadamy was engraved Let no one ignorant
Lesson 1: Introduction Geometry curriculum in primary school How is it?, How is it applied? (LOMCE-Block 4) How should be? Tradition says that at the door of Plato s Acadamy was engraved Let no one ignorant
