Arithmetic Operations
|
|
|
- Ralph Pierce
- 6 years ago
- Views:
Transcription
1 Arithmetic Operations Arithmetic Operations addition subtraction multiplication division Each of these operations on the integer representations: unsigned two's complement 1
2 Addition One bit of binary addition carry out + a b carry in sum bit 2
3 Addition Truth Table 3 Carry In a b Carry Out Sum Bit
4 Addition Unsigned and 2's complement use the same addition algorithm Due to the fixed precision, throw away the carry out from the msb
5 Two s Complement Addition ( ) ( ) ( ) ( ) ( ) ( ) 5
6 Overflow The condition in which the result of an arithmetic operation cannot fit into the fixed number of bits available. For example: +8 cannot fit into a 3-bit, unsigned representation. It needs 4 bits:
7 Overflow Detection Most architectures have hardware that detects when overflow has occurred (for arithmetic operations). The detection algorithms are simple. 7
8 6-bit examples: Unsigned Overflow Detection Carry out from msbs is overflow in unsigned 8
9 Unsigned Overflow Detection 6-bit examples: No Overflow Overflow! Overflow! 9 Carry out from msbs is overflow in unsigned
10 Two s Complement Overflow Detection When adding 2 numbers of like sign + to + - to and the sign of the result is different! Overflow! Overflow! 10
11 Addition Overflow detection: 2 s complement 6-bit examples ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
12 Subtraction basic algorithm is like decimal 0 0 = = = =? BORROW!
13 Subtraction For two s complement representation The implementation redefines the operation: a b becomes a + (-b) This is a 2-step algorithm: 1. take the two s complement of b (common phrasing for: find the additive inverse of b) 2. do addition 13
14 Subtraction 6-bit, 2 s complement examples ( ) ( ) ( ) ( ) 14
15 Subtraction Overflow detection: 2 s complement If the addition causes overflow, so does the subtraction! ( ) ( ) 15
16 Multiplication 0 0 = = = = 1 Same algorithm as decimal There is a precision problem n bits * n bits n + n bits may be needed 16
17 In HW, space is always designated for a larger precision product. 32 bits * 32 bits 64 bits 17
18 Unsigned Multiplication *
19 Unsigned Multiplication *
20 Two s Complement Slightly trickier: must sign extend the partial products (sometimes!) 20
21 OR Sign extend multiplier and multiplicand to full width of product * product 21 And, use only exact number of lsbs of product
22 Multiplication OK sign ext. partial product reverse or additive inverses find additive inverses OK 22
23 Unsigned Division /3 23
24 Sign Extension The operation that allows the same 2's complement value to be represented, but using more bits (5 bits) _ (8 bits) (4 bits) (8 bits) 24
25 Zero Extension The same type of thing as sign extension, but used to represent the same unsigned value, but using more bits (5 bits) _ (8 bits) (4 bits) (8 bits) 25
26 Truth Table for a Few Logical Operations X Y X and Y X nand Y X or Y X xor Y
27 Logical Operations Logical operations are done bitwise on every computer Invented example: Assume that X,Y, and Z are 8-bit variables and Z, X, Y If X is Y is then Z is 27
28 To selectively clear bit(s) clear a bit means make it a 0 First, make a mask: (the generic description of a set of bits that do whatever you want them to) Within the mask, 1 s for unchanged bits 0 s for cleared bits To clear bits numbered 0,1, and 6 of variable X mask and use the instruction and result, X, mask 28
29 To selectively set bit(s) set a bit means make it a 1 First, make a mask: 0 s for unchanged bits 1 s for set bits To set bits numbered 2,3, and 4 of variable X mask and use the instruction or result, X, mask 29
30 Shift Moving bits around 1) arithmetic shift 2) logical shift 3) rotate Bits can move right or left 30
31 Arithmetic Shift Right sign extension! Left 31
32 Logical Shift Right Left Logical left is the same as arithmetic left. 32
33 Rotate Right Left 33 No bits lost, just moved
34 Assume a set of 4 chars. are in an integersized variable (X). Assume an instruction exists to print out the character all the way to the right putc X (prints D) Invent instructions, and write code to print ABCD, without changing X. 34
35 rotl X, 8 bits putc X # A rotl X, 8 bits putc X # B rotl X, 8 bits putc X # C rotl X, 8 bits putc X # D Karen s solution 35
Arithmetic and Logical Operations
 Arithmetic and Logical Operations 2 CMPE2c x +y + sum Or in tabular form Binary Addition Carry Out Sum B A Carry In Binary Addition And as a full adder a b co ci sum 4-bit Ripple-Carry adder: Carry values
Arithmetic and Logical Operations 2 CMPE2c x +y + sum Or in tabular form Binary Addition Carry Out Sum B A Carry In Binary Addition And as a full adder a b co ci sum 4-bit Ripple-Carry adder: Carry values
BINARY SYSTEM. Binary system is used in digital systems because it is:
 CHAPTER 2 CHAPTER CONTENTS 2.1 Binary System 2.2 Binary Arithmetic Operation 2.3 Signed & Unsigned Numbers 2.4 Arithmetic Operations of Signed Numbers 2.5 Hexadecimal Number System 2.6 Octal Number System
CHAPTER 2 CHAPTER CONTENTS 2.1 Binary System 2.2 Binary Arithmetic Operation 2.3 Signed & Unsigned Numbers 2.4 Arithmetic Operations of Signed Numbers 2.5 Hexadecimal Number System 2.6 Octal Number System
Chapter 4. Operations on Data
 Chapter 4 Operations on Data 1 OBJECTIVES After reading this chapter, the reader should be able to: List the three categories of operations performed on data. Perform unary and binary logic operations
Chapter 4 Operations on Data 1 OBJECTIVES After reading this chapter, the reader should be able to: List the three categories of operations performed on data. Perform unary and binary logic operations
The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop.
 CS 320 Ch 10 Computer Arithmetic The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop. Signed integers are typically represented in sign-magnitude
CS 320 Ch 10 Computer Arithmetic The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop. Signed integers are typically represented in sign-magnitude
Lecture Topics. Announcements. Today: Integer Arithmetic (P&H ) Next: continued. Consulting hours. Introduction to Sim. Milestone #1 (due 1/26)
 Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: continued 1 Announcements Consulting hours Introduction to Sim Milestone #1 (due 1/26) 2 1 Overview: Integer Operations Internal representation
Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: continued 1 Announcements Consulting hours Introduction to Sim Milestone #1 (due 1/26) 2 1 Overview: Integer Operations Internal representation
Chapter 10 Binary Arithmetics
 27..27 Chapter Binary Arithmetics Dr.-Ing. Stefan Werner Table of content Chapter : Switching Algebra Chapter 2: Logical Levels, Timing & Delays Chapter 3: Karnaugh-Veitch-Maps Chapter 4: Combinational
27..27 Chapter Binary Arithmetics Dr.-Ing. Stefan Werner Table of content Chapter : Switching Algebra Chapter 2: Logical Levels, Timing & Delays Chapter 3: Karnaugh-Veitch-Maps Chapter 4: Combinational
Binary Addition. Add the binary numbers and and show the equivalent decimal addition.
 Binary Addition The rules for binary addition are 0 + 0 = 0 Sum = 0, carry = 0 0 + 1 = 0 Sum = 1, carry = 0 1 + 0 = 0 Sum = 1, carry = 0 1 + 1 = 10 Sum = 0, carry = 1 When an input carry = 1 due to a previous
Binary Addition The rules for binary addition are 0 + 0 = 0 Sum = 0, carry = 0 0 + 1 = 0 Sum = 1, carry = 0 1 + 0 = 0 Sum = 1, carry = 0 1 + 1 = 10 Sum = 0, carry = 1 When an input carry = 1 due to a previous
But first, encode deck of cards. Integer Representation. Two possible representations. Two better representations WELLESLEY CS 240 9/8/15
 Integer Representation Representation of integers: unsigned and signed Sign extension Arithmetic and shifting Casting But first, encode deck of cards. cards in suits How do we encode suits, face cards?
Integer Representation Representation of integers: unsigned and signed Sign extension Arithmetic and shifting Casting But first, encode deck of cards. cards in suits How do we encode suits, face cards?
Chapter 4 Arithmetic Functions
 Logic and Computer Design Fundamentals Chapter 4 Arithmetic Functions Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active in View Show mode) Overview Iterative combinational
Logic and Computer Design Fundamentals Chapter 4 Arithmetic Functions Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active in View Show mode) Overview Iterative combinational
CHAPTER V NUMBER SYSTEMS AND ARITHMETIC
 CHAPTER V-1 CHAPTER V CHAPTER V NUMBER SYSTEMS AND ARITHMETIC CHAPTER V-2 NUMBER SYSTEMS RADIX-R REPRESENTATION Decimal number expansion 73625 10 = ( 7 10 4 ) + ( 3 10 3 ) + ( 6 10 2 ) + ( 2 10 1 ) +(
CHAPTER V-1 CHAPTER V CHAPTER V NUMBER SYSTEMS AND ARITHMETIC CHAPTER V-2 NUMBER SYSTEMS RADIX-R REPRESENTATION Decimal number expansion 73625 10 = ( 7 10 4 ) + ( 3 10 3 ) + ( 6 10 2 ) + ( 2 10 1 ) +(
Register Transfer Language and Microoperations (Part 2)
 Register Transfer Language and Microoperations (Part 2) Adapted by Dr. Adel Ammar Computer Organization 1 MICROOPERATIONS Computer system microoperations are of four types: Register transfer microoperations
Register Transfer Language and Microoperations (Part 2) Adapted by Dr. Adel Ammar Computer Organization 1 MICROOPERATIONS Computer system microoperations are of four types: Register transfer microoperations
4 Operations On Data 4.1. Foundations of Computer Science Cengage Learning
 4 Operations On Data 4.1 Foundations of Computer Science Cengage Learning Objectives After studying this chapter, the student should be able to: List the three categories of operations performed on data.
4 Operations On Data 4.1 Foundations of Computer Science Cengage Learning Objectives After studying this chapter, the student should be able to: List the three categories of operations performed on data.
Semester Transition Point. EE 109 Unit 11 Binary Arithmetic. Binary Arithmetic ARITHMETIC
 1 2 Semester Transition Point EE 109 Unit 11 Binary Arithmetic At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
1 2 Semester Transition Point EE 109 Unit 11 Binary Arithmetic At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
2.1. Unit 2. Integer Operations (Arithmetic, Overflow, Bitwise Logic, Shifting)
 2.1 Unit 2 Integer Operations (Arithmetic, Overflow, Bitwise Logic, Shifting) 2.2 Skills & Outcomes You should know and be able to apply the following skills with confidence Perform addition & subtraction
2.1 Unit 2 Integer Operations (Arithmetic, Overflow, Bitwise Logic, Shifting) 2.2 Skills & Outcomes You should know and be able to apply the following skills with confidence Perform addition & subtraction
Chapter 3: part 3 Binary Subtraction
 Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
Basic operators, Arithmetic, Relational, Bitwise, Logical, Assignment, Conditional operators. JAVA Standard Edition
 Basic operators, Arithmetic, Relational, Bitwise, Logical, Assignment, Conditional operators JAVA Standard Edition Java - Basic Operators Java provides a rich set of operators to manipulate variables.
Basic operators, Arithmetic, Relational, Bitwise, Logical, Assignment, Conditional operators JAVA Standard Edition Java - Basic Operators Java provides a rich set of operators to manipulate variables.
COE 202: Digital Logic Design Number Systems Part 2. Dr. Ahmad Almulhem ahmadsm AT kfupm Phone: Office:
 COE 0: Digital Logic Design Number Systems Part Dr. Ahmad Almulhem Email: ahmadsm AT kfupm Phone: 860-7554 Office: -34 Objectives Arithmetic operations: Binary number system Other number systems Base Conversion
COE 0: Digital Logic Design Number Systems Part Dr. Ahmad Almulhem Email: ahmadsm AT kfupm Phone: 860-7554 Office: -34 Objectives Arithmetic operations: Binary number system Other number systems Base Conversion
Integer Representation
 Integer Representation Announcements assign0 due tonight assign1 out tomorrow Labs start this week SCPD Note on ofce hours on Piazza Will get an email tonight about labs Goals for Today Introduction to
Integer Representation Announcements assign0 due tonight assign1 out tomorrow Labs start this week SCPD Note on ofce hours on Piazza Will get an email tonight about labs Goals for Today Introduction to
CS 64 Week 1 Lecture 1. Kyle Dewey
 CS 64 Week 1 Lecture 1 Kyle Dewey Overview Bitwise operation wrap-up Two s complement Addition Subtraction Multiplication (if time) Bitwise Operation Wrap-up Shift Left Move all the bits N positions to
CS 64 Week 1 Lecture 1 Kyle Dewey Overview Bitwise operation wrap-up Two s complement Addition Subtraction Multiplication (if time) Bitwise Operation Wrap-up Shift Left Move all the bits N positions to
4 Operations On Data 4.1. Foundations of Computer Science Cengage Learning
 4 Operations On Data 4.1 Foundations of Computer Science Cengage Learning Objectives After studying this chapter, the student should be able to: List the three categories of operations performed on data.
4 Operations On Data 4.1 Foundations of Computer Science Cengage Learning Objectives After studying this chapter, the student should be able to: List the three categories of operations performed on data.
EE 109 Unit 6 Binary Arithmetic
 EE 109 Unit 6 Binary Arithmetic 1 2 Semester Transition Point At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
EE 109 Unit 6 Binary Arithmetic 1 2 Semester Transition Point At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
Module 2: Computer Arithmetic
 Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
Integers II. CSE 351 Autumn Instructor: Justin Hsia
 Integers II CSE 351 Autumn 2017 Instructor: Justin Hsia Teaching Assistants: Lucas Wotton Michael Zhang Parker DeWilde Ryan Wong Sam Gehman Sam Wolfson Savanna Yee Vinny Palaniappan http://xkcd.com/557/
Integers II CSE 351 Autumn 2017 Instructor: Justin Hsia Teaching Assistants: Lucas Wotton Michael Zhang Parker DeWilde Ryan Wong Sam Gehman Sam Wolfson Savanna Yee Vinny Palaniappan http://xkcd.com/557/
Operations On Data CHAPTER 4. (Solutions to Odd-Numbered Problems) Review Questions
 CHAPTER 4 Operations On Data (Solutions to Odd-Numbered Problems) Review Questions 1. Arithmetic operations interpret bit patterns as numbers. Logical operations interpret each bit as a logical values
CHAPTER 4 Operations On Data (Solutions to Odd-Numbered Problems) Review Questions 1. Arithmetic operations interpret bit patterns as numbers. Logical operations interpret each bit as a logical values
CHW 261: Logic Design
 CHW 261: Logic Design Instructors: Prof. Hala Zayed Dr. Ahmed Shalaby http://www.bu.edu.eg/staff/halazayed14 http://bu.edu.eg/staff/ahmedshalaby14# Slide 1 Slide 2 Slide 3 Digital Fundamentals CHAPTER
CHW 261: Logic Design Instructors: Prof. Hala Zayed Dr. Ahmed Shalaby http://www.bu.edu.eg/staff/halazayed14 http://bu.edu.eg/staff/ahmedshalaby14# Slide 1 Slide 2 Slide 3 Digital Fundamentals CHAPTER
ENE 334 Microprocessors
 Page 1 ENE 334 Microprocessors Lecture 10: MCS-51: Logical and Arithmetic : Dejwoot KHAWPARISUTH http://webstaff.kmutt.ac.th/~dejwoot.kha/ ENE 334 MCS-51 Logical & Arithmetic Page 2 Logical: Objectives
Page 1 ENE 334 Microprocessors Lecture 10: MCS-51: Logical and Arithmetic : Dejwoot KHAWPARISUTH http://webstaff.kmutt.ac.th/~dejwoot.kha/ ENE 334 MCS-51 Logical & Arithmetic Page 2 Logical: Objectives
LAB A Translating Data to Binary
 LAB A Translating Data to Binary Create a directory for this lab and perform in it the following groups of tasks: LabA1.java 1. Write the Java app LabA1 that takes an int via a command-line argument args[0]
LAB A Translating Data to Binary Create a directory for this lab and perform in it the following groups of tasks: LabA1.java 1. Write the Java app LabA1 that takes an int via a command-line argument args[0]
CHAPTER 6 ARITHMETIC, LOGIC INSTRUCTIONS, AND PROGRAMS
 CHAPTER 6 ARITHMETIC, LOGIC INSTRUCTIONS, AND PROGRAMS Addition of Unsigned Numbers The instruction ADD is used to add two operands Destination operand is always in register A Source operand can be a register,
CHAPTER 6 ARITHMETIC, LOGIC INSTRUCTIONS, AND PROGRAMS Addition of Unsigned Numbers The instruction ADD is used to add two operands Destination operand is always in register A Source operand can be a register,
ECEN 468 Advanced Logic Design
 ECEN 468 Advanced Logic Design Lecture 26: Verilog Operators ECEN 468 Lecture 26 Operators Operator Number of Operands Result Arithmetic 2 Binary word Bitwise 2 Binary word Reduction 1 Bit Logical 2 Boolean
ECEN 468 Advanced Logic Design Lecture 26: Verilog Operators ECEN 468 Lecture 26 Operators Operator Number of Operands Result Arithmetic 2 Binary word Bitwise 2 Binary word Reduction 1 Bit Logical 2 Boolean
Chapter 5: Computer Arithmetic. In this chapter you will learn about:
 Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
Beginning C Programming for Engineers
 Beginning Programming for Engineers R. Lindsay Todd Lecture 6: Bit Operations R. Lindsay Todd () Beginning Programming for Engineers Beg 6 1 / 32 Outline Outline 1 Place Value Octal Hexadecimal Binary
Beginning Programming for Engineers R. Lindsay Todd Lecture 6: Bit Operations R. Lindsay Todd () Beginning Programming for Engineers Beg 6 1 / 32 Outline Outline 1 Place Value Octal Hexadecimal Binary
Learning Objectives. Binary over Decimal. In this chapter you will learn about:
 Ref Page Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction
Ref Page Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction
COMP2611: Computer Organization. Data Representation
 COMP2611: Computer Organization Comp2611 Fall 2015 2 1. Binary numbers and 2 s Complement Numbers 3 Bits: are the basis for binary number representation in digital computers What you will learn here: How
COMP2611: Computer Organization Comp2611 Fall 2015 2 1. Binary numbers and 2 s Complement Numbers 3 Bits: are the basis for binary number representation in digital computers What you will learn here: How
Integers II. CSE 351 Autumn Instructor: Justin Hsia
 Integers II CSE 351 Autumn 2016 Instructor: Justin Hsia Teaching Assistants: Chris Ma Hunter Zahn John Kaltenbach Kevin Bi Sachin Mehta Suraj Bhat Thomas Neuman Waylon Huang Xi Liu Yufang Sun http://xkcd.com/571/
Integers II CSE 351 Autumn 2016 Instructor: Justin Hsia Teaching Assistants: Chris Ma Hunter Zahn John Kaltenbach Kevin Bi Sachin Mehta Suraj Bhat Thomas Neuman Waylon Huang Xi Liu Yufang Sun http://xkcd.com/571/
GO - OPERATORS. This tutorial will explain the arithmetic, relational, logical, bitwise, assignment and other operators one by one.
 http://www.tutorialspoint.com/go/go_operators.htm GO - OPERATORS Copyright tutorialspoint.com An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations.
http://www.tutorialspoint.com/go/go_operators.htm GO - OPERATORS Copyright tutorialspoint.com An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations.
Number System. Introduction. Decimal Numbers
 Number System Introduction Number systems provide the basis for all operations in information processing systems. In a number system the information is divided into a group of symbols; for example, 26
Number System Introduction Number systems provide the basis for all operations in information processing systems. In a number system the information is divided into a group of symbols; for example, 26
INF2270 Spring Philipp Häfliger. Lecture 4: Signed Binaries and Arithmetic
 INF2270 Spring 2010 Philipp Häfliger Lecture 4: Signed Binaries and Arithmetic content Karnaugh maps revisited Binary Addition Signed Binary Numbers Binary Subtraction Arithmetic Right-Shift and Bit Number
INF2270 Spring 2010 Philipp Häfliger Lecture 4: Signed Binaries and Arithmetic content Karnaugh maps revisited Binary Addition Signed Binary Numbers Binary Subtraction Arithmetic Right-Shift and Bit Number
Number Systems and Computer Arithmetic
 Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
Number Systems and Conversions UNIT 1 NUMBER SYSTEMS & CONVERSIONS. Number Systems (2/2) Number Systems (1/2) Iris Hui-Ru Jiang Spring 2010
 Contents Number systems and conversion Binary arithmetic Representation of negative numbers Addition of two s complement numbers Addition of one s complement numbers Binary s Readings Unit.~. UNIT NUMBER
Contents Number systems and conversion Binary arithmetic Representation of negative numbers Addition of two s complement numbers Addition of one s complement numbers Binary s Readings Unit.~. UNIT NUMBER
Computer Architecture and Organization: L04: Micro-operations
 Computer Architecture and Organization: L4: Micro-operations By: A. H. Abdul Hafez Abdul.hafez@hku.edu.tr, ah.abdulhafez@gmail.com, hafez@research.iiit.ac.in 1 Outlines 1. Arithmetic microoperation 2.
Computer Architecture and Organization: L4: Micro-operations By: A. H. Abdul Hafez Abdul.hafez@hku.edu.tr, ah.abdulhafez@gmail.com, hafez@research.iiit.ac.in 1 Outlines 1. Arithmetic microoperation 2.
CS 253. January 14, 2017
 CS 253 Department of Computer Science College of Engineering Boise State University January 14, 2017 1/30 Motivation Most programming tasks can be implemented using abstractions (e.g. representing data
CS 253 Department of Computer Science College of Engineering Boise State University January 14, 2017 1/30 Motivation Most programming tasks can be implemented using abstractions (e.g. representing data
Integers II. CSE 351 Autumn 2018
 Integers II CSE 351 Autumn 2018 Instructor: Teaching Assistants: Justin Hsia Akshat Aggarwal An Wang Andrew Hu Brian Dai Britt Henderson James Shin Kevin Bi Kory Watson Riley Germundson Sophie Tian Teagan
Integers II CSE 351 Autumn 2018 Instructor: Teaching Assistants: Justin Hsia Akshat Aggarwal An Wang Andrew Hu Brian Dai Britt Henderson James Shin Kevin Bi Kory Watson Riley Germundson Sophie Tian Teagan
Chapter 3: Arithmetic for Computers
 Chapter 3: Arithmetic for Computers Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point Computer Architecture CS 35101-002 2 The Binary Numbering
Chapter 3: Arithmetic for Computers Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point Computer Architecture CS 35101-002 2 The Binary Numbering
Data Representation. DRAM uses a single capacitor to store and a transistor to select. SRAM typically uses 6 transistors.
 Data Representation Data Representation Goal: Store numbers, characters, sets, database records in the computer. What we got: Circuit that stores 2 voltages, one for logic ( volts) and one for logic (3.3
Data Representation Data Representation Goal: Store numbers, characters, sets, database records in the computer. What we got: Circuit that stores 2 voltages, one for logic ( volts) and one for logic (3.3
Number representations
 Number representations Number bases Three number bases are of interest: Binary, Octal and Hexadecimal. We look briefly at conversions among them and between each of them and decimal. Binary Base-two, or
Number representations Number bases Three number bases are of interest: Binary, Octal and Hexadecimal. We look briefly at conversions among them and between each of them and decimal. Binary Base-two, or
Goals for this Week. CSC 2400: Computer Systems. Bits, Bytes and Data Types. Binary number system. Finite representations of binary integers
 CSC 2400: Computer Systems Bits, Bytes and Data Types 1 Goals for this Week Binary number system Why binary? Converting between decimal and binary and octal and hexadecimal number systems Finite representations
CSC 2400: Computer Systems Bits, Bytes and Data Types 1 Goals for this Week Binary number system Why binary? Converting between decimal and binary and octal and hexadecimal number systems Finite representations
9 Multiplication and Division
 9 Multiplication and Division Multiplication is done by doing shifts and additions. Multiplying two (unsigned) numbers of n bits each results in a product of 2n bits. Example: 0110 x 0011 (6x3) At start,
9 Multiplication and Division Multiplication is done by doing shifts and additions. Multiplying two (unsigned) numbers of n bits each results in a product of 2n bits. Example: 0110 x 0011 (6x3) At start,
CS33 Project Gear Up. Data
 CS33 Project Gear Up Data Project Overview You will be solving a series of puzzles using your knowledge of data representations. IMPORTANT: Collaboration This project has a different collaboration policy
CS33 Project Gear Up Data Project Overview You will be solving a series of puzzles using your knowledge of data representations. IMPORTANT: Collaboration This project has a different collaboration policy
COMP 122/L Lecture 2. Kyle Dewey
 COMP 122/L Lecture 2 Kyle Dewey Outline Operations on binary values AND, OR, XOR, NOT Bit shifting (left, two forms of right) Addition Subtraction Twos complement Bitwise Operations Bitwise AND Similar
COMP 122/L Lecture 2 Kyle Dewey Outline Operations on binary values AND, OR, XOR, NOT Bit shifting (left, two forms of right) Addition Subtraction Twos complement Bitwise Operations Bitwise AND Similar
Digital Arithmetic. Digital Arithmetic: Operations and Circuits Dr. Farahmand
 Digital Arithmetic Digital Arithmetic: Operations and Circuits Dr. Farahmand Binary Arithmetic Digital circuits are frequently used for arithmetic operations Fundamental arithmetic operations on binary
Digital Arithmetic Digital Arithmetic: Operations and Circuits Dr. Farahmand Binary Arithmetic Digital circuits are frequently used for arithmetic operations Fundamental arithmetic operations on binary
Lecture 8: Addition, Multiplication & Division
 Lecture 8: Addition, Multiplication & Division Today s topics: Signed/Unsigned Addition Multiplication Division 1 Signed / Unsigned The hardware recognizes two formats: unsigned (corresponding to the C
Lecture 8: Addition, Multiplication & Division Today s topics: Signed/Unsigned Addition Multiplication Division 1 Signed / Unsigned The hardware recognizes two formats: unsigned (corresponding to the C
Lecture 12 Integers. Computer and Network Security 19th of December Computer Science and Engineering Department
 Lecture 12 Integers Computer and Network Security 19th of December 2016 Computer Science and Engineering Department CSE Dep, ACS, UPB Lecture 12, Integers 1/40 Outline Data Types Representation Conversions
Lecture 12 Integers Computer and Network Security 19th of December 2016 Computer Science and Engineering Department CSE Dep, ACS, UPB Lecture 12, Integers 1/40 Outline Data Types Representation Conversions
Chapter 5: Computer Arithmetic
 Slide 1/29 Learning Objectives Computer Fundamentals: Pradeep K. Sinha & Priti Sinha In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations
Slide 1/29 Learning Objectives Computer Fundamentals: Pradeep K. Sinha & Priti Sinha In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations
COMP 303 Computer Architecture Lecture 6
 COMP 303 Computer Architecture Lecture 6 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 0000 0000 1000 Product 01001000 = 72 n bits x n bits =
COMP 303 Computer Architecture Lecture 6 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 0000 0000 1000 Product 01001000 = 72 n bits x n bits =
Groups of two-state devices are used to represent data in a computer. In general, we say the states are either: high/low, on/off, 1/0,...
 Chapter 9 Computer Arithmetic Reading: Section 9.1 on pp. 290-296 Computer Representation of Data Groups of two-state devices are used to represent data in a computer. In general, we say the states are
Chapter 9 Computer Arithmetic Reading: Section 9.1 on pp. 290-296 Computer Representation of Data Groups of two-state devices are used to represent data in a computer. In general, we say the states are
SIGNED AND UNSIGNED SYSTEMS
 EE 357 Unit 1 Fixed Point Systems and Arithmetic Learning Objectives Understand the size and systems used by the underlying HW when a variable is declared in a SW program Understand and be able to find
EE 357 Unit 1 Fixed Point Systems and Arithmetic Learning Objectives Understand the size and systems used by the underlying HW when a variable is declared in a SW program Understand and be able to find
World Inside a Computer is Binary
 C Programming 1 Representation of int data World Inside a Computer is Binary C Programming 2 Decimal Number System Basic symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Radix-10 positional number system. The radix
C Programming 1 Representation of int data World Inside a Computer is Binary C Programming 2 Decimal Number System Basic symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Radix-10 positional number system. The radix
ECE 2030B 1:00pm Computer Engineering Spring problems, 5 pages Exam Two 10 March 2010
 Instructions: This is a closed book, closed note exam. Calculators are not permitted. If you have a question, raise your hand and I will come to you. Please work the exam in pencil and do not separate
Instructions: This is a closed book, closed note exam. Calculators are not permitted. If you have a question, raise your hand and I will come to you. Please work the exam in pencil and do not separate
Week 7: Assignment Solutions
 Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
CS/COE 0447 Example Problems for Exam 2 Spring 2011
 CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
Bitwise Instructions
 Bitwise Instructions CSE 30: Computer Organization and Systems Programming Dept. of Computer Science and Engineering University of California, San Diego Overview v Bitwise Instructions v Shifts and Rotates
Bitwise Instructions CSE 30: Computer Organization and Systems Programming Dept. of Computer Science and Engineering University of California, San Diego Overview v Bitwise Instructions v Shifts and Rotates
Number Systems CHAPTER Positional Number Systems
 CHAPTER 2 Number Systems Inside computers, information is encoded as patterns of bits because it is easy to construct electronic circuits that exhibit the two alternative states, 0 and 1. The meaning of
CHAPTER 2 Number Systems Inside computers, information is encoded as patterns of bits because it is easy to construct electronic circuits that exhibit the two alternative states, 0 and 1. The meaning of
BITWISE OPERATORS. There are a number of ways to manipulate binary values. Just as you can with
 BITWISE OPERATORS There are a number of ways to manipulate binary values. Just as you can with decimal numbers, you can perform standard mathematical operations - addition, subtraction, multiplication,
BITWISE OPERATORS There are a number of ways to manipulate binary values. Just as you can with decimal numbers, you can perform standard mathematical operations - addition, subtraction, multiplication,
Binary Arithmetic CS 64: Computer Organization and Design Logic Lecture #2 Fall 2018
 Binary Arithmetic CS 64: Computer Organization and Design Logic Lecture #2 Fall 2018 Ziad Matni, Ph.D. Dept. of Computer Science, UCSB Administrative Stuff The class is full I will not be adding more ppl
Binary Arithmetic CS 64: Computer Organization and Design Logic Lecture #2 Fall 2018 Ziad Matni, Ph.D. Dept. of Computer Science, UCSB Administrative Stuff The class is full I will not be adding more ppl
Organisasi Sistem Komputer
 LOGO Organisasi Sistem Komputer OSK 8 Aritmatika Komputer 1 1 PT. Elektronika FT UNY Does the calculations Arithmetic & Logic Unit Everything else in the computer is there to service this unit Handles
LOGO Organisasi Sistem Komputer OSK 8 Aritmatika Komputer 1 1 PT. Elektronika FT UNY Does the calculations Arithmetic & Logic Unit Everything else in the computer is there to service this unit Handles
Kinds Of Data CHAPTER 3 DATA REPRESENTATION. Numbers Are Different! Positional Number Systems. Text. Numbers. Other
 Kinds Of Data CHAPTER 3 DATA REPRESENTATION Numbers Integers Unsigned Signed Reals Fixed-Point Floating-Point Binary-Coded Decimal Text ASCII Characters Strings Other Graphics Images Video Audio Numbers
Kinds Of Data CHAPTER 3 DATA REPRESENTATION Numbers Integers Unsigned Signed Reals Fixed-Point Floating-Point Binary-Coded Decimal Text ASCII Characters Strings Other Graphics Images Video Audio Numbers
CS 31: Intro to Systems Binary Arithmetic. Kevin Webb Swarthmore College January 26, 2016
 CS 31: Intro to Systems Binary Arithmetic Kevin Webb Swarthmore College January 26, 2016 Reading Quiz Unsigned Integers Suppose we had one byte Can represent 2 8 (256) values If unsigned (strictly non-negative):
CS 31: Intro to Systems Binary Arithmetic Kevin Webb Swarthmore College January 26, 2016 Reading Quiz Unsigned Integers Suppose we had one byte Can represent 2 8 (256) values If unsigned (strictly non-negative):
NUMBER SCALING FOR THE LGP-27
 NUMBER SCALING FOR THE LGP-27 5 SCALING The LGP-21 considers all numbers to be within the range -l
NUMBER SCALING FOR THE LGP-27 5 SCALING The LGP-21 considers all numbers to be within the range -l
Bits, Words, and Integers
 Computer Science 52 Bits, Words, and Integers Spring Semester, 2017 In this document, we look at how bits are organized into meaningful data. In particular, we will see the details of how integers are
Computer Science 52 Bits, Words, and Integers Spring Semester, 2017 In this document, we look at how bits are organized into meaningful data. In particular, we will see the details of how integers are
DLD VIDYA SAGAR P. potharajuvidyasagar.wordpress.com. Vignana Bharathi Institute of Technology UNIT 1 DLD P VIDYA SAGAR
 UNIT I Digital Systems: Binary Numbers, Octal, Hexa Decimal and other base numbers, Number base conversions, complements, signed binary numbers, Floating point number representation, binary codes, error
UNIT I Digital Systems: Binary Numbers, Octal, Hexa Decimal and other base numbers, Number base conversions, complements, signed binary numbers, Floating point number representation, binary codes, error
Binary Arithmetic CS 64: Computer Organization and Design Logic Lecture #2
 Binary Arithmetic CS 64: Computer Organization and Design Logic Lecture #2 Ziad Matni Dept. of Computer Science, UCSB Adding this Class The class is full I will not be adding more ppl L Even if others
Binary Arithmetic CS 64: Computer Organization and Design Logic Lecture #2 Ziad Matni Dept. of Computer Science, UCSB Adding this Class The class is full I will not be adding more ppl L Even if others
ECE Digital System Design & Synthesis Exercise 1 - Logic Values, Data Types & Operators - With Answers
 ECE 601 - Digital System Design & Synthesis Exercise 1 - Logic Values, Data Types & Operators - With Answers Fall 2001 Final Version (Important changes from original posted Exercise 1 shown in color) Variables
ECE 601 - Digital System Design & Synthesis Exercise 1 - Logic Values, Data Types & Operators - With Answers Fall 2001 Final Version (Important changes from original posted Exercise 1 shown in color) Variables
Arithmetic and Bitwise Operations on Binary Data
 Arithmetic and Bitwise Operations on Binary Data CSCI 2400: Computer Architecture ECE 3217: Computer Architecture and Organization Instructor: David Ferry Slides adapted from Bryant & O Hallaron s slides
Arithmetic and Bitwise Operations on Binary Data CSCI 2400: Computer Architecture ECE 3217: Computer Architecture and Organization Instructor: David Ferry Slides adapted from Bryant & O Hallaron s slides
Two-Level CLA for 4-bit Adder. Two-Level CLA for 4-bit Adder. Two-Level CLA for 16-bit Adder. A Closer Look at CLA Delay
 Two-Level CLA for 4-bit Adder Individual carry equations C 1 = g 0 +p 0, C 2 = g 1 +p 1 C 1,C 3 = g 2 +p 2 C 2, = g 3 +p 3 C 3 Fully expanded (infinite hardware) CLA equations C 1 = g 0 +p 0 C 2 = g 1
Two-Level CLA for 4-bit Adder Individual carry equations C 1 = g 0 +p 0, C 2 = g 1 +p 1 C 1,C 3 = g 2 +p 2 C 2, = g 3 +p 3 C 3 Fully expanded (infinite hardware) CLA equations C 1 = g 0 +p 0 C 2 = g 1
Integer Encoding and Manipulation
 CSE 2421: Systems I Low-Level Programming and Computer Organization Integer Encoding and Manipulation Presentation D Study: Bryant Chapter 2.1 2.3 Gojko Babić 01-24-2018 Unsigned & Signed Integer Encoding
CSE 2421: Systems I Low-Level Programming and Computer Organization Integer Encoding and Manipulation Presentation D Study: Bryant Chapter 2.1 2.3 Gojko Babić 01-24-2018 Unsigned & Signed Integer Encoding
Number Systems. Both numbers are positive
 Number Systems Range of Numbers and Overflow When arithmetic operation such as Addition, Subtraction, Multiplication and Division are performed on numbers the results generated may exceed the range of
Number Systems Range of Numbers and Overflow When arithmetic operation such as Addition, Subtraction, Multiplication and Division are performed on numbers the results generated may exceed the range of
carry in carry 1101 carry carry
 Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
A complement number system is used to represent positive and negative integers. A complement number system is based on a fixed length representation
 Complement Number Systems A complement number system is used to represent positive and negative integers A complement number system is based on a fixed length representation of numbers Pretend that integers
Complement Number Systems A complement number system is used to represent positive and negative integers A complement number system is based on a fixed length representation of numbers Pretend that integers
CPE300: Digital System Architecture and Design
 CPE300: Digital System Architecture and Design Fall 2011 MW 17:30-18:45 CBC C316 Arithmetic Unit 10122011 http://www.egr.unlv.edu/~b1morris/cpe300/ 2 Outline Recap Fixed Point Arithmetic Addition/Subtraction
CPE300: Digital System Architecture and Design Fall 2011 MW 17:30-18:45 CBC C316 Arithmetic Unit 10122011 http://www.egr.unlv.edu/~b1morris/cpe300/ 2 Outline Recap Fixed Point Arithmetic Addition/Subtraction
Binary Adders. Ripple-Carry Adder
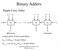 Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
JAVA OPERATORS GENERAL
 JAVA OPERATORS GENERAL Java provides a rich set of operators to manipulate variables. We can divide all the Java operators into the following groups: Arithmetic Operators Relational Operators Bitwise Operators
JAVA OPERATORS GENERAL Java provides a rich set of operators to manipulate variables. We can divide all the Java operators into the following groups: Arithmetic Operators Relational Operators Bitwise Operators
UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT
 UNIT-III 1 KNREDDY UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT Register Transfer: Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Micro operations Logic
UNIT-III 1 KNREDDY UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT Register Transfer: Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Micro operations Logic
Lecture Topics. Announcements. Today: Integer Arithmetic (P&H ) Next: The MIPS ISA (P&H ) Consulting hours. Milestone #1 (due 1/26)
 Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: The MIPS ISA (P&H 2.1-2.14) 1 Announcements Consulting hours Milestone #1 (due 1/26) Milestone #2 (due 2/2) 2 1 Review: Integer Operations Internal
Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: The MIPS ISA (P&H 2.1-2.14) 1 Announcements Consulting hours Milestone #1 (due 1/26) Milestone #2 (due 2/2) 2 1 Review: Integer Operations Internal
1010 2?= ?= CS 64 Lecture 2 Data Representation. Decimal Numbers: Base 10. Reading: FLD Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
 CS 64 Lecture 2 Data Representation Reading: FLD 1.2-1.4 Decimal Numbers: Base 10 Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Example: 3271 = (3x10 3 ) + (2x10 2 ) + (7x10 1 ) + (1x10 0 ) 1010 10?= 1010 2?= 1
CS 64 Lecture 2 Data Representation Reading: FLD 1.2-1.4 Decimal Numbers: Base 10 Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Example: 3271 = (3x10 3 ) + (2x10 2 ) + (7x10 1 ) + (1x10 0 ) 1010 10?= 1010 2?= 1
CS 31: Introduction to Computer Systems. 03: Binary Arithmetic January 29
 CS 31: Introduction to Computer Systems 03: Binary Arithmetic January 29 WiCS! Swarthmore Women in Computer Science Slide 2 Today Binary Arithmetic Unsigned addition Subtraction Representation Signed magnitude
CS 31: Introduction to Computer Systems 03: Binary Arithmetic January 29 WiCS! Swarthmore Women in Computer Science Slide 2 Today Binary Arithmetic Unsigned addition Subtraction Representation Signed magnitude
CS/COE0447: Computer Organization
 CS/COE0447: Computer Organization and Assembly Language Chapter 3 Sangyeun Cho Dept. of Computer Science Five classic components I am like a control tower I am like a pack of file folders I am like a conveyor
CS/COE0447: Computer Organization and Assembly Language Chapter 3 Sangyeun Cho Dept. of Computer Science Five classic components I am like a control tower I am like a pack of file folders I am like a conveyor
CS/COE0447: Computer Organization
 Five classic components CS/COE0447: Computer Organization and Assembly Language I am like a control tower I am like a pack of file folders Chapter 3 I am like a conveyor belt + service stations I exchange
Five classic components CS/COE0447: Computer Organization and Assembly Language I am like a control tower I am like a pack of file folders Chapter 3 I am like a conveyor belt + service stations I exchange
ECE 30 Introduction to Computer Engineering
 ECE 30 Introduction to Computer Engineering Study Problems, Set #6 Spring 2015 1. With x = 1111 1111 1111 1111 1011 0011 0101 0011 2 and y = 0000 0000 0000 0000 0000 0010 1101 0111 2 representing two s
ECE 30 Introduction to Computer Engineering Study Problems, Set #6 Spring 2015 1. With x = 1111 1111 1111 1111 1011 0011 0101 0011 2 and y = 0000 0000 0000 0000 0000 0010 1101 0111 2 representing two s
Binary Adders: Half Adders and Full Adders
 Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
ECE 375: Computer Organization and Assembly Language Programming
 ECE 375: Computer Organization and Assembly Language Programming SECTION OVERVIEW Lab 5 Large Number Arithmetic Complete the following objectives: ˆ Understand and use arithmetic/alu instructions. ˆ Manipulate
ECE 375: Computer Organization and Assembly Language Programming SECTION OVERVIEW Lab 5 Large Number Arithmetic Complete the following objectives: ˆ Understand and use arithmetic/alu instructions. ˆ Manipulate
EEM336 Microprocessors I. Arithmetic and Logic Instructions
 EEM336 Microprocessors I Arithmetic and Logic Instructions Introduction We examine the arithmetic and logic instructions. The arithmetic instructions include addition, subtraction, multiplication, division,
EEM336 Microprocessors I Arithmetic and Logic Instructions Introduction We examine the arithmetic and logic instructions. The arithmetic instructions include addition, subtraction, multiplication, division,
Introduction. Following are the types of operators: Unary requires a single operand Binary requires two operands Ternary requires three operands
 Introduction Operators are the symbols which operates on value or a variable. It tells the compiler to perform certain mathematical or logical manipulations. Can be of following categories: Unary requires
Introduction Operators are the symbols which operates on value or a variable. It tells the compiler to perform certain mathematical or logical manipulations. Can be of following categories: Unary requires
Combinational and sequential circuits (learned in Chapters 1 and 2) can be used to create simple digital systems.
 REGISTER TRANSFER AND MICROOPERATIONS Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Microoperations Logic Microoperations Shift Microoperations Arithmetic Logic Shift
REGISTER TRANSFER AND MICROOPERATIONS Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Microoperations Logic Microoperations Shift Microoperations Arithmetic Logic Shift
MC1601 Computer Organization
 MC1601 Computer Organization Unit 1 : Digital Fundamentals Lesson1 : Number Systems and Conversions (KSB) (MCA) (2009-12/ODD) (2009-10/1 A&B) Coverage - Lesson1 Shows how various data types found in digital
MC1601 Computer Organization Unit 1 : Digital Fundamentals Lesson1 : Number Systems and Conversions (KSB) (MCA) (2009-12/ODD) (2009-10/1 A&B) Coverage - Lesson1 Shows how various data types found in digital
Data Representation COE 301. Computer Organization Prof. Muhamed Mudawar
 Data Representation COE 30 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals Presentation Outline Positional Number
Data Representation COE 30 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals Presentation Outline Positional Number
Addition and multiplication
 Addition and multiplication Arithmetic is the most basic thing you can do with a computer, but it s not as easy as you might expect! These next few lectures focus on addition, subtraction, multiplication
Addition and multiplication Arithmetic is the most basic thing you can do with a computer, but it s not as easy as you might expect! These next few lectures focus on addition, subtraction, multiplication
Floating-Point Data Representation and Manipulation 198:231 Introduction to Computer Organization Lecture 3
 Floating-Point Data Representation and Manipulation 198:231 Introduction to Computer Organization Instructor: Nicole Hynes nicole.hynes@rutgers.edu 1 Fixed Point Numbers Fixed point number: integer part
Floating-Point Data Representation and Manipulation 198:231 Introduction to Computer Organization Instructor: Nicole Hynes nicole.hynes@rutgers.edu 1 Fixed Point Numbers Fixed point number: integer part
Arithmetic and Bitwise Operations on Binary Data
 Arithmetic and Bitwise Operations on Binary Data CSCI 224 / ECE 317: Computer Architecture Instructor: Prof. Jason Fritts Slides adapted from Bryant & O Hallaron s slides 1 Boolean Algebra Developed by
Arithmetic and Bitwise Operations on Binary Data CSCI 224 / ECE 317: Computer Architecture Instructor: Prof. Jason Fritts Slides adapted from Bryant & O Hallaron s slides 1 Boolean Algebra Developed by
CHAPTER 4: Register Transfer Language and Microoperations
 CS 224: Computer Organization S.KHABET CHAPTER 4: Register Transfer Language and Microoperations Outline Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Microoperations
CS 224: Computer Organization S.KHABET CHAPTER 4: Register Transfer Language and Microoperations Outline Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Microoperations
EE260: Logic Design, Spring n Integer multiplication. n Booth s algorithm. n Integer division. n Restoring, non-restoring
 EE 260: Introduction to Digital Design Arithmetic II Yao Zheng Department of Electrical Engineering University of Hawaiʻi at Mānoa Overview n Integer multiplication n Booth s algorithm n Integer division
EE 260: Introduction to Digital Design Arithmetic II Yao Zheng Department of Electrical Engineering University of Hawaiʻi at Mānoa Overview n Integer multiplication n Booth s algorithm n Integer division
