COMP 303 Computer Architecture Lecture 6
|
|
|
- Harvey Cunningham
- 6 years ago
- Views:
Transcription
1 COMP 303 Computer Architecture Lecture 6
2 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = Product = 72 n bits x n bits = 2n bit product Binary makes it easy: 0 => place 0 ( 0 x multiplicand) 1 => place a copy ( 1 x multiplicand) 4 versions of multiply hardware & algorithm: successive refinement
3 Unsigned shift-add multiplier (version 1) 64-bit Multiplicand reg, 64-bit ALU, 64-bit Product reg, 32-bit multiplier reg Multiplicand 64 bits Shift Left 64-bit ALU Multiplier 32 bits Shift Right Product 64 bits Write Control Multiplier = datapath + control
4 Multiply Algorithm Version 1 Start Multiplier0 = 1 1. Test Multiplier0 Multiplier0 = 0 1a. Add multiplicand to product & place the result in Product register Product Multiplier Multiplicand Shift the Multiplicand register left 1 bit. 3. Shift the Multiplier register right 1 bit. n th repetition? No: < n repetitions Yes: n repetitions Done
5 Observations on Multiply Version 1 1/2 bits in multiplicand always 0 => 64-bit adder is wasted 0 s inserted into the least significant bit of multiplicand as shifted => least significant bits of product never changed once formed Instead of shifting multiplicand to left, shift product to right.
6 MULTIPLY HARDWARE Version 2 32-bit Multiplicand reg, 32 -bit ALU, 64-bit Product reg, 32-bit Multiplier reg Multiplicand 32-bit ALU 32 bits Multiplier 32 bits Shift Right Product 64 bits Shift Right Write Control
7 Multiply Algorithm Version 2 Multiplier0 = 1 Start 1. Test Multiplier0 Multiplier0 = 0 1a. Add multiplicand to the left half of product & place the result in the left half of Product register Product Multiplier Multiplicand : : : : : : : : : : : : Shift the Product register right 1 bit. 3. Shift the Multiplier register right 1 bit. n th repetition? No: < n repetitions Yes: n repetitions Done
8 Still more wasted space! Multiplier0 = 1 Start 1. Test Multiplier0 Multiplier0 = 0 1a. Add multiplicand to the left half of product & place the result in the left half of Product register Product Multiplier Multiplicand : : : : : : : : : : : : Shift the Product register right 1 bit. 3. Shift the Multiplier register right 1 bit. n th repetition? No: < n repetitions Yes: n repetitions Done
9 Observations on Multiply Version 2 Product register wastes space that exactly matches size of multiplier Both Multiplier register and Product register require right shift Combine Multiplier register and Product register
10 MULTIPLY HARDWARE Version 3 32-bit Multiplicand reg, 32 -bit ALU, 64-bit Product reg, (0-bit Multiplier reg) Multiplicand 32 bits 32-bit ALU Product (Multiplier) 64 bits Shift Right Write Control
11 Multiply Algorithm Version 3 Multiplicand Multiplier Product0 = 1 Start 1. Test Product0 Product0 = 0 1a. Add multiplicand to the left half of product & place the result in the left half of Product register Product Multiplicand : : : : : : : : Shift the Product register right 1 bit. 32nd repetition? No: < 32 repetitions Yes: 32 repetitions Done
12 Observations on Multiply Version 3 2 steps per bit because Multiplier & Product combined MIPS registers Hi and Lo are left and right half of Product Gives us MIPS instruction MultU What about signed multiplication? easiest solution is to make both positive & remember whether to complement product when done (leave out the sign bit, run for 31 steps) Multiply algorithm 3 will work for signed numbers if partial products are sign-extended as shifted Booth s Algorithm is elegant way to multiply signed numbers using same hardware as before and save cycles can be modified to handle multiple bits at a time
13 Faster Multiplication Whether the multiplicant is to be added or not is known at the beginning of the operation Provide a 32-bit adder for each bit of the multiplier One input is the multiplicand ANDed with a multiplier bit and the other is the output of a prior adder. Speed: just the oerhead of a clock for each bit of the product. log2(32)
14 Shifters Two kinds: logical-- value shifted in is always "0" "0" msb lsb "0" arithmetic-- on right shifts, sign extend msb lsb "0" Note: these are single bit shifts. A given instruction might request 0 to 32 bits to be shifted!
15 Combinational Shifter from MUXes Basic Building Block A B sel to-1 Mux 8-bit right shifter D A 7 A 6 A 5 A 4 A 3 A 2 A 1 A 0 S 2 S 1 S R 7 R 6 R 5 R 4 R 3 R 2 R 1 R 0 What comes in the MSBs? How many levels for 32-bit shifter?
16 Unsigned Divide: Paper & Pencil 1001 Quotient Divisor Dividend Remainder (or Modulo result) See how big a number can be subtracted, creating quotient bit on each step Binary => 1 * divisor or 0 * divisor Dividend = Quotient x Divisor + Remainder 3 versions of divide, successive refinement
17 DIVIDE HARDWARE Version 1 64-bit Divisor reg, 64-bit ALU, 64-bit Remainder reg, 32-bit Quotient reg Divisor 64 bits Shift Right 64-bit ALU Quotient 32 bits Shift Left Remainder 64 bits Write Control
18 Divide Algorithm Version 1 Takes n+1 steps for n-bit Quotient & Rem. Remainder Quotient Divisor Start: Place Dividend in Remainder 1. Subtract the Divisor register from the Remainder register, and place the result in the Remainder register. Remainder 0 Test Remainder Remainder < 0 2a. Shift the Quotient register to the left setting the new rightmost bit to 1. 2b. Restore the original value by adding the Divisor register to the Remainder register, & place the sum in the Remainder register. Also shift the Quotient register to the left, setting the new least significant bit to Shift the Divisor register right 1 bit. n+1 repetition? Done No: < n+1 repetitions Yes: n+1 repetitions (n = 4 here)
19 Observations on Divide Version 1 1/2 bits in divisor always 0 => 1/2 of 64-bit adder is wasted => 1/2 of divisor is wasted Instead of shifting divisor to right, shift remainder to left? 1st step cannot produce a 1 in quotient bit (otherwise too big) => switch order to shift first and then subtract, can save 1 iteration
20 Divide: Paper & Pencil Quotient Divisor Dividend Remainder (or Modulo result) Notice that there is no way to get a 1 in leading digit! (this would be an overflow, since quotient would have n+1 bits)
21 DIVIDE HARDWARE Version 2 32-bit Divisor reg, 32-bit ALU, 64-bit Remainder reg, 32-bit Quotient reg Divisor 32-bit ALU 32 bits Quotient 32 bits Shift Left Remainder 64 bits Shift Left Write Control
22 Divide Algorithm Version 2 Start: Place Dividend in Remainder Remainder Quotient Divisor Shift the Remainder register left 1 bit. 2. Subtract the Divisor register from the left half of the Remainder register, & place the result in the left half of the Remainder register. Remainder 0 Test Remainder Remainder < 0 3a. Shift the Quotient register to the left setting the new rightmost bit to 1. 3b. Restore the original value by adding the Divisor register to the left half of the Remainder register, & place the sum in the left half of the Remainder register. Also shift the Quotient register to the left, setting the new least significant bit to 0. nth repetition? No: < n repetitions Yes: n repetitions (n = 4 here) Done
23 Observations on Divide Version 2 Eliminate Quotient register by combining with Remainder as shifted left Start by shifting the Remainder left as before. Thereafter loop contains only two steps because the shifting of the Remainder register shifts both the remainder in the left half and the quotient in the right half The consequence of combining the two registers together and the new order of the operations in the loop is that the remainder will shifted left one time too many. Thus the final correction step must shift back only the remainder in the left half of the register
24 DIVIDE HARDWARE Version 3 32-bit Divisor reg, 32 -bit ALU, 64-bit Remainder reg, (0-bit Quotient reg) Divisor 32 bits 32-bit ALU HI LO Remainder (Quotient) 64 bits Shift Right Shift Left Write Control
25 Divide Algorithm Version 3 Start: Place Dividend in Remainder Remainder Divisor Shift the Remainder register left 1 bit. 2. Subtract the Divisor register from the left half of the Remainder register, & place the result in the left half of the Remainder register. Remainder 0 Test Remainder Remainder < 0 3a. Shift the Remainder register to the left setting the new rightmost bit to 1. 3b. Restore the original value by adding the Divisor register to the left half of the Remainder register, & place the sum in the left half of the Remainder register. Also shift the Remainder register to the left, setting the new least significant bit to 0. nth repetition? No: < n repetitions Yes: n repetitions (n = 4 here) Done. Shift left half of Remainder right 1 bit.
26 Observations on Divide Version 3 Same Hardware as Multiply: just need ALU to add or subtract, and 64-bit register to shift left or shift right Hi and Lo registers in MIPS combine to act as 64-bit register for multiply and divide Signed Divides: Simplest is to remember signs, make positive, and complement quotient and remainder if necessary Note: Dividend and Remainder must have same sign Note: Quotient negated if Divisor sign & Dividend sign disagree e.g., 7 2 = 3, remainder = 1
361 div.1. Computer Architecture EECS 361 Lecture 7: ALU Design : Division
 361 div.1 Computer Architecture EECS 361 Lecture 7: ALU Design : Division Outline of Today s Lecture Introduction to Today s Lecture Divide Questions and Administrative Matters Introduction to Single cycle
361 div.1 Computer Architecture EECS 361 Lecture 7: ALU Design : Division Outline of Today s Lecture Introduction to Today s Lecture Divide Questions and Administrative Matters Introduction to Single cycle
EECS150 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3
 EECS15 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3 October 8, 22 John Wawrzynek Fall 22 EECS15 - Lec13-cla3 Page 1 Multiplication a 3 a 2 a 1 a Multiplicand b 3 b 2 b
EECS15 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3 October 8, 22 John Wawrzynek Fall 22 EECS15 - Lec13-cla3 Page 1 Multiplication a 3 a 2 a 1 a Multiplicand b 3 b 2 b
Review of Last lecture. Review ALU Design. Designing a Multiplier Shifter Design Review. Booth s algorithm. Today s Outline
 Today s Outline San Jose State University EE176-SJSU Computer Architecture and Organization Lecture 5 HDL, ALU, Shifter, Booth Algorithm Multiplier & Divider Instructor: Christopher H. Pham Review of Last
Today s Outline San Jose State University EE176-SJSU Computer Architecture and Organization Lecture 5 HDL, ALU, Shifter, Booth Algorithm Multiplier & Divider Instructor: Christopher H. Pham Review of Last
EEC 483 Computer Organization
 EEC 483 Computer Organization Chapter 3. Arithmetic for Computers Chansu Yu Table of Contents Ch.1 Introduction Ch. 2 Instruction: Machine Language Ch. 3-4 CPU Implementation Ch. 5 Cache and VM Ch. 6-7
EEC 483 Computer Organization Chapter 3. Arithmetic for Computers Chansu Yu Table of Contents Ch.1 Introduction Ch. 2 Instruction: Machine Language Ch. 3-4 CPU Implementation Ch. 5 Cache and VM Ch. 6-7
Homework 3. Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) CSCI 402: Computer Architectures
 Homework 3 Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) 1 CSCI 402: Computer Architectures Arithmetic for Computers (2) Fengguang Song Department
Homework 3 Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) 1 CSCI 402: Computer Architectures Arithmetic for Computers (2) Fengguang Song Department
Divide: Paper & Pencil
 Divide: Paper & Pencil 1001 Quotient Divisor 1000 1001010 Dividend -1000 10 101 1010 1000 10 Remainder See how big a number can be subtracted, creating quotient bit on each step Binary => 1 * divisor or
Divide: Paper & Pencil 1001 Quotient Divisor 1000 1001010 Dividend -1000 10 101 1010 1000 10 Remainder See how big a number can be subtracted, creating quotient bit on each step Binary => 1 * divisor or
Number Systems and Computer Arithmetic
 Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
Outline. EEL-4713 Computer Architecture Multipliers and shifters. Deriving requirements of ALU. MIPS arithmetic instructions
 Outline EEL-4713 Computer Architecture Multipliers and shifters Multiplication and shift registers Chapter 3, section 3.4 Next lecture Division, floating-point 3.5 3.6 EEL-4713 Ann Gordon-Ross.1 EEL-4713
Outline EEL-4713 Computer Architecture Multipliers and shifters Multiplication and shift registers Chapter 3, section 3.4 Next lecture Division, floating-point 3.5 3.6 EEL-4713 Ann Gordon-Ross.1 EEL-4713
Tailoring the 32-Bit ALU to MIPS
 Tailoring the 32-Bit ALU to MIPS MIPS ALU extensions Overflow detection: Carry into MSB XOR Carry out of MSB Branch instructions Shift instructions Slt instruction Immediate instructions ALU performance
Tailoring the 32-Bit ALU to MIPS MIPS ALU extensions Overflow detection: Carry into MSB XOR Carry out of MSB Branch instructions Shift instructions Slt instruction Immediate instructions ALU performance
MIPS Integer ALU Requirements
 MIPS Integer ALU Requirements Add, AddU, Sub, SubU, AddI, AddIU: 2 s complement adder/sub with overflow detection. And, Or, Andi, Ori, Xor, Xori, Nor: Logical AND, logical OR, XOR, nor. SLTI, SLTIU (set
MIPS Integer ALU Requirements Add, AddU, Sub, SubU, AddI, AddIU: 2 s complement adder/sub with overflow detection. And, Or, Andi, Ori, Xor, Xori, Nor: Logical AND, logical OR, XOR, nor. SLTI, SLTIU (set
Today s Outline. CS152 Computer Architecture and Engineering Lecture 5. VHDL, Multiply, Shift
 Today s Outline CS152 Computer Architecture and Engineering Lecture 5 VHDL, Multiply, Shift Feb 8, 1999 John Kubiatowicz (http.cs.berkeley.edu/~kubitron) Review of Last lecture Intro to VHDL Administrative
Today s Outline CS152 Computer Architecture and Engineering Lecture 5 VHDL, Multiply, Shift Feb 8, 1999 John Kubiatowicz (http.cs.berkeley.edu/~kubitron) Review of Last lecture Intro to VHDL Administrative
CPS 104 Computer Organization and Programming
 CPS 104 Computer Organization and Programming Lecture 9: Integer Arithmetic. Robert Wagner CPS104 IMD.1 RW Fall 2000 Overview of Today s Lecture: Integer Multiplication and Division. Read Appendix B CPS104
CPS 104 Computer Organization and Programming Lecture 9: Integer Arithmetic. Robert Wagner CPS104 IMD.1 RW Fall 2000 Overview of Today s Lecture: Integer Multiplication and Division. Read Appendix B CPS104
Review from last time. CS152 Computer Architecture and Engineering Lecture 6. Verilog (finish) Multiply, Divide, Shift
 Review from last time CS152 Computer Architecture and Engineering Lecture 6 Verilog (finish) Multiply, Divide, Shift February 11, 2004 John Kubiatowicz (www.cs.berkeley.edu/~kubitron) lecture slides: http://www-inst.eecs.berkeley.edu/~cs152/
Review from last time CS152 Computer Architecture and Engineering Lecture 6 Verilog (finish) Multiply, Divide, Shift February 11, 2004 John Kubiatowicz (www.cs.berkeley.edu/~kubitron) lecture slides: http://www-inst.eecs.berkeley.edu/~cs152/
Lecture 8: Addition, Multiplication & Division
 Lecture 8: Addition, Multiplication & Division Today s topics: Signed/Unsigned Addition Multiplication Division 1 Signed / Unsigned The hardware recognizes two formats: unsigned (corresponding to the C
Lecture 8: Addition, Multiplication & Division Today s topics: Signed/Unsigned Addition Multiplication Division 1 Signed / Unsigned The hardware recognizes two formats: unsigned (corresponding to the C
Integer Multiplication and Division
 Integer Multiplication and Division COE 301 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals Presentation Outline
Integer Multiplication and Division COE 301 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals Presentation Outline
NUMBER OPERATIONS. Mahdi Nazm Bojnordi. CS/ECE 3810: Computer Organization. Assistant Professor School of Computing University of Utah
 NUMBER OPERATIONS Mahdi Nazm Bojnordi Assistant Professor School of Computing University of Utah CS/ECE 3810: Computer Organization Overview Homework 4 is due tonight Verify your uploaded file before the
NUMBER OPERATIONS Mahdi Nazm Bojnordi Assistant Professor School of Computing University of Utah CS/ECE 3810: Computer Organization Overview Homework 4 is due tonight Verify your uploaded file before the
COMPUTER ARITHMETIC (Part 1)
 Eastern Mediterranean University School of Computing and Technology ITEC255 Computer Organization & Architecture COMPUTER ARITHMETIC (Part 1) Introduction The two principal concerns for computer arithmetic
Eastern Mediterranean University School of Computing and Technology ITEC255 Computer Organization & Architecture COMPUTER ARITHMETIC (Part 1) Introduction The two principal concerns for computer arithmetic
More complicated than addition. Let's look at 3 versions based on grade school algorithm (multiplicand) More time and more area
 Multiplication More complicated than addition accomplished via shifting and addition More time and more area Let's look at 3 versions based on grade school algorithm 01010010 (multiplicand) x01101101 (multiplier)
Multiplication More complicated than addition accomplished via shifting and addition More time and more area Let's look at 3 versions based on grade school algorithm 01010010 (multiplicand) x01101101 (multiplier)
9 Multiplication and Division
 9 Multiplication and Division Multiplication is done by doing shifts and additions. Multiplying two (unsigned) numbers of n bits each results in a product of 2n bits. Example: 0110 x 0011 (6x3) At start,
9 Multiplication and Division Multiplication is done by doing shifts and additions. Multiplying two (unsigned) numbers of n bits each results in a product of 2n bits. Example: 0110 x 0011 (6x3) At start,
CS/COE 0447 Example Problems for Exam 2 Spring 2011
 CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
Module 2: Computer Arithmetic
 Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
carry in carry 1101 carry carry
 Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
Review: MULTIPLY HARDWARE Version 1. ECE4680 Computer Organization & Architecture. Divide, Floating Point, Pentium Bug
 ECE468 ALU-III.1 2002-2-27 Review: MULTIPLY HARDWARE Version 1 ECE4680 Computer Organization & Architecture 64-bit Multiplicand reg, 64-bit ALU, 64-bit Product reg, 32-bit multiplier reg Divide, Floating
ECE468 ALU-III.1 2002-2-27 Review: MULTIPLY HARDWARE Version 1 ECE4680 Computer Organization & Architecture 64-bit Multiplicand reg, 64-bit ALU, 64-bit Product reg, 32-bit multiplier reg Divide, Floating
Chapter 3: Arithmetic for Computers
 Chapter 3: Arithmetic for Computers Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point Computer Architecture CS 35101-002 2 The Binary Numbering
Chapter 3: Arithmetic for Computers Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point Computer Architecture CS 35101-002 2 The Binary Numbering
EE260: Logic Design, Spring n Integer multiplication. n Booth s algorithm. n Integer division. n Restoring, non-restoring
 EE 260: Introduction to Digital Design Arithmetic II Yao Zheng Department of Electrical Engineering University of Hawaiʻi at Mānoa Overview n Integer multiplication n Booth s algorithm n Integer division
EE 260: Introduction to Digital Design Arithmetic II Yao Zheng Department of Electrical Engineering University of Hawaiʻi at Mānoa Overview n Integer multiplication n Booth s algorithm n Integer division
Arithmetic Logic Unit
 Arithmetic Logic Unit A.R. Hurson Department of Computer Science Missouri University of Science & Technology A.R. Hurson 1 Arithmetic Logic Unit It is a functional bo designed to perform "basic" arithmetic,
Arithmetic Logic Unit A.R. Hurson Department of Computer Science Missouri University of Science & Technology A.R. Hurson 1 Arithmetic Logic Unit It is a functional bo designed to perform "basic" arithmetic,
Computer Architecture and Engineering Lecture 7: Divide, Floating Point, Pentium Bug
 Computer Architecture and Engineering Lecture 7: Divide, Floating Point, Pentium Bug September 17, 1997 Dave Patterson (http.cs.berkeley.edu/~patterson) lecture slides: http://www-inst.eecs.berkeley.edu/~cs152/
Computer Architecture and Engineering Lecture 7: Divide, Floating Point, Pentium Bug September 17, 1997 Dave Patterson (http.cs.berkeley.edu/~patterson) lecture slides: http://www-inst.eecs.berkeley.edu/~cs152/
Divide: Paper & Pencil CS152. Computer Architecture and Engineering Lecture 7. Divide, Floating Point, Pentium Bug. DIVIDE HARDWARE Version 1
 Divide: Paper & Pencil Computer Architecture and Engineering Lecture 7 Divide, Floating Point, Pentium Bug 1001 Quotient 1000 1001010 Dividend 1000 10 101 1010 1000 10 (or Modulo result) See how big a
Divide: Paper & Pencil Computer Architecture and Engineering Lecture 7 Divide, Floating Point, Pentium Bug 1001 Quotient 1000 1001010 Dividend 1000 10 101 1010 1000 10 (or Modulo result) See how big a
Timing for Ripple Carry Adder
 Timing for Ripple Carry Adder 1 2 3 Look Ahead Method 5 6 7 8 9 Look-Ahead, bits wide 10 11 Multiplication Simple Gradeschool Algorithm for 32 Bits (6 Bit Result) Multiplier Multiplicand AND gates 32
Timing for Ripple Carry Adder 1 2 3 Look Ahead Method 5 6 7 8 9 Look-Ahead, bits wide 10 11 Multiplication Simple Gradeschool Algorithm for 32 Bits (6 Bit Result) Multiplier Multiplicand AND gates 32
CSE 141 Computer Architecture Summer Session Lecture 3 ALU Part 2 Single Cycle CPU Part 1. Pramod V. Argade
 CSE 141 Computer Architecture Summer Session 1 2004 Lecture 3 ALU Part 2 Single Cycle CPU Part 1 Pramod V. Argade Reading Assignment Announcements Chapter 5: The Processor: Datapath and Control, Sec. 5.3-5.4
CSE 141 Computer Architecture Summer Session 1 2004 Lecture 3 ALU Part 2 Single Cycle CPU Part 1 Pramod V. Argade Reading Assignment Announcements Chapter 5: The Processor: Datapath and Control, Sec. 5.3-5.4
ECE260: Fundamentals of Computer Engineering
 Arithmetic for Computers James Moscola Dept. of Engineering & Computer Science York College of Pennsylvania Based on Computer Organization and Design, 5th Edition by Patterson & Hennessy Arithmetic for
Arithmetic for Computers James Moscola Dept. of Engineering & Computer Science York College of Pennsylvania Based on Computer Organization and Design, 5th Edition by Patterson & Hennessy Arithmetic for
Computer Arithmetic Multiplication & Shift Chapter 3.4 EEC170 FQ 2005
 Computer Arithmetic Multiplication & Shift Chapter 3.4 EEC170 FQ 200 Multiply We will start with unsigned multiply and contrast how humans and computers multiply Layout 8-bit 8 Pipelined Multiplier 1 2
Computer Arithmetic Multiplication & Shift Chapter 3.4 EEC170 FQ 200 Multiply We will start with unsigned multiply and contrast how humans and computers multiply Layout 8-bit 8 Pipelined Multiplier 1 2
CS/COE0447: Computer Organization
 CS/COE0447: Computer Organization and Assembly Language Chapter 3 Sangyeun Cho Dept. of Computer Science Five classic components I am like a control tower I am like a pack of file folders I am like a conveyor
CS/COE0447: Computer Organization and Assembly Language Chapter 3 Sangyeun Cho Dept. of Computer Science Five classic components I am like a control tower I am like a pack of file folders I am like a conveyor
CS/COE0447: Computer Organization
 Five classic components CS/COE0447: Computer Organization and Assembly Language I am like a control tower I am like a pack of file folders Chapter 3 I am like a conveyor belt + service stations I exchange
Five classic components CS/COE0447: Computer Organization and Assembly Language I am like a control tower I am like a pack of file folders Chapter 3 I am like a conveyor belt + service stations I exchange
Fast Arithmetic. Philipp Koehn. 19 October 2016
 Fast Arithmetic Philipp Koehn 19 October 2016 1 arithmetic Addition (Immediate) 2 Load immediately one number (s0 = 2) li $s0, 2 Add 4 ($s1 = $s0 + 4 = 6) addi $s1, $s0, 4 Subtract 3 ($s2 = $s1-3 = 3)
Fast Arithmetic Philipp Koehn 19 October 2016 1 arithmetic Addition (Immediate) 2 Load immediately one number (s0 = 2) li $s0, 2 Add 4 ($s1 = $s0 + 4 = 6) addi $s1, $s0, 4 Subtract 3 ($s2 = $s1-3 = 3)
Binary Adders. Ripple-Carry Adder
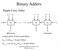 Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Τί είναι η αριθµητική Η/Υ?
 ΗΜΥ 312 -- ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΑΛΕΞΕΙΣ 14-15: Αριθμητική Η/Υ Διδάσκουσα: ΜΑΡΙΑ Κ. ΜΙΧΑΗΛ Αναπληρώτρια Καθηγήτρια, ΗΜΜΥ (mmichael@ucy.ac.cy) [Προσαρµογή από Computer Architecture, Computer
ΗΜΥ 312 -- ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΑΛΕΞΕΙΣ 14-15: Αριθμητική Η/Υ Διδάσκουσα: ΜΑΡΙΑ Κ. ΜΙΧΑΗΛ Αναπληρώτρια Καθηγήτρια, ΗΜΜΥ (mmichael@ucy.ac.cy) [Προσαρµογή από Computer Architecture, Computer
Integer Multiplication. Back to Arithmetic. Integer Multiplication. Example (Fig 4.25)
 Back to Arithmetic Before, we did Representation of integers Addition/Subtraction Logical ops Forecast Integer Multiplication Integer Division Floating-point Numbers Floating-point Addition/Multiplication
Back to Arithmetic Before, we did Representation of integers Addition/Subtraction Logical ops Forecast Integer Multiplication Integer Division Floating-point Numbers Floating-point Addition/Multiplication
Week 7: Assignment Solutions
 Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
COMPUTER ORGANIZATION AND DESIGN
 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication
Computer Organization and Structure. Bing-Yu Chen National Taiwan University
 Computer Organization and Structure Bing-Yu Chen National Taiwan University Arithmetic for Computers Addition and Subtraction Gate Logic and K-Map Method Constructing a Basic ALU Arithmetic Logic Unit
Computer Organization and Structure Bing-Yu Chen National Taiwan University Arithmetic for Computers Addition and Subtraction Gate Logic and K-Map Method Constructing a Basic ALU Arithmetic Logic Unit
Chapter 3 Arithmetic for Computers. ELEC 5200/ From P-H slides
 Chapter 3 Arithmetic for Computers 1 Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Chapter 3 Arithmetic for Computers 1 Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Lecture Topics. Announcements. Today: Integer Arithmetic (P&H ) Next: The MIPS ISA (P&H ) Consulting hours. Milestone #1 (due 1/26)
 Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: The MIPS ISA (P&H 2.1-2.14) 1 Announcements Consulting hours Milestone #1 (due 1/26) Milestone #2 (due 2/2) 2 1 Review: Integer Operations Internal
Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: The MIPS ISA (P&H 2.1-2.14) 1 Announcements Consulting hours Milestone #1 (due 1/26) Milestone #2 (due 2/2) 2 1 Review: Integer Operations Internal
Chapter 3 Arithmetic for Computers (Part 2)
 Department of Electr rical Eng ineering, Chapter 3 Arithmetic for Computers (Part 2) 王振傑 (Chen-Chieh Wang) ccwang@mail.ee.ncku.edu.tw ncku edu Depar rtment of Electr rical Eng ineering, Feng-Chia Unive
Department of Electr rical Eng ineering, Chapter 3 Arithmetic for Computers (Part 2) 王振傑 (Chen-Chieh Wang) ccwang@mail.ee.ncku.edu.tw ncku edu Depar rtment of Electr rical Eng ineering, Feng-Chia Unive
Chapter 3. Arithmetic Text: P&H rev
 Chapter 3 Arithmetic Text: P&H rev3.29.16 Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Chapter 3 Arithmetic Text: P&H rev3.29.16 Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
CPE300: Digital System Architecture and Design
 CPE300: Digital System Architecture and Design Fall 2011 MW 17:30-18:45 CBC C316 Arithmetic Unit 10122011 http://www.egr.unlv.edu/~b1morris/cpe300/ 2 Outline Recap Fixed Point Arithmetic Addition/Subtraction
CPE300: Digital System Architecture and Design Fall 2011 MW 17:30-18:45 CBC C316 Arithmetic Unit 10122011 http://www.egr.unlv.edu/~b1morris/cpe300/ 2 Outline Recap Fixed Point Arithmetic Addition/Subtraction
Organisasi Sistem Komputer
 LOGO Organisasi Sistem Komputer OSK 8 Aritmatika Komputer 1 1 PT. Elektronika FT UNY Does the calculations Arithmetic & Logic Unit Everything else in the computer is there to service this unit Handles
LOGO Organisasi Sistem Komputer OSK 8 Aritmatika Komputer 1 1 PT. Elektronika FT UNY Does the calculations Arithmetic & Logic Unit Everything else in the computer is there to service this unit Handles
Integer Arithmetic. Jinkyu Jeong Computer Systems Laboratory Sungkyunkwan University
 Integer Arithmetic Jinkyu Jeong (jinkyu@skku.edu) Computer Systems Laboratory Sungkyunkwan University http://csl.skku.edu EEE3050: Theory on Computer Architectures, Spring 2017, Jinkyu Jeong (jinkyu@skku.edu)
Integer Arithmetic Jinkyu Jeong (jinkyu@skku.edu) Computer Systems Laboratory Sungkyunkwan University http://csl.skku.edu EEE3050: Theory on Computer Architectures, Spring 2017, Jinkyu Jeong (jinkyu@skku.edu)
Chapter 3 Arithmetic for Computers
 Chapter 3 Arithmetic for Computers 1 Outline Signed and unsigned numbers (Sec. 3.2) Addition and subtraction (Sec. 3.3) Multiplication (Sec. 3.4) Division (Sec. 3.5) Floating point (Sec. 3.6) 2 Representation
Chapter 3 Arithmetic for Computers 1 Outline Signed and unsigned numbers (Sec. 3.2) Addition and subtraction (Sec. 3.3) Multiplication (Sec. 3.4) Division (Sec. 3.5) Floating point (Sec. 3.6) 2 Representation
COMPUTER ORGANIZATION AND. Edition. The Hardware/Software Interface. Chapter 3. Arithmetic for Computers
 ARM D COMPUTER ORGANIZATION AND Edition The Hardware/Software Interface Chapter 3 Arithmetic for Computers Modified and extended by R.J. Leduc - 2016 In this chapter, we will investigate: How integer arithmetic
ARM D COMPUTER ORGANIZATION AND Edition The Hardware/Software Interface Chapter 3 Arithmetic for Computers Modified and extended by R.J. Leduc - 2016 In this chapter, we will investigate: How integer arithmetic
What do all those bits mean now? Number Systems and Arithmetic. Introduction to Binary Numbers. Questions About Numbers
 Wht do ll those bits men now? bits (...) Number Systems nd Arithmetic or Computers go to elementry school instruction R-formt I-formt... integer dt number text chrs... floting point signed unsigned single
Wht do ll those bits men now? bits (...) Number Systems nd Arithmetic or Computers go to elementry school instruction R-formt I-formt... integer dt number text chrs... floting point signed unsigned single
Arithmetic Processing
 CS/EE 5830/6830 VLSI ARCHITECTURE Chapter 1 Basic Number Representations and Arithmetic Algorithms Arithmetic Processing AP = (operands, operation, results, conditions, singularities) Operands are: Set
CS/EE 5830/6830 VLSI ARCHITECTURE Chapter 1 Basic Number Representations and Arithmetic Algorithms Arithmetic Processing AP = (operands, operation, results, conditions, singularities) Operands are: Set
ECE331: Hardware Organization and Design
 ECE331: Hardware Organization and Design Lecture 9: Binary Addition & Multiplication Adapted from Computer Organization and Design, Patterson & Hennessy, UCB Pop Quiz! Using 4 bits signed integer notation:
ECE331: Hardware Organization and Design Lecture 9: Binary Addition & Multiplication Adapted from Computer Organization and Design, Patterson & Hennessy, UCB Pop Quiz! Using 4 bits signed integer notation:
Chapter 5 : Computer Arithmetic
 Chapter 5 Computer Arithmetic Integer Representation: (Fixedpoint representation): An eight bit word can be represented the numbers from zero to 255 including = 1 = 1 11111111 = 255 In general if an nbit
Chapter 5 Computer Arithmetic Integer Representation: (Fixedpoint representation): An eight bit word can be represented the numbers from zero to 255 including = 1 = 1 11111111 = 255 In general if an nbit
Chapter 3 Arithmetic for Computers
 Chapter 3 Arithmetic for Computers 1 Arithmetic Where we've been: Abstractions: Instruction Set Architecture Assembly Language and Machine Language What's up ahead: Implementing the Architecture operation
Chapter 3 Arithmetic for Computers 1 Arithmetic Where we've been: Abstractions: Instruction Set Architecture Assembly Language and Machine Language What's up ahead: Implementing the Architecture operation
Computer Architecture Chapter 3. Fall 2005 Department of Computer Science Kent State University
 Computer Architecture Chapter 3 Fall 2005 Department of Computer Science Kent State University Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point
Computer Architecture Chapter 3 Fall 2005 Department of Computer Science Kent State University Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point
Computer Architecture Set Four. Arithmetic
 Computer Architecture Set Four Arithmetic Arithmetic Where we ve been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What
Computer Architecture Set Four Arithmetic Arithmetic Where we ve been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What
Number Systems and Conversions UNIT 1 NUMBER SYSTEMS & CONVERSIONS. Number Systems (2/2) Number Systems (1/2) Iris Hui-Ru Jiang Spring 2010
 Contents Number systems and conversion Binary arithmetic Representation of negative numbers Addition of two s complement numbers Addition of one s complement numbers Binary s Readings Unit.~. UNIT NUMBER
Contents Number systems and conversion Binary arithmetic Representation of negative numbers Addition of two s complement numbers Addition of one s complement numbers Binary s Readings Unit.~. UNIT NUMBER
Math in MIPS. Subtracting a binary number from another binary number also bears an uncanny resemblance to the way it s done in decimal.
 Page < 1 > Math in MIPS Adding and Subtracting Numbers Adding two binary numbers together is very similar to the method used with decimal numbers, except simpler. When you add two binary numbers together,
Page < 1 > Math in MIPS Adding and Subtracting Numbers Adding two binary numbers together is very similar to the method used with decimal numbers, except simpler. When you add two binary numbers together,
Computer Architecture and Organization: L04: Micro-operations
 Computer Architecture and Organization: L4: Micro-operations By: A. H. Abdul Hafez Abdul.hafez@hku.edu.tr, ah.abdulhafez@gmail.com, hafez@research.iiit.ac.in 1 Outlines 1. Arithmetic microoperation 2.
Computer Architecture and Organization: L4: Micro-operations By: A. H. Abdul Hafez Abdul.hafez@hku.edu.tr, ah.abdulhafez@gmail.com, hafez@research.iiit.ac.in 1 Outlines 1. Arithmetic microoperation 2.
CS 64 Week 1 Lecture 1. Kyle Dewey
 CS 64 Week 1 Lecture 1 Kyle Dewey Overview Bitwise operation wrap-up Two s complement Addition Subtraction Multiplication (if time) Bitwise Operation Wrap-up Shift Left Move all the bits N positions to
CS 64 Week 1 Lecture 1 Kyle Dewey Overview Bitwise operation wrap-up Two s complement Addition Subtraction Multiplication (if time) Bitwise Operation Wrap-up Shift Left Move all the bits N positions to
Chapter 5: Computer Arithmetic. In this chapter you will learn about:
 Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop.
 CS 320 Ch 10 Computer Arithmetic The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop. Signed integers are typically represented in sign-magnitude
CS 320 Ch 10 Computer Arithmetic The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop. Signed integers are typically represented in sign-magnitude
Iterative Division Techniques COMPUTER ARITHMETIC: Lecture Notes # 6. University of Illinois at Chicago
 1 ECE 368 CAD Based Logic Design Instructor: Shantanu Dutt Department of Electrical and Computer Engineering University of Illinois at Chicago Lecture Notes # 6 COMPUTER ARITHMETIC: Iterative Division
1 ECE 368 CAD Based Logic Design Instructor: Shantanu Dutt Department of Electrical and Computer Engineering University of Illinois at Chicago Lecture Notes # 6 COMPUTER ARITHMETIC: Iterative Division
Lecture Topics. Announcements. Today: Integer Arithmetic (P&H ) Next: continued. Consulting hours. Introduction to Sim. Milestone #1 (due 1/26)
 Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: continued 1 Announcements Consulting hours Introduction to Sim Milestone #1 (due 1/26) 2 1 Overview: Integer Operations Internal representation
Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: continued 1 Announcements Consulting hours Introduction to Sim Milestone #1 (due 1/26) 2 1 Overview: Integer Operations Internal representation
VTU NOTES QUESTION PAPERS NEWS RESULTS FORUMS Arithmetic (a) The four possible cases Carry (b) Truth table x y
 Arithmetic A basic operation in all digital computers is the addition and subtraction of two numbers They are implemented, along with the basic logic functions such as AND,OR, NOT,EX- OR in the ALU subsystem
Arithmetic A basic operation in all digital computers is the addition and subtraction of two numbers They are implemented, along with the basic logic functions such as AND,OR, NOT,EX- OR in the ALU subsystem
UNIT-III COMPUTER ARTHIMETIC
 UNIT-III COMPUTER ARTHIMETIC INTRODUCTION Arithmetic Instructions in digital computers manipulate data to produce results necessary for the of activity solution of computational problems. These instructions
UNIT-III COMPUTER ARTHIMETIC INTRODUCTION Arithmetic Instructions in digital computers manipulate data to produce results necessary for the of activity solution of computational problems. These instructions
Learning Objectives. Binary over Decimal. In this chapter you will learn about:
 Ref Page Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction
Ref Page Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction
Two-Level CLA for 4-bit Adder. Two-Level CLA for 4-bit Adder. Two-Level CLA for 16-bit Adder. A Closer Look at CLA Delay
 Two-Level CLA for 4-bit Adder Individual carry equations C 1 = g 0 +p 0, C 2 = g 1 +p 1 C 1,C 3 = g 2 +p 2 C 2, = g 3 +p 3 C 3 Fully expanded (infinite hardware) CLA equations C 1 = g 0 +p 0 C 2 = g 1
Two-Level CLA for 4-bit Adder Individual carry equations C 1 = g 0 +p 0, C 2 = g 1 +p 1 C 1,C 3 = g 2 +p 2 C 2, = g 3 +p 3 C 3 Fully expanded (infinite hardware) CLA equations C 1 = g 0 +p 0 C 2 = g 1
CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit. A.R. Hurson 323 CS Building, Missouri S&T
 CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit A.R. Hurson 323 CS Building, Missouri S&T hurson@mst.edu 1 Outline Motivation Design of a simple ALU How to design
CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit A.R. Hurson 323 CS Building, Missouri S&T hurson@mst.edu 1 Outline Motivation Design of a simple ALU How to design
Introduction to Digital Logic Missouri S&T University CPE 2210 Multipliers/Dividers
 Introduction to Digital Logic Missouri S&T University CPE 2210 Multipliers/Dividers Egemen K. Çetinkaya Egemen K. Çetinkaya Department of Electrical & Computer Engineering Missouri University of Science
Introduction to Digital Logic Missouri S&T University CPE 2210 Multipliers/Dividers Egemen K. Çetinkaya Egemen K. Çetinkaya Department of Electrical & Computer Engineering Missouri University of Science
Today s Outline. CS152 Computer Architecture and Engineering Lecture 5. VHDL, Multiply, Shift
 Today s Outline CS152 Computer Architecture and Engineering Lecture 5 VHDL, Multiply, Shift September 14, 2001 John Kubiatowicz (http.cs.berkeley.edu/~kubitron) Review of Last lecture on-line lab notebook
Today s Outline CS152 Computer Architecture and Engineering Lecture 5 VHDL, Multiply, Shift September 14, 2001 John Kubiatowicz (http.cs.berkeley.edu/~kubitron) Review of Last lecture on-line lab notebook
Outline. Introduction to Structured VLSI Design. Signed and Unsigned Integers. 8 bit Signed/Unsigned Integers
 Outline Introduction to Structured VLSI Design Integer Arithmetic and Pipelining Multiplication in the digital domain HW mapping Pipelining optimization Joachim Rodrigues Signed and Unsigned Integers n-1
Outline Introduction to Structured VLSI Design Integer Arithmetic and Pipelining Multiplication in the digital domain HW mapping Pipelining optimization Joachim Rodrigues Signed and Unsigned Integers n-1
Computer Arithmetic Ch 8
 Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) (aritmeettis-looginen yksikkö) Does all
Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) (aritmeettis-looginen yksikkö) Does all
University of Illinois at Chicago. Lecture Notes # 13
 1 ECE 366 Computer Architecture Instructor: Shantanu Dutt Department of Electrical and Computer Engineering University of Illinois at Chicago Lecture Notes # 13 COMPUTER ARITHMETIC: Iterative Division
1 ECE 366 Computer Architecture Instructor: Shantanu Dutt Department of Electrical and Computer Engineering University of Illinois at Chicago Lecture Notes # 13 COMPUTER ARITHMETIC: Iterative Division
Arithmetic for Computers
 MIPS Arithmetic Instructions Cptr280 Dr Curtis Nelson Arithmetic for Computers Operations on integers Addition and subtraction; Multiplication and division; Dealing with overflow; Signed vs. unsigned numbers.
MIPS Arithmetic Instructions Cptr280 Dr Curtis Nelson Arithmetic for Computers Operations on integers Addition and subtraction; Multiplication and division; Dealing with overflow; Signed vs. unsigned numbers.
Computer Arithmetic Ch 8
 Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) Does all work in CPU (aritmeettis-looginen
Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) Does all work in CPU (aritmeettis-looginen
ΗΜΥ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ
 ΗΜΥ 312 -- ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΑΛΕΞΕΙΣ 14-15: Αριθμητική Η/Υ Διδάσκων: Χάρης Θεοχαρίδης Αναπληρωτής Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) [Προσαρμογή από Computer Architecture,
ΗΜΥ 312 -- ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΑΛΕΞΕΙΣ 14-15: Αριθμητική Η/Υ Διδάσκων: Χάρης Θεοχαρίδης Αναπληρωτής Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) [Προσαρμογή από Computer Architecture,
1010 2?= ?= CS 64 Lecture 2 Data Representation. Decimal Numbers: Base 10. Reading: FLD Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
 CS 64 Lecture 2 Data Representation Reading: FLD 1.2-1.4 Decimal Numbers: Base 10 Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Example: 3271 = (3x10 3 ) + (2x10 2 ) + (7x10 1 ) + (1x10 0 ) 1010 10?= 1010 2?= 1
CS 64 Lecture 2 Data Representation Reading: FLD 1.2-1.4 Decimal Numbers: Base 10 Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Example: 3271 = (3x10 3 ) + (2x10 2 ) + (7x10 1 ) + (1x10 0 ) 1010 10?= 1010 2?= 1
BINARY SYSTEM. Binary system is used in digital systems because it is:
 CHAPTER 2 CHAPTER CONTENTS 2.1 Binary System 2.2 Binary Arithmetic Operation 2.3 Signed & Unsigned Numbers 2.4 Arithmetic Operations of Signed Numbers 2.5 Hexadecimal Number System 2.6 Octal Number System
CHAPTER 2 CHAPTER CONTENTS 2.1 Binary System 2.2 Binary Arithmetic Operation 2.3 Signed & Unsigned Numbers 2.4 Arithmetic Operations of Signed Numbers 2.5 Hexadecimal Number System 2.6 Octal Number System
Chapter 3: part 3 Binary Subtraction
 Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
Topics. 6.1 Number Systems and Radix Conversion 6.2 Fixed-Point Arithmetic 6.3 Seminumeric Aspects of ALU Design 6.4 Floating-Point Arithmetic
 6-1 Chapter 6 Computer Arithmetic and the Arithmetic Unit Chapter 6: Computer Arithmetic and the Arithmetic Unit Topics 6.1 Number Systems and Radix Conversion 6.2 Fixed-Point Arithmetic 6.3 Seminumeric
6-1 Chapter 6 Computer Arithmetic and the Arithmetic Unit Chapter 6: Computer Arithmetic and the Arithmetic Unit Topics 6.1 Number Systems and Radix Conversion 6.2 Fixed-Point Arithmetic 6.3 Seminumeric
COMPUTER ARCHITECTURE AND ORGANIZATION. Operation Add Magnitudes Subtract Magnitudes (+A) + ( B) + (A B) (B A) + (A B)
 Computer Arithmetic Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation problems. The Addition,
Computer Arithmetic Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation problems. The Addition,
By, Ajinkya Karande Adarsh Yoga
 By, Ajinkya Karande Adarsh Yoga Introduction Early computer designers believed saving computer time and memory were more important than programmer time. Bug in the divide algorithm used in Intel chips.
By, Ajinkya Karande Adarsh Yoga Introduction Early computer designers believed saving computer time and memory were more important than programmer time. Bug in the divide algorithm used in Intel chips.
EE 109 Unit 6 Binary Arithmetic
 EE 109 Unit 6 Binary Arithmetic 1 2 Semester Transition Point At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
EE 109 Unit 6 Binary Arithmetic 1 2 Semester Transition Point At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
CS/COE 0447 Example Problems for Exam 2 Fall 2010
 CS/COE 0447 Example Problems for Exam 2 Fall 2010 1. This time, consider a non-leaf function lisa. This function has no arugments or return value. The return address is on the stack at offset 12 and the
CS/COE 0447 Example Problems for Exam 2 Fall 2010 1. This time, consider a non-leaf function lisa. This function has no arugments or return value. The return address is on the stack at offset 12 and the
UNIT - I: COMPUTER ARITHMETIC, REGISTER TRANSFER LANGUAGE & MICROOPERATIONS
 UNIT - I: COMPUTER ARITHMETIC, REGISTER TRANSFER LANGUAGE & MICROOPERATIONS (09 periods) Computer Arithmetic: Data Representation, Fixed Point Representation, Floating Point Representation, Addition and
UNIT - I: COMPUTER ARITHMETIC, REGISTER TRANSFER LANGUAGE & MICROOPERATIONS (09 periods) Computer Arithmetic: Data Representation, Fixed Point Representation, Floating Point Representation, Addition and
Thomas Polzer Institut für Technische Informatik
 Thomas Polzer tpolzer@ecs.tuwien.ac.at Institut für Technische Informatik Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers VO
Thomas Polzer tpolzer@ecs.tuwien.ac.at Institut für Technische Informatik Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers VO
Review: MIPS Organization
 1 MIPS Arithmetic Review: MIPS Organization Processor Memory src1 addr 5 src2 addr 5 dst addr 5 write data Register File registers ($zero - $ra) bits src1 data src2 data read/write addr 1 1100 2 30 words
1 MIPS Arithmetic Review: MIPS Organization Processor Memory src1 addr 5 src2 addr 5 dst addr 5 write data Register File registers ($zero - $ra) bits src1 data src2 data read/write addr 1 1100 2 30 words
Integer Multiplication and Division
 Integer Multiplication and Division for ENCM 369: Computer Organization Steve Norman, PhD, PEng Electrical & Computer Engineering Schulich School of Engineering University of Calgary Winter Term, 208 Integer
Integer Multiplication and Division for ENCM 369: Computer Organization Steve Norman, PhD, PEng Electrical & Computer Engineering Schulich School of Engineering University of Calgary Winter Term, 208 Integer
Least Common Multiple (LCM)
 Least Common Multiple (LCM) Task: Implement an LCM algorithm that is able to handle any combination of 8-bit (sign bit included) numbers. Use two's complement format to represent negative values. Provide
Least Common Multiple (LCM) Task: Implement an LCM algorithm that is able to handle any combination of 8-bit (sign bit included) numbers. Use two's complement format to represent negative values. Provide
Arithmetic Logic Unit. Digital Computer Design
 Arithmetic Logic Unit Digital Computer Design Arithmetic Circuits Arithmetic circuits are the central building blocks of computers. Computers and digital logic perform many arithmetic functions: addition,
Arithmetic Logic Unit Digital Computer Design Arithmetic Circuits Arithmetic circuits are the central building blocks of computers. Computers and digital logic perform many arithmetic functions: addition,
HW2 solutions You did this for Lab sbn temp, temp,.+1 # temp = 0; sbn temp, b,.+1 # temp = -b; sbn a, temp,.+1 # a = a (-b) = a + b;
 HW2 solutions 3.10 Pseuodinstructions What is accomplished Minimum sequence of Mips Move $t5, $t3 $t5=$t3 Add $t5, $t3, $0 Clear $t5 $t5=0 Xor $t5, $t5, $t5 Li $t5, small $t5=small Addi $t5, $0, small
HW2 solutions 3.10 Pseuodinstructions What is accomplished Minimum sequence of Mips Move $t5, $t3 $t5=$t3 Add $t5, $t3, $0 Clear $t5 $t5=0 Xor $t5, $t5, $t5 Li $t5, small $t5=small Addi $t5, $0, small
Experiment Objectives. 2. Preparation. 3. Tasks. 3.1 Task A: String to Integer Conversion
 Experiment 3 1. Objectives In this experiment, you will learn more AVR instructions by writing AVR assembly programs to do string-to-number conversion, positional multiplication, positional division, and
Experiment 3 1. Objectives In this experiment, you will learn more AVR instructions by writing AVR assembly programs to do string-to-number conversion, positional multiplication, positional division, and
Chapter 5: Computer Arithmetic
 Slide 1/29 Learning Objectives Computer Fundamentals: Pradeep K. Sinha & Priti Sinha In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations
Slide 1/29 Learning Objectives Computer Fundamentals: Pradeep K. Sinha & Priti Sinha In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations
CHW 261: Logic Design
 CHW 261: Logic Design Instructors: Prof. Hala Zayed Dr. Ahmed Shalaby http://www.bu.edu.eg/staff/halazayed14 http://bu.edu.eg/staff/ahmedshalaby14# Slide 1 Slide 2 Slide 3 Digital Fundamentals CHAPTER
CHW 261: Logic Design Instructors: Prof. Hala Zayed Dr. Ahmed Shalaby http://www.bu.edu.eg/staff/halazayed14 http://bu.edu.eg/staff/ahmedshalaby14# Slide 1 Slide 2 Slide 3 Digital Fundamentals CHAPTER
McGill University Faculty of Engineering FINAL EXAMINATION Fall 2007 (DEC 2007)
 McGill University Faculty of Engineering FINAL EXAMINATION Fall 2007 (DEC 2007) VERSION 1 Examiner: Professor T.Arbel Signature: INTRODUCTION TO COMPUTER ENGINEERING ECSE-221A 6 December 2007, 1400-1700
McGill University Faculty of Engineering FINAL EXAMINATION Fall 2007 (DEC 2007) VERSION 1 Examiner: Professor T.Arbel Signature: INTRODUCTION TO COMPUTER ENGINEERING ECSE-221A 6 December 2007, 1400-1700
Numbering systems. Dr Abu Arqoub
 Numbering systems The decimal numbering system is widely used, because the people Accustomed (معتاد) to use the hand fingers in their counting. But with the development of the computer science another
Numbering systems The decimal numbering system is widely used, because the people Accustomed (معتاد) to use the hand fingers in their counting. But with the development of the computer science another
DLD VIDYA SAGAR P. potharajuvidyasagar.wordpress.com. Vignana Bharathi Institute of Technology UNIT 1 DLD P VIDYA SAGAR
 UNIT I Digital Systems: Binary Numbers, Octal, Hexa Decimal and other base numbers, Number base conversions, complements, signed binary numbers, Floating point number representation, binary codes, error
UNIT I Digital Systems: Binary Numbers, Octal, Hexa Decimal and other base numbers, Number base conversions, complements, signed binary numbers, Floating point number representation, binary codes, error
An instruction set processor consist of two important units: Data Processing Unit (DataPath) Program Control Unit
 DataPath Design An instruction set processor consist of two important units: Data Processing Unit (DataPath) Program Control Unit Add & subtract instructions for fixed binary numbers are found in the
DataPath Design An instruction set processor consist of two important units: Data Processing Unit (DataPath) Program Control Unit Add & subtract instructions for fixed binary numbers are found in the
