6.2 Volumes of Revolution: The Disk Method
|
|
|
- Wilfrid Carson
- 5 years ago
- Views:
Transcription
1 mth ppliction: volumes by disks: volume prt ii 6 6 Volumes of Revolution: The Disk Method One of the simplest pplictions of integrtion (Theorem 6) nd the ccumultion process is to determine so-clled volumes of revolution In this section we will concentrte on method known s the disk method Solids of Revolution If region in the plne is revolved bout line in the sme plne, the resulting object is solid of revolution, nd the line is clled the xis of revolution The following sitution is typicl of the problems we will encounter Solids of Revolution from Ares Under Curves Suppose tht y = f (x) is continuous (non-negtive) function on the intervl [, b] Rotte the region under the f between x = nd x = b round the the x-xis nd determine the volume of the resulting solid of revolution See Figure 6 f (x i ) y = f (x) f (x i ) x i b x i b Once we know the cross-sectionl res of the solid, we cn use Theorem 6 to determine the volume But s Figure 6 shows, when the point (x i, f (x i )) on the curve is rotted bout the x-xis, it forms circulr cross-section of rdius R = f (x i ) Therefore, the cross-sectionl re t x i is Figure 6: Left: The region under the continuous curve y = f (x) on the intervl [, b] Right: The solid generted by rotting the region bout the x-xis Note: The point (x i, f (x i )) on the curve trces out circulr crosssection of rdius r = f (x i ) when rotted A(x i )=pr [ f (x i )] Since f is continuous, so is p[ f (x)] nd consequently Theorem 6 pplies Volume of Solid of Revolution = A(x) dx = p[ f (x)] dx Of course, we could use this sme process if we rotted the region bout the y-xis nd integrted long the y-xis We gther these results together nd stte them s theorem THEOREM 6 (The Disk Method) If V is the volume of the solid of revolution determined by rotting the continuous function f (x) on the intervl [, b] bout the x-xis, then V [ f (x)] dx (6) If V is the volume of the solid of revolution determined by rotting the continuous function f (y) on the intervl [c, d] bout the y-xis, then Z d V [ f (y)] dy (6) c Another Development of the Disk Method Using Riemnn Sums Insted of using Theorem 6, we could obtin Theorem 6 directly by using the subdivide nd conquer strtegy once gin Since we will use this strtegy in lter situtions, let s quickly go through the rgument here There re often severl wys to prove result in mthemtics I hope one of these two will resonte with you Volumetex Version: Mitchell-//8::
2 mth ppliction: volumes by disks: volume prt ii 7 As bove, we strt with continuous function on [, b] This time, though, we crete regulr prtition of [, b] using n intervls nd drw the corresponding pproximting rectngles of equl width Dx In left hlf of Figure 6 we hve drwn single representtive pproximting rectngle on the ith subintervl f (x i ) Dx b y = f (x) Dx b f (x i ) y = f (x) Rotting ech representtive rectngle cretes representtive disk (cylinder) of rdius R = f (x i ) (See the right hlf of Figure 6) The volume of this cylinder is given by (6) Volume of Cylinder =(re of the bse) height In this cse when the disk is situted on its side, we think of the height s the width Dx of the disk Moreover, since the bse is circle, its re is pr = p[ f (x i )] so Volume of representtive disk = DV i [ f (x i )] Dx To determine the volume of entire solid of revolution, we tke ech pproximting rectngle, form the corresponding disks (see the middle pnel of Figure 6) nd sum the resulting volumes, it genertes representtive disk whose volume is DV R Dx [R(x i )] Dx Figure 6: Left: The region under the continuous curve y = f (x) on the intervl [, b] nd representtive rectngle Right: The disk (cylinder) of rdius R = f (x i ) generted by rotting the representtive rectngle bout the x-xis The volume or this disk is pr w [ f (x i )] Dx Figure 6: A generl solid of revolution nd its pproximtion by series of n disks (Digrm from Lrson & Edwrds) Approximting the volume of the entire solid by n such disks (see the righthnd pnel of Figure 6) of width Dx nd rdius f (x i ) produces Riemnn sum Volume of Revolution n  i= p[ f (x i )] Dx n  i= [ f (x i )] Dx (6) As usul, to improve the pproximtion we let the number of subdivisions n! nd tke limit Recll from our erlier work with Riemnn sums, this limit exists Volumetex Version: Mitchell-//8::
3 mth ppliction: volumes by disks: volume prt ii 8 becuse [ f (x)] is continuous on [, b] since f (x) is continuous there Volume of Revolution = lim n p n! Â i= [ f (x i )] Dx [ f (x)] dx (6) where we hve used the fct tht the limit of Riemnn sum is definite integrl This is the sme result we obtined in Theorem 6 Ee could use this sme process if we rotted the region bout the y-xis nd integrted long the y-xis Stop! Notice how we used the subdivide nd conquer process to pproximte the quntity we wish to determine Tht is we hve subdivided the volume into pproximting disks whose volume we know how to compute We hve then refined this pproximtion by using finer nd finer subdivisions Tking the limit of this process provides the nswer to our question Identifying tht limit with n integrl mkes it possible to esily (!) compute the volume in question OK, time for some exmples I ll dmit it is hrd to drw figures like Figure 6 However, drwing representtive rectngle for the region in question, s in the left hlf of Figure 6 is usully sufficient to set up the required volume integrl Exmples Let s strt with couple of esy ones EXAMPLE 6 Let y = f (x) =x on the intervl [, ] Rotte the region between the curve nd the x-xis round the x-xis nd find the volume of the resulting solid Solution Using Theorem 6 Wow, tht ws esy! Z V [ f (x)] dx [x ] dx x EXAMPLE 6 Let y = f (x) =x on the intervl [, ] Rotte the region between the curve nd the y-xis round the y-xis nd find the volume of the resulting solid Solution The region is not the sme one s in Exmple 6 It lies between the y-xis nd the curve, not the x-xis See Figure 6 Since the rottion is bout the y-xis, we need to solve for x s function of y Since y = x, then x y Notice tht the region lies over the intervl [, ] on the y-xis now Using Theorem 6 Z d Z V [g(y)] dy [ p y] dy y c EXAMPLE 6 Find the volume of sphere of rdius r which cn be obtined by rotting the semi-circle f (x) r x bout the x-xis f (x) =x f (x) =x Figure 6: Left: A representtive rectngle for the curve y = x Right: A representtive circulr slice for the curve y = x rotted bout the x-xis f (x) =x x y Figure 6: Left: A representtive rectngle for the region between the curve y = x (x y) nd the y-xis Right: A representtive circulr slice for the curve x y rotted bout the x-xis Volumetex Version: Mitchell-//8::
4 mth ppliction: volumes by disks: volume prt ii 9 r r Figure 6: Left: A representtive rectngle for the curve y r x Right: A representtive circulr slice for the sphere tht results when rotting the semi-circle bout the x-xis Solution Using Theorem 6 Z r V [ f (x)] dx [ p r x ] dx r Z r r r x r pple r r r x dx x r r r + r Amzing! We hve derived the volume formul of sphere from the volume by disks formul YOU TRY IT 69 Find the volume of cone of rdius r nd height h by rotting the line through (, ) nd (r, h) bout the y-xis (See Figure 66) EXAMPLE 6 (Two Pieces) Consider the region enclosed by the curves y x, y = 6 x, nd the x-xis Rotte this region bout the x-xis nd find the resulting volume Solution It is importnt to sketch the region to see the reltionship between the curves Py prticulr ttention to the bounding curves Drw representtive rectngles This will help you set up the pproprite integrls It is less importnt to try to drw very ccurte three-dimensionl picture h Figure 66: Determine the volume of cone of rdius r nd height h r 6 6 First determine where the curves intersect: Obviously y x meets the x-xis t x = nd y = 6 x meets the x-xis t x = 6 For y = 6 x nd y x, 6 x x ) 6 x + x = x ) x x + 6 =(x )(x + 9) = ) x =, (x = 9 is not in the domin) From Figure 67 we see tht the solid is mde up of two seprte pieces (the top curve chnges t x = ) nd ech requires its own integrl Using Theorem 6 Figure 67: Left: The region enclosed by the curves y x, y = 6 x, nd the x-xis nd two representtive rectngles Right: The resulting solid of revolution bout the x-xis is formed by two distinct pieces ech requiring its own integrl Volumetex Version: Mitchell-//8::
5 mth ppliction: volumes by disks: volume prt ii Z V [ p Z 6 x] dx + p [6 x] dx Z Z 6 xdx+ p p(6 x) x + =(8p )+ [6 x] dx 6 ( 8p) Note: We used mentl djustment to do the second integrl (with u = 6 x nd du = dx) Overll, the integrtion is esy once the problem is set up correctly Be sure you hve the correct region EXAMPLE 66 (One Piece: Two integrls) Reconsider the sme region s in Exmple 6 enclosed by the curves y x, y = 6 x, nd the x-xis Now rotte this region bout the y-xis insted nd find the resulting volume Solution OK, the region is the sme s bove Here is where you hve to be very creful Since the rottion is bout the y-xis, the strips re horizontl this time Notice tht there re two strips When this region is rotted bout the y-xis, the solid will hve hollowed out center portion (see Figure 68) Thus, we must tke the outer region formed by the curve y = 6 x nd subtrct the inner region formed by y x from it 6 Since the rottion is bout the y-xis, to use the disk method we need to write the curves in the form x s function of y We hve Figure 68: Left: The region enclosed by the curves y x, y = 6 x, nd the x-xis nd two representtive rectngles Right: The resulting solid of revolution bout the x-xis ( volcno ) is formed by two distinct pieces ech requiring its own integrl y x ) x = y nd y = 6 x ) x = 6 y The outer curve is x = 6 y nd the inner curve is x = y from the perspective of the y-xis From the previous problem we lredy know the intersection points However we need their y-coordintes When x = the corresponding y-coordinte (using either y x or y = 6 x) is y = The other coordinte is y = So this time using Theorem 6 (note the subtrction of the inner volume) V = Outer Volume = = Z [6 y] dy p p(6 y) 6p = 66p Inner Volume py 6p Z [y ] dy p Whew! Tht s lot of things to process Getting cler picture of the region is crucil Even if you never drw the three-dimensionl version, understnding the Volumetex Version: Mitchell-//8::
6 mth ppliction: volumes by disks: volume prt ii representtive rectngles is criticl In this cse the representtive rectngles did not extend from the bottom to the top curve (ie, the left to the right), but rther from the y-xis to ech curve seprtely to represent the outer solid nd the inner solid Cution! We wrote the volume of the solid s the outer minus inner volume: Z Z V [6 y] dy p [y ] dy Since the intervl is the sme for both integrls, we could hve written this s Z V [6 y] [y ] dy where ech individul rdius is squred seprtely If you do combine the integrls, you cnnot squre the difference of the two rdii: Z V 6 [6 y y ] dy becuse [6 y] [y ] 6=[6 y y ] You ve been wrned! Look, there re two situtions you need to distinguish when multiple curves re used for solid of revolution The curves might crete two pieces which sum together to crete the entire solid in which cse you will need to dd integrls together to find the volume (see Figure 67) Or the curves might be situted so tht resulting solid is formed by hollowing out one solid from nother in which cse you will need to subtrct one integrl from nother (see Figure 68) This is why sketch of the position of the curves reltive to the xis of rottion is criticl Let s do couple more EXAMPLE 67 Consider the region enclosed by the curves y x, y = x x-xis Rotte this region bout the x-xis nd find the resulting volume, nd the Solution Is this the sum of two integrls or is it difference of two integrls? First determine where the curves intersect: Obviously y x meets the x-xis t x = nd y = x meets the x-xis t x = Now y = x nd y x intersect when x x ) x x + = x ) x x + =(x )(x + ) = ) x =, (not x = ) From the sketch in Figure 69 if revolved bout the x-xis will result in solid tht hs been prtilly hollowed out ( cone hs been removed) This requires Outer Inner Figure 69: Left: The region enclosed by the curves y x, y = x, nd the x-xis When rotted bout the x-xis, one region must be subtrcted from the other Insted of using representtive rectngles, we simply indicte the pproprite rdii with rrows Volumetex Version: Mitchell-//8::
7 mth ppliction: volumes by disks: volume prt ii difference of integrls Using Theorem 6 V = Outer Volume Z Z x [ p x] dx p xdx 8p =(8p )+ = 6p Inner Volume Z [x ] dx Z p [x ] dx p(x ) EXAMPLE 68 Agin consider the region enclosed by the curves y x, y = x x-xis This time rotte the region bout the y-xis nd find the resulting volume, nd the Solution Is this the sum of two integrls or is it difference of two integrls? Since the rottion is bout the y-xis, the rdii of the respective regions re horizontl, see Figure 6 This is gin difference of two integrls Trnslting the curves into functions of y we hve x = y Inner, x = y +, nd y = Outer (the x-xis) The curves intersect the x-xis t y = We ve seen tht the line nd squre root function meet when x = since x = y + there, then the y-coordinte of the intersection is y = Using Theorem 6 Figure 6: The region enclosed by the curves y Z x, y = x, nd the Z x-xis nd representtive rdii When V = Outer Volume Inner Volume [y + ] dy p [y ] dy rotted bout the y-xis, one region must be subtrcted from the other p(y + ) py = 6p = = 8p 8p p EXAMPLE 69 Consider the region enclosed by the curves y = e x, x = nd the y-xis Rotte the region bout the y-xis nd find the resulting volume Solution Is this the sum of two integrls or is it difference of two integrls? Since the rottion is bout the y-xis, the rdii of the respective regions re horizontl, see Figure 6 This is gin difference of two integrls Trnslting the curves into functions of y we see y = e x becomes x = ln y Notice tht x = ln y meets the y-xis t nd it meets the line x = t y = e The solid formed by the region between the y-xis nd the curve x = ln y must be subtrcted from the ordinry cylinder formed by rotting the line x = bout the y-xis This cylinder hs rdius nd height e so its volume is v = p() e e (We could lso find this by integrting, but why bother) So Using Theorem 6 V = Outer Volume Inner Volume e p Z e [ln y] dy =??? e Inner Outer y = e x or x = ln y Figure 6: The region enclosed by the curves y = e x, x = nd the y-xis Rotte the region bout the y-xis nd find the resulting volume Volumetex Version: Mitchell-//8::
8 mth ppliction: volumes by disks: volume prt ii Since we don t know n ntiderivtive for (ln x) we re stuck (By the wy, notice tht the limits of integrtion for the integrl re from to e, not to e) So we will hve to invent nother method of finding such volumes if we re to solve this problem This shows the importnce of hving wide-vriety of methods for solving single problem YOU TRY IT 6 Let R be the entire region enclosed by y = x nd y = x in the upper hlf-plne Sketch the region Rotte R bout the x-xis nd find the resulting volume (Answer: 6 p) YOU TRY IT 6 Let R be the region enclosed by y = x nd y = x () Rottion bout the x-xis Find the volume of the hollowed-out solid generted by revolving R bout the x-xis (Answer: 6p/) (b) Rottion bout the y-xis Find the volume of the solid generted by revolving R bout the y-xis by using the disk method nd integrting long the y-xis (Answer: 8p/) webwork: Click to try Problems 8 through 86 Use guest login, if not in my course Volumetex Version: Mitchell-//8::
9 mth ppliction: volumes by disks: volume prt ii 6 Optionl: Rottion About Other Axes It is reltively esy to dpt the disk method to finding volumes of solids of revolution using other horizontl or verticl xes The key steps re to determine the rdii of the slices nd express them in terms of the correct vrible A couple of exmples should give you the ide EXAMPLE 6 Consider the region enclosed by the curves y = x this region bout the line y = nd find the resulting volume x nd y = Rotte Solution The two curves meet when x x = ) x x =(x )(x + ) = ) x =, The prbol nd the line re esy to sketch; see Figure 6 on the left y = y = x x y = A representtive rdius extends from the line y = to the curve y = x x The length of rdius is the difference between these two vlues, tht is, the rdius of circulr cross-section perpendiculr to the line y = is Since cross-section is circle, its re is r = (x x) = + x x A = A(x) =pr ( + x x ) Since we know the cross-sectionl re, we cn use Theorem 6 to find the volume Figure 6: Left: The region enclosed by the curves y = x x nd y = Since the xis of revolution is y =, representtive rdius extends from the line y = to the curve y = x x Right: The resulting solid of revolution bout the line y = V = Z A(x) dx Z ( + x x ) dx 9 + x x x + x ) dx 9x + 6x x x + x pple = p EXAMPLE 6 Consider the region enclosed by the curves x = y nd x = this region bout the line x = nd find the resulting volume y Rotte Volumetex Version: Mitchell-//8::
10 mth ppliction: volumes by disks: volume prt ii x = y x = y x = x = Figure 6: Left: The region enclosed by the curves x = y nd x = y nd two representtive rdii emnting from the xis of rottion x = Right: The resulting hollowed out solid of revolution bout the line x = looks like doughnut Solution The two curves meet when y = y ) y = ) y = ± The region is esy to sketch; see Figure 6 on the left An outer representtive rdius extends from the line x = to the curve x = y nd n inner representtive rdius extends from the line x = to x = y The length of representtive rdius is the difference between the corresponding pirs of vlues The outer rdius is R = y nd the inner rdius is ( y )= + y The integrtion will tke plce long the y-xis on the intervl [, ] becuse the disks re horizontl when points re rotted bout the line x = Since we know the cross-sections re circles, we cn use Theorem 6 to find the volume V = Outer Volume Inner Volume Z Z Z 8y pple 8 ( y ) dy p Z 9 6y + y dy p 8 8y dy 8y ( + y ) dy Z + y + y dy Becuse the intervl of integrtion ws the sme for both the inner nd outer volumes, we re ble to combine the two integrls which gretly simplified the integrtion nd evlution If you understnd this problem, you re in good shpe YOU TRY IT 6 Let R be the region enclosed by y = x, x =, nd the x-xis Drw the region () Rotte R bout the x-xis nd find the resulting volume (Answer: 8p/7) (b) Rotte R bout the line y = 9 nd find the resulting volume (Answer: 76p/7) (c) Rotte R bout the line x = nd find the resulting volume (Answer: 6p/) YOU TRY IT 6 Drw the region R in the first qudrnt enclosed by y = x, y = the x-xis x nd () Rotte R bout the x-xis nd find the resulting volume [Is it the sum of two integrls or outside minus inside?] (b) Rotte R bout the y-xis nd find the resulting volume [Is it the sum of two integrls or outside minus inside?] YOU TRY IT 6 Let S be the region in the first qudrnt enclosed by y = x, y = the y-xis () Rotte S bout the x-xis [Is it the sum of two integrls or outside minus inside?] (b) Rotte S bout the y-xis [Is it the sum of two integrls or outside minus inside?] x nd Volumetex Version: Mitchell-//8::
11 mth ppliction: volumes by disks: volume prt ii 6 YOU TRY IT 6 Let R be the region in the upper hlf-plne bounded by y x +, the x-xis nd the line y = x Find the volume resulting when R is rotted round the x-xis Remember: Outside minus inside How mny integrls do you need? YOU TRY IT 66 A smll cnl bouy is formed by tking the region in the first qudrnt bounded by the y-xis, the prbol y = x, nd the line y = x nd rotting it bout the y-xis (Units re feet) Find the volume of this bouy (Answer: p cubic feet) YOU TRY IT 67 Just set up the integrls for ech of the following volume problems Simplify the integrnds where possible Use figures below () R is the region enclosed by y = x, y = x +, nd the y-xis in the first qudrnt Rotte R bout the x-xis (b) Sme R, but rotte round the y-xis (c) Sme R, but rotte round the line y = (d) S is the region enclosed by y = x + x +, y = x, the y-xis, nd the x-xis in the first qudrnt Rotte S bout the x-xis (e) T is the region enclosed by y = x + x +, y = x, nd the x-xis in the first qudrnt Rotte T bout the x-xis (f ) R is the region enclosed by y = x + nd y = x Rotte R bout the x-xis (g) Sme R, but rotte round the line y = (h) S is the region enclosed by y = x + nd y = x in the first qudrnt Rotte S bout the y-xis (i) T is the region enclosed by y x, y = x, the y-xis nd the x-xis Rotte T bout the y-xis (j) V is the region enclosed by y x, y = x, nd the x-xis Rotte V bout the y-xis (k) Sme V, but rotte round the x-xis (l) Hrd: Sme V, but rotte round the line y = Figure 6: The region for you try it 6 6 c 6 d e Figure 6: The regions for you try it 67 R S T i l f g h R R S T V 6 Volumetex Version: Mitchell-//8::
12 mth ppliction: volumes by disks: volume prt ii 7 Solution Here re the solutions before the integnds hve been simplified Remember, you should simplify ech integrnd before ctully integrting Z () p (c) p Z Z (x + ) dx p ( x ) dx p Z (e) p (x ) dx + p (g) Homework Z Z Z Z (i) p (y + ) dy + p ( y) dy (j) p Z ( y) dy p Z (l) p dx p Z ( Z Z (x ) dx (b) p ( (x + )) dx (d) p Z ( x + x + ) dx (f ) Homework (y + ) dy (k) p p x ) dx + ( p Z y) dy p (y ) dy ( x + x + ) dx p Z (h) p ( p y) dy p Z Z p y (x ) dx dy Z ( p Z x ) dx + p ( x) dx pple Z Z p dx p ( ( x)) dx YOU TRY IT 68 (Rottion bout the x-xis) Let R be the region in the first qudrnt enclosed by y x, y = x 7 nd the x-xis Sketch the region Rotte R bout the x-xis nd find the resulting volume (Answer: 6/p) YOU TRY IT 69 Let R be the entire region enclosed by y = x nd y = x in the upper hlf-plne Sketch the region Rotte R bout the x-xis nd find the resulting volume (Answer: 6 p) YOU TRY IT 6 (Rottion bout the y-xis) Let R be the region enclosed by the x-xis, y = p x, nd y = x Rotte R bout the y-xis nd find the volume (Answer: p/) YOU TRY IT 6 (Rottion bout line prllel to the x-xis) Find the volume of the hollowedout solid generted by revolving R bout the line y = (Answer: p/) YOU TRY IT 6 (Rottion bout line prllel to the x-xis) Let R be the region enclosed by y = x nd the x-xis Rotte R bout the line y = nd find the resulting volume (Answer: 6p/) YOU TRY IT 6 Extr Fun () Let R be the region enclosed by y = rctn x, y /, nd the y-xis Find the re of R Hint: Only integrtion long one xis is possible t this point (Answer: ln p = ln ) (b) Rotte R bout the y-xis nd find the resulting volume Use trig identity for tn q (Answer: p p /) YOU TRY IT 6 Here re few more: () Let y = x on [, ], where > Let R be the region under the curve over this intervl Rotte R bout the x-xis Wht vlue of gives volume of p/? (Answer: = ) (b) Wht hppens to the volume if!? Does the volume get infinitely lrge? Use limits to nswer the question (c) Insted rotte R bout the y-xis Wht vlue of gives volume of p/? This is prticulrly esy to do by shells! (Answer: = /) (d) Insted rotte R bout the line y = p (Answer: p e ) If we let = e wht is the resulting volume? YOU TRY IT 6 Let R be the region enclosed by y x, y =, nd the y-xis () Rotte R bout the x-xis nd find the resulting volume (Answer: 8p) (b) Rotte R bout the line y = nd find the resulting volume (Answer: 8p/) (c) Rotte R bout the line y = nd find the resulting volume (Answer: p/) Volumetex Version: Mitchell-//8::
a < a+ x < a+2 x < < a+n x = b, n A i n f(x i ) x. i=1 i=1
 Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
B. Definition: The volume of a solid of known integrable cross-section area A(x) from x = a
 Mth 176 Clculus Sec. 6.: Volume I. Volume By Slicing A. Introduction We will e trying to find the volume of solid shped using the sum of cross section res times width. We will e driving towrd developing
Mth 176 Clculus Sec. 6.: Volume I. Volume By Slicing A. Introduction We will e trying to find the volume of solid shped using the sum of cross section res times width. We will e driving towrd developing
6.3 Volumes. Just as area is always positive, so is volume and our attitudes towards finding it.
 6.3 Volumes Just s re is lwys positive, so is volume nd our ttitudes towrds finding it. Let s review how to find the volume of regulr geometric prism, tht is, 3-dimensionl oject with two regulr fces seprted
6.3 Volumes Just s re is lwys positive, so is volume nd our ttitudes towrds finding it. Let s review how to find the volume of regulr geometric prism, tht is, 3-dimensionl oject with two regulr fces seprted
If f(x, y) is a surface that lies above r(t), we can think about the area between the surface and the curve.
 Line Integrls The ide of line integrl is very similr to tht of single integrls. If the function f(x) is bove the x-xis on the intervl [, b], then the integrl of f(x) over [, b] is the re under f over the
Line Integrls The ide of line integrl is very similr to tht of single integrls. If the function f(x) is bove the x-xis on the intervl [, b], then the integrl of f(x) over [, b] is the re under f over the
such that the S i cover S, or equivalently S
 MATH 55 Triple Integrls Fll 16 1. Definition Given solid in spce, prtition of consists of finite set of solis = { 1,, n } such tht the i cover, or equivlently n i. Furthermore, for ech i, intersects i
MATH 55 Triple Integrls Fll 16 1. Definition Given solid in spce, prtition of consists of finite set of solis = { 1,, n } such tht the i cover, or equivlently n i. Furthermore, for ech i, intersects i
Section 10.4 Hyperbolas
 66 Section 10.4 Hyperbols Objective : Definition of hyperbol & hyperbols centered t (0, 0). The third type of conic we will study is the hyperbol. It is defined in the sme mnner tht we defined the prbol
66 Section 10.4 Hyperbols Objective : Definition of hyperbol & hyperbols centered t (0, 0). The third type of conic we will study is the hyperbol. It is defined in the sme mnner tht we defined the prbol
MATH 2530: WORKSHEET 7. x 2 y dz dy dx =
 MATH 253: WORKSHT 7 () Wrm-up: () Review: polr coordintes, integrls involving polr coordintes, triple Riemnn sums, triple integrls, the pplictions of triple integrls (especilly to volume), nd cylindricl
MATH 253: WORKSHT 7 () Wrm-up: () Review: polr coordintes, integrls involving polr coordintes, triple Riemnn sums, triple integrls, the pplictions of triple integrls (especilly to volume), nd cylindricl
Iterated Integrals. f (x; y) dy dx. p(x) To evaluate a type I integral, we rst evaluate the inner integral Z q(x) f (x; y) dy.
 Iterted Integrls Type I Integrls In this section, we begin the study of integrls over regions in the plne. To do so, however, requires tht we exmine the importnt ide of iterted integrls, in which inde
Iterted Integrls Type I Integrls In this section, we begin the study of integrls over regions in the plne. To do so, however, requires tht we exmine the importnt ide of iterted integrls, in which inde
Stained Glass Design. Teaching Goals:
 Stined Glss Design Time required 45-90 minutes Teching Gols: 1. Students pply grphic methods to design vrious shpes on the plne.. Students pply geometric trnsformtions of grphs of functions in order to
Stined Glss Design Time required 45-90 minutes Teching Gols: 1. Students pply grphic methods to design vrious shpes on the plne.. Students pply geometric trnsformtions of grphs of functions in order to
Unit #9 : Definite Integral Properties, Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties, Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties, Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Area & Volume. Chapter 6.1 & 6.2 September 25, y = 1! x 2. Back to Area:
 Bck to Are: Are & Volume Chpter 6. & 6. Septemer 5, 6 We cn clculte the re etween the x-xis nd continuous function f on the intervl [,] using the definite integrl:! f x = lim$ f x * i )%x n i= Where fx
Bck to Are: Are & Volume Chpter 6. & 6. Septemer 5, 6 We cn clculte the re etween the x-xis nd continuous function f on the intervl [,] using the definite integrl:! f x = lim$ f x * i )%x n i= Where fx
9.1 apply the distance and midpoint formulas
 9.1 pply the distnce nd midpoint formuls DISTANCE FORMULA MIDPOINT FORMULA To find the midpoint between two points x, y nd x y 1 1,, we Exmple 1: Find the distnce between the two points. Then, find the
9.1 pply the distnce nd midpoint formuls DISTANCE FORMULA MIDPOINT FORMULA To find the midpoint between two points x, y nd x y 1 1,, we Exmple 1: Find the distnce between the two points. Then, find the
Math 464 Fall 2012 Notes on Marginal and Conditional Densities October 18, 2012
 Mth 464 Fll 2012 Notes on Mrginl nd Conditionl Densities klin@mth.rizon.edu October 18, 2012 Mrginl densities. Suppose you hve 3 continuous rndom vribles X, Y, nd Z, with joint density f(x,y,z. The mrginl
Mth 464 Fll 2012 Notes on Mrginl nd Conditionl Densities klin@mth.rizon.edu October 18, 2012 Mrginl densities. Suppose you hve 3 continuous rndom vribles X, Y, nd Z, with joint density f(x,y,z. The mrginl
Integration. October 25, 2016
 Integrtion October 5, 6 Introduction We hve lerned in previous chpter on how to do the differentition. It is conventionl in mthemtics tht we re supposed to lern bout the integrtion s well. As you my hve
Integrtion October 5, 6 Introduction We hve lerned in previous chpter on how to do the differentition. It is conventionl in mthemtics tht we re supposed to lern bout the integrtion s well. As you my hve
Applications of the Definite Integral ( Areas and Volumes)
 Mth1242 Project II Nme: Applictions of the Definite Integrl ( Ares nd Volumes) In this project, we explore some pplictions of the definite integrl. We use integrls to find the re etween the grphs of two
Mth1242 Project II Nme: Applictions of the Definite Integrl ( Ares nd Volumes) In this project, we explore some pplictions of the definite integrl. We use integrls to find the re etween the grphs of two
Math 142, Exam 1 Information.
 Mth 14, Exm 1 Informtion. 9/14/10, LC 41, 9:30-10:45. Exm 1 will be bsed on: Sections 7.1-7.5. The corresponding ssigned homework problems (see http://www.mth.sc.edu/ boyln/sccourses/14f10/14.html) At
Mth 14, Exm 1 Informtion. 9/14/10, LC 41, 9:30-10:45. Exm 1 will be bsed on: Sections 7.1-7.5. The corresponding ssigned homework problems (see http://www.mth.sc.edu/ boyln/sccourses/14f10/14.html) At
Integration. September 28, 2017
 Integrtion September 8, 7 Introduction We hve lerned in previous chpter on how to do the differentition. It is conventionl in mthemtics tht we re supposed to lern bout the integrtion s well. As you my
Integrtion September 8, 7 Introduction We hve lerned in previous chpter on how to do the differentition. It is conventionl in mthemtics tht we re supposed to lern bout the integrtion s well. As you my
Yoplait with Areas and Volumes
 Yoplit with Ares nd Volumes Yoplit yogurt comes in two differently shped continers. One is truncted cone nd the other is n ellipticl cylinder (see photos below). In this exercise, you will determine the
Yoplit with Ares nd Volumes Yoplit yogurt comes in two differently shped continers. One is truncted cone nd the other is n ellipticl cylinder (see photos below). In this exercise, you will determine the
8.2 Areas in the Plane
 39 Chpter 8 Applictions of Definite Integrls 8. Ares in the Plne Wht ou will lern out... Are Between Curves Are Enclosed Intersecting Curves Boundries with Chnging Functions Integrting with Respect to
39 Chpter 8 Applictions of Definite Integrls 8. Ares in the Plne Wht ou will lern out... Are Between Curves Are Enclosed Intersecting Curves Boundries with Chnging Functions Integrting with Respect to
50 AMC LECTURES Lecture 2 Analytic Geometry Distance and Lines. can be calculated by the following formula:
 5 AMC LECTURES Lecture Anlytic Geometry Distnce nd Lines BASIC KNOWLEDGE. Distnce formul The distnce (d) between two points P ( x, y) nd P ( x, y) cn be clculted by the following formul: d ( x y () x )
5 AMC LECTURES Lecture Anlytic Geometry Distnce nd Lines BASIC KNOWLEDGE. Distnce formul The distnce (d) between two points P ( x, y) nd P ( x, y) cn be clculted by the following formul: d ( x y () x )
1 Quad-Edge Construction Operators
 CS48: Computer Grphics Hndout # Geometric Modeling Originl Hndout #5 Stnford University Tuesdy, 8 December 99 Originl Lecture #5: 9 November 99 Topics: Mnipultions with Qud-Edge Dt Structures Scribe: Mike
CS48: Computer Grphics Hndout # Geometric Modeling Originl Hndout #5 Stnford University Tuesdy, 8 December 99 Originl Lecture #5: 9 November 99 Topics: Mnipultions with Qud-Edge Dt Structures Scribe: Mike
Solutions to Math 41 Final Exam December 12, 2011
 Solutions to Mth Finl Em December,. ( points) Find ech of the following its, with justifiction. If there is n infinite it, then eplin whether it is or. ( ) / ln() () (5 points) First we compute the it:
Solutions to Mth Finl Em December,. ( points) Find ech of the following its, with justifiction. If there is n infinite it, then eplin whether it is or. ( ) / ln() () (5 points) First we compute the it:
Class-XI Mathematics Conic Sections Chapter-11 Chapter Notes Key Concepts
 Clss-XI Mthemtics Conic Sections Chpter-11 Chpter Notes Key Concepts 1. Let be fixed verticl line nd m be nother line intersecting it t fixed point V nd inclined to it t nd ngle On rotting the line m round
Clss-XI Mthemtics Conic Sections Chpter-11 Chpter Notes Key Concepts 1. Let be fixed verticl line nd m be nother line intersecting it t fixed point V nd inclined to it t nd ngle On rotting the line m round
Pythagoras theorem and trigonometry (2)
 HPTR 10 Pythgors theorem nd trigonometry (2) 31 HPTR Liner equtions In hpter 19, Pythgors theorem nd trigonometry were used to find the lengths of sides nd the sizes of ngles in right-ngled tringles. These
HPTR 10 Pythgors theorem nd trigonometry (2) 31 HPTR Liner equtions In hpter 19, Pythgors theorem nd trigonometry were used to find the lengths of sides nd the sizes of ngles in right-ngled tringles. These
2 Computing all Intersections of a Set of Segments Line Segment Intersection
 15-451/651: Design & Anlysis of Algorithms Novemer 14, 2016 Lecture #21 Sweep-Line nd Segment Intersection lst chnged: Novemer 8, 2017 1 Preliminries The sweep-line prdigm is very powerful lgorithmic design
15-451/651: Design & Anlysis of Algorithms Novemer 14, 2016 Lecture #21 Sweep-Line nd Segment Intersection lst chnged: Novemer 8, 2017 1 Preliminries The sweep-line prdigm is very powerful lgorithmic design
MA 124 (Calculus II) Lecture 2: January 24, 2019 Section A3. Professor Jennifer Balakrishnan,
 Wht is on tody Professor Jennifer Blkrishnn, jbl@bu.edu 1 Velocity nd net chnge 1 2 Regions between curves 3 1 Velocity nd net chnge Briggs-Cochrn-Gillett 6.1 pp. 398-46 Suppose you re driving long stright
Wht is on tody Professor Jennifer Blkrishnn, jbl@bu.edu 1 Velocity nd net chnge 1 2 Regions between curves 3 1 Velocity nd net chnge Briggs-Cochrn-Gillett 6.1 pp. 398-46 Suppose you re driving long stright
arxiv: v2 [math.ho] 4 Jun 2012
![arxiv: v2 [math.ho] 4 Jun 2012 arxiv: v2 [math.ho] 4 Jun 2012](/thumbs/76/73512534.jpg) Volumes of olids of Revolution. Unified pproch Jorge Mrtín-Morles nd ntonio M. Oller-Mrcén jorge@unizr.es, oller@unizr.es rxiv:5.v [mth.ho] Jun Centro Universitrio de l Defens - IUM. cdemi Generl Militr,
Volumes of olids of Revolution. Unified pproch Jorge Mrtín-Morles nd ntonio M. Oller-Mrcén jorge@unizr.es, oller@unizr.es rxiv:5.v [mth.ho] Jun Centro Universitrio de l Defens - IUM. cdemi Generl Militr,
Introduction to Integration
 Introduction to Integrtion Definite integrls of piecewise constnt functions A constnt function is function of the form Integrtion is two things t the sme time: A form of summtion. The opposite of differentition.
Introduction to Integrtion Definite integrls of piecewise constnt functions A constnt function is function of the form Integrtion is two things t the sme time: A form of summtion. The opposite of differentition.
Improper Integrals. October 4, 2017
 Improper Integrls October 4, 7 Introduction We hve seen how to clculte definite integrl when the it is rel number. However, there re times when we re interested to compute the integrl sy for emple 3. Here
Improper Integrls October 4, 7 Introduction We hve seen how to clculte definite integrl when the it is rel number. However, there re times when we re interested to compute the integrl sy for emple 3. Here
Ray surface intersections
 Ry surfce intersections Some primitives Finite primitives: polygons spheres, cylinders, cones prts of generl qudrics Infinite primitives: plnes infinite cylinders nd cones generl qudrics A finite primitive
Ry surfce intersections Some primitives Finite primitives: polygons spheres, cylinders, cones prts of generl qudrics Infinite primitives: plnes infinite cylinders nd cones generl qudrics A finite primitive
INTRODUCTION TO SIMPLICIAL COMPLEXES
 INTRODUCTION TO SIMPLICIAL COMPLEXES CASEY KELLEHER AND ALESSANDRA PANTANO 0.1. Introduction. In this ctivity set we re going to introduce notion from Algebric Topology clled simplicil homology. The min
INTRODUCTION TO SIMPLICIAL COMPLEXES CASEY KELLEHER AND ALESSANDRA PANTANO 0.1. Introduction. In this ctivity set we re going to introduce notion from Algebric Topology clled simplicil homology. The min
Introduction Transformation formulae Polar graphs Standard curves Polar equations Test GRAPHS INU0114/514 (MATHS 1)
 POLAR EQUATIONS AND GRAPHS GEOMETRY INU4/54 (MATHS ) Dr Adrin Jnnett MIMA CMth FRAS Polr equtions nd grphs / 6 Adrin Jnnett Objectives The purpose of this presenttion is to cover the following topics:
POLAR EQUATIONS AND GRAPHS GEOMETRY INU4/54 (MATHS ) Dr Adrin Jnnett MIMA CMth FRAS Polr equtions nd grphs / 6 Adrin Jnnett Objectives The purpose of this presenttion is to cover the following topics:
MTH 146 Conics Supplement
 105- Review of Conics MTH 146 Conics Supplement In this section we review conics If ou ne more detils thn re present in the notes, r through section 105 of the ook Definition: A prol is the set of points
105- Review of Conics MTH 146 Conics Supplement In this section we review conics If ou ne more detils thn re present in the notes, r through section 105 of the ook Definition: A prol is the set of points
Grade 7/8 Math Circles Geometric Arithmetic October 31, 2012
 Fculty of Mthemtics Wterloo, Ontrio N2L 3G1 Grde 7/8 Mth Circles Geometric Arithmetic Octoer 31, 2012 Centre for Eduction in Mthemtics nd Computing Ancient Greece hs given irth to some of the most importnt
Fculty of Mthemtics Wterloo, Ontrio N2L 3G1 Grde 7/8 Mth Circles Geometric Arithmetic Octoer 31, 2012 Centre for Eduction in Mthemtics nd Computing Ancient Greece hs given irth to some of the most importnt
Section 3.1: Sequences and Series
 Section.: Sequences d Series Sequences Let s strt out with the definition of sequence: sequence: ordered list of numbers, often with definite pttern Recll tht in set, order doesn t mtter so this is one
Section.: Sequences d Series Sequences Let s strt out with the definition of sequence: sequence: ordered list of numbers, often with definite pttern Recll tht in set, order doesn t mtter so this is one
Math 35 Review Sheet, Spring 2014
 Mth 35 Review heet, pring 2014 For the finl exm, do ny 12 of the 15 questions in 3 hours. They re worth 8 points ech, mking 96, with 4 more points for netness! Put ll your work nd nswers in the provided
Mth 35 Review heet, pring 2014 For the finl exm, do ny 12 of the 15 questions in 3 hours. They re worth 8 points ech, mking 96, with 4 more points for netness! Put ll your work nd nswers in the provided
1 Drawing 3D Objects in Adobe Illustrator
 Drwing 3D Objects in Adobe Illustrtor 1 1 Drwing 3D Objects in Adobe Illustrtor This Tutoril will show you how to drw simple objects with three-dimensionl ppernce. At first we will drw rrows indicting
Drwing 3D Objects in Adobe Illustrtor 1 1 Drwing 3D Objects in Adobe Illustrtor This Tutoril will show you how to drw simple objects with three-dimensionl ppernce. At first we will drw rrows indicting
10.5 Graphing Quadratic Functions
 0.5 Grphing Qudrtic Functions Now tht we cn solve qudrtic equtions, we wnt to lern how to grph the function ssocited with the qudrtic eqution. We cll this the qudrtic function. Grphs of Qudrtic Functions
0.5 Grphing Qudrtic Functions Now tht we cn solve qudrtic equtions, we wnt to lern how to grph the function ssocited with the qudrtic eqution. We cll this the qudrtic function. Grphs of Qudrtic Functions
9 4. CISC - Curriculum & Instruction Steering Committee. California County Superintendents Educational Services Association
 9. CISC - Curriculum & Instruction Steering Committee The Winning EQUATION A HIGH QUALITY MATHEMATICS PROFESSIONAL DEVELOPMENT PROGRAM FOR TEACHERS IN GRADES THROUGH ALGEBRA II STRAND: NUMBER SENSE: Rtionl
9. CISC - Curriculum & Instruction Steering Committee The Winning EQUATION A HIGH QUALITY MATHEMATICS PROFESSIONAL DEVELOPMENT PROGRAM FOR TEACHERS IN GRADES THROUGH ALGEBRA II STRAND: NUMBER SENSE: Rtionl
Pointwise convergence need not behave well with respect to standard properties such as continuity.
 Chpter 3 Uniform Convergence Lecture 9 Sequences of functions re of gret importnce in mny res of pure nd pplied mthemtics, nd their properties cn often be studied in the context of metric spces, s in Exmples
Chpter 3 Uniform Convergence Lecture 9 Sequences of functions re of gret importnce in mny res of pure nd pplied mthemtics, nd their properties cn often be studied in the context of metric spces, s in Exmples
APPLICATIONS OF INTEGRATION
 Chpter 3 DACS 1 Lok 004/05 CHAPTER 5 APPLICATIONS OF INTEGRATION 5.1 Geometricl Interprettion-Definite Integrl (pge 36) 5. Are of Region (pge 369) 5..1 Are of Region Under Grph (pge 369) Figure 5.7 shows
Chpter 3 DACS 1 Lok 004/05 CHAPTER 5 APPLICATIONS OF INTEGRATION 5.1 Geometricl Interprettion-Definite Integrl (pge 36) 5. Are of Region (pge 369) 5..1 Are of Region Under Grph (pge 369) Figure 5.7 shows
Answer Key Lesson 6: Workshop: Angles and Lines
 nswer Key esson 6: tudent Guide ngles nd ines Questions 1 3 (G p. 406) 1. 120 ; 360 2. hey re the sme. 3. 360 Here re four different ptterns tht re used to mke quilts. Work with your group. se your Power
nswer Key esson 6: tudent Guide ngles nd ines Questions 1 3 (G p. 406) 1. 120 ; 360 2. hey re the sme. 3. 360 Here re four different ptterns tht re used to mke quilts. Work with your group. se your Power
Hyperbolas. Definition of Hyperbola
 CHAT Pre-Clculus Hyperols The third type of conic is clled hyperol. For n ellipse, the sum of the distnces from the foci nd point on the ellipse is fixed numer. For hyperol, the difference of the distnces
CHAT Pre-Clculus Hyperols The third type of conic is clled hyperol. For n ellipse, the sum of the distnces from the foci nd point on the ellipse is fixed numer. For hyperol, the difference of the distnces
Graphing Conic Sections
 Grphing Conic Sections Definition of Circle Set of ll points in plne tht re n equl distnce, clled the rdius, from fixed point in tht plne, clled the center. Grphing Circle (x h) 2 + (y k) 2 = r 2 where
Grphing Conic Sections Definition of Circle Set of ll points in plne tht re n equl distnce, clled the rdius, from fixed point in tht plne, clled the center. Grphing Circle (x h) 2 + (y k) 2 = r 2 where
Topics in Analytic Geometry
 Nme Chpter 10 Topics in Anltic Geometr Section 10.1 Lines Objective: In this lesson ou lerned how to find the inclintion of line, the ngle between two lines, nd the distnce between point nd line. Importnt
Nme Chpter 10 Topics in Anltic Geometr Section 10.1 Lines Objective: In this lesson ou lerned how to find the inclintion of line, the ngle between two lines, nd the distnce between point nd line. Importnt
Unit 5 Vocabulary. A function is a special relationship where each input has a single output.
 MODULE 3 Terms Definition Picture/Exmple/Nottion 1 Function Nottion Function nottion is n efficient nd effective wy to write functions of ll types. This nottion llows you to identify the input vlue with
MODULE 3 Terms Definition Picture/Exmple/Nottion 1 Function Nottion Function nottion is n efficient nd effective wy to write functions of ll types. This nottion llows you to identify the input vlue with
)
 Chpter Five /SOLUTIONS Since the speed ws between nd mph during this five minute period, the fuel efficienc during this period is between 5 mpg nd 8 mpg. So the fuel used during this period is between
Chpter Five /SOLUTIONS Since the speed ws between nd mph during this five minute period, the fuel efficienc during this period is between 5 mpg nd 8 mpg. So the fuel used during this period is between
The Basic Properties of the Integral
 The Bsic Properties of the Integrl When we compute the derivtive of complicted function, like + sin, we usull use differentition rules, like d [f()+g()] d f()+ d g(), to reduce the computtion d d d to
The Bsic Properties of the Integrl When we compute the derivtive of complicted function, like + sin, we usull use differentition rules, like d [f()+g()] d f()+ d g(), to reduce the computtion d d d to
Angle Properties in Polygons. Part 1 Interior Angles
 2.4 Angle Properties in Polygons YOU WILL NEED dynmic geometry softwre OR protrctor nd ruler EXPLORE A pentgon hs three right ngles nd four sides of equl length, s shown. Wht is the sum of the mesures
2.4 Angle Properties in Polygons YOU WILL NEED dynmic geometry softwre OR protrctor nd ruler EXPLORE A pentgon hs three right ngles nd four sides of equl length, s shown. Wht is the sum of the mesures
Subtracting Fractions
 Lerning Enhncement Tem Model Answers: Adding nd Subtrcting Frctions Adding nd Subtrcting Frctions study guide. When the frctions both hve the sme denomintor (bottom) you cn do them using just simple dding
Lerning Enhncement Tem Model Answers: Adding nd Subtrcting Frctions Adding nd Subtrcting Frctions study guide. When the frctions both hve the sme denomintor (bottom) you cn do them using just simple dding
Geometric transformations
 Geometric trnsformtions Computer Grphics Some slides re bsed on Shy Shlom slides from TAU mn n n m m T A,,,,,, 2 1 2 22 12 1 21 11 Rows become columns nd columns become rows nm n n m m A,,,,,, 1 1 2 22
Geometric trnsformtions Computer Grphics Some slides re bsed on Shy Shlom slides from TAU mn n n m m T A,,,,,, 2 1 2 22 12 1 21 11 Rows become columns nd columns become rows nm n n m m A,,,,,, 1 1 2 22
Fig.1. Let a source of monochromatic light be incident on a slit of finite width a, as shown in Fig. 1.
 Answer on Question #5692, Physics, Optics Stte slient fetures of single slit Frunhofer diffrction pttern. The slit is verticl nd illuminted by point source. Also, obtin n expression for intensity distribution
Answer on Question #5692, Physics, Optics Stte slient fetures of single slit Frunhofer diffrction pttern. The slit is verticl nd illuminted by point source. Also, obtin n expression for intensity distribution
MA1008. Calculus and Linear Algebra for Engineers. Course Notes for Section B. Stephen Wills. Department of Mathematics. University College Cork
 MA1008 Clculus nd Liner Algebr for Engineers Course Notes for Section B Stephen Wills Deprtment of Mthemtics University College Cork s.wills@ucc.ie http://euclid.ucc.ie/pges/stff/wills/teching/m1008/ma1008.html
MA1008 Clculus nd Liner Algebr for Engineers Course Notes for Section B Stephen Wills Deprtment of Mthemtics University College Cork s.wills@ucc.ie http://euclid.ucc.ie/pges/stff/wills/teching/m1008/ma1008.html
MATH 25 CLASS 5 NOTES, SEP
 MATH 25 CLASS 5 NOTES, SEP 30 2011 Contents 1. A brief diversion: reltively prime numbers 1 2. Lest common multiples 3 3. Finding ll solutions to x + by = c 4 Quick links to definitions/theorems Euclid
MATH 25 CLASS 5 NOTES, SEP 30 2011 Contents 1. A brief diversion: reltively prime numbers 1 2. Lest common multiples 3 3. Finding ll solutions to x + by = c 4 Quick links to definitions/theorems Euclid
1. SEQUENCES INVOLVING EXPONENTIAL GROWTH (GEOMETRIC SEQUENCES)
 Numbers nd Opertions, Algebr, nd Functions 45. SEQUENCES INVOLVING EXPONENTIAL GROWTH (GEOMETRIC SEQUENCES) In sequence of terms involving eponentil growth, which the testing service lso clls geometric
Numbers nd Opertions, Algebr, nd Functions 45. SEQUENCES INVOLVING EXPONENTIAL GROWTH (GEOMETRIC SEQUENCES) In sequence of terms involving eponentil growth, which the testing service lso clls geometric
f[a] x + f[a + x] x + f[a +2 x] x + + f[b x] x
![f[a] x + f[a + x] x + f[a +2 x] x + + f[b x] x f[a] x + f[a + x] x + f[a +2 x] x + + f[b x] x](/thumbs/81/84236407.jpg) Bsic Integrtion This chpter contins the fundmentl theory of integrtion. We begin with some problems to motivte the min ide: pproximtion by sum of slices. The chpter confronts this squrely, nd Chpter 3
Bsic Integrtion This chpter contins the fundmentl theory of integrtion. We begin with some problems to motivte the min ide: pproximtion by sum of slices. The chpter confronts this squrely, nd Chpter 3
Essential Question What are some of the characteristics of the graph of a rational function?
 8. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..G A..H A..K Grphing Rtionl Functions Essentil Question Wht re some of the chrcteristics of the grph of rtionl function? The prent function for rtionl functions
8. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS A..A A..G A..H A..K Grphing Rtionl Functions Essentil Question Wht re some of the chrcteristics of the grph of rtionl function? The prent function for rtionl functions
Double Integrals. MATH 375 Numerical Analysis. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan Double Integrals
 Double Integrls MATH 375 Numericl Anlysis J. Robert Buchnn Deprtment of Mthemtics Fll 2013 J. Robert Buchnn Double Integrls Objectives Now tht we hve discussed severl methods for pproximting definite integrls
Double Integrls MATH 375 Numericl Anlysis J. Robert Buchnn Deprtment of Mthemtics Fll 2013 J. Robert Buchnn Double Integrls Objectives Now tht we hve discussed severl methods for pproximting definite integrls
The Fundamental Theorem of Calculus
 MATH 6 The Fundmentl Theorem of Clculus The Fundmentl Theorem of Clculus (FTC) gives method of finding the signed re etween the grph of f nd the x-xis on the intervl [, ]. The theorem is: FTC: If f is
MATH 6 The Fundmentl Theorem of Clculus The Fundmentl Theorem of Clculus (FTC) gives method of finding the signed re etween the grph of f nd the x-xis on the intervl [, ]. The theorem is: FTC: If f is
12-B FRACTIONS AND DECIMALS
 -B Frctions nd Decimls. () If ll four integers were negtive, their product would be positive, nd so could not equl one of them. If ll four integers were positive, their product would be much greter thn
-B Frctions nd Decimls. () If ll four integers were negtive, their product would be positive, nd so could not equl one of them. If ll four integers were positive, their product would be much greter thn
Supplemental Notes: Line Integrals
 Nottion: Supplementl Notes: Line Integrls Let be n oriented curve prmeterized by r(t) = x(t), y(t), z(t) where t b. denotes the curve with its orienttion reversed. 1 + 2 mens tke curve 1 nd curve 2 nd
Nottion: Supplementl Notes: Line Integrls Let be n oriented curve prmeterized by r(t) = x(t), y(t), z(t) where t b. denotes the curve with its orienttion reversed. 1 + 2 mens tke curve 1 nd curve 2 nd
Conic Sections Parabola Objective: Define conic section, parabola, draw a parabola, standard equations and their graphs
 Conic Sections Prol Ojective: Define conic section, prol, drw prol, stndrd equtions nd their grphs The curves creted y intersecting doule npped right circulr cone with plne re clled conic sections. If
Conic Sections Prol Ojective: Define conic section, prol, drw prol, stndrd equtions nd their grphs The curves creted y intersecting doule npped right circulr cone with plne re clled conic sections. If
Matlab s Numerical Integration Commands
 Mtlb s Numericl Integrtion Commnds The relevnt commnds we consider re qud nd dblqud, triplequd. See the Mtlb help files for other integrtion commnds. By the wy, qud refers to dptive qudrture. To integrte:
Mtlb s Numericl Integrtion Commnds The relevnt commnds we consider re qud nd dblqud, triplequd. See the Mtlb help files for other integrtion commnds. By the wy, qud refers to dptive qudrture. To integrte:
Midterm 2 Sample solution
 Nme: Instructions Midterm 2 Smple solution CMSC 430 Introduction to Compilers Fll 2012 November 28, 2012 This exm contins 9 pges, including this one. Mke sure you hve ll the pges. Write your nme on the
Nme: Instructions Midterm 2 Smple solution CMSC 430 Introduction to Compilers Fll 2012 November 28, 2012 This exm contins 9 pges, including this one. Mke sure you hve ll the pges. Write your nme on the
Introduction. Chapter 4: Complex Integration. Introduction (Cont d)
 Introduction Chpter 4: Complex Integrtion Li, Yongzho Stte Key Lbortory of Integrted Services Networks, Xidin University October 10, 2010 The two-dimensionl nture of the complex plne required us to generlize
Introduction Chpter 4: Complex Integrtion Li, Yongzho Stte Key Lbortory of Integrted Services Networks, Xidin University October 10, 2010 The two-dimensionl nture of the complex plne required us to generlize
6.3 Definite Integrals and Antiderivatives
 Section 6. Definite Integrls nd Antiderivtives 8 6. Definite Integrls nd Antiderivtives Wht ou will lern out... Properties of Definite Integrls Averge Vlue of Function Men Vlue Theorem for Definite Integrls
Section 6. Definite Integrls nd Antiderivtives 8 6. Definite Integrls nd Antiderivtives Wht ou will lern out... Properties of Definite Integrls Averge Vlue of Function Men Vlue Theorem for Definite Integrls
3.5.1 Single slit diffraction
 3.5.1 Single slit diffrction Wves pssing through single slit will lso diffrct nd produce n interference pttern. The reson for this is to do with the finite width of the slit. We will consider this lter.
3.5.1 Single slit diffrction Wves pssing through single slit will lso diffrct nd produce n interference pttern. The reson for this is to do with the finite width of the slit. We will consider this lter.
Date: 9.1. Conics: Parabolas
 Dte: 9. Conics: Prols Preclculus H. Notes: Unit 9 Conics Conic Sections: curves tht re formed y the intersection of plne nd doulenpped cone Syllus Ojectives:. The student will grph reltions or functions,
Dte: 9. Conics: Prols Preclculus H. Notes: Unit 9 Conics Conic Sections: curves tht re formed y the intersection of plne nd doulenpped cone Syllus Ojectives:. The student will grph reltions or functions,
4452 Mathematical Modeling Lecture 4: Lagrange Multipliers
 Mth Modeling Lecture 4: Lgrnge Multipliers Pge 4452 Mthemticl Modeling Lecture 4: Lgrnge Multipliers Lgrnge multipliers re high powered mthemticl technique to find the mximum nd minimum of multidimensionl
Mth Modeling Lecture 4: Lgrnge Multipliers Pge 4452 Mthemticl Modeling Lecture 4: Lgrnge Multipliers Lgrnge multipliers re high powered mthemticl technique to find the mximum nd minimum of multidimensionl
3.5.1 Single slit diffraction
 3..1 Single slit diffrction ves pssing through single slit will lso diffrct nd produce n interference pttern. The reson for this is to do with the finite width of the slit. e will consider this lter. Tke
3..1 Single slit diffrction ves pssing through single slit will lso diffrct nd produce n interference pttern. The reson for this is to do with the finite width of the slit. e will consider this lter. Tke
Chapter44. Polygons and solids. Contents: A Polygons B Triangles C Quadrilaterals D Solids E Constructing solids
 Chpter44 Polygons nd solids Contents: A Polygons B Tringles C Qudrilterls D Solids E Constructing solids 74 POLYGONS AND SOLIDS (Chpter 4) Opening prolem Things to think out: c Wht different shpes cn you
Chpter44 Polygons nd solids Contents: A Polygons B Tringles C Qudrilterls D Solids E Constructing solids 74 POLYGONS AND SOLIDS (Chpter 4) Opening prolem Things to think out: c Wht different shpes cn you
In the last lecture, we discussed how valid tokens may be specified by regular expressions.
 LECTURE 5 Scnning SYNTAX ANALYSIS We know from our previous lectures tht the process of verifying the syntx of the progrm is performed in two stges: Scnning: Identifying nd verifying tokens in progrm.
LECTURE 5 Scnning SYNTAX ANALYSIS We know from our previous lectures tht the process of verifying the syntx of the progrm is performed in two stges: Scnning: Identifying nd verifying tokens in progrm.
x )Scales are the reciprocal of each other. e
 9. Reciprocls A Complete Slide Rule Mnul - eville W Young Chpter 9 Further Applictions of the LL scles The LL (e x ) scles nd the corresponding LL 0 (e -x or Exmple : 0.244 4.. Set the hir line over 4.
9. Reciprocls A Complete Slide Rule Mnul - eville W Young Chpter 9 Further Applictions of the LL scles The LL (e x ) scles nd the corresponding LL 0 (e -x or Exmple : 0.244 4.. Set the hir line over 4.
P(r)dr = probability of generating a random number in the interval dr near r. For this probability idea to make sense we must have
 Rndom Numers nd Monte Crlo Methods Rndom Numer Methods The integrtion methods discussed so fr ll re sed upon mking polynomil pproximtions to the integrnd. Another clss of numericl methods relies upon using
Rndom Numers nd Monte Crlo Methods Rndom Numer Methods The integrtion methods discussed so fr ll re sed upon mking polynomil pproximtions to the integrnd. Another clss of numericl methods relies upon using
6.4: SHELL METHOD 6.5: WORK AND ENERGY NAME: SOLUTIONS Math 1910 September 26, 2017
 6.4: SHELL METHOD 6.5: WORK AND ENERGY NAME: SOLUTIONS Mt 9 September 26, 27 ONE-PAGE REVIEW Sell Metod: Wen you rotte te region between two grps round n xis, te segments prllel to te xis generte cylindricl
6.4: SHELL METHOD 6.5: WORK AND ENERGY NAME: SOLUTIONS Mt 9 September 26, 27 ONE-PAGE REVIEW Sell Metod: Wen you rotte te region between two grps round n xis, te segments prllel to te xis generte cylindricl
1 The Definite Integral
 The Definite Integrl Definition. Let f be function defined on the intervl [, b] where
The Definite Integrl Definition. Let f be function defined on the intervl [, b] where
5/9/17. Lesson 51 - FTC PART 2. Review FTC, PART 1. statement as the Integral Evaluation Theorem as it tells us HOW to evaluate the definite integral
 Lesson - FTC PART 2 Review! We hve seen definition/formul for definite integrl s n b A() = lim f ( i )Δ = f ()d = F() = F(b) F() n i=! where F () = f() (or F() is the ntiderivtive of f() b! And hve seen
Lesson - FTC PART 2 Review! We hve seen definition/formul for definite integrl s n b A() = lim f ( i )Δ = f ()d = F() = F(b) F() n i=! where F () = f() (or F() is the ntiderivtive of f() b! And hve seen
Representation of Numbers. Number Representation. Representation of Numbers. 32-bit Unsigned Integers 3/24/2014. Fixed point Integer Representation
 Representtion of Numbers Number Representtion Computer represent ll numbers, other thn integers nd some frctions with imprecision. Numbers re stored in some pproximtion which cn be represented by fixed
Representtion of Numbers Number Representtion Computer represent ll numbers, other thn integers nd some frctions with imprecision. Numbers re stored in some pproximtion which cn be represented by fixed
Lecture 7: Integration Techniques
 Lecture 7: Integrtion Techniques Antiderivtives nd Indefinite Integrls. In differentil clculus, we were interested in the derivtive of given rel-vlued function, whether it ws lgeric, eponentil or logrithmic.
Lecture 7: Integrtion Techniques Antiderivtives nd Indefinite Integrls. In differentil clculus, we were interested in the derivtive of given rel-vlued function, whether it ws lgeric, eponentil or logrithmic.
HW Stereotactic Targeting
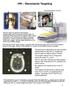 HW Stereotctic Trgeting We re bout to perform stereotctic rdiosurgery with the Gmm Knife under CT guidnce. We instrument the ptient with bse ring nd for CT scnning we ttch fiducil cge (FC). Above: bse
HW Stereotctic Trgeting We re bout to perform stereotctic rdiosurgery with the Gmm Knife under CT guidnce. We instrument the ptient with bse ring nd for CT scnning we ttch fiducil cge (FC). Above: bse
Math Line Integrals I
 Mth 213 - Line Integrls I Peter A. Perry University of Kentucky November 16, 2018 Homework Re-Red Section 16.2 for Mondy Work on Stewrt problems for 16.2: 1-21 (odd), 33-41 (odd), 49, 50 Begin Webwork
Mth 213 - Line Integrls I Peter A. Perry University of Kentucky November 16, 2018 Homework Re-Red Section 16.2 for Mondy Work on Stewrt problems for 16.2: 1-21 (odd), 33-41 (odd), 49, 50 Begin Webwork
TASK SPECIFIC DESCRIPTION
 MYP Algebr II/Trig Unit 2 Ch. 4 Trnsformtions Project Nme: Block: - Due Dte: Tuesdy, 11/7 (B-dy) & Wednesdy, 11/8 (A-dy) Mterils: Grph pper, ruler, protrctor, compss, highlight mrkers/colored pencils SCORE:
MYP Algebr II/Trig Unit 2 Ch. 4 Trnsformtions Project Nme: Block: - Due Dte: Tuesdy, 11/7 (B-dy) & Wednesdy, 11/8 (A-dy) Mterils: Grph pper, ruler, protrctor, compss, highlight mrkers/colored pencils SCORE:
ECE 468/573 Midterm 1 September 28, 2012
 ECE 468/573 Midterm 1 September 28, 2012 Nme:! Purdue emil:! Plese sign the following: I ffirm tht the nswers given on this test re mine nd mine lone. I did not receive help from ny person or mteril (other
ECE 468/573 Midterm 1 September 28, 2012 Nme:! Purdue emil:! Plese sign the following: I ffirm tht the nswers given on this test re mine nd mine lone. I did not receive help from ny person or mteril (other
CS311H: Discrete Mathematics. Graph Theory IV. A Non-planar Graph. Regions of a Planar Graph. Euler s Formula. Instructor: Işıl Dillig
 CS311H: Discrete Mthemtics Grph Theory IV Instructor: Işıl Dillig Instructor: Işıl Dillig, CS311H: Discrete Mthemtics Grph Theory IV 1/25 A Non-plnr Grph Regions of Plnr Grph The plnr representtion of
CS311H: Discrete Mthemtics Grph Theory IV Instructor: Işıl Dillig Instructor: Işıl Dillig, CS311H: Discrete Mthemtics Grph Theory IV 1/25 A Non-plnr Grph Regions of Plnr Grph The plnr representtion of
9 Graph Cutting Procedures
 9 Grph Cutting Procedures Lst clss we begn looking t how to embed rbitrry metrics into distributions of trees, nd proved the following theorem due to Brtl (1996): Theorem 9.1 (Brtl (1996)) Given metric
9 Grph Cutting Procedures Lst clss we begn looking t how to embed rbitrry metrics into distributions of trees, nd proved the following theorem due to Brtl (1996): Theorem 9.1 (Brtl (1996)) Given metric
AML710 CAD LECTURE 16 SURFACES. 1. Analytical Surfaces 2. Synthetic Surfaces
 AML7 CAD LECTURE 6 SURFACES. Anlticl Surfces. Snthetic Surfces Surfce Representtion From CAD/CAM point of view surfces re s importnt s curves nd solids. We need to hve n ide of curves for surfce cretion.
AML7 CAD LECTURE 6 SURFACES. Anlticl Surfces. Snthetic Surfces Surfce Representtion From CAD/CAM point of view surfces re s importnt s curves nd solids. We need to hve n ide of curves for surfce cretion.
1.1 Lines AP Calculus
 . Lines AP Clculus. LINES Notecrds from Section.: Rules for Rounding Round or Truncte ll finl nswers to 3 deciml plces. Do NOT round before ou rech our finl nswer. Much of Clculus focuses on the concept
. Lines AP Clculus. LINES Notecrds from Section.: Rules for Rounding Round or Truncte ll finl nswers to 3 deciml plces. Do NOT round before ou rech our finl nswer. Much of Clculus focuses on the concept
Naming 3D objects. 1 Name the 3D objects labelled in these models. Use the word bank to help you.
 Nming 3D ojects 1 Nme the 3D ojects lelled in these models. Use the word nk to help you. Word nk cue prism sphere cone cylinder pyrmid D A C F A B C D cone cylinder cue cylinder E B E prism F cue G G pyrmid
Nming 3D ojects 1 Nme the 3D ojects lelled in these models. Use the word nk to help you. Word nk cue prism sphere cone cylinder pyrmid D A C F A B C D cone cylinder cue cylinder E B E prism F cue G G pyrmid
Before We Begin. Introduction to Spatial Domain Filtering. Introduction to Digital Image Processing. Overview (1): Administrative Details (1):
 Overview (): Before We Begin Administrtive detils Review some questions to consider Winter 2006 Imge Enhncement in the Sptil Domin: Bsics of Sptil Filtering, Smoothing Sptil Filters, Order Sttistics Filters
Overview (): Before We Begin Administrtive detils Review some questions to consider Winter 2006 Imge Enhncement in the Sptil Domin: Bsics of Sptil Filtering, Smoothing Sptil Filters, Order Sttistics Filters
Lecture Overview. Knowledge-based systems in Bioinformatics, 1MB602. Procedural abstraction. The sum procedure. Integration as a procedure
 Lecture Overview Knowledge-bsed systems in Bioinformtics, MB6 Scheme lecture Procedurl bstrction Higher order procedures Procedures s rguments Procedures s returned vlues Locl vribles Dt bstrction Compound
Lecture Overview Knowledge-bsed systems in Bioinformtics, MB6 Scheme lecture Procedurl bstrction Higher order procedures Procedures s rguments Procedures s returned vlues Locl vribles Dt bstrction Compound
COMP 423 lecture 11 Jan. 28, 2008
 COMP 423 lecture 11 Jn. 28, 2008 Up to now, we hve looked t how some symols in n lphet occur more frequently thn others nd how we cn sve its y using code such tht the codewords for more frequently occuring
COMP 423 lecture 11 Jn. 28, 2008 Up to now, we hve looked t how some symols in n lphet occur more frequently thn others nd how we cn sve its y using code such tht the codewords for more frequently occuring
a(e, x) = x. Diagrammatically, this is encoded as the following commutative diagrams / X
 4. Mon, Sept. 30 Lst time, we defined the quotient topology coming from continuous surjection q : X! Y. Recll tht q is quotient mp (nd Y hs the quotient topology) if V Y is open precisely when q (V ) X
4. Mon, Sept. 30 Lst time, we defined the quotient topology coming from continuous surjection q : X! Y. Recll tht q is quotient mp (nd Y hs the quotient topology) if V Y is open precisely when q (V ) X
Algebra II Notes Unit Ten: Conic Sections
 Sllus Ojective: 0. The student will sketch the grph of conic section with centers either t or not t the origin. (PARABOLAS) Review: The Midpoint Formul The midpoint M of the line segment connecting the
Sllus Ojective: 0. The student will sketch the grph of conic section with centers either t or not t the origin. (PARABOLAS) Review: The Midpoint Formul The midpoint M of the line segment connecting the
CS201 Discussion 10 DRAWTREE + TRIES
 CS201 Discussion 10 DRAWTREE + TRIES DrwTree First instinct: recursion As very generic structure, we could tckle this problem s follows: drw(): Find the root drw(root) drw(root): Write the line for the
CS201 Discussion 10 DRAWTREE + TRIES DrwTree First instinct: recursion As very generic structure, we could tckle this problem s follows: drw(): Find the root drw(root) drw(root): Write the line for the
Fig.25: the Role of LEX
 The Lnguge for Specifying Lexicl Anlyzer We shll now study how to uild lexicl nlyzer from specifiction of tokens in the form of list of regulr expressions The discussion centers round the design of n existing
The Lnguge for Specifying Lexicl Anlyzer We shll now study how to uild lexicl nlyzer from specifiction of tokens in the form of list of regulr expressions The discussion centers round the design of n existing
Math 17 - Review. Review for Chapter 12
 Mth 17 - eview Ying Wu eview for hpter 12 1. Given prmetric plnr curve x = f(t), y = g(t), where t b, how to eliminte the prmeter? (Use substitutions, or use trigonometry identities, etc). How to prmeterize
Mth 17 - eview Ying Wu eview for hpter 12 1. Given prmetric plnr curve x = f(t), y = g(t), where t b, how to eliminte the prmeter? (Use substitutions, or use trigonometry identities, etc). How to prmeterize
ZZ - Advanced Math Review 2017
 ZZ - Advnced Mth Review Mtrix Multipliction Given! nd! find the sum of the elements of the product BA First, rewrite the mtrices in the correct order to multiply The product is BA hs order x since B is
ZZ - Advnced Mth Review Mtrix Multipliction Given! nd! find the sum of the elements of the product BA First, rewrite the mtrices in the correct order to multiply The product is BA hs order x since B is
Math 4 Review for Quarter 2 Cumulative Test
 Mth 4 Review for Qurter 2 Cumultive Test Nme: I. Right Tringle Trigonometry (3.1-3.3) Key Fcts Pythgoren Theorem - In right tringle, 2 + b 2 = c 2 where c is the hypotenuse s shown below. c b Trigonometric
Mth 4 Review for Qurter 2 Cumultive Test Nme: I. Right Tringle Trigonometry (3.1-3.3) Key Fcts Pythgoren Theorem - In right tringle, 2 + b 2 = c 2 where c is the hypotenuse s shown below. c b Trigonometric
WebAssign Lesson 1-3a Substitution Part 1 (Homework)
 WeAssign Lesson -3 Sustitution Prt (Homework) Current Score : / 3 Due : Fridy, June 7 04 :00 AM MDT Jimos Skriletz Mth 75, section 3, Summer 04 Instructor: Jimos Skriletz. /.5 points Suppose you hve the
WeAssign Lesson -3 Sustitution Prt (Homework) Current Score : / 3 Due : Fridy, June 7 04 :00 AM MDT Jimos Skriletz Mth 75, section 3, Summer 04 Instructor: Jimos Skriletz. /.5 points Suppose you hve the
Fall 2018 Midterm 1 October 11, ˆ You may not ask questions about the exam except for language clarifications.
 15-112 Fll 2018 Midterm 1 October 11, 2018 Nme: Andrew ID: Recittion Section: ˆ You my not use ny books, notes, extr pper, or electronic devices during this exm. There should be nothing on your desk or
15-112 Fll 2018 Midterm 1 October 11, 2018 Nme: Andrew ID: Recittion Section: ˆ You my not use ny books, notes, extr pper, or electronic devices during this exm. There should be nothing on your desk or
