Application of polynomial chaos in proton therapy
|
|
|
- Marilynn Phelps
- 5 years ago
- Views:
Transcription
1 Application of polynomial chaos in proton therapy Dose distributions, treatment parameters, robustness recipes & treatment planning Master Thesis S.R. van der Voort June, 215 Supervisors: Dr. Ir. D. Lathouwers Dr. Z. Perkó Delft University of Technology Faculty of Applied Sciences Department of Radiation Science and Technology Section of Nuclear Energy and Radiation Applications Dr. M. Hoogeman Dr. Ir. S. van de Water Erasmus MC Cancer Institute Department of Radiation Oncology Unit of Medical Physics
2
3 Abstract Proton therapy is a kind of radiotherapy which promises better treatments than radiotherapy using photons, which is currently the most widespread. However proton therapy is very sensitive to different kinds of uncertainties, among which patient setup errors and errors in the proton range. These errors can have a large effect on the dose distribution in the patient and therefore it is important to quantify their effect. Quantifying the effect of errors on the dose distributions is time consuming, and in this thesis polynomial chaos has been used to solve this problem. Polynomial chaos approximates an exact calculation by replacing the calculation with a set of polynomials, called the polynomial chaos expansion. This expansion can then be evaluated to very quickly determine the effect for a certain error. In this thesis polynomial chaos has been used to determine dose distributions in proton therapy under the effect of certain errors. The expansions are able to incorporate systematic and random errors and to very quickly determine the mean dose over a treatment, which would be almost impossible to do within a reasonable time using the dose engine. This was used to simulate different treatment parameters, e.g. a dose population histogram and a dose volume histogram. Two different groups of patients were considered, head and neck cancer patients and prostate patients. Polynomial chaos expansions were made for a total of 6 head and neck patients and 5 prostate patients to validate the accuracy of the expansions. The expansions took on average 8 and 55 minutes to be constructed for the head and neck, and prostate patients respectively. Validation of the accuracy was done using a gamma evaluation with a dose criterion of.1 Gy and a distance criterion of 1 mm for a total of 681 scenarios which covered 99% of the probability space. For the head and neck patients at least 9% of the voxels were accepted in 95% of the scenarios for the worst patient, the D 2 of the dose difference was less than 2 Gy for 9% of the scenarios. In the case of the prostate patients 9% of the voxels were accepted in 46% of the scenarios for the worst patient, with a D 2 less than 4 Gy for 9% of the scenarios. The result for the head and neck patients was acceptable and showed that for these patients the polynomial chaos expansion is a valid replacement of the dose engine. For the prostate patients these results were not acceptable, however using a higher accuracy in the construction of the expansion solved this problem but took significantly longer to construct. Once the polynomial chaos expansion was constructed the time needed to determine a dose distribution was on average 1 times faster for the head and neck patients and 7 times faster for the prostate patients than using the dose engine. A different type of polynomial chaos expansion was also made for different treatment parameters, to be able to quickly calculate them instead of using the expansion of the dose distribution as a basis. In this way it was possible to easily construct the bandwidth of a parameter. For some parameters the construction of the expansion required a lot of function evaluations, thus reducing the benefit of the expansion. Therefore multi-element polynomial chaos was applied, which reduced the number of evaluations needed and showed a good accuracy. The polynomial chaos expansions were also used to construct a robustness recipe for head and neck patients by looking at different combinations of systematic (Σ) and random (σ) errors. This robustness recipe prescribed the magnitude of the errors to be included in robust minimax optimization to get an adequate dose coverage in the high dose and low dose clinical target volume. A dose coverage of at least 95% of the prescribed dose for 98% of the volume (D 98 = 95%) was considered adequate. For unilateral patients the required setup robustness, SR, was SR =.15Σ σ Σ.6σ and SR =.7Σ σ Σ.7σ for bilateral patients. Lastly polynomial chaos expansions were used in probabilistic treatment planning as a proof of concept. Here a polynomial chaos expansion of the dose matrix was made, and 5 different scenarios were simulated to use in the optimization. The optimization was done using a conditional value at risk function, which took into account the high dose clinical target volume and the right parotid. Although this was just a proof of concept the results seemed promising.
4
5 List of symbols A D D α D F β He n lev N y n lev O p ξ R r k r V α x Dose matrix Dose Dose received by α % of volume Dose criterion used in gamma evaluation Optimization function for β-conditional value at risk Hermite polynomial of order n Quadrature level Number of y Number of quadrature points in quadrature level lev Polynomial order Probability density function of ξ Response of a system Expansion coefficient Distance criterion used in gamma evaluation Volume that receives a minimum of α% of the prescribed dose Beam weights α β β-value at risk λ Treatment parameter µ Mean Ψ Basis vector φ Single-dimensional polynomial φ β β - Conditional value at risk Σ Systematic error σ Standard deviation or random error ξ Random variable
6
7 List of abbreviations apc CDF CT CTV CVaR DPH DVH gpc GO HN IMPT LTCP MC ME-PC PC PCE PDF PO PTV OAR SR VaR Arbitrary polynomial chaos Cumulative distribution function Computed tomography Clinical target volume Conditional value at risk Dose population histogram Dose volume histogram Generalized polynomial chaos Grid order Head and neck Intensity modulated proton therapy Logarithmic tumour control probability Monte Carlo Multi-element polynomial chaos Polynomial chaos Polynomial chaos expansion Probability density function Polynomial order Planning target volume Organs at risk Setup robustness Value at risk
8
9 Acknowledgements I would like to thank my supervisors for their guidance and input in this project. Danny, thank you first of all for giving me the opportunity to do this project. You always managed to keep a broad overview of the project and helped by steering me in the right direction from time to time. Mischa, thank you for welcoming my at the Erasmus MC and all your input about the clinical side of things. The discussions with you were really helpful, and gave direction to the different clinical applications that I looked at. Steven, with your relaxed attitude it was a pleasure working with you. You were always willing to answer questions I might have, and helped me with all of the organisational things at the Erasmus MC. Hopefully our paths will cross again soon. Zoltán, thank you for helping me make my first steps into the world of polynomial chaos, your knowledge about the mathematical side of things helped me a lot. Our fruitful (no pun intended) discussions led to a lot of new ideas. I know we will work together again, and I am already looking forward to it. Joep, thank you for reading through my (sometimes very early and very rough) drafts and your comments. I would also like to thank you for the last 5 years, without you it would be ten times less fun and ten times as hard, Niet springen he. Georgina, thank you for (always) checking my English spelling, even when I spelled your name wrong afterwards (I spent extra attention to it this time, to make sure I got it correct). Wit beyond measure is man s greatest treasure
10
11 Contents 1 Introduction 1.1 Background Goals of this research Proton therapy 2.1 Overview of radiotherapy Patients Uncertainties in proton therapy Setup errors Range errors Treatment parameters Dose volume histogram V α D α Dose population histogram Treatment planning Gamma evaluations Polynomial chaos 3.1 Probability theory Gaussian distribution Quantifying the effects of uncertainty Polynomial chaos Basis vectors and basis set Determining expansions coefficients Quadratures Cubatures Sparse grids Extended sparse grids Hyperbolic trimming Global and local PCE Dose distributions 4.1 Constructing a PCE of the dose distribution Cutting out voxels Overview of PCE construction Evaluating the PCE Validating the expansion Choosing a grid order Gamma evaluations Absolute dose difference Timing results Applications DPH
12 4.5.2 Fractionation Treatment parameters Underdosage Treatment parameters 5.1 Constructing a parameter PCE λ-pce of the DVH λ-pce of the V Multi-element polynomial chaos Article: Robustness recipes 6.1 Introduction Methods and materials Patient data and dose prescriptions Treatment planning Treatment simulations Study design Results Discussion Conclusion Probabilistic treatment planning 7.1 Optimization problem Conditional value at risk Loss function PCE of dose matrix Optimization algorithm Results of optimization Conclusion 8.1 Future research A Derivation of global and local PCE B Validation of PCE
13 Chapter 1 Introduction 1.1 Background An estimated 3.2 million new cases of cancer were diagnosed in Europe in 28 [1], a significant increase from 2.9 million in 24 [2]. In the United States cancer was the second most common cause of death in 2 [3]. The extent and severity of the disease explain why research is being done to improve the treatment of cancer. Generally treatment of cancer can be divided into three treatment modalities; surgery, radiotherapy and chemotherapy. Each of the methods has its own advantages and disadvantages. For example surgery does not require the use of any radiation, which is beneficial for the patient. Radiotherapy on the other hand is a non-intrusive method as it does not require any operations to be performed on the patients. The treatment modality used for a certain patient depends on different factors like the tumour location and type. In this research the focus will be on radiotherapy, specifically proton therapy. Radiotherapy attempts to cure a patient using ionizing radiation to kill the cancer cells. However the radiation will also damage the healthy tissue, resulting in unwanted side effects. A higher amount of radiation will result in a higher amount of cancer cells being killed, but it will also mean a higher probability of complications in the healthy tissue. The energy deposited in a patient is called the dose. Proton therapy is a new kind of radiotherapy which promises treatments with fewer side effects than the currently applied photon therapy. However proton therapy is very sensitive to uncertainties that are present during a treatment. In Figure 1.1 two dose distributions are depicted, which show the treatment of the patient using proton therapy as it was expected and an example of a dose distribution that might result due to uncertainties. Here the dose throughout the patient is displayed, where the dose is indicated in Gray, the standard unit of dose. It can be seen that the actual dose distribution can differ greatly from the the expected situation. Therefore it is important to get a grasp on what the effect of different uncertainties on the dose distribution might be. The problem here is that the calculation of the effect of an uncertainty is rather time-consuming. A complete recalculation of the dose distribution is needed for every uncertainty, for example a recalculation is required for every x-position. Even for a single error it can already take up to a minute to determine the resulting dose distribution. Therefore a quicker method to calculate the resulting dose distributions and to quantify the effects of uncertainties is needed. The concept of proton therapy and different uncertainties that play a role is discussed in Chapter 2. In this research polynomial chaos will be used to more quickly obtain information about the effect of the uncertainties. Polynomial chaos constructs a meta-model of the problem by replacing the exact model with a set of polynomials, called the polynomial chaos expansion. 1
14 2 Chapter 1. Introduction (a) Dose distribution as expected. (b) Dose distribution as a result of errors. Figure 1.1: Comparison between dose distributions for the expected case and in the case of errors that might occur. These polynomials can be evaluated faster than the exact model, thus solving the problem of the slowness of the exact model. The polynomial chaos expansion has more advantages, for example it is easy to obtain the mean and variance of a problem directly from the polynomial chaos expansion, without doing any sampling of the expansion. Polynomial chaos is discussed in depth in Chapter Goals of this research Using polynomial chaos in proton therapy has already been researched [4]. Here a direct and indirect route were considered, where in the direct route a polynomial chaos expansion was made of a treatment parameter one was interested in. In the indirect route a polynomial chaos expansion was made of the dose distribution itself, and in this way it is possible to use the expansion to determine a dose distribution instead of only a parameter. In that research it was found that constructing an expansion the indirect way was hard, as it required too much memory, which restricted the accuracy that could be achieved. Therefore the first thing that will be done in this research is to find a way in which the memory requirement of the polynomial chaos expansion of the dose distribution can be reduced. This will then give the possibility of using the expansions to calculate dose distributions and not only parameters. Constructing a polynomial chaos expansion via the indirect route means that the direct route is not needed anymore. The expansion obtained using the direct route can be used to calculate different dose distributions, just as could be done using the dose engine. Using these dose distributions different parameters can be calculated, instead of using a polynomial chaos expansion via the direct route. It is important to verify the accuracy of these expansions to determine whether they can serve as a replacement of the exact calculation. Another interesting aspect is the effect of systematic and random errors. When a patient undergoes a radiotherapy treatment this is usually done in fractions, where a limited amount of dose is given in each fraction. Systematic errors are errors that remain the same over all of the fractions, but which differ from patient to patient. Random errors are errors that differ between fractions. Both of these errors have a different impact on the resulting dose distribution. Normally they could be simulated by sampling different random errors for a single systematic error and determining the resulting dose distribution. However this can be very time consuming and therefore it might be interesting to see whether it is possible to use the polynomial chaos expansions to very quickly get the mean dose over the fractions. Making a polynomial chaos expansion, verifying its accuracy and the effect of systematic and random errors are the subject of Chapter 4. If one is only interested in a certain parameter which describes the dose distribution, for
15 1.2. Goals of this research 3 example a dose volume histogram, it might be better to construct a polynomial chaos expansion of that parameter instead of the whole dose distribution because it is faster to evaluate the expansion of a parameter than that of the whole dose distribution. This was also the idea behind the direct route, however in the direct route no systematic errors were taken into account, which is needed to properly describe the parameters. Therefore in Chapter 5 the possibility of constructing a polynomial chaos expansion of a certain treatment parameter is considered. In proton therapy there is a lot of research being done on robust treatment planning. Robust treatment planning means that a treatment plan is made, which even in the presence of errors will ensure a good dose distribution. At the moment this is mainly done using minimax optimization, which takes into account multiple pre-defined error scenarios. During the treatment planning these pre-defined scenarios are taken into account, and it is ensured that a good dose distribution occurs for those scenarios. The idea is that by taking into account these scenarios the dose distribution will also be acceptable for other possible scenarios. However it is currently unknown what the magnitude of the errors to be included in the optimization should be. Because polynomial chaos can be used to very quickly determine the effects of the errors it will be used to see if the scenarios can be chosen in such a way that a group of patients will get an adequate treatment. This will be the subject of Chapter 6. Another approach of treatment planning is probabilistic planning. Probabilistic planning is interesting as it uses only statistical information about the different errors to make a treatment plan. The pre-defined scenarios used in minimax optimization are usually the same for all patients. However these scenarios might not be optimal for all patients, resulting in a larger than necessary dose in the healthy tissue. Probabilistic treatment planning does not use pre-defined scenarios, but it more directly takes into account the uncertainties. Of course this requires a fast calculation to keep the time needed to construct a treatment plan reasonable. Fast sampling is the reason why polynomial chaos will be used and therefore it might be interesting to see if it can be used to make treatment plans. This will be the focus of Chapter 7.
16
17 Chapter 2 Proton therapy 2.1 Overview of radiotherapy The idea behind radiotherapy is to treat the patient with ionizing radiation. In this way the DNA of the tumour cells can be damaged, which will result in cancer cells being killed, hopefully leading to a successful treatment of the tumour [5]. The amount of energy deposited is called the dose, which is expressed in Gray (Gy), where a higher dose means a higher amount of radiation and as a result leads to a higher amount of cells being killed. Healthy tissue is also sensitive to ionizing radiation, however when the same amount of dose is given to healthy tissue and cancer cells, usually a larger fraction of the healthy tissue cells will survive than cancer cells. Moreover, healthy tissue can repair the damage that has been inflicted faster than the cancer cells can repair themselves. To benefit from this the dose is usually not given all at the same time, but is split up into several fractions. In each fraction only part of the total dose is given to give the healthy tissue a chance to repair itself between fractions. The number of fractions given depends on the prescribed dose and tumour location, but usually a treatment consists of around 3 to 4 daily fractions. As mentioned earlier, the ionizing radiation will also damage the healthy tissue, which can have negative consequences. For example a new tumour can develop as a result of the radiation [6, 7] or organs might get damaged resulting in problems with their functionality [8 1]. Healthy tissue that might experience negative consequences as a result of the radiation treatment are called organs at risk (OARs). The challenge of radiotherapy lies in trying to get a high enough dose to the tumour to kill the cancer cells while keeping the dose in the OARs low enough to limit the possibility of negative consequences. In this regard proton therapy can play an important role. Currently the most often applied type of radiotherapy is photon therapy. However the profile of a photon beam is not ideal for sparing OARs, as can be seen in Figure 2.1. Here the dose as a function of the depth is displayed for a mono-energetic photon and a proton beam. The maximum dose of the photon beam is deposited at the entrance, after a small region where there is a build-up of the dose, and then drops off exponentially. As a result the dose is high over a long range, which means that there is also a high dose before and behind the tumour, where OARs might be located. The different shapes of the photon and proton beam originates from the physical properties of photons and protons. Photons are indirectly ionizing particles whereas protons are massive (compared to the electrons), directly ionizing particles. As a result the protons will not transfer a lot of energy at the beginning of their range, when they have a high velocity, which means that the deposited dose is low. The protons will gradually slow done and at the end of their range when their velocity is low they will deposit a high dose. As a result the maximum dose will be concentrated at a 5
18 6 Chapter 2. Proton therapy single depth (for protons of the same energy), called the Bragg peak. In front of the Bragg peak the deposited dose is low, whereas behind the Bragg peak there is no dose deposited anymore because all of the protons are stopped. Therefore when the Bragg peak is positioned inside the tumour the dose to the tumour will be high, while the dose to the surrounding tissue will be low. 1 9 Photon Proton 8 7 Dose (%) Depth (cm) Figure 2.1: Dose as a function of the depth for a photon and proton beam. The shape of the proton beam is advantageous for the sparing of healthy tissue. However the shape of a proton beam is also a disadvantage. When for some reason the Bragg peak ends up at a different location than intended, the difference in the dose can be large, as shown in Figure 2.2. It can be seen that the position of the Bragg peak is displaced a little, resulting in a higher dose at a more shallow depth and almost no dose at the position where the Bragg peak was originally located. This problem is limited in photon therapy, because of the profile of the photon beam the dose difference when the beam is shifted is small Tumour Photon Proton Photon, displaced Proton, displaced 7 Dose (%) Depth (cm) Figure 2.2: Difference in the delivered dose when a shift occurs. For the proton beam the difference in dose is much larger. As a result the given dose in a proton therapy treatment can differ significantly from the dose that was expected to be given [11]. Therefore it is important to quantify what happens to the dose distribution as a result of different uncertainties that might occur. When treating a patient, multiple proton beams as the one shown in Figure 2.1 (referred to as proton pencil beams or beamlets) are needed in to deliver the dose. In this work intensity modulated proton therapy (IMPT) has been used, where each pencil beam is assigned a different intensity Patients Before considering different types of uncertainties, first the patients that will be considered in this work are introduced. The two types of patients that will be looked at are head and neck cancer patients and prostate patients. These patients were chosen as it was shown that they benefit
19 z(mm) z (mm) 2.2. Uncertainties in proton therapy 7 from proton therapy [12 15]. Head and neck (HN) patients can be subdivided into unilateral and bilateral patients, which means that the tumour is either on one side or on both sides of the neck. An example of a unilateral head and neck patient can be seen in Figure 2.3, a bilateral head and neck patient is shown in Figure 2.4 and a prostate patient is displayed in Figure 2.5. The orientation and coordinate system of the patient can be seen in Figure 2.6. These figures show computed tomography (CT) scans, which are made when a patient first comes into the clinic. In these CT scans a physician delineates the clinical target volume (CTV), which is the visible tumour and a margin to account for spread of the cancer that is not visible [16]. The CTV is divided in a part with a higher dose prescription, the CTV high and a lower dose prescription, the CTV low. Furthermore the OARs are also delineated. The delineated volumes are referred to as structures. The function of some of the OARs is given in Table 2.1 for the head and neck patients. For computational purposes the CT image of the patient is divided in small elements called voxels, where on average a CT image consists of approximately 1 to 5 million voxels. When a dose distribution is calculated this means that the dose in every voxel is determined, this is done using a so-called dose engine. A total of six head and neck patients (three unilateral and three bilateral), and five prostate patients will be used throughout different parts of this thesis CTV high CTV low Oral cavity SMG (right) z (mm) CTV high CTV low Larynx Parotid (left) Parotid (right) Swal. Mus. y (mm) CTV high CTV low Cord Parotid (left) Parotid (right) Oral cavity SMG (left) SMG (right) Swal. Mus y (mm) 15 (a) Side view of patient x (mm) (b) Front view of patient x (mm) (c) Top view of patient. Figure 2.3: CT image of a unilateral head and neck cancer patient. 75 CTV high CTV low Brainstem Cord Larynx Oral cavity Swal. Mus. z (mm) CTV high CTV low Larynx Parotid (right) Parotid (left) Swal. Mus. y (mm) CTV high CTV low Cord Oral cavity Parotid (left) Parotid (right) SMG (left) SMG (right) Swal. Mus y (mm) 15 (a) Side view of patient x (mm) (b) Front view of patient x (mm) (c) Top view of patient. Figure 2.4: CT image of a bilateral head and neck cancer patient. 2.2 Uncertainties in proton therapy Proton therapy is very sensitive to the effect of different uncertainties that might occur during the dose delivery. Due to the different uncertainties the protons can end up at a different location than expected, which will mean that the given dose distribution is not the same as the planned dose distribution.
20 y (mm) 8 Chapter 2. Proton therapy z (mm) y (mm) Prostate Bladder Bowel cavity Rectum Seminal vesicles 5 (a) Side view of patient. z (mm) Prostate Bladder Bowel cavity x (mm) Femur head (left) Femur head (right) Lymph nodes (b) Front view of patient. x (mm) (c) Top view of patient. Figure 2.5: CT image of prostate patient. z y x Figure 2.6: Coordinate system defined for the patient. Structure CTV Parotid SMG Cord Brain stem Larynx Oral cavity Swal. Mus. Description Tumour plus a margin for invisible spread of cancer The parotid gland produces saliva Sub mandibular gland, produces saliva Spinal cord, contains the nerves Connects spinal cord and brain Involved in breathing and sound production First part of the mouth Collection of different muscles associated with swallowing Table 2.1: Overview of different structures that have been delineated in the CT images for a head and neck patient.
21 2.2. Uncertainties in proton therapy 9 Generally the type of uncertainties can be divided into two categories, intra-fraction uncertainties are uncertainties which can change during the delivery of a treatment fraction and inter-fraction uncertainties, which stay the same over a fraction but can differ from fraction to fraction [17]. An example of an intra-fraction uncertainty is the respiratory motion in the case of a lung tumour. No intra-fraction uncertainties will be considered in this work Setup errors An inter-fraction uncertainty that is taken into account is the setup error. When irradiating the patient it is important that the patient is in the same position as when the CT image was made. Because the CT image is used to make a treatment plan (which will be explained in section 2.4) a misalignment of the patient will mean that the proton beams will enter the body of the patient at a different position, thus resulting in a different dose distribution. Different methods exist which try to minimize this error, for example by placing markers inside the patient. Before each treatment fraction a radiograph is made of the patient and the markers are then aligned to their reference position [18]. Another method is to apply tattoos to the patient and align lasers with these tattoos before the treatment [19]. One could also use the bony anatomy of the patient to align the patient. Although these methods will reduce the setup errors, they are not entirely eliminated. Setup errors can occur along the x-, y- and z-axis of the patient as seen in Figure 2.6. A specific instance of an error is referred to as a shift. Setup errors can be divided into two types, systematic and random errors. A systematic error is an error that is different for different patients, but stays the same over each fraction that the patient receives. Random errors on the other hand also differ from fraction to fraction. A schematic of the difference between systematic and random setup errors can be seen in Figure 2.7. Random setup errors are caused by the small misalignment of the patient before each treatment fraction is given. Systematic setup errors might occur for example when the markers which were implanted have moved or when the internal anatomy of the patient has changed compared to the CT image. It is clear that the systematic and random error have a different effect on the dose distribution and therefore their effect should be simulated in a different way. The position that a patient is in at a certain fraction is the sum of the systematic and random error, referred to as the total or combined error. Systematic and random errors are also often referred to in the context of a population and individual patients. In this case each individual patient does not necessarily have to be a different patient, but is often considered as the same patient with a different systematic shift occurring. When a lot of different systematic shifts are taken into account this forms the population. σ σ σ Σ Σ σ σ σ Figure 2.7: Schematic of systematic, Σ, and random, σ, setup errors. The green and red patient have a different systematic error and receive 3 fractions, each with a different random error Range errors The other uncertainty that will be taken into account is the uncertainty in the range of the protons, which is expressed as a relative and absolute range error. The relative range error comes from the fact that the proton range is based on the CT image of the patient, where CT values are converted to the proton stopping power from which the proton range is determined. However there is no direct relationship between the CT values and the proton stopping power,
22 1 Chapter 2. Proton therapy because the CT image is made using photons which interact differently with matter than the protons. Therefore the conversion is based on previously done measurements or Monte Carlo simulations, which will introduce an error in the calculated proton range [2, 21]. Because the relative range error originates from the CT image of the patient it is inherently a systematic error. The absolute range error is given as a direct error in the range, not based on the CT image. Only the relative range error will be taken into account when calculating dose distributions, however the absolute range error is sometimes used during treatment planning. From now on, unless explicitly mentioned, the range error will always mean the relative range error. Taking all of the above errors into account means that the dose distribution will depend on a total of four variables; three setup errors, one for each direction, and the range error. The dose distribution for setup and range shifts can be calculated using the dose engine used by the Erasmus MC [22]. The dose engine calculates the dose distribution for a treatment plan for a given combination of the setup and range error, called a scenario. This dose engine was slightly adapted by changing the way the relative range error is calculated. Previously this was done by changing the energy of the proton beam, as this would also influence the range of the protons. Although scaling the energy of the proton beam is faster, the range error is actually defined as a percentage of the values of the CT images and therefore it will be simulated in this way. The difference between scaling the energy and the CT image can be seen in Figure 2.8. For a single voxel the dose as a function of the range shift is depicted here, by scaling the energy and by scaling the CT image. In the case where the energy is scaled a stepwise pattern is visible, which comes from the fact that the energy can not be scaled arbitrarily because the range of the proton beam is given for a limited number of proton energies. When the scaled energy is not in this list the energy closest to it is used, which means that small differences in the energy will ultimately give the same proton range. 65 Scaling energy Scaling CT 6 Dose (Gy) Range shift (%) Figure 2.8: Effect of range shift in a voxel determined by scaling the energy and the CT image. The systematic and random setup error and range error are all assumed to be Gaussian distributed. When talking about these errors they are defined by their standard deviation, e.g. a 2 mm setup error means that the standard deviation of the error is 2 mm. The standard deviation of the systematic errors and random errors is denoted as Σ and σ respectively. Unless otherwise mentioned the systematic and random setup error are assumed to have a 2 mm standard deviation for all three directions, and the range error to have a 2% standard deviation. This is based on the fact that a 3 mm and 3% error cover 85% of the probability space, which corresponds to 1.5σ based on the Gaussian distribution [23]. When applicable absolute range errors are expressed in mm.
23 2.3. Treatment parameters Treatment parameters To describe the dose distribution, various parameters are used in radiotherapy. Of course one could always look at the dose distribution itself, but the treatment parameters can give physicians a quick overview of the dose that is delivered. Furthermore they can be a handy tool to visualize the dose distribution as it is hard to depict the full dose distribution in a single figure. In this section different treatment parameters will be presented. The different treatment parameters are defined over a whole treatment of a patient, that is they are defined as a function of the mean dose over the fractions Dose volume histogram One of the most commonly used parameters is the dose volume histogram (DVH), an example of which is depicted in Figure 2.9. A DVH is a cumulative histogram which shows the fraction of the volume that receives at least a certain dose. A DVH can be constructed for different structures. For example in Figure 2.9 it can be seen that for the CTV high 1% of the volume receives a dose of at least 6 Gy of the dose and no dose above 7 Gy is present. In this way it is possible to determine whether the dose in the different structures is acceptable, e.g. whether the dose in the CTV is high enough while the dose in OARs is below a maximum allowed dose CTV high CTV low Cord Parotid Volume (%) Dose (Gy) Figure 2.9: Example of a dose volume histogram. For a unilateral head and neck patient the DVH of different structures is shown V α Instead of representing the DVH as a figure one could also look at a fraction α of the prescribed dose and then determine V α = 1 N voxels N voxels i=1 δ(d i αd pres ) (2.1) where N voxels is the number of voxels in the structure, D i is the dose in voxel i, D pres is the prescribed dose expressed and δ(d i D α ) is 1 when D i D α and otherwise. In this way the fraction of the volume of a structure that receives at least a specified dose is determined. Often used are the V 95 and V 17 for the CTV which give the volume that receives 95% and 17% of the prescribed dose respectively. This can be used as a requirement on the dose in the CTV, e.g. V 95 = 1% means that the whole CTV should receive a dose of at least 95% of the prescribed dose.
24 12 Chapter 2. Proton therapy D α In contrast to the V α, which looks at the volume that receives a certain dose, one could also use the D α, which is the maximum dose received by at least α% of the volume. D α is defined as D α = P 1 α (D) (2.2) where P 1 α (D) is the (1 α)th percentile of the dose for a certain structure. For example the D 2 is the maximum dose such that at least 2% of the volume receives this dose, and D 5 is the median of the dose. The higher α, the lower the D α will be. From the definition of the V α and D α it is obvious that if V α = β then D β = V α and vice versa. Often used are the D 2 to indicate the maximum dose in a structure and the D 98 as a minimum dose. This is done because the real maximum and minimum dose are the dose from a single voxel, which means that if a single voxel receives a very high or a very low dose the minimum and maximum dose would be an extreme value. As the dose in a single voxel is not really important the D 2 and D 98 are used, as they solve this problem by taking into account a small volume instead of a single voxel Dose population histogram The previously mentioned parameters are a function of the mean dose over a treatment, but they do not show the effect of the systematic errors, which is where a dose population histogram (DPH) is useful [24]. A DPH is constructed by simulating different systematic errors and for each systematic error determining the mean dose over the fractions, or a parameter based on it. A cumulative histogram is made of the dose parameter determined for each systematic error, which will give information about the distribution of that parameter in the population. An example of a DPH is displayed in Figure 2.1. Here the D 98 is used as a dose parameter and it can be seen that 7% of the population receives a D 98 of 98%. This kind of analysis can be used to evaluate the quality of a plan when taking into account systematic errors as it can give a good idea about the resulting dose in a population Population (%) D 98 (%) Figure 2.1: Example of a dose population histogram. The D 98 of the CTV high was determined for different systematic errors to simulate a population. 2.4 Treatment planning Once a CT image has been made of the patient, the next step is to make a treatment plan. In the case of IMPT a treatment plan prescribes which pencil beams should be used and with which intensity, depending on the prescribed dose to the CTV and OARs. The goal of treatment planning is to make sure that a sufficient dose is given to the CTV while minimizing the dose to the OARs as much as possible.
25 2.4. Treatment planning 13 Treatment plans can be made manually by a treatment planner or using automatic treatment planing, of course a combination of the two is also possible. In this thesis automatic treatment planning is done using icycle [25]. icycle is an automatic treatment planning system which makes use of wish-lists to take into account the CTV and different OARs, the wish-list used for head and neck patients in this thesis is given in Table 2.2. To be able to make treatments plans for IMPT, proton beam resampling [26] is used. Proton beam resampling first randomly selects a number of pencil beams from a very fine grid to be included in an optimization iteration, after which the optimization is performed. After the optimization iteration the beams that have a low contribution are thrown out and new pencil beams are randomly selected to add to the current set. This is repeated for each optimization iteration. Constraints Structure Type Limit CTV high Minimum Gy CTV intermediate Minimum Gy CTV low Minimum Gy Objectives Priority Structure Type Goal 1 CTV high Maximum Gy 1 CTV intermediate Maximum Gy 1 CTV low Maximum Gy 3 Parotid Mean Gy 4 Submandibular glands Mean Gy 5 Cord Maximum 2 Gy 5 Brain stem Maximum 2 Gy 6 Larynx Mean Gy 6 Oral cavity Mean Gy 7 Swallowing muscles Mean Gy Table 2.2: Wish-list describing the dose prescriptions used in this study. The order in which the objectives were optimized is indicated by the priority where a lower priority number means a higher priority. The CTV intermediate is a 1 mm transition region between the high-dose and low-dose CTV. The CTV-low consists of the low-dose CTV excluding the transition region. To account for the uncertainties that can occur during treatment, robust planning is used. With icycle minimax (worst-case) optimization is performed [27, 28]. In minimax optimization the dose is calculated for a limited number of scenarios, called planning scenarios. For all of these scenarios the dose is evaluated and the values of the optimization functions are determined. The worst case value for each optimization function separately is taken and optimized. Prior to the optimization one needs to select a setup and range robustness. These define the scenarios that are taken into account during optimization. The first scenario that is included in the optimization is always the nominal scenario, the scenario without any errors occurring. The setup robustness defines a shift in both the positive and negative direction for all three of the directions, which gives six additional scenarios. For the range robustness both a relative and absolute range shift can be set separately. The absolute and relative range shifts are then both applied in the positive and negative direction simultaneously, giving two more scenarios. Thus in total nine planning scenarios are included in the optimization. It is important to note that there are no scenarios with cross-terms, i.e. no scenario with errors simultaneously in the x and y direction or a setup and range error. A plan will be defined by its robust settings, e.g. when talking about a (3,2,)-plan this means that a 3 mm setup robustness, 2% relative range robustness and mm absolute range robustness was used. The nine planning scenarios included for a (α, β, γ)-plan are given in Table 2.3. The scenarios included in a (3,3,1)-plan are
26 14 Chapter 2. Proton therapy the standard planning scenarios [29], and these scenarios will be used in different parts of this thesis. x-shift y-shift z-shift relative range shift absolute range shift mm mm mm % mm α mm mm mm % mm α mm mm mm % mm mm α mm mm % mm mm -α mm mm % mm mm mm α mm % mm mm mm -α mm % mm mm mm mm β % γ mm mm mm mm -β % -γ mm Table 2.3: Planning scenarios included in the robust optimization for a (α, β, γ)-plan. 2.5 Gamma evaluations Historically gamma evaluations are used to quantify the difference between a measured and calculated dose distribution [3, 31], but in general it can be used to compare any two dose distributions. In this way it can be checked whether the dose calculation is acceptable or whether it differs too much from the delivered dose. Of course this could be done by just comparing the dose in each voxel and then calculating the difference. However this can give an unfair representation in regions where there is a large dose gradient, e.g. at the edge of the CTV. When a large gradient is present the dose in the same voxel in both of the distributions can differ greatly when there is a small spatial error. A neighbouring voxel might give a better dose prediction and a small distance between the voxels is then acceptable. To account for this the gamma evaluation does not just directly compare the voxels of two distributions, but it also searches in a small neighbourhood around each voxel to possibly find a better agreement of the dose. In this way the gamma evaluation can give a simple overview of the difference between two dose distributions. In this work gamma evaluations will be used to compare dose distributions obtained from two different calculations, to check whether the difference between them is acceptable. The gamma value is defined as ) { )} γ (r e = min Γ (r e, r c {r c } (2.3) at a point r e in the exact dose ) distribution where r c is a point in the dose distribution with which it is compared. Γ (r e, r c is defined as ) Γ (r e, r c = ( ) 2 ) )) 2 r e r c (D e (r e D c (r c r 2 + D 2 (2.4) where D is the dose criterion and r is the distance criterion. From this equation it can be seen that gamma evaluation will compare voxels ) in a certain region and determine the best possible option. A voxel is accepted when γ (r e 1 and rejected otherwise. Thus comparing two dose distributions using a gamma evaluation will determine for each voxel whether it has passed or failed. The extreme cases of a voxel being accepted can be either two voxels at the
27 2.5. Gamma evaluations 15 same position but with a dose difference D or voxels a distance r apart but with no dose difference. Obviously the lower D and r are set the stricter the gamma evaluation is. Although Equation (2.3) is defined over all r c, in general only a small region around a voxel is searched, ( 2 because when r e r c ) r 2 the voxel has already failed the gamma evaluation, regardless of the dose difference, and searching a larger region will not resolve this.
28
29 Chapter 3 Polynomial chaos In the previous chapter proton therapy was introduced and the uncertainties that play a role in a proton treatment were discussed. In this chapter polynomial chaos will be discussed, with which the effects of the different uncertainties can be quantified. Large parts of this chapter are based on Le Maître [32], Perkó [33] and Xiu [34]. 3.1 Probability theory Probability theory plays a big role when uncertainty is involved, as it can give a measure of the uncertainty that is being dealt with. Therefore before going further an overview is given of probability theory to allow for a proper description of uncertainties. To describe probabilities a sample space Ω is defined, with θ Ω a random event within the sample space. The set of possible outcomes is denoted as F where the outcomes have a probability measure P. This constructs a probability space: (Ω, F, P). The focus of this research will be on real valued stochastic responses, R(θ), which maps the sample space to R, R(θ) : Ω R (3.1) All of the responses are assumed to belong to the L 2 space, where the L 2 space is defined as in Equation (3.2) where denotes and and, denotes the inner product in L 2, defined in Equation (3.4). L 2 (Ω, P) = {R(θ) : [R(θ) : Ω R] [ R, R < ]} (3.2) The random events θ can be described by a random vector ξ(θ) = (ξ 1 (θ), ξ 2 (θ),..., ξ Ndim (θ)) T (3.3) for a total of N dim variables. The random vector ξ describes the values of different variables for a realization of θ. From now on will be used to indicate a vector. The inner product in the L 2 -space is defined as Q, S = Θ Q(θ)S(θ)dP(θ) = D(Θ) ( ) ( ) Q ξ(θ) S ξ(θ) p ξ dξ (3.4) where D(Θ) is the domain of the random variables. From now on ξ j (θ) will be written as ξ j, because it is assumed that showing the explicit dependence on θ is not needed for understanding the rest of the theory. 17
30 18 Chapter 3. Polynomial chaos In this work the different random variables ξ j are assumed to be independent. Each random variable has a probability density function (PDF), p ξj (ξ j ), associated with it, which describes the probability of the random variable taking on a certain range of values (in the continuous case). Because the random variables are assumed to be independent it is easy to determine the joint probability density function, which is just the product of the individual PDFs, p ξ (ξ) = N dim j=1 p ξj (ξ j ) (3.5) The joint PDF describes the probability of each of the different variables lying within a certain range of values. Throughout this thesis the assumption has been made that the PDFs of the random variables are known. The most common quantities of interest when dealing with random variables are usually the mean, which is the average outcome of an experiment when it is repeated many times, and the variance, which is a measure of the spread in the results. The mean is defined as and the variance as µ R = E[R] = ( ) ( ) Var(R) = E[(R ξ E[R ξ ]) 2 ] = ( ) R ξ p ξ dξ (3.6) Usually the standard deviation is used instead of the variance, ( ) (R ξ µ R ) 2 p ξ dξ (3.7) σ R = Var(R) (3.8) Gaussian distribution Of particular interest are Gaussian distributions (also called normal distributions) as it is assumed that the setup and range errors are independent Gaussian distributed variables. A Gaussian distribution with mean µ and standard deviation σ is given by A variable with such a Gaussian distribution is notated as ) p ξ (ξ = 1 σ (ξ µ) 2 2π e 2σ 2 (3.9) X N (µ, σ 2 ) (3.1) Gaussian distributions have a few interesting properties. The first one being that it is easy to construct a Gaussian distribution with arbitrary mean and variance from a unit normal distribution X N (, 1), by scaling the distribution, Y = µ + Xσ (3.11) Another interesting property is that Gaussian distributions can easily be summed to form a new Gaussian distribution. Let X N (µ X, σx 2 ) and Y N (µ Y, σy 2 ) then a new Gaussian distribution can be formed by addition of the two, Z = X + Y Z N (µ X + µ Y, σ 2 X + σ 2 Y ) (3.12)
31 3.2. Quantifying the effects of uncertainty Quantifying the effects of uncertainty There are different ways to quantify the effects of uncertainty, although the most common one is Monte Carlo (MC) sampling. The idea behind Monte Carlo sampling is rather simple, repeat a simulation a large number of times and in this way obtain statistics about the problem. When the number of sampling points is large enough the mean and variance obtained from MC sampling are close to the actual mean and variance of the problem. Monte Carlo sampling works for every problem and it is simple to perform, however it has a big disadvantage as it can be rather slow to execute. Usually to get a statistically significant result from the MC sampling many sampling points are needed. When the simulation is slow, as is the case with the dose engine, it can take a long time to determine the output for all of the MC samples. Furthermore, a MC simulation gives only limited information. Usually the mean, variance and possibly higher statistical moments are obtained. Spectral methods can be a solution to the problems associated with MC simulations. Spectral methods expand the response of a problem in basis vectors, which can give more information than MC sampling. In this case Polynomial Chaos (PC) [35] will be used, which is a metamodel of the exact problem and contains most of the information that is contained in the exact model. Originally polynomial chaos was introduced by Wiener as Homogeneous chaos which could only take into account uncertainties which have Gaussian distributions. Polynomial chaos has since been expanded to also include other types of distributions, referred to as generalized polynomial chaos (gpc) [36] and in recent years it has been applied to a broad range of problems [4, 37 39]. The advantage of polynomial chaos lies in the fact that it requires a limited number of simulations to construct a polynomial chaos expansion (PCE), while it can give most of the information that is contained in the exact model. Once the polynomial chaos expansion has been obtained, it can be used to quickly calculate the effects of a certain realization of the variables. In the case of the dose engine this means that the dose distribution can be quickly calculated for a certain scenario using the PCE, much quicker than when the dose engine is used. Furthermore in the next section it will be shown that once the PCE has been constructed is easy to obtain the mean and variance of the problem. 3.3 Polynomial chaos The basic idea of polynomial chaos is to write the exact output, R, as a function of the uncertain inputs, ξ, ( ) R ξ = k= ) r k Ψ k (ξ (3.13) where r k are the expansion coefficients which need to be determined and Ψ k are different ( ) basis vectors, which are polynomials that depend on ξ. In the case of the dose engine R ξ represents the dose distribution for a certain scenario with shifts ξ. As 4 errors (3 setup errors and the range error) are taken into account, ξ is a four-dimensional vector. The coefficients are calculated as ( ( ) R ξ ), Ψ k ξ r k = ( ( ) (3.14) Ψ k ξ ), Ψ k ξ At this point the expansion in Equation (3.13) is an exact representation of the actual response, because an infinite number of polynomials are taken which will always be able to reconstruct the true response (assuming a continuous response). Because of practical limitations the PCE is truncated to contain only a limited number of basis vectors
32 2 Chapter 3. Polynomial chaos ( ) ( ) R ξ R P ξ = P k= ) r k Ψ k (ξ (3.15) where P + 1 is the total number of basis vectors kept in the expansion. To write the basis set of polynomials that are kept in the expansion, start off with the multi-index γ = (γ 1,..., γ Ndim ), where γ i indicates the polynomial order used in the i-th dimension. From this the multi-index set λ(o) for a certain polynomial order o can be constructed as Ndim λ(o) = γ : γ j = o (3.16) Then for a certain maximum polynomial order (PO), O, the basis set, the set of basis vectors included in the expansion, is given by Ndim L(O) = λ(o) = γ : γ j O (3.17) o [,1,...,O] The total number of basis vectors P +1 in the expansion depends on the number of dimensions N dim and the maximum polynomial order O j=1 P + 1 = (N dim + O)! N dim!o! j=1 (3.18) It is clear that in the case of independent random variables the dimensionality of a problem is fixed and thus the number of basis vectors is determined by the polynomial order. A higher polynomial order will mean a more accurate PCE (assuming that the expansion coefficients can be determined accurately) but will also mean that more expansion coefficients need to be determined Basis vectors and basis set ) The basis vectors, Ψ k (ξ, that are used in the expansion are constructed using a tensor product of the different single-dimensional polynomials φ, Ψ = N dim j=1 φ j,γj ( ξ j ) (3.19) The multi-index γ = (γ 1,..., γ Ndim ) indicates the polynomial order of the different dimensions, whereas the index j indicates the different random variables. The basis vectors are chosen as orthogonal polynomials, see Equation (3.2) where h 2 k is the norm of the basis vector and δ k,l is the delta function. ( ( ) Ψ k, Ψ l = Ψ k (ξ )Ψ l ξ )p ξ ξ dξ = h 2 kδ k,l (3.2) D(Θ) Choosing orthogonal φ will automatically result in orthogonal Ψ, as the different variables are assumed to be independent. The type of one-dimensional polynomial, φ, that can best be used for a certain variable depends on the probability distribution of that variable. For the most common distributions the type of polynomials are given in the Wiener-Askey scheme [36], which is partly given in Table 3.1. Although it is possible to use a different type of polynomial than the one in the Wiener-Askey scheme for a certain distribution, a higher polynomial order is then needed to achieve the same accuracy as in the case of the optimal polynomial type suggested by the scheme. The optimality of a type of polynomial for a certain distribution comes from the fact that the weighting function of certain types of polynomials is the same as, or very similar to, the PDF of the distributions that they are associated with.
33 3.3. Polynomial chaos 21 Distribution Polynomial Support Beta Jacobi [a, b] Gamma Laguerre [, ) Gaussian Hermite (, ) Uniform Legendre [a, b] Table 3.1: Wiener-Askey scheme of polynomials for some continuous distributions. Using this scheme the type of polynomial that can best be used for a certain PDF can be determined. Because the basis vectors are chosen orthogonal it is easy to determine the mean and variance of the response directly, without the need for any sampling. In Equation (3.21) it is shown that the mean is just the first coefficient of the PCE where the fact that Ψ = 1 and the orthogonality of the polynomials have been used. In Equation (3.22) the variance of the response is given, based only on the coefficients of the expansion and the norm of the polynomials. µ R = = = ( ( ) R ξ )p ξ ξ dξ = Ψ k= r k Ψ, Ψ k k= k= ( ) r k Ψ k (ξ )p ξ ξ dξ ( ) r k Ψ k (ξ )p ξ ξ dξ (3.21) = r ( ( ) ) 2 ( σr 2 = R ξ µ R pξ ( ) 2pξ ( ) = R ξ ξ dξ ) ξ dξ ( ( ) 2µ R R ξ )p ξ ξ dξ + ) µ 2 Rp ξ (ξ dξ = rk 2 Ψ k, Ψ k 2µ R Ψ, Ψ k + µ 2 R k= k= P = rkh 2 2 k µ 2 R = rkh 2 2 k rkh 2 2 k k= k=1 k=1 (3.22) Hermite polynomials In this research random variables which have a Gaussian distribution will be used and therefore as suggested by the Wiener-Askey scheme probabilists Hermite polynomials are used as the single-dimensional polynomials. The hermite polynomials are built using a recurrence relation, Equation (3.23). He 1 (ξ) = He (ξ) = 1 He n+1 (ξ) = ξhe n (ξ) He n(ξ) (3.23) They can also be determined directly, He n (ξ) = ( 1) n e ξ2 2 d n 2 dξ n e ξ 2 (3.24)
34 22 Chapter 3. Polynomial chaos where the relation to the Gaussian distribution, Equation (3.9), can clearly be seen. If a problem has three dimensions, each with a Gaussian distribution a possible basis vector would be He 1 (ξ 1 )He 3 (ξ 2 )He 2 (ξ 3 ). An overview of the first 6 Hermite polynomials is given in Table 3.2. Probabilists Hermite polynomials are monic and orthogonal and they have an easy expression for their norm, h 2 k = He k, He k = 1 2π He k (ξ)he k (ξ) exp ( ξ 2 /2)dξ = k! (3.25) Order Polynomial He (ξ) 1 He 1 (ξ) ξ He 2 (ξ) ξ 2 1 He 3 (ξ) ξ 3 3ξ He 4 (ξ) ξ 4 6ξ He 5 (ξ) ξ 5 1ξ 3 +15ξ Table 3.2: Overview of the 6 lowest order Hermite polynomials. 3.4 Determining expansions coefficients Now that the basis vectors are determined, the only thing that is still unknown in the expansion, Equation (3.15), are the expansion coefficients. The expansion coefficients are calculated using Equation (3.14), which can be written as ( ( ( )... R ξ )Ψ k ξ )p ξ ξ dξ 1 dξ 2... dξ Ndim 1dξ Ndim r k = ( ( ) (3.26) Ψ k ξ ), Ψ k ξ The denominator of this equation is just the norm of the polynomials, which is easy to determine because the exact form of the basis vectors is known. The numerator however requires that an integral is solved in which the exact response, R, plays a role. Obviously the exact form of the response as a function of ξ is not known, therefore this integral can not be solved analytically. To determine the integral, as a first step one-dimensional integrals of this type are approximated using quadratures Quadratures One dimensional integrals of functions can be approximated by a standard quadrature method [4] I (1) f = b a nlev f (ξ) p ξ (ξ) dξ Q (1) lev f = ( f i=1 ξ (i) lev ) w (i) lev (3.27) where f is some function depending on the single variable ξ and ξ (i) lev [a, b] are the quadrature points with associated weights w (i) lev R for a certain quadrature level lev. n lev defines the number of quadratures points in the level lev of the quadrature. The superscript (1) above I and Q indicates the single dimensionality of the integration and quadrature, whereas the superscript (i) indicates the i-th quadrature point and weight contained in the quadrature. A higher quadrature level will have a higher accuracy, however this comes at the cost of having more quadrature points, which means having to do more function evaluations. Equation 3.27 basically comes down to approximating the integral by evaluating the function for different points and taking the weighted sum of the outputs, where the points and weights have been chosen so that the integration error
35 3.4. Determining expansions coefficients 23 is minimized. In this case the function is the dose engine, which means that the dose engine needs to be evaluated for different errors to solve this integral. The quadrature points and weights that are used depend on the quadrature rule that is chosen and the probability function p ξ. Different quadrature rules exist with different properties, although the most important properties are the accuracy and the number of recurring points in each level, called nestedness. A high level of nestedness means that when going to a higher quadrature level, there are a lot of quadrature points that were already calculated in a lower level which are reused. Full nestedness means that each point from a previous level is reused, whereas no nestedness means that for each quadrature level all of the points are different from the previous quadrature level. When evaluating the quadrature points for different levels recursively, that is starting with a quadrature level of 1 and then increasing the level, nestedness can come in handy as this would mean less function evaluations are needed for a higher level. The quadrature points for two different types of quadrature rules are displayed in Figure 3.1 to show different levels of nestedness. Full nestedness can be seen in the Clenshaw-Curtis rule, which has been constructed on a [ 3, 3] interval whereas a limited nestedness is visible in the Gauss-Hermite rule which has only a single reoccurring point. In this case the Clenshaw-Curtis rule would need fewer functions evaluations, however the Gauss-Hermite rule is more accurate. 4 Clenshaw-Curtis Gauss-Hermite Quadrature level ξ (-) Figure 3.1: Clenshaw-Curtis and Gauss-Hermite quadrature rules. The Clenshaw-Curtis quadrature is a fully nested quadrature rule whereas the Gauss-Hermite rule only has 1 nested point, the origin. In this thesis Gaussian quadratures will be used. Gaussian quadratures have the highest polynomial accuracy of all the quadratures rules. For a certain quadrature level Gaussian quadratures can accurately integrate polynomials up to order 4 lev 3 and contain n lev = 2 lev 1 quadrature points. The nestedness of the quadrature is low because only one point, the origin, is included in all of the higher quadrature levels. Because Hermite polynomials are used the specific quadrature rule that is used is the Gauss-Hermite rule. With the quadratures that have just been constructed only single-dimensional integrals can be calculated. However the integral in the numerator of Equation (3.26) is a multi-dimensional integral. Therefore the multi-dimensional equivalent of quadratures will be used which are called cubatures Cubatures A cubature can easily be constructed from a tensorization of quadratures Q (N dim) lev f = ( Q (1) lev 1 Q (1) lev 2 Q (1) lev Ndim ) f (3.28)
36 24 Chapter 3. Polynomial chaos where lev is a multi-index indicating the different quadrature levels that are used for each dimension. Instead of quadrature points, cubatures use cubature points which are the points obtained by taking all possible combinations of the quadrature points of the different dimensions. Assuming that the same quadrature level has been used in all of the directions this will construct a multi-dimensional cube, as seen in Figure 3.2a. It is not necessary for each direction to have the same quadrature level. To indicate the different quadrature levels, a grid-notation is used which describes the different quadrature levels used for each dimension. For example the grid (2, 2, 2,..., 2) indicates that a level of 2 is used in each direction. However the grid (3, 2, 2,..., 2) could also have been used, which would give a higher accuracy in the first dimension. Now the higher accuracy is in the first dimension, but of course it could be placed in any of the dimensions, which is notated as {3, 2, 2,..., 2} which is the collection of all grids which have a single dimension with a level of 3. For example in a 3 dimensional case the collection of grids {3, 2, 2} consists of the grids (3, 2, 2), (2, 3, 2) and (2, 2, 3). Nestedness plays a role again in these grids. Suppose that a (3, 2, 2) and (2, 2, 3) grid are used to solve some integral. It is then possible to first determine the (2, 2, 2) grid, as this will already have some points that are contained in the (3, 2, 2) and (2, 2, 3) grids in the case of the Gauss-Hermite quadratures that are being used. The multi-dimensional integral can now be calculated as b1 b2 a 1 n lev1 a 2... n lev2 i 1=1 i 2=1 bndim a Ndim n levndim i Ndim =1 ( ( ) f ξ )p ξ ξ dξ 1 dξ 2... dξ Ndim ( ) (3.29) f ξ (i1) 1,lev 1, ξ (i2) 2,lev 2,..., ξ (i N dim ) N dim,lev Ndim w (i1) lev 1 w (i2) lev 2... w (i N dim ) lev Ndim In principle the integral of Equation (3.26) can now be solved and the expansion coefficients can be determined. However the current method requires a lot of function evaluations because all combinations of the quadrature points are included in the cubature. This is clearly depicted in figure 3.2a, where the cubature points for a full 4th level grid, using Gauss-Hermite quadratures, in 3 dimensions is shown. To solve the problem of having to do too many function evaluations sparse grids will be used, as can been seen in Figure ξ 3 (-) ξ 3 (-) ξ 2 (-) ξ 2 (-) ξ 1 (-) (a) Full grid, 343 cubature points. ξ 1 (-) (b) Sparse grid, 15 cubature points. Figure 3.2: A full and sparse 4th level grid for a 3 dimensional cubature. The sparse grid has less cubature points which means less function evaluations have to be done Sparse grids Sparse grids are based on the idea that problems are usually dominated by lower order interactions, known as the sparsity of effects principle. Therefore not all grids are equally important, as some
37 3.4. Determining expansions coefficients 25 Grid order N dim Table 3.3: Number of function evaluations needed for different numbers of dimensions and grid orders when using sparse grids based on the Gauss-Hermite rule, if grids are evaluated recursively. of them are used to calculate higher order interactions and these grids are not included in a sparse grid. This means that approximating the integral using sparse grids will give roughly the same accuracy as when a full grid is used, unless high order interactions do play an important role in the problem. In this thesis Smolyak sparse grids will be used [41]. Instead of being based on the quadratures themselves Smolyak sparse grids are based on difference formulas (1) lev f = Q(1) lev f Q(1) lev 1 f (3.3) where by convention Q (1) f =. Introducing the multi-index lev = (lev 1, lev 2,..., lev Ndim ), where lev j indicates the quadrature level in each direction. Then defining lev = N dim j=1 lev j (3.31) the spare cubature formula for a certain level lev can then be written as, Q (N dim) lev f = lev GO+N dim 1 ( (1) lev 1 (1) lev Ndim ) f (3.32) where GO indicates the grid order. A higher grid order means that quadratures with a higher level are included in the cubature, but this will also mean that more points have to be evaluated. Equation (3.29) is still used to solve the integral, but now with different points and weights. Equation (3.32) means that instead of using the same quadrature level in each direction, one starts off with the grid, {1, 1,..., 1} and then divides GO 1 levels among the different directions. For example for a problem with three dimensions a level four cubature will include the grids: {2, 2, 2}, {3, 2, 1} and {4, 1, 1}. The number of points that are used for problems with up to 5 dimensions and up to a grid order 5 can be seen in Table Extended sparse grids Using the sparse grids discussed above means that for a single direction the maximum quadrature level is equal to the chosen grid order. It is also possible to use a higher quadrature level for the single dimensional grid, where a single dimensional grid is a {α, 1, 1,..., 1} grid with α > 1, while keeping the same multi-dimensional grids. In this way it is possible to more accurately determine the single dimensional terms, terms containing only one variable, without adding a lot of cubature points. This can be used when single dimensional terms play an important role in a problem, where otherwise using a higher order grid might be too costly. Suppose a grid is created with grid order 4, this means that the single dimensional grids will be {4, 1, 1,..., 1}. An example of a multi-dimensional grid in this case is {2, 2, 2, 1,..., 1}. By increasing the grid level only for the single dimensions {5, 1, 1,..., 1} grids are included, replacing the {4, 1, 1,..., 1} grids. This means that the {4, 1, 1..., 1} grids are no longer needed and the cubature points associated with those grids do not have to be evaluated. The advantage of this is that the extra number of
38 26 Chapter 3. Polynomial chaos included points is limited, in the case of Gaussian quadratures this will add only 2N dim lev extra quadrature points, where lev is the increase in the single-dimensional quadrature level. Of course only the single-dimensional integrals will benefit from this method. To distinguish between different single- and multi-dimensional grid orders the grid order used for a PCE shall be notated as GOXsY, where X is the grid order in a single dimension and Y is the grid order for the multi-dimensional grids. If the same grid order was used for the singleand multi-dimensional grids this will just be denoted as GOX Hyperbolic trimming Depending on the grid order, polynomial order and dimensionality of the problem for some of the coefficients it is known beforehand that they can not be determined. When the dimensionality of the problem is equal to or larger than the grid order that is used, N dim GO, it is impossible to accurately determine the expansion coefficient for a basis vector for which each single-dimensional polynomial has a polynomial order greater than. Suppose there is a problem with 3 dimensions and a grid order of 3 is chosen to construct the PCE. This means that the maximum multidimensional grid will be of the form {2, 2, 1} and there are no grids with quadrature points in all of the dimensions simultaneously e.g. {2, 2, 2}. As a result it would be impossible to accurately determine the coefficient for a term like φ 1,1 φ 2,1 φ 3,1 (in the case of Hermite polynomials this would be He 1 (ξ 1 )He 1 (ξ 2 )He 1 (ξ 3 ) = ξ 1 ξ 2 ξ 3 ) and actually determining this coefficient would give errors when the PCE is evaluated. Therefore terms are cut out using the q-quasi-norm Equation (3.33), where q is a value between and 1. Basis vectors which satisfy Equation (3.33) will be kept in the expansion, but basis vectors that do not are cut out. Here it can be seen that the maximum polynomial order that can be chosen for a certain grid order is equal to that grid order, because higher order polynomials will get cut out regardless of the value of q. N dim j=1 γ q j 1/q GO (3.33) In the construction of all the PCEs in this work, q is chosen such that all of the basis vectors for which it is known that the coefficient can not be determined are cut out, while trying to keep as many of the other basis vectors as possible. 3.5 Global and local PCE In section 2.2 it was stated that it is important to take into account the different effects of random and systematic errors on the dose distribution. The systematic and random error could of course just be treated as two separate errors and be regarded as different inputs. However this would increase the number of dimensions, as a single error would then require two dimensions, one for the systematic component and one for the random component. However as it turns out the PCE can be constructed for systematic and random errors in a more efficient way. Suppose a systematic error has a distribution and a random error has distribution X N (µ X, σ 2 X) (3.34) Y N (, σ 2 Y ) (3.35) The total, combined error is just the sum of the systematic and random error, so a new distribution can be made, From Equation (3.12) Z can also be written as Z X + Y (3.36)
39 3.5. Global and local PCE 27 Z N (µ X, σ 2 X + σ 2 Y ) (3.37) Now it is possible to draw the total error from this distribution directly instead of sampling from X and Y separately and combining the errors later on. The advantage of this is that when a PCE is constructed instead of X and Y only Z has to be taken into account, which reduces the number of dimensions in the problem. As a result less cubature points will be needed and the construction of the PCE will be faster. A PCE constructed in this way is called a global PCE, which in the case of proton therapy will be referred to as a population PCE. Once the PCE has been constructed for the combined systematic and random error the coefficients of the global PCE can be recalculated to give the PCE one would have obtained if the PCE was constructed for a specific systematic error. This means that the PCE obtained in this way is a PCE of the random errors only, for a specific systematic error. The manipulation of the coefficients is based on the basis vectors that have been used in the expansion, in Appendix A this manipulation is given for the first six Hermite polynomials. The PCE that is constructed in this way is called the local PCE, or in the case of proton therapy a patient PCE. Although all of the coefficients of the local PCE can be calculated in this way this may not always be necessary. For example if the only interest is the mean over the random errors (in proton therapy this means the mean dose over the fractions) given a certain systematic error it is also possible to just calculate the first coefficient of the local PCE, as this is equal to the mean for that systematic error. Determining the mean in this way assumes that for each systematic error an infinite number of random errors are sampled.
40
41 Chapter 4 Dose distributions The first step for using polynomial chaos in proton therapy is constructing a PCE of the dose distribution and verifying whether it is valid to use the PCE. When the dose distribution can be calculated using the PCE, the dose engine is not needed any more and anything that one would like to do with the dose engine can then be done with the PCE. To show the possibilities of a PCE some examples of applications are given at the end of this chapter. 4.1 Constructing a PCE of the dose distribution Cutting out voxels As has been explained in Section the patient is divided into voxels and in each of the voxels the dose is known. The average CT image of the patient consists of somewhere between 1 to 5 million voxels and for each voxel the expansion coefficients of the PCE need to be determined, which will result in a lot of coefficients. If less voxels are included in the PCE there are less coefficients which need to be calculated, resulting in a shorter calculation time. Furthermore when evaluating the PCE, there will be less voxels for which the dose will be calculated and thus the evaluation will also be faster. Moreover the memory requirement, both when constructing and storing the PCE on disk, will be less. Of course there needs to be a valid reason based upon which voxels can be selected to be included in or excluded from the PCE. In this case this is done by looking at the dose in each voxel for the nine standard planning scenarios as described in Section 2.4. For each voxel the maximum dose over the different scenarios is taken, the result of which can be seen in Figure 4.1. As can be seen here the maximum dose over the planning scenarios for more than 95% of the voxels is (almost) Gy. These voxels are therefore not expected to receive any significant dose in other scenarios. Based on this, before the construction of the PCE the dose in the nine planning scenarios is calculated using the exact dose engine. A dose threshold is set and all of the voxels which receive a dose lower than the threshold in all of the scenarios are excluded from the PCE construction. In all of the constructed PCEs in this chapter the dose threshold was set to.1 Gy. When the PCE is evaluated to give a dose distribution, the dose in the voxels which were excluded from the PCE construction is automatically set to Gy Overview of PCE construction The general process for the construction can be seen in the flow diagram of Figure 4.2. Before the PCE is constructed first the input settings need to be given. These settings include the grid order 29
42 3 Chapter 4. Dose distributions Voxels (%) Dose (Gy) Figure 4.1: Cumulative histogram of maximum dose in each voxel over the planning scenarios for a unilateral head and neck patient. The majority of the voxels receive almost no dose in any of the planning scenarios. and polynomial order, the dose threshold, the standard deviation of the errors (the errors are always assumed to be Gaussian distributed) and the treatment plan for which the PCE should be made. The first step in the process is to load these settings. Then the actual calculations begin, first the voxels to be included in the PCE are selected. The next step is to construct the basis vectors and determine the cubature points to be used in the calculation of the PCE coefficients. The cubature points are used to construct the scenarios, which are then passed on to the dose engine to calculate the dose distributions for those scenarios. The resulting dose distributions are used to calculate the expansion coefficients, which completes the construction of the PCE. The PCE can now be used to calculate the dose distribution. Unless otherwise noted the constructed PCE is always a population PCE, that is a PCE that takes into account the total combined setup error and range error as explained in Section 3.5. When evaluating the PCE this will also mean that the total setup error is used. Only when the patient PCE is determined are the systematic and random setup error considered separately. 4.2 Evaluating the PCE It is important that the dose in each voxel as a function of the different shifts is smooth and can be approximated by a polynomial, otherwise the PCE cannot accurately approximate the dose. For a single voxel the dose as a function of the different shifts is depicted in Figure 4.3. This voxel was located in the high-dose CTV. Here both the dose from the dose engine and the PCE are displayed, where the PCE was constructed with GO5s4 and PO5. It can be seen that the dose response is indeed smooth and that the PCE can nicely approximate the exact solution. Once the PCE has been constructed the first thing that can be done is to compare the dose distributions which are calculated by the dose engine and the PCE. The dose distribution for the nominal scenario has been calculated using the dose engine and the PCE, the same slice for both is displayed in Figure 4.4. Here it can be seen that the dose distributions look very similar and no significant difference can be seen between the two. These results are promising as they are a first indication that it is indeed possible to use the PCE instead of the dose engine, thus making it possible to more quickly get the dose distribution.
43 4.3. Validating the expansion 31 Load settings Determine included voxels Determine cubature points Calculate dose in scenarios Calculate expansion coefficients Save data Figure 4.2: Overview of the construction of the PCE. 4.3 Validating the expansion To validate the PCE, Gamma evaluations will be used as explained in 2.5, where in this case the dose distributions determined by an exact and PCE calculation will be compared. However before validating the PCEs for different patients, first a gamma evaluation for different grid orders will be done to determine the grid order that will be used for the construction of the PCE. A lower grid order is preferable as this would require less dose calculations in the construction of the PCE, but a trade-off has to be made between the accuracy and grid order. For each grid order the maximum possible polynomial order was used, as explained in this means that the polynomial order is the same as the grid order. The dose and distance criterion used in all of the gamma evaluations were D =.1 Gy and r = 1 mm respectively. All of the evaluations in this section are done for a total of 681 scenarios which cover an ellipsoid in which 99% of the combined errors lay. This is based on the fact that all of the errors are normally distributed, which means that for a N-dimensional problem (where in this case the dimension is 4), the contour which contains a (1-α)th fraction of the scenarios is given by ( Σ 1 ξ µ) ( ) ξ µ χ 2 N dim (α) (4.1) where χ 2 N dim (α) is the upper (1α)th percentile of the chi-square distribution with N dim degrees of freedom and Σ is the covariance matrix, which in this case is a diagonal matrix [42]. In the case of a 4-dimensional problem this means that for a 99% confidence interval the semi-axis lengths of the ellipsoid are 3.6σ. The evaluated scenarios were created by first equally spacing points along a single dimension, where the two outermost points are placed on the surface of the ellipsoid. Then all possible combinations of the points in the different directions are taken to make a multi-dimensional rectangular grid. The scenarios which were inside of the ellipse are used for the gamma evaluation and all other are discarded, as can be seen in Figure 4.5 for a
44 32 Chapter 4. Dose distributions 7 65 Exact PCE Exact PCE 64 Dose (Gy) 6 55 Dose (Gy) x shift (mm) (a) Dose as a function of shift in x direction y shift (mm) (b) Dose as a function of shift in y-direction Exact PCE Exact PCE Dose (Gy) Dose (Gy) z shift (mm) (c) Dose as a function of shift in z-direction Range shift (%) (d) Dose as a function of shift in range. Figure 4.3: Dependence of dose for different types of shifts for a single voxel, located in the CTV high. Both the exact calculation and the result of the PCE are displayed, which shows that the exact solution can be approximated by the PCE. (a) Dose distribution from dose engine (b) Dose distribution from PCE Figure 4.4: Top view of dose distribution for the nominal scenario for a unilateral head and neck patient. No significant differences can be seen between the exact and PCE calculation.
45 4.3. Validating the expansion 33 3-dimensional problem. 5, 6 and 7 points have been points have been used in a single dimension to determine the scenarios, combining all of the resulting points results in a total of 681 scenarios. Figure 4.5: 99% confidence ellipsoid for a 3-dimensional problem. A rectangular grid is created by taking all possible combinations of the single dimensional points. The orange points are inside the ellipsoid and are used for the evaluations Choosing a grid order For a unilateral head and neck patient the result of the gamma evaluations for different grid orders can be seen in Figure 4.6. Here the gamma evaluations are displayed as a cumulative histogram of the number of scenarios for a certain percentage of accepted voxels. In this way it is possible to quickly see how many of the voxels are accepted in a certain number of the simulated scenarios and vice versa. In the ideal case 1% of the voxels is accepted in 1% of the scenarios, which would mean that the PCE is a perfect replacement for the dose engine, but of course this will not be the case. The first thing that can be noticed is that a grid order of 2 performs very poorly, only 5% of the voxels is accepted in 7% of the scenarios, which is of course unacceptable. But this is not unexpected, as a second order grid can not take into account any multidimensional terms, since the maximum grids that are used are {2, 1, 1, 1} grids. This means that there are no cubature points for multiple dimensions simultaneously. Then a huge leap in accuracy is visible when going to a grid order of 3, because now multi dimensional terms are included in the PCE. Although there is no exact definition of when the accuracy is acceptable, in this case only 8% of the voxels is being accepted in 8% of the scenarios, which was not deemed sufficient In the end a GO5s4 was chosen. Although the accuracy of a fourth order grid was already good, the cost of constructing a GO5s4 PCE is limited compared to a GO4 because only eight additional scenarios have to be calculated, while the increased accuracy is still significant. This means that when constructing a PCE 29 scenarios have to be calculated by the dose engine. With the GO5s4 a q of.861 was used, which resulted in 73 basis vectors being included Gamma evaluations Now that a grid order is chosen, the accuracy of the PCEs is verified for multiple patients.
46 34 Chapter 4. Dose distributions Scenarios (%) GO2PO2 GO3PO3 GO4PO4 GO5s4PO Accepted voxels (%) Figure 4.6: Gamma evaluations for a unilateral head and neck cancer patient for different grid orders. Based on these evaluations a GO5s4 was used for the construction of the PCEs for different patients. Head and neck patients For all six of the head and neck patients a gamma evaluation was done for a non-robust plan. The results of the gamma evaluation for can be seen in Figure Scenarios (%) HN patient 1 HN patient 2 HN patient3 HN patient 4 HN patient 5 HN patient Accepted voxels (%) Figure 4.7: Gamma evaluation for a non-robust plan for different head and neck patients for a GO5s4PO5 PCE. Gamma evaluations were done with D =.1Gy and r = 1 mm. The evaluation results for the different patients are similar and are acceptable for all patients. From these evaluations it can be seen that the difference between the different gamma evaluations is small and that for each patient the result is acceptable. In each patient 8% of the voxels were accepted in all of the scenarios and even for the worst performing patient 9% of the voxels are accepted in 95% of the scenarios. From this it can be concluded that for head and neck patients the accuracy of the PCE is acceptable and that the PCE can be used instead of the dose engine. It was also evaluated where the voxels which were not accepted are located. For a unilateral patient for the scenario with the lowest fraction of accepted voxels a slice with the gamma values in the voxels is depicted in Figure 4.8. This worst case scenario was the maximum shift in the z-direction, that is the scenario which did not have a setup error in the x or y direction and no range error, but the z-shift was located on the 99% ellipsoid. Therefore it is one of the most extreme scenarios that were taken into account in the evaluation, and it is not surprising that this scenario has a low number of accepted voxels. The depicted slice was the slice with the highest gamma values (and thus the worst slice) in the CTV high, for which it is important to get a good
47 4.3. Validating the expansion 35 approximation as it is an important structure. As can be seen most voxels of the CTV are not accepted in this slice. However when going to a different slice the gamma values rapidly become better. Thus although the shown slice seems unacceptable, keeping in mind that this is the worst slice for the worst case scenario, overall the PCE still is acceptable. Furthermore it can be seen that most of the voxels which were not accepted are outside structures and for these voxels it is more acceptable that they have failed the gamma evaluation. Figure 4.8: Gamma values for a unilateral patient for the scenario with the least amount of accepted voxels, the color bar indicates the gamma value. Only the non-accepted voxels are displayed. Prostate patients For the five prostate patients the grid order that was used was also based on the calculation for the head and neck patient, so again a GO5s4 was used. The result for a non-robust plan for the different prostate patients can be seen in Figure 4.9. Here it is directly clear that for the prostate patients the accuracy is a lot less than it was for the head and neck patients. Now 9% of the voxels is accepted in only 45% of the scenarios instead of 95% of the scenarios for the head and neck patients. Unfortunately no definitive cause for this decline in accuracy was found, only two probable reasons. First of all it might have to do with the shape of the CTV. Due to the shape of a prostate tumour compared to a head and neck tumour there are relatively more voxels at the edge of the CTV. In these voxels a sharp dose response is expected, as the dose gradient at the edge of the CTV is large. These sharp responses might be harder to approximate with the PCE and thus results in a lower accuracy. Another reason might have to do with the prescription dose of the prostate patient. Whereas this was 66 Gy in the head and neck case it is now 74 Gy, which may result in larger absolute differences and of course this means a worse gamma evaluation as the dose criterion was unchanged. For a prostate patient the gamma values in the voxels for the worst slice of the worst scenario are shown in Figure 4.1. In this case the worst scenario was a combination of the most extreme points in the y and z direction and the range shift. From this figure it can also be seen that the accuracy of the PCE is lower than in the case of the head and neck patients as the gamma values are very high. It is interesting to see that a lot of the failed voxels are on the same line, probably because the dose they receive all comes from the same pencil beam. To improve the accuracy of the PCE in the case of these prostate patient a PCE was constructed without taking into account errors in the x-direction. This was done because for these patients the two beam angles were opposite of each other and parallel to the x-direction. As a result a shift in the x-direction does not have an influence on the dose, as this would only shorten or lengthen the distance that the protons travel through the air and this will practically have no effect on the proton range. Now the accuracy of the PCE might become better because there is one less dimension, making it easier to accurately determine the multi dimensional dependence.
48 36 Chapter 4. Dose distributions Prostate 1 Prostate 2 Prostate 3 Prostate 4 Prostate 5 6 Scenarios (%) Accepted voxels (%) Figure 4.9: Gamma evaluation for a non-robust plan for different prostate patients for a GO5s4PO5 PCE. Gamma evaluations were done with D =.1Gy and r = 1 mm. The results are worse than for the head and neck patients. Figure 4.1: Gamma values for a prostate patient for the scenario with the least amount of accepted voxels, the color bar indicates the gamma value. Only the non-accepted voxels are displayed.
49 4.3. Validating the expansion 37 The PCE that was constructed in this way was also validated using a gamma evaluation. The same 681 scenarios as in the previous gamma evaluation were used, which means that scenarios with an x-shift were also included. However when the PCE was evaluated for those scenarios nothing was done with the x-shift. This was done for only one patient, prostate patient 1 in the previous figures, the result for which can be seen in Figure Scenarios (%) Accepted voxels (%) Figure 4.11: Gamma evaluation for a non-robust plan for a single prostate patient for a GO5s4PO5 PCE where no dependence on the x-shift was included. Gamma evaluations were done with D =.1Gy and r = 1 mm. The accuracy has increased compared to the normal PCE. The accuracy of the PCE has increased a little, although the results for the head and neck patients are still better. Leaving out the x-dependence is a valid thing to do in this case, but unfortunately when the beams are not opposite to each other this is not a valid solution. To account for this a treatment plan was made where the beams were not opposite to each other. In this case a GO5s4 and a GO5 are used, shown in Figure The GO5 improves the accuracy of the PCE, although it is still worse than in the case of a head and neck patient, but it will also require many more calculations. With GO5s4 29 scenarios needed to be calculated, but in this case a total of 681 scenarios needed to be calculated (coincidentally this is the same as the number of scenarios in the gamma evaluation but there is no relation between them). The question remains whether in this case constructing the PCE is worth it as it requires so many calculations of the exact dose engine Scenarios (%) GO5s4PO5 GO5PO Accepted voxels (%) Figure 4.12: Gamma evaluation for a non-robust plan for a single prostate patient for a GO5s4PO5 and GO5PO5 PCE for the case where the beams were not parallel. Gamma evaluations were done with D =.1Gy and r = 1 mm. The accuracy of the PCE has improved for the fifth order grid, but required a lot more calculations of the exact dose engine.
50 38 Chapter 4. Dose distributions Absolute dose difference For completeness the absolute dose difference between the PCE and exact calculation is determined. The same 681 scenarios were used as the ones used for the gamma evaluations, but now for each scenario the D 2 of the dose difference, D 2, was determined. 98% of the voxels have a smaller difference than the D 2. The result of this for the evaluated head and neck patients can be seen in Figure Scenarios (%) HN patient 1 HN patient 2 HN patient 3 HN patient 4 HN patient 5 HN patient D 2 (Gy) Figure 4.13: Cumulative histogram of the D 2 between exact and PCE calculation for head and neck patients for a total of 681 scenarios which covered 99% of the scenarios. From this figure it can be seen that in more than 9% of the scenarios the D 2 of the dose difference is below 2 Gy. Considering that this is a direct comparison it is an acceptable difference. For the prostate patients the same evaluation was done, which can be seen in Figure This evaluation was done for the PCE of the original treatment setup, that is the PCE which did have x-dependence but where the beams were opposite of each other. Again it can be seen that for the prostate patients the accuracy of the PCE is lower than for the head and neck patients. Now for 9% of the scenarios the D 2 is 4 Gy instead of 2 Gy for the worst patient Scenarios (%) Prostate 1 Prostate 2 Prostate 3 Prostate 4 Prostate D 2 (Gy) Figure 4.14: Cumulative histogram of the D 2 between exact and PCE calculation for a prostate patients for a total of 681 scenarios which covered 99% of the scenarios. More types of evaluations of the accuracy of the PCE are shown in Appendix B. There robust
51 4.4. Timing results 39 plans are also evaluated. 4.4 Timing results The goal of using the PCE was to reduce the time needed to simulate patient treatments and in this way get information about the effects of different uncertainties faster. Therefore it is important to look at the actual reduction in time that is achieved by using a PCE. The construction of all of the PCEs was done on 4 Intel Xeon E5-269 CPUs with a clock speed of 2.9 Ghz using 4 Gb of RAM. The time needed to evaluate the PCE and the dose engine was based on the calculation time for the nine standard planing scenarios. This was done because the dose engine is faster when multiple scenarios are calculated at once instead of separately. Therefore this is a more fair comparison than just using a single scenario. The results of the timing are summarized in Table 4.1. Patient PCE construction time Planning scenarios calculation time PCE Exact Head and neck 1 67 minutes 3.4 s 366 s Head and neck 2 82 minutes 4.7 s 5 s Head and neck 3 83 minutes 4.7 s 556 s Head and neck 4 53 minutes 2.5 s 31 s Head and neck 5 72 minutes 3.5 s 351 s Head and neck 6 11 minutes 7.3 s 823 s Prostate 1 33 minutes 4.6 s 324 s Prostate 2 5 minutes 5.8 s 434 s Prostate 3 8 minutes 6.7 s 412 s Prostate 4 55 minutes 7.1 s 531 s Prostate 5 58 minutes 6.9 s 454 s Table 4.1: Overview of time needed to construct and evaluate a GO5s4 PCE for different patients. The calculation time needed for the nine planning scenarios is compared between the dose engine and the PCE. The construction time differed a bit per patient, but on average the construction time for a head and neck patient was 8 minutes and 55 minutes for the prostate patients. The evaluation time was reduced by approximately a factor 1 for all of the patients, which means that the goal of speeding up the dose calculation is achieved. 4.5 Applications The accuracy of the PCE is now verified, but up until this point the fact that systematic and random errors can be simulated as described in Section 3.5 has not yet been used. Since the PCE was constructed for the combined systematic and random setup error, it is possible to create the patient PCE from the population PCE. When one only wants to know the mean dose over a treatment this can be done by only determining the first coefficient of the patient PCE instead of all of the coefficients, as the first coefficient is equal to the mean, assuming infinite fractions. Furthermore, by only selecting a certain structure for which to calculate the mean dose the number of coefficients of the patient PCE can be further reduced, decreasing the calculation time. Even though 29 scenarios are needed to construct the PCE the added advantage is now that the effect of systematic errors can be easily taken into account. Furthermore all of the information that the dose engine can provide can now also be obtained from the PCE, which is not the case for MC sampling. So all in all constructing the PCE is worth the extra construction time. To show the clinical relevance of this some applications using the possibilities of the PCE are shown in this section.
52 4 Chapter 4. Dose distributions DPH The PCE is very useful for creating dose population histograms, as they require systematic errors to be taken into account. By simulating different systematic errors using the PCE it is possible to quickly construct a DPH, which could for example be used to compare different plans. In Figure 4.15 a non-robust plan, a (3,,)-plan and (5,,)-plan are compared by looking at the D 98 of the CTV high, which clearly shows the improvement in CTV coverage when using a larger robustness Population (%) Non robust plan (3,,) plan (5,,) plan D 98 (%) Figure 4.15: Dose population histogram for plan with different robustness settings, D 98 is expressed as a percentage of the prescribed dose. Robustness for different plans can be evaluated in this way Fractionation Using the PCE it is possible to simulate the effect of different numbers of fractions used for a treatment. Normally infinite fractions are assumed because it is then possible to get the mean dose over a treatment for a certain systematic error directly from the coefficients of the expansion. However it is also possible to simulate different numbers of fractions by sampling different systematic errors and for each systematic error creating a patient PCE, which is then used to simulate a certain number of fractions by sampling different random errors to determine the mean dose over the fractions. This has been done to compare treatments with 1, 3 and infinite fractions, the result of which can be seen in Figure In this figure the DPH of the D 98 of the CTV high is shown. It can be seen that increasing the number of fractions will result in a better CTV coverage for the population. This can be expected because when using fractionation the different random errors might cancel out. The difference between 3 and infinite fractions is small, which means that using the PCE for infinite fractions comes close to actually simulating a treatment in which 3 fractions are given Treatment parameters Based on the simulated dose over a treatment it is possible to construct different treatment parameters. For example a DVH has been simulated for a nominal scenario, as seen in Figure The DVH from the PCE and from the exact calculation overlap nicely, as can be expected since this is based on the dose calculated by the PCE and the accuracy of that was already verified. It is now possible to very quickly determine the DVH for different scenarios, to get an idea of the spread. Another parameter that is interesting is the V 95 of the CTV. The V 95 of the high-dose CTV is given as a function of shifts in the x- and y-direction in Figure 4.18 for a (3,3,)-robust plan. In this figure the plan robustness can be seen as there is a plateau where the V 95 is almost
53 4.5. Applications Population (%) fraction 3 fractions In nite fractions D 98 (%) Figure 4.16: Dose population histogram for treatments with 1, 3 and infinite fractions. Increasing the number of fractions results in a higher CTV coverage. 1 Volume (%) CTV high CTV low Cord Parotid PCE Dose (Gy) Figure 4.17: DVH for different structures determined by an exact calculation and the PCE for the nominal scenario, for a unilateral head and neck patient.
54 42 Chapter 4. Dose distributions 1%. When the errors get too large the V 95 falls off very quickly because those errors were not accounted for during the optimization V 95 (%) y shift (mm) x shift (mm) Figure 4.18: V 95 as function of shifts in the x and y direction for a (3,3,)-robust plan. Because the PCE can be used to simulate the dose it is possible to obtain whichever treatment parameter one is interested in Underdosage Using the PCE to calculate the mean dose over a treatment it is possible to see where in the patient the dose in the CTV is insufficient. In order to do this the mean dose over a treatment was calculated for a total of 5 systematic errors, where the dose in the CTV high was considered for a (3,,)-plan. For each sample it was determined whether the dose in a voxel was sufficient or not, where a dose less than 98% of the prescribed dose was deemed insufficient. By counting the number of scenarios in which a voxel had an insufficient dose Figure 4.19 was made. Here two slices are displayed, one at the edge (along the z-direction) of the CTV and one in the middle of the CTV. It can be seen that the edge slice is more underdosed than the slice in the middle of the CTV. This could be expected of course, because the edges of the CTV are more sensitive to a displaced dose since there is a higher dose gradient there. The same effect is visible in the middle slice of the CTV as the edge of the CTV in that slice is also underdosed. These kinds of figures can be used to show the effects of uncertainty on the dose distribution for a certain plan. For example if the underdosage would be in the middle of the CTV that would be less acceptable than in this case where it is at the edge. The same thing could be done for the CTV low and one might also consider looking at OARs and determine the overdosage there.
55 4.5. Applications 43 (a) Slice towards the exterior of the CTV (b) Slice in the middle of the CTV Figure 4.19: Underdosage in the voxels of the high dose CTV. The color bar indicates for which percentage of the simulated scenarios the dose was less than 98% of the prescribed dose in that voxel..
56
57 Chapter 5 Treatment parameters In the previous chapter some applications of the PCE were discussed, including the simulation of different treatment parameters. However to obtain a treatment parameter the PCE still needs to be sampled for different systematic errors to obtain the mean dose over a treatment and determine the parameter based on this. As explained in Section 2.3 the dose parameters are a function of the mean dose over the fractions, λ(σ) = f(e σ [D(Σ, σ)]) (5.1) where λ indicates some treatment parameter, Σ indicates a systematic error, σ indicates a random error and E σ [ ] indicates the mean dose over the fractions (which means over the random errors). In the previous chapter a population PCE was made of the dose, which in this chapter will be referred to as the dose PCE, were both systematic and random errors were considered which can be used to calculate D(Σ, σ). In Section 3.5 it was shown that it is possible to quickly obtain the mean dose over the fractions, E σ [D(Σ, σ)], if infinite fractions are assumed. However this means that to determine the value of a parameter, first E σ [D(Σ, σ)] needs to be determined every time. If a PCE could be made of λ(σ) directly this means that the parameter for a certain systematic error can be determined directly using this new PCE, without the need for the intermediate step of determining the mean dose. Another disadvantage of the dose PCE is that the bandwidth of a parameter can not be determined directly from the dose PCE. Suppose that a DVH is constructed, one might then be interested in the standard deviation of the DVH to determine what the spread of the DVH will be over a population, as a different DVH is associated with each systematic error. This can be done by looking at the bandwidth of the DVH, determined by its standard deviation [43]. The coefficients of the dose PCE directly give the standard deviation of the dose, as explained in Section 3.3.1, but this does not have a direct relation to the standard deviation of the dose parameter. Of course the bandwidth of the parameter could be constructed by sampling the dose PCE for different systematic errors, but if a PCE of a parameter is constructed it is possible to directly obtain the standard deviation of the parameter from the coefficients of the PCE. Therefore in this chapter the PCE of a specific parameter will be considered, henceforward referred to as a parameter PCE or λ-pce. A quick comparison between the possibilities of the dose PCE and λ-pce is given in Table 5.1. Here it can be seen that in principle it is possible to obtain all of the information that one would like to have using the dose PCE. This is logical as the dose PCE is actually a meta-model of the dose engine itself, which contains all possible information. The λ-pce contains less information as it can only determine parameters, calculating a dose distribution is not possible. However it is expected that evaluating the λ-pce is faster than sampling the dose PCE. 45
58 46 Chapter 5. Treatment parameters Calculate dose distribution Calculate parameter Dose PCE yes yes, by first calculating E σ [D(Σ, σ)] Determine parameter bandwidth yes, by sampling the PCE Parameter PCE no yes, evaluate PCE yes, directly from coefficients Table 5.1: Comparison of possibilities of dose PCE and parameter PCE. Although the λ-pce might seem very similar to the direct route discussed in Chapter 1 there is a important difference between the two. In the case of the direct route systematic errors were not taken into account, only random errors. The λ-pce on the other hand determines the parameters as a function of the systematic errors, no random errors are present anymore as the mean dose over the random errors was taken. 5.1 Constructing a parameter PCE When constructing the dose PCE the dose engine was used to determine the dose distributions for the quadrature points, this was then used to calculate the coefficients of the expansion. Here the dose engine was seen as the exact method and the PCE as an approximation. In this case the mean dose over the fractions is needed, which can quickly be calculated using the dose PCE. Therefore in this case the dose PCE is seen as the exact solution and the λ-pce is seen as the approximation. Using the dose engine itself is almost impossible in this case, as it is very time consuming to calculate the effect of fractions using the dose engine. An overview of the construction of the λ-pce is given in Figure 5.1. The first part of the construction is the same as for the dose engine, the settings are loaded and the cubature points are determined. However after this instead of using the cubature points as scenarios for the dose engine it will now be used to determine E σ [D(Σ, σ)] using the population dose PCE. This means that the cubature points are now seen as the systematic errors and for each of them the first coefficient of the patient PCE is calculated to determine the mean dose over the treatment. Based on the mean dose, the value of the parameter is determined, and the coefficients of the expansion can be calculated λ-pce of the DVH The first λ-pce that was created was for the DVH of the CTV high for a unilateral head and neck patient. The GO5s4PO5 population PCE from the previous chapter was used in the construction of the λ-pce and it was also sampled for 1 systematic errors to determine the mean and bandwidth of the DVH. The λ-pce was made by binning the DVH horizontally, i.e. by actually determining D α for different α, where 5 bins were used. The results of this can be seen in Figure 5.2, where a GO4PO4 λ-pce has been constructed. The mean and bandwidth obtained from sampling the dose PCE are regarded as the exact solution. It can be seen that the λ-pce very closely approximates the mean and bandwidth from the dose PCE. Constructing the λ-pce took only 4 seconds, the sampling of the PCE took 13 seconds. So although the sampling of the dose PCE is not very slow, the benefit of not having to do any sampling still remains. Using the λ-pce a physician could very quickly, in less than one hundredth of a second, see the DVH for a error scenario, where this could take up to a second using the dose PCE.
59 5.1. Constructing a parameter PCE 47 Load settings Determine cubature points Calculate E σ [D(Σ, σ)] using dose PCE Calculate parameter Calculate coefficients Save data Figure 5.1: Overview of the construction of the λ-pce Volume (%) dose PCE mean λ PCE mean dose PCE ± 2σ λ PCE ± 2σ Dose (Gy) Figure 5.2: DVH mean and bandwidth obtained by sampling the dose PCE and by constructing a λ-pce. The results from the dose PCE are in this case seen as the exact solution.
60 48 Chapter 5. Treatment parameters λ-pce of the V 95 A λ-pce was also made of the V 95, which can be seen in Figure 5.3, where the V 95 is displayed as a function of the systematic x-shift. The V 95 obtained by determining the mean dose from the dose PCE, a GO7PO7 λ-pce and a GO1PO1 λ-pce are depicted. Once again the V 95 obtained using the dose PCE is seen as the exact solution. As can be seen the V 95 is hard to approximate, as the GO7 λ-pce performs very poorly. From a polynomial fit of the data it was seen that at least a 1th order polynomial is needed to get a good fit, therefore the GO1PO1 PCE was also constructed. Figure 5.3 shows that a 1th order grid is a good approximation, however it required evaluations, at which point it is faster to actually just sample the dose PCE. Even with this large amount of evaluations the λ-pce still deviates from the exact solution. To solve the problem of the high grid order that is needed multi-element polynomial chaos is used V 95 (%) Dose PCE GO7PO7 λ PCE GO1PO1 λ PCE Systematic x shift (mm) Figure 5.3: V 95 as a function of the system x-shift, determined using the GO5s4PO5 dose PCE and a GO7PO7 and GO1PO1 λ-pce. 5.2 Multi-element polynomial chaos Multi-element polynomial chaos (ME-PC) is based on the idea that instead of making a PCE over the whole range of a variable, which in the case of a Gaussian variable theoretically means from to, the range can be divided into different sections. In each of these sections a PCE is then made, which can all be evaluated individually and by combining the results the whole range of a variable can be covered. This means that a regular Gaussian distribution can not be used anymore, as it spans the whole range, therefore truncated Gaussian distributions will be used. A regular and truncated Gaussian distribution are compared in Figure 5.4, where the truncated Gaussian has been truncated to the range from 2σ to 2σ. Because the area under the PDF still has to remain 1 the truncated Gaussian has been rescaled, which gives the truncated Gaussian in the range from a to b as p (a,b) p ξ ξ = b p ξdξ a p ξdξ Because the truncated Gaussian is not in the Wiener-Askey scheme, the basis vectors need to be determined in some other way. The basis vectors for an arbitrary PDF can be constructed from a recurrence relation [44] (5.2)
61 5.2. Multi-element polynomial chaos Normal Gaussian Truncated Gaussian.2.15 p ξ (-) σ -2 σ -σ σ 2σ 3σ ξ (-) Figure 5.4: Comparison of a regular Gaussian distribution and a truncated Gaussian distribution. φ i+1 (ξ) = (ξ α i )φ i (ξ) β i φ i 1 (ξ) φ = 1 φ 1 = (5.3) which automatically construct orthogonal, monic polynomials. The values of α i and β i can be determined using the Stieltjes procedure, α i = ξφ i, φ i φ i φ i β = φ, φ β i = φ i, φ i φ i 1, φ i 1 (5.4) Of course this also means that different quadrature points and weights need to be used. This once again depends on the quadrature rule chosen, here Gaussian quadrature rule is used again. The quadrature points are then the zeros of the polynomials constructed in Equation (5.3) and the weights can be determined as b w (i) lev = a ω(ξ)φ n 1(ξ) 2 dξ φ lev (ξ(i) lev )φ lev 1(ξ (i) lev ) (5.5) where ω is the weight function, φ is the one-dimensional polynomial and n is the quadrature level. In this case the weight function is chosen the same as the weight function of the Gauss- Hermite rule. Although this may not be the optimal weight function anymore, because the distribution of the variable is now truncated and not a perfect Gaussian, it is expected to give good results because the distributions are still very similar to a Gaussian. Constructing a PCE based on an arbitrary PDF in this way is referred to as arbitrary polynomial chaos (apc) [45]. Multi-element polynomial chaos will only be used to construct the λ-pce. The dose PCE is not constructed using ME-PC, as it is already constructed and seen as the exact solution in this case. The range of a variable will be split up into three regions; [, 2σ],[ 2σ, 2σ] and [2σ, ]. For each of these regions a truncated Gaussian will be used with corresponding basis vectors, quadrature points and quadrature weights. Implementing multi-element polynomial chaos in multiple dimensions proved too difficult because of time constraints, therefore a ME-PCE is only constructed for a single dimension, the systematic x-shift. A ME-PCE was made of the V 95 that was shown in Figure 5.3. A 4th order grid was used in each of the three regions resulting in a total of 3 13 = 39 points. In Figure 5.5 the V 95 obtained
62 5 Chapter 5. Treatment parameters using the dose population PCE, which is regarded as the exact solution, the previously constructed λ-pce, which took into account all of the dimensions, a λ-pce of only the systematic x-shift and the multi-element λ-pce are displayed. The λ-pce of only the systematic x-shift was included to ensure that the improvement of the multi-element PCE was actually due to using multiple regions and not just because a PCE was made of a single dimension. For this one-dimensional λ-pce a 7th order grid was used, which meant 43 quadrature points were needed, more than in the multi-element case. As can be seen the 1D λ-pce has improved from the GO1PO1 λ-pce which included all of the errors (x-shift,y-shift,z-shift and range). However the multi-element λ-pce seems to be the best approximation while it required the least amount of quadrature points. Therefore it can solve the problem of the inaccuracy of the λ-pce while keeping the number of quadrature points reasonable V 95 (%) Dose PCE GO1PO1 λ PCE GO7PO7 1D λ PCE GO4PO4 1D ME λ-pce Systematic x shift (mm) Figure 5.5: V 95 as a function of the systematic x-shift based on different PCEs. Results of a GO5s4PO5 dose PCE, GO1PO1 λ-pce, GO7PO7 1D λ-pce and GO4PO4 1D ME-λ-PCE are shown. The ME-PCE shows the best approximation of the exact solution.
63 Chapter 6 Article: Robustness recipes 6.1 Introduction Intensity-modulated proton therapy (IMPT) uses proton pencil beams whose intensities are individually optimized, which potentially results in an improved sparing of organs at risk (OAR) compared to intensity-modulated radio therapy (IMRT) [12]. However, IMPT is highly susceptible to uncertainties occurring during treatment which results in a difference between the planned and delivered dose [11, 17, 2]. These uncertainties stem from inaccuracies in the patient setup, which are characterized by a systematic and random component, and from uncertainties in the conversion of Hounsfield units to proton stopping power, known as range errors [21]. When constructing a robust treatment plan using minimax optimization these inaccuracies are taken into account by optimizing the dose for a limited number of patient positions and range errors while optimizing the worst-case scenario [27]. However, it is currently unknown what magnitude of the errors should be included in the robust optimization to reach an adequate coverage of the clinical target volume (CTV). In IMRT, margin recipes are often used to calculate the CTV to planning target volume (PTV) margin needed to achieve a specified CTV coverage when dealing with certain systematic and random setup errors [24]. Because the concept of a PTV is not applicable in proton therapy [46] this recipe cannot be used, thus a robustness recipe is needed to determine the error scenarios that need to be included in the optimization, given a priori known error distributions. In this study we derived robustness recipes for one unilateral and one bilateral IMPT head and neck cancer patient. Different robustness settings were evaluated through extensive simulations by systematically testing the CTV coverage for different combinations of systematic and random set-up and range errors. The acceptability of the CTV coverage was based on the fraction of the population which received a D 98 of 95%. This fraction was determined by sampling a polynomial chaos expansion to simulate a fractionated treatment to construct a DVH. The results of the simulations were verified by generating robust treatment plans for six unilateral and six bilateral head and neck cancer patients with the derived robustness settings, subsequently checking the CTV coverage for these plans. 6.2 Methods and materials Patient data and dose prescriptions In this study we used the data of one bilateral and one unilateral oropharyngeal cancer patient to construct the robustness recipes and six unilateral and six bilateral patients were used as 51
64 52 Chapter 6. Article: Robustness recipes verification. A dose of 66 Gy was prescribed to the high-dose CTV and a dose of 54 Gy to the low-dose CTV, to be delivered in 3 fractions [13]. During the robust optimization at least 98% of the CTV should receive 95% of the prescribed dose (V 95 98%) in all of the error scenarios. Furthermore a maximum of 2% of the CTV was allowed to receive more than 17% of the prescribed dose (V 17 2%). Three beam directions with angles of 6, 18 and 3 degrees were used Treatment planning Robust treatment plans were made using Erasmus-iCycle [25], a fully automated treatment planning system that was developed in-house. The Erasmus-iCycle algorithm uses prioritized multi-criteria optimization. Instead of using a single weighted-sum objective function it optimizes the different objectives one-by-one given the priorities defined by the user in the wish-list. The wish-list used in this work can be seen in table 6.1. Constraints can also be defined, which have to be met during the optimization. To select and optimize the pencil beams during optimization resampling was used. [26]. First, candidate pencil beams are randomly sampled from a very fine grid. Then the multi-criteria optimization is performed and at the end of the iteration the pencil beams with a low contribution are excluded from the next iteration. This process is then repeated for each optimization iteration. The optimization was stopped when the minimum objective change was less than 3%. Proton energies that could be used ranged from 7 to 23 MeV and corresponding pencil beam widths ranged from 7 to 3 mm sigma (in-air at the isocenter), respectively. A range shifter of 75 mm could be used when a superficial target needed to be irradiated. Constraints Structure Type Limit Robust CTV high Minimum Gy yes CTV intermediate Minimum Gy yes CTV low Minimum Gy yes Objectives Priority Structure Type Goal Robust 1 CTV high Maximum Gy yes 1 CTV intermediate Maximum Gy yes 1 CTV low Maximum Gy yes 3 Parotid Mean Gy yes 4 Submandibular glands Mean Gy yes 5 Cord Maximum 2 Gy yes 5 Brain stem Maximum 2 Gy yes 6 Larynx Mean Gy yes 6 Oral cavity Mean Gy yes 7 Swallowing muscles Mean Gy yes Table 6.1: Wish-list describing the dose prescriptions used in this study. The order in which the objectives were optimized is indicated by the priority where a lower priority number means a higher priority. The CTV intermediate is a 1 mm transition region between the high-dose and low-dose CTV. The CTV-low consists of the low-dose CTV excluding the transition region. To account for setup and range errors, which are defined by the standard deviation (denoted by sigma), of their distribution, a minimax approach was used [27]. When using the minimax method several error scenarios are included in the optimization and the worst-case value of each constraint and objective is optimized. The included scenarios consisted of the nominal scenario, a positive and negative setup error along the three different directions (resulting in six scenarios),
65 6.2. Methods and materials 53 referred to as setup robustness, and a positive and negative range error (resulting in two scenarios), referred to as range robustness. This gives a total of nine scenarios which were included in the optimization. Setup errors were simulated by laterally shifting the pencil beams and range errors were simulated by scaling the values of the CT image Treatment simulations To quantify the CTV coverage for a treatment plan, dose population histograms (DPHs) have been constructed for different combinations of systematic and random setup errors and range errors. A DPH shows the fraction of the population which has a certain CTV coverage, in this case expressed as the D 98 of the CTV. An example of a DPH can be seen in figure 6.1, showing that 7% of the population receives a D 98 of 98%, which is not considered to be a adequate coverage. To simulate the effects of both systematic and random setup errors, as well as range errors, polynomial chaos expansions (PCEs) were used. The PCE is a meta-model of the dose engine and can be used to very quickly simulate the effects of uncertainties. Setup and range error were assumed to have a Gaussian distribution. and the construction of the PCE was done accordingly. Once the PCE was built it was sampled for 1. different systematic errors. For each sample the mean dose over the treatment was calculated assuming an infinite number of fractions, from which the D 98 was determined, and finally the DPH was constructed Population (%) D 98 (%) Figure 6.1: Example of a dose population histogram. The D 98 of the CTV high was determined for different systematic errors to simulate a population Study design First, we determined which range robustness was needed to get an adequate CTV coverage in the case of 1% and 2% range error, for a % range error it is assumed that no robustness is needed. An acceptable tumor coverage was defined from the DPH as 98% of the CTV (both the low-dose and high-dose CTV) receiving a dose of 95% of the prescribed dose, i.e. D 98 = 95% (or equivalently V 95 = 98%) for at least 98% of the population. The range robustness was increased in steps of 1% until this CTV coverage was obtained. Using the obtained range robustness plans were made for the unilateral and bilateral patient with a setup robustness of 2, 3, 4 and 5 mm. Subsequently the robustness of these plans was evaluated. For the robustness evaluation seven random errors with standard deviations of to 3 mm with steps of.5 mm were considered. For each of these random errors we determined the maximum systematic setup error that would still give an acceptable CTV coverage. An overview of the method to find the maximum systematic error for a specific robustness setting, random setup error and range error can be found in figure 6.2. We first set an initial guess for the systematic setup error. We then simulated a treatment and looked at the resulting DPH. When the D 98
66 54 Chapter 6. Article: Robustness recipes was 95% for at least 98% of the population the systematic error was increased, if it was less than 98% of the population the systematic error was decreased. The minimum change of the systematic error was.5 mm. At some point the previous systematic error did pass the coverage criterion, but the increased error did not. In that case the previous systematic error was taken as the maximum systematic error that could be handled. Make plan for robustness setting Set initial guess for systematic setup error Construct PCE for plan and errors Decrease systematic error Sample PCE to construct DPH No Previous systematic error did pass? No D 98 = 95% for at least 98% of population? Yes Increase systematic error Yes Previous system error is maximum possible systematic error Figure 6.2: Overview of method to determine the maximum systematic error that can be handled by a certain plan to still give an acceptable CTV coverage. It would also be possible to construct the robustness recipe by looking at the robustness needed to handle a certain error instead of searching for the error that can be handled by a certain robustness. However it is much more time consuming to construct a treatment plan than constructing a PCE for different errors and therefore the latter approach was chosen. The obtained data was verified by looking at a specific combination of errors for a total of 12 patients, including the two patients that were used to obtain the data. For each patient we considered a systematic and random setup error of 1.5 mm and a range error of % and 2%. Since the robustness recipes were generated for discrete values of the setup robustness settings, no line goes through the point of a 1.5 mm systematic and random setup error. The needed systematic setup robustness was therefore determined by linearly interpolating between
67 6.3. Results 55 two known, consecutive robustness settings for a 1.5 mm random setup error, where robustness setting could handle an systematic setup error larger than 1.5 mm and the other one lower than 1.5 mm. The range robustness obtained for the earlier patients was used for the new patients as well. A treatment plan was made for the patients based on those robustness settings and once again a PCE and DPH were constructed from which we determined the fraction of the population that received a D 98 of 95%. Based on the the combinations of errors that can be handled with a given robustness settings we made a robustness recipe. This recipe was obtained by doing a least squares fit with a function of the form SR = aσ 2 + bσ 2 + cσ + dσ + e, where SR is the setup robustness needed, Σ is the standard deviation of the systematic setup error and σ is the standard deviation of the random setup error. The fit was done by combining the data over all of the range errors, thus the range error is not accounted for in the fit. To make an easy approximation similar to the photon therapy margin recipe a linear fit of the form SR = aσ + bσ + c is also made, for random setup errors ranging from 1 to 3 mm. This range was chosen because the systematic errors for the plans range from 1 to 3.5 mm and it is expected that the random setup errors in that case are of a similar order. 6.3 Results For the unilateral patient we found that a 3% range robustness was needed for a range error of both 1% and 2%, resulting in a D 98 of 95% for 1% and 99.8% of the population respectively. For the bilateral patient, a 3% range robustness was needed for a 1% range error, whereas a 4% robustness was needed for a 2% range error, resulting in a D 98 of 95% for 99.5% and 98.6% of the population respectively. Plots showing the maximum combinations of setup errors for a %, 1% and 2% range error that can be handled by different robustness settings are shown in figure 6.3 for the unilateral and bilateral patient. Using this figure we can for example see that for a unilateral patient a setup robustness of 4 mm is needed, in case of a 1.5 mm random setup error and 1.4 mm systematic setup error and a % range error. These plots show a difference between the unilateral and bilateral patient. In the case of the bilateral patient, a certain setup robustness can handle larger systematic setup errors than in the case of the unilateral patient. When looking at a 1.5 mm random setup error for example, we see that a unilateral patient with a 4 mm setup robustness can handle a 1.4 mm systematic setup error, whereas in the bilateral patient a 2.3 mm systematic setup error is possible for the same robustness setting. Furthermore, comparing the plots for different range errors, we see that changing the range error (while changing the range robustness accordingly) has a limited impact. The maximum systematic error remains roughly the same for different range errors. For the evaluation of the data a linear interpolation for the unilateral patient gave a 4.1 mm and 4.3 mm setup robustness which was needed for a 1.5 mm systematic and random setup error for a % and 2% range error respectively, with a range robustness of 3% for the 2% range error. For the bilateral patients we used a setup robustness of 3.3 mm and 3.4 mm for a % and 2% range error respectively, where a 4% range robustness was used for the 2% range error. The result of the evaluations done using these settings can be seen in table 6.2. In this table the percentage of the population receiving a D 98 of 95% is displayed. Only in two cases was the percentage of the population below 98%, namely for the patients used to obtain the data, but even there the worst result is 97.8% of the population. For all of the other patient at least 99% of the population had a D 98 of 95%, which means that our results are an under estimation of the actual errors that be handled by the different robustness settings for most of the patients. The robustness recipe is obtained by making a second order fit of all the points in Figure 6.3 for each patient. For the unilateral patient the resulting robustness recipe was SR =.15Σ σ Σ.6σ , the approximating linear fit is SR = 1.5Σ + 1.σ +.5. For the bilateral patient the recipe is SR =.7Σ σ Σ.7σ and the linear fit in the 1 to 3 mm range of random setup errors is SR = 1.1Σ +.7σ +.7. In figure 6.3 the recipe is displayed as a dashed line and the linear approximation is plotted as a dashed-dotted line.
68 56 Chapter 6. Article: Robustness recipes Robust recipe for patient HN1 Range error: % 2mm % 3mm % 4mm % 5mm % Robust recipe for patient HN2 Range error: % 2mm % 3mm % 4mm % 5mm % Σ (mm) 2 Σ (mm) σ (mm) σ (mm) (a) Unilateral, % range error Robust recipe for patient HN1 Range error: 1% 2mm 3% 3mm 3% 4mm 3% 5mm 3% (b) Bilateral, % range error Robust recipe for patient HN2 Range error: 1% 2mm 3% 3mm 3% 4mm 3% 5mm 3% Σ (mm) 2 Σ (mm) σ (mm) σ (mm) (c) Unilateral, 1% range error Robust recipe for patient HN1 Range error: 2% 2mm 3% 3mm 3% 4mm 3% 5mm 3% (d) Bilateral, 1% range error Robust recipe for patient HN2 Range error: 2% 2mm 4% 3mm 4% 4mm 4% 5mm 4% Σ (mm) 2 Σ (mm) σ (mm) σ (mm) (e) Unilateral, 2% range error (f) Bilateral, 2% range error Figure 6.3: Overview of combinations of random (σ) and systematic (Σ) errors that still give a D 98 of 95% of the prescribed dose for 98% of the population for range errors of %, 1% and 2%. In each plot different robustness settings are shown. The dashed lines are a quadratic fit of the data, the dashed-dot lines indicate a linear fit in the range of 1 to 3 mm of the random setup error.
69 6.4. Discussion 57 Patient Treatment group Fraction of population with D 98 = 95% (%) % range error 2% range error 1 unilateral bilateral bilateral unilateral unilateral bilateral bilateral unilateral bilateral bilateral unilateral unilateral Table 6.2: Evaluation of different patients for a 1.5 mm systematic and random setup error and a range error of % and 2%. The robustness settings were derived from the data obtained for patient 1 and Discussion In this study we have determined the robustness settings needed to get an adequate CTV coverage for a unilateral and bilateral patient. The obtained settings were validated by making treatment plans for a total of 12 patients, where there were only two cases for which the coverage was not acceptable. A difference in robustness for unilateral and bilateral patients was found, where a treatment plan for a bilateral patient was more robust than for a unilateral patient. Lastly it was seen that the setup and range robustness could be determined independently, after which the combination of the two would still give roughly the same CTV coverage as they did separately. The fact that the setup and range robustness seemed independent might be explained by the way in which the required range robustness was calculated. It was increased in steps of 1% and as a result the fraction of the population with a D 98 of 95% was almost 1% for a 1% and 2% range error in the case of the unilateral patient, higher than the 98% that we actually looked for. Therefore when combining the setup and range robustness it might be that when determining the maximum systematic error which gives an acceptable coverage, this systematic error is not much lower when a larger range error is present because the range error was over compensated for. Although it was shown that this does not pose a problem in the different patients, as they would still get an acceptable coverage for all of the evaluated plans. However maybe a smaller range robustness would also have been adequate, which would possible result in a better sparing of organs at risk. The difference between the unilateral and bilateral patients seems inherent to the patients, as the evaluation for the different patients has shown that a lower setup robustness for the bilateral patients gives approximately the same CTV coverage the unilateral patients which were evaluated for a higher robustness. Not including the original two patients the mean fraction of the population with a D 98 of 95% for a % range error was 99.5% and 99.6% for the bilateral and unilateral patients respectively. However in the case of the range robustness the bilateral patients actually needed a higher robustness setting than the unilateral patients, and even with this higher setting a lower fraction of the population received an adequate CTV coverage compared to the unilateral patients. The robustness recipes contains a constant term, which means that even if both the systematic and random error are mm, the recipe indicates that a robustness setting is needed. Not including this constant term in the fit drastically lowered the goodness of the fit. The smallest error that has been simulated when constructing the robustness recipe was.5 mm systematic setup error, with
70 58 Chapter 6. Article: Robustness recipes no random setup error, it might be that as a result the robustness recipe can not be extrapolated to very small setup errors. 6.5 Conclusion The robustness settings of multiple head and neck patients needed to achieve a adequate CTV coverage is roughly the same and can be described by a quadratic fit. It was found that bilateral patients are more robust than unilateral patients for setup errors, but less so for range errors. Furthermore setup robustness and range robustness can be set independently for these patients.
71 Chapter 7 Probabilistic treatment planning In the Chapter 6 robust treatment planning was discussed using minimax optimization. There it was shown that for head and neck patients a robustness recipe could be derived, from which the scenarios to be included in the robust optimization could be determined. This was only done for head and neck patients which means that for other patients it is still unknown what the magnitude of the errors to be included in the optimization should be to reach an adequate CTV coverage. Furthermore the scenarios determined from the recipe may not be optimal for each patient. If lower robustness settings could be used for a patient which would still give a good coverage, this would be better as this will likely spare the organs more. Therefore it would be preferable if the scenarios to be included do not have to be set explicitly, but if optimization can be done based only on the distribution of the errors, which is the basis of probabilistic treatment planning [47 5]. In this case probabilistic treatment planning will be done using PCEs. 7.1 Optimization problem The goal of treatment planning is to find the weights of the different proton pencil beams such that the resulting dose distribution matches goals and constraints that are set on the dose in the CTV and different OARs. In order to do this the dose matrix, A is used and the dose can then be determined as D i = N beamlets j=1 A i,j x j (7.1) where D i is the dose in voxel i, A i,j is the (i, j)-th element of the dose matrix, which indicates the dose received by voxel i from pencil beam j for a unit beam weight, x j is the weight of pencil beam j and N beamlets is the number of beamlets. A very simple example of an optimization problem could be min x such that N vox i=1 x X D i D i,pres (7.2) with D i,pres the prescribed dose in voxel i and X is the set of allowed pencil beam weights, which obviously can not be below and often have a maximum limit to restrict the influence of a single pencil beam. In this notation no explicit dependence on x can be seen, but this is 59
72 6 Chapter 7. Probabilistic treatment planning contained in D i which depends on the beam weights via the dose matrix, Equation (7.1). The goal of the minimization problem is to find x such that N vox i=1 D i D i,pres is minimal. The minimization can easily be done if no uncertainties come into play, because that would mean that the dose matrix is uniquely defined for a patient and the dose would only depend on the beam weights. However because the uncertainties come into play a different dose matrix is associated with each shift. Therefore the optimization problem needs to be adapted in order to take the uncertainties into account. As discussed before this is currently done by taking into account a number of pre-defined scenarios in the optimization. In the case of probabilistic optimization this is instead done by drawing a number of random samples of the different uncertainties and using the resulting scenarios in the optimization, so the only information about the uncertainties that needs to be included is their probability density function. Of course one could use these random scenarios in the minimax optimization instead of the pre-defined scenarios, however the problem is that the minimax optimization looks at each scenario individually and as a result increasing the number of scenarios will result in a very long optimization time. Thus another kind of optimization is needed which can account for multiple scenarios. This can be done in different ways, but in this case the conditional value at risk will be used Conditional value at risk The conditional value at risk (CVaR) is originally introduced as a measure of risk in the financing world [51, 52]. The CVaR is an extension of the value at risk (VaR), α β, α β (x) = min{α R : Ψ(x, α) β} (7.3) where, for a fixed x, Ψ(x, α) is the cumulative distribution function (CDF) as a function of α, Ψ(x, α) = f(x,ξ) α p ξ (ξ)dξ (7.4) where f(x, ξ) is the loss function. This means that the larger the value of f(x, ξ), the higher the loss and therefore its value should be minimized. ξ indicates the different uncertainties as before and p ξ (ξ) is the joint probability density function. In words, the VaR for a probability level β, the β-var, is the lowest possible α such that the probability of the loss function being smaller than α is at least β. As an example Figure 7.1 is shown, where the VaR is indicated, here the shaded area indicates the β. Figure 7.1: Concept of β-var and β-cvar. The shaded area indicates a probability β, thus giving the location of α β, the CVaR is in the tail of the distribution. Based on the β-var the β-cvar is defined as
73 7.1. Optimization problem 61 φ β (x) = (1 β) 1 f(x,ξ) α β (x) f(x, ξ)p ξ (ξ)dξ (7.5) which gives the conditional expectation value for the cases where f(x, ξ) α β. The β-cvar, φ β, is also depicted in Figure 7.1. The benefit of the CVaR is that it closely relates to how one would like to formulate the constraints on a treatment plan as it looks at a certain fraction of the scenarios. For example previously the dose for 98% of the population was considered as a measure for the CTV coverage, which means that in this case the 98%-CVaR can be used. This would mean that the 2% of the patients with the worst dose coverage are used in determining the CVaR. Minimizing the CVaR the optimization problem becomes min x such that φ β (x) x X (7.6) However for this optimization problem the region where f(x, ξ) α β (x) needs to be determined, which requires the calculation of the β-var. This might be time consuming and therefore it would be better if it can be avoided. Introducing F β (x, α) = α + (1 β) 1 ξ R m [f(x, ξ) α] + p ξ (ξ)dξ (7.7) where [x] + is x if x > and otherwise. The minimization problem can then be written as min x,α such that F β (x, α) x X (7.8) which will give the same result as Equation (7.6) because [52, 53] min φ β (x) = min F x β(x, α) (7.9) x,α Now the minimization also has to be done with respect to α, which has been introduced to be able to rewrite the optimization problem. F β (x, α) has a few important properties which make it a good function to use in optimization. First of all F β (x, α) is convex and continuously differentiable with respect to x and α if f(x, ξ) is convex with respect to x. The fact that it is convex is an important aspect in the optimization as this means that there is a global minimum, and the optimization algorithm will always converge to the optimal solution. Furthermore Equation (7.7) can easily be approximated by sampling the distribution p ξ (ξ) for a total of N samp samples, which gives an approximation of F β (x, α), F β (x, α) = α + N 1 samp [f(x, ξ N samp (1 β) k ) α] + (7.1) The function F β (x, α) is not continuously differentiable with respect to α anymore but it is still convex. The optimization problem can now be written as k=1 min x,α such that F β (x, α) x X (7.11) At the moment this formulation is still very general, as a loss function f(x, ξ) has not yet been defined. Choosing the loss function is where the relation to the actual problem of treatment planning is made.
74 62 Chapter 7. Probabilistic treatment planning Loss function In order to use the CVaR a loss function has to be chosen. To ensure that the optimization problem in Equation (7.11) is convex the loss function f(x, ξ) also needs to be chosen convex. Different structures have different requirements, for example in the CTV a high dose is needed while in the OARs a low dose is needed. This means that the different structures will have different lose functions. To optimize the dose in the CTV, the logarithmic tumour control probability (LTCP), which is also used in icycle [54], given as LT CP = 1 N vox e γ(dj Dpres) (7.12) N vox j=1 is used, where N vox is the number of voxels, D pres is the prescribed dose, D j is the dose in voxel j and γ is the cell sensitivity parameter. This means that for now f(x, ξ) = 1 Nvox N vox No explicit dependence on the uncertainty and beam weights is shown in the LTCP, but both are contained in the dose D j. The LTCP is a convex version of the tumour control probability (TCP), where the TCP indicates the probability that a tumour will be cured when it receives a certain dose. The optimization will only be done for a head and neck patient, for which γ =.75 is taken. The LTCP strongly punishes a dose lower than the prescribed dose, but for doses higher than the prescribed dose it will go to, it is therefore a good loss function, as a low value of the LTCP will mean a high dose in the CTV. To make sure that the dose does not get too high, a limit is set on the maximum dose in the nominal scenario. The dose in the nominal scenario is not allowed to be higher than 17% of the prescribed dose in any of the voxels. Furthermore a constraint is set on the minimum dose, namely that in the nominal scenario the dose in all voxels should be at least 95% of the prescribed dose. Of course these constraints should be expanded in the future to also take into account multiple scenarios instead of only the nominal scenario, but for now these constraints were chosen as this keeps the problem convex [55]. Furthermore the allowed values of the beam weights must be set. Obviously the beam weights have to be positive and a maximum beam weight of 3 is selected, as it was seen that the beam weights obtained using icycle are generally not larger than that. All in all therefore the optimization problems becomes j=1 e γ(dj Dpres). min x,α N samp 1 α + N samp(1 β) [f(x, ξ k ) α] + k=1 such that A nom x.95d pres A nom x 1.7D pres x i i x i 3 i (7.13) where f(x, ξ) = 1 Nvox N vox j=1 e γ(dj Dpres) and β =.98, to consider 98% of the population, have been chosen. At first only the dose in the CTV high will be considered, with a prescription dose of 66 Gy. As an OAR the parotid is included, as this was the OAR with the highest priority in the wish-list. Because the dose in the parotid needs to be minimized, the maximum dose in the parotid is used as the loss function. f(x, ξ) = 1 N vox e γ(dj Dpres) + ɛ max(d N parotid ) (7.14) vox j=1 where ɛ is a parameter that can be set as a weighting factor between the dose in the CTV and in the parotid, here ɛ =.2 has been chosen. The number of scenarios included in the optimization N samp need to be large enough to ensure that the optimization will also give a good results for the scenarios which were not included in the optimization. For each sample a different dose matrix is needed, as a different dose matrix is associated with each scenario. Using the dose engine for this will be problematic as it will be time consuming to calculate the dose matrix for a
75 7.2. PCE of dose matrix 63 lot of scenarios. Therefore a PCE of the dose matrix will be made, which can be used to calculate the dose matrix for different scenarios. 7.2 PCE of dose matrix Previously a PCE of the dose distribution has been made, but now a PCE of the dose matrix is needed, as that is used in the optimization. This will increase the number of coefficients of the PCE tremendously, because now for each voxel the different pencil beams also need to be included. Instead of N voxels outputs earlier, there are now a total of N voxels N pencilbeams outputs. To reduce the coefficients in this case two methods are used. First of all only voxels which are actually used in the optimization are included. Previously voxels were included based on a dose threshold, but then voxels were included which did not belong to any structure and thus will not be used in the optimization. Only the CTV high and the right parotid will be taken into account in this optimization, so only those voxels are included in the PCE construction. The second way of reducing the number of coefficients is by only selecting certain pencil beams which can be used in the optimization. Instead of starting from scratch to select the pencil beams as is usually done, the beams from a treatment plan generate by icycle are used. The number of pencil beams is further reduced by only keeping beams that are influencing either the CTV high or the parotid, since the rest of the beams will not have any effect in the optimization. This has been determined by considering the coefficients of the PCE. This resulted in a total of 35 beamlets being used. The PCE of the dose matrix was constructed much in the same way as the PCE for a dose distribution. But now instead of calculating the dose distribution for the different quadrature points using the dose engine, the dose matrix is calculated. In Figure 7.2 the exact response and the approximation from the PCE for two of the elements of the dose matrix can be seen, where a GO5s4 was used. It is now harder to properly quantify whether the PCE gives a good approximation of the exact dose matrix, as a gamma evaluation is difficult to do now. Not only do different scenarios need to be considered, but also different beam weights, which means that too many dose distributions need to be calculated which is not feasible. But based on earlier results, and the shown figures, it is assumed that the PCE is accurate enough. If this is not the case, the beam weights obtained in the optimization will be wrong. Then when evaluating the plans this will be visible and thus in the end it can be determined whether the PCE was actually accurate enough. Using the PCE a total of N samp = 5 scenarios were used Exact PCE Exact PCE Dose matrix element (Gy/GP) Dose matrix element (Gy/GP) x-shift (mm) x-shift (mm) Figure 7.2: Dependence of two different dose matrix elements as a function of the x-shift, for voxels located in the CTV high. An exact calculation and a GO5s4PO5 PCE are compared.
76 64 Chapter 7. Probabilistic treatment planning 7.3 Optimization algorithm The optimization algorithm that will be used is the built-in patternsearch of matlab [56]. Patternsearch is a derivative free optimization algorithm, which minimizes the problem by evaluating the effect of changing the different beam weights with a certain step size. This method was chosen because it was a fast algorithm compared to the other built-in optimizer which did use derivatives. An overview of the way patternsearch works is given in 7.3. The patternsearch starts off with a certain mesh size defined by the user, this determines the step size taken in each direction. It then evaluates the points in the mesh one by one and if a point results in a lower function value, the beam weights are updated and the mesh size is increased by a certain factor, the expansion coefficient defined by the user. This new mesh size is then used to construct new points to evaluate and once again the optimizer will go over the different points in the same order. If all of the points are unsuccessful the mesh size is reduced to once again create a new mesh, this is done using the contraction coefficient as defined by the user. This process is repeated untill the maximum number of iterations has been reached. In the optimization an initial mesh size of 8 has been used, with an expansion coefficient of 1.2 and a contraction coefficient of.2 A maximum allowed mesh size of 15 was used. Because the algorithm goes over the values in a certain order it is beneficial to place the most important beams first, as the algorithm will then evaluate these beams first. Important beams are beams that affect a lot of voxels. In this way in the first few iterations the optimization will already be very effective because the dose distribution is already influenced heavily by the first few beams. The fine tuning of the dose can then be done with the last few beam weights. 7.4 Results of optimization The optimization was done at first by only including the high-dose CTV, for 1, 25 and 5 iterations of the optimization algorithm. After the beam weights were obtained, a dose PCE was constructed for the plan and for each case a DPH was made, which can be seen in Figure 7.4, where it is also compared to the initial values of the beam weights and the plan from which the beams were chosen. As can be seen the optimization very quickly improves from the initial weight and after only 1 iterations the dose coverage is already pretty high. Increasing the number of iterations even more does not seem to have a very large effect, although it does come closer to the original plan. The coverage of the original plan is not achieved, but it comes very close. The time needed for different numbers of iterations can be seen in Table 7.1. As expected the first few iterations are rather fast and already have a big influence on the dose distribution. Based on these results the plan obtained after 25 iterations is used. The dose distribution of this plan in the nominal scenario is shown in Figure 7.5. Here the dose distribution is shown twice with two different scales, because the dose outside of the CTV is so large that otherwise it would not be possible to see the dose distribution in the CTV itself. The resulting dose outside of the CTV is really high, up to 39 Gy, which means that the patient would be dead if this dose was actually given. This is a result of the fact that only the CTV high was considered in the optimization. Looking at the other scale, where a dose above 75 Gy is also displayed as 75 Gy, it can be seen that the dose distribution in the CTV itself seems acceptable. Iterations Calculation time 1 24 minutes minutes minutes Table 7.1: Calculation times for different numbers of iterations.
77 7.4. Results of optimization 65 Create initial mesh Activate first vector Evaluate current active vector Set next vector active No Increase mesh size No Function value less than previous? No Evaluated all directions? Yes Decrease grid size, determine new mesh, new iteration Maximum number of iterations reached? Yes Update beam weights, next iteration Yes Optimization finished Figure 7.3: Overview of the patternsearch optimization algorithm. 1 9 Population (%) Initial plan 1 iterations 25 iterations 5 iterations Original plan D 98 (%) Figure 7.4: Comparison of different numbers of iterations used in the optimization. The initial plan shows the plan for the beam weights used as the starting point of the optimization.
78 66 Chapter 7. Probabilistic treatment planning Figure 7.5: Dose distribution in the nominal case of treatment plan obtained using the CVaR, after 25 iterations. Color bar indicated dose in Gy, where two different scales are used on the left and right figure Population (%) Initial 1 iter 25 iter Plan with parotid Original plan D 98 (Gy) Figure 7.6: DPH of CTV high for different plans. The plan where the parotid has been included gives a very similar result as the plan in which it was not included. To reduce the unacceptable high dose, the right parotid will be taken into account as an OAR, where the beam weights obtained from the previous optimization, after 25 iterations, are used as the initial beam weights for this optimization. The optimization was run for an additional 25 iterations, which took an additional 6 and a half hours, resulting in a total planning time of around 8 hours. Once again a DPH of the CTV high was made, which can be seen in Figure 7.6, where it was compared with the previously obtained result. As can be seen the plan including the parotid is very similar to the previously obtained plan without it. This is good, as this means that the dose in the parotid can be minimized, without sacrificing the high dose in the CTV. To look at the dose in the parotid a DPH of the D 2 in the parotid is made, shown in Figure 7.7, here it can be seen that the dose in the parotid is actually lower than it was in the original plan, from which the beamlets that are used are determined. This might have to do with the fact that in this case the parotid was the only OAR taken into account, and it might become harder to keep the dose in the parotid low while also making sure that other OARs do not receive a high dose. But because the dose in the parotid is lower than it was in the actual treatment plan, this means that this is an acceptable dose for the parotid. The new dose distribution can be seen in Figure 7.8 where it can be seen that the dose distribution for the nominal scenario is a lot better than it was previously. The dose is still really high at points, but now the maximum dose is 1 Gy instead of 39 Gy. A better sparing of the right parotid compared to Figure 7.5 can also be seen. Of course it is also important to look at the dose distribution for a case where an error occurs, as the goal was to get a good dose distribution even in the case of errors. Therefore for a 2 mm
Robustness Recipes for Proton Therapy
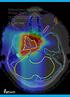 Robustness Recipes for Proton Therapy Polynomial Chaos Expansion as a tool to construct robustness recipes for proton therapy C.E. ter Haar Delft University of Technology Robustness Recipes for Proton
Robustness Recipes for Proton Therapy Polynomial Chaos Expansion as a tool to construct robustness recipes for proton therapy C.E. ter Haar Delft University of Technology Robustness Recipes for Proton
ROBUST OPTIMIZATION THE END OF PTV AND THE BEGINNING OF SMART DOSE CLOUD. Moe Siddiqui, April 08, 2017
 ROBUST OPTIMIZATION THE END OF PTV AND THE BEGINNING OF SMART DOSE CLOUD Moe Siddiqui, April 08, 2017 Agenda Background IRCU 50 - Disclaimer - Uncertainties Robust optimization Use Cases Lung Robust 4D
ROBUST OPTIMIZATION THE END OF PTV AND THE BEGINNING OF SMART DOSE CLOUD Moe Siddiqui, April 08, 2017 Agenda Background IRCU 50 - Disclaimer - Uncertainties Robust optimization Use Cases Lung Robust 4D
Radiation therapy treatment plan optimization
 H. Department of Industrial and Operations Engineering The University of Michigan, Ann Arbor, Michigan MOPTA Lehigh University August 18 20, 2010 Outline 1 Introduction Radiation therapy delivery 2 Treatment
H. Department of Industrial and Operations Engineering The University of Michigan, Ann Arbor, Michigan MOPTA Lehigh University August 18 20, 2010 Outline 1 Introduction Radiation therapy delivery 2 Treatment
C.M.H. Hartman. Master Thesis
 SENSITIVITY AND UNCERTAINTY ANALYSIS IN PROTON THERAPY TREATMENT PLANS USING POLYNOMIAL CHAOS METHODS C.M.H. Hartman Master Thesis Supervisors: Dr. ir. D. Lathouwers Dr. M. Hoogeman Z. Perkó, MSc S. van
SENSITIVITY AND UNCERTAINTY ANALYSIS IN PROTON THERAPY TREATMENT PLANS USING POLYNOMIAL CHAOS METHODS C.M.H. Hartman Master Thesis Supervisors: Dr. ir. D. Lathouwers Dr. M. Hoogeman Z. Perkó, MSc S. van
Coverage based treatment planning to accommodate organ deformable motions and contouring uncertainties for prostate treatment. Huijun Xu, Ph.D.
 Coverage based treatment planning to accommodate organ deformable motions and contouring uncertainties for prostate treatment Huijun Xu, Ph.D. Acknowledgement and Disclosure Dr. Jeffrey Siebers Dr. DJ
Coverage based treatment planning to accommodate organ deformable motions and contouring uncertainties for prostate treatment Huijun Xu, Ph.D. Acknowledgement and Disclosure Dr. Jeffrey Siebers Dr. DJ
IMRT site-specific procedure: Prostate (CHHiP)
 IMRT site-specific procedure: Prostate (CHHiP) Scope: To provide site specific instructions for the planning of CHHIP IMRT patients Responsibilities: Radiotherapy Physicists, HPC Registered Therapy Radiographers
IMRT site-specific procedure: Prostate (CHHiP) Scope: To provide site specific instructions for the planning of CHHIP IMRT patients Responsibilities: Radiotherapy Physicists, HPC Registered Therapy Radiographers
Interactive Treatment Planning in Cancer Radiotherapy
 Interactive Treatment Planning in Cancer Radiotherapy Mohammad Shakourifar Giulio Trigila Pooyan Shirvani Ghomi Abraham Abebe Sarah Couzens Laura Noreña Wenling Shang June 29, 212 1 Introduction Intensity
Interactive Treatment Planning in Cancer Radiotherapy Mohammad Shakourifar Giulio Trigila Pooyan Shirvani Ghomi Abraham Abebe Sarah Couzens Laura Noreña Wenling Shang June 29, 212 1 Introduction Intensity
REAL-TIME ADAPTIVITY IN HEAD-AND-NECK AND LUNG CANCER RADIOTHERAPY IN A GPU ENVIRONMENT
 REAL-TIME ADAPTIVITY IN HEAD-AND-NECK AND LUNG CANCER RADIOTHERAPY IN A GPU ENVIRONMENT Anand P Santhanam Assistant Professor, Department of Radiation Oncology OUTLINE Adaptive radiotherapy for head and
REAL-TIME ADAPTIVITY IN HEAD-AND-NECK AND LUNG CANCER RADIOTHERAPY IN A GPU ENVIRONMENT Anand P Santhanam Assistant Professor, Department of Radiation Oncology OUTLINE Adaptive radiotherapy for head and
GPU applications in Cancer Radiation Therapy at UCSD. Steve Jiang, UCSD Radiation Oncology Amit Majumdar, SDSC Dongju (DJ) Choi, SDSC
 GPU applications in Cancer Radiation Therapy at UCSD Steve Jiang, UCSD Radiation Oncology Amit Majumdar, SDSC Dongju (DJ) Choi, SDSC Conventional Radiotherapy SIMULATION: Construciton, Dij Days PLANNING:
GPU applications in Cancer Radiation Therapy at UCSD Steve Jiang, UCSD Radiation Oncology Amit Majumdar, SDSC Dongju (DJ) Choi, SDSC Conventional Radiotherapy SIMULATION: Construciton, Dij Days PLANNING:
Chapter 9 Field Shaping: Scanning Beam
 Chapter 9 Field Shaping: Scanning Beam X. Ronald Zhu, Ph.D. Department of Radiation Physics M. D. Anderson Cancer Center Houston, TX June 14-18, 2015 AAPM - Summer School 2015, Colorado Spring Acknowledgement
Chapter 9 Field Shaping: Scanning Beam X. Ronald Zhu, Ph.D. Department of Radiation Physics M. D. Anderson Cancer Center Houston, TX June 14-18, 2015 AAPM - Summer School 2015, Colorado Spring Acknowledgement
Performance of a hybrid Monte Carlo-Pencil Beam dose algorithm for proton therapy inverse planning
 Performance of a hybrid Monte Carlo-Pencil Beam dose algorithm for proton therapy inverse planning Ana Marıa Barragan Montero, a) and Kevin Souris Universite catholique de Louvain, Institut de Recherche
Performance of a hybrid Monte Carlo-Pencil Beam dose algorithm for proton therapy inverse planning Ana Marıa Barragan Montero, a) and Kevin Souris Universite catholique de Louvain, Institut de Recherche
7/29/2017. Making Better IMRT Plans Using a New Direct Aperture Optimization Approach. Aim of Radiotherapy Research. Aim of Radiotherapy Research
 Making Better IMRT Plans Using a New Direct Aperture Optimization Approach Dan Nguyen, Ph.D. Division of Medical Physics and Engineering Department of Radiation Oncology UT Southwestern AAPM Annual Meeting
Making Better IMRT Plans Using a New Direct Aperture Optimization Approach Dan Nguyen, Ph.D. Division of Medical Physics and Engineering Department of Radiation Oncology UT Southwestern AAPM Annual Meeting
Monaco Concepts and IMRT / VMAT Planning LTAMON0003 / 3.0
 and IMRT / VMAT Planning LTAMON0003 / 3.0 and Planning Objectives By the end of this presentation you can: Describe the cost functions in Monaco and recognize their application in building a successful
and IMRT / VMAT Planning LTAMON0003 / 3.0 and Planning Objectives By the end of this presentation you can: Describe the cost functions in Monaco and recognize their application in building a successful
A Generation Methodology for Numerical Phantoms with Statistically Relevant Variability of Geometric and Physical Properties
 A Generation Methodology for Numerical Phantoms with Statistically Relevant Variability of Geometric and Physical Properties Steven Dolly 1, Eric Ehler 1, Yang Lou 2, Mark Anastasio 2, Hua Li 2 (1) University
A Generation Methodology for Numerical Phantoms with Statistically Relevant Variability of Geometric and Physical Properties Steven Dolly 1, Eric Ehler 1, Yang Lou 2, Mark Anastasio 2, Hua Li 2 (1) University
Current state of multi-criteria treatment planning
 Current state of multi-criteria treatment planning June 11, 2010 Fall River NE AAPM meeting David Craft Massachusetts General Hospital Talk outline - Overview of optimization - Multi-criteria optimization
Current state of multi-criteria treatment planning June 11, 2010 Fall River NE AAPM meeting David Craft Massachusetts General Hospital Talk outline - Overview of optimization - Multi-criteria optimization
A Fully-Automated Intensity-Modulated Radiation Therapy Planning System
 A Fully-Automated Intensity-Modulated Radiation Therapy Planning System Shabbir Ahmed, Ozan Gozbasi, Martin Savelsbergh Georgia Institute of Technology Ian Crocker, Tim Fox, Eduard Schreibmann Emory University
A Fully-Automated Intensity-Modulated Radiation Therapy Planning System Shabbir Ahmed, Ozan Gozbasi, Martin Savelsbergh Georgia Institute of Technology Ian Crocker, Tim Fox, Eduard Schreibmann Emory University
A hybrid framework for optimizing beam angles in radiation therapy planning
 A hybrid framework for optimizing beam angles in radiation therapy planning Gino J. Lim and Laleh Kardar and Wenhua Cao December 29, 2013 Abstract The purpose of this paper is twofold: (1) to examine strengths
A hybrid framework for optimizing beam angles in radiation therapy planning Gino J. Lim and Laleh Kardar and Wenhua Cao December 29, 2013 Abstract The purpose of this paper is twofold: (1) to examine strengths
Basic Radiation Oncology Physics
 Basic Radiation Oncology Physics T. Ganesh, Ph.D., DABR Chief Medical Physicist Fortis Memorial Research Institute Gurgaon Acknowledgment: I gratefully acknowledge the IAEA resources of teaching slides
Basic Radiation Oncology Physics T. Ganesh, Ph.D., DABR Chief Medical Physicist Fortis Memorial Research Institute Gurgaon Acknowledgment: I gratefully acknowledge the IAEA resources of teaching slides
RADIOMICS: potential role in the clinics and challenges
 27 giugno 2018 Dipartimento di Fisica Università degli Studi di Milano RADIOMICS: potential role in the clinics and challenges Dr. Francesca Botta Medical Physicist Istituto Europeo di Oncologia (Milano)
27 giugno 2018 Dipartimento di Fisica Università degli Studi di Milano RADIOMICS: potential role in the clinics and challenges Dr. Francesca Botta Medical Physicist Istituto Europeo di Oncologia (Milano)
How would, or how does, the patient position (chin extended) affect your beam arrangement?
 1 Megan Sullivan Clinical Practicum II Parotid Lab July 29, 2016 PLAN 1: IPSILATERAL WEDGE PAIR TECHNIQUE The ipsilateral wedge pair technique consisted of an anterior oblique field at 45 degrees and a
1 Megan Sullivan Clinical Practicum II Parotid Lab July 29, 2016 PLAN 1: IPSILATERAL WEDGE PAIR TECHNIQUE The ipsilateral wedge pair technique consisted of an anterior oblique field at 45 degrees and a
ELECTRON DOSE KERNELS TO ACCOUNT FOR SECONDARY PARTICLE TRANSPORT IN DETERMINISTIC SIMULATIONS
 Computational Medical Physics Working Group Workshop II, Sep 30 Oct 3, 2007 University of Florida (UF), Gainesville, Florida USA on CD-ROM, American Nuclear Society, LaGrange Park, IL (2007) ELECTRON DOSE
Computational Medical Physics Working Group Workshop II, Sep 30 Oct 3, 2007 University of Florida (UF), Gainesville, Florida USA on CD-ROM, American Nuclear Society, LaGrange Park, IL (2007) ELECTRON DOSE
Monte Carlo methods in proton beam radiation therapy. Harald Paganetti
 Monte Carlo methods in proton beam radiation therapy Harald Paganetti Introduction: Proton Physics Electromagnetic energy loss of protons Distal distribution Dose [%] 120 100 80 60 40 p e p Ionization
Monte Carlo methods in proton beam radiation therapy Harald Paganetti Introduction: Proton Physics Electromagnetic energy loss of protons Distal distribution Dose [%] 120 100 80 60 40 p e p Ionization
Monaco VMAT. The Next Generation in IMRT/VMAT Planning. Paulo Mathias Customer Support TPS Application
 Monaco VMAT The Next Generation in IMRT/VMAT Planning Paulo Mathias Customer Support TPS Application 11.05.2011 Background What is Monaco? Advanced IMRT/VMAT treatment planning system from Elekta Software
Monaco VMAT The Next Generation in IMRT/VMAT Planning Paulo Mathias Customer Support TPS Application 11.05.2011 Background What is Monaco? Advanced IMRT/VMAT treatment planning system from Elekta Software
A Fully-Automated Intensity-Modulated Radiation Therapy Planning System
 A Fully-Automated Intensity-Modulated Radiation Therapy Planning System Shabbir Ahmed, Ozan Gozbasi, Martin Savelsbergh Georgia Institute of Technology Tim Fox, Ian Crocker, Eduard Schreibmann Emory University
A Fully-Automated Intensity-Modulated Radiation Therapy Planning System Shabbir Ahmed, Ozan Gozbasi, Martin Savelsbergh Georgia Institute of Technology Tim Fox, Ian Crocker, Eduard Schreibmann Emory University
Auto-Segmentation Using Deformable Image Registration. Disclosure. Objectives 8/4/2011
 Auto-Segmentation Using Deformable Image Registration Lei Dong, Ph.D. Dept. of Radiation Physics University of Texas MD Anderson Cancer Center, Houston, Texas AAPM Therapy Educational Course Aug. 4th 2011
Auto-Segmentation Using Deformable Image Registration Lei Dong, Ph.D. Dept. of Radiation Physics University of Texas MD Anderson Cancer Center, Houston, Texas AAPM Therapy Educational Course Aug. 4th 2011
NEW METHOD OF COLLECTING OUTPUT FACTORS FOR COMMISSIONING LINEAR ACCELERATORS WITH SPECIAL EMPHASIS
 NEW METHOD OF COLLECTING OUTPUT FACTORS FOR COMMISSIONING LINEAR ACCELERATORS WITH SPECIAL EMPHASIS ON SMALL FIELDS AND INTENSITY MODULATED RADIATION THERAPY by Cindy D. Smith A Thesis Submitted to the
NEW METHOD OF COLLECTING OUTPUT FACTORS FOR COMMISSIONING LINEAR ACCELERATORS WITH SPECIAL EMPHASIS ON SMALL FIELDS AND INTENSITY MODULATED RADIATION THERAPY by Cindy D. Smith A Thesis Submitted to the
CONTOURING ACCURACY. What Have We Learned? And Where Do We Go From Here? BEN NELMS, PH.D. AUGUST 15, 2016
 CONTOURING ACCURACY What Have We Learned? And Where Do We Go From Here? BEN NELMS, PH.D. AUGUST 15, 2016 FIRST THINGS FIRST Happy Medical Dosimetrist s Week! OUTLINE 1. Objectives 2. The importance of
CONTOURING ACCURACY What Have We Learned? And Where Do We Go From Here? BEN NELMS, PH.D. AUGUST 15, 2016 FIRST THINGS FIRST Happy Medical Dosimetrist s Week! OUTLINE 1. Objectives 2. The importance of
Dose Calculation and Optimization Algorithms: A Clinical Perspective
 Dose Calculation and Optimization Algorithms: A Clinical Perspective Daryl P. Nazareth, PhD Roswell Park Cancer Institute, Buffalo, NY T. Rock Mackie, PhD University of Wisconsin-Madison David Shepard,
Dose Calculation and Optimization Algorithms: A Clinical Perspective Daryl P. Nazareth, PhD Roswell Park Cancer Institute, Buffalo, NY T. Rock Mackie, PhD University of Wisconsin-Madison David Shepard,
Creating a Knowledge Based Model using RapidPlan TM : The Henry Ford Experience
 DVH Estimates Creating a Knowledge Based Model using RapidPlan TM : The Henry Ford Experience Karen Chin Snyder, MS, DABR AAMD Region V Meeting October 4, 2014 Disclosures The Department of Radiation Oncology
DVH Estimates Creating a Knowledge Based Model using RapidPlan TM : The Henry Ford Experience Karen Chin Snyder, MS, DABR AAMD Region V Meeting October 4, 2014 Disclosures The Department of Radiation Oncology
8/3/2017. Contour Assessment for Quality Assurance and Data Mining. Objective. Outline. Tom Purdie, PhD, MCCPM
 Contour Assessment for Quality Assurance and Data Mining Tom Purdie, PhD, MCCPM Objective Understand the state-of-the-art in contour assessment for quality assurance including data mining-based techniques
Contour Assessment for Quality Assurance and Data Mining Tom Purdie, PhD, MCCPM Objective Understand the state-of-the-art in contour assessment for quality assurance including data mining-based techniques
Electron Dose Kernels (EDK) for Secondary Particle Transport in Deterministic Simulations
 Electron Dose Kernels (EDK) for Secondary Particle Transport in Deterministic Simulations A. Al-Basheer, G. Sjoden, M. Ghita Computational Medical Physics Team Nuclear & Radiological Engineering University
Electron Dose Kernels (EDK) for Secondary Particle Transport in Deterministic Simulations A. Al-Basheer, G. Sjoden, M. Ghita Computational Medical Physics Team Nuclear & Radiological Engineering University
Investigation of tilted dose kernels for portal dose prediction in a-si electronic portal imagers
 Investigation of tilted dose kernels for portal dose prediction in a-si electronic portal imagers Krista Chytyk MSc student Supervisor: Dr. Boyd McCurdy Introduction The objective of cancer radiotherapy
Investigation of tilted dose kernels for portal dose prediction in a-si electronic portal imagers Krista Chytyk MSc student Supervisor: Dr. Boyd McCurdy Introduction The objective of cancer radiotherapy
A derivative-free multistart framework for an automated noncoplanar beam angle optimization in IMRT
 A derivative-free multistart framework for an automated noncoplanar beam angle optimization in IMRT Humberto Rocha and Joana Dias FEUC and Inesc-Coimbra, University of Coimbra, Portugal 5 1 Tiago Ventura
A derivative-free multistart framework for an automated noncoplanar beam angle optimization in IMRT Humberto Rocha and Joana Dias FEUC and Inesc-Coimbra, University of Coimbra, Portugal 5 1 Tiago Ventura
High Throughput Computing and Sampling Issues for Optimization in Radiotherapy
 High Throughput Computing and Sampling Issues for Optimization in Radiotherapy Michael C. Ferris, University of Wisconsin Alexander Meeraus, GAMS Development Corporation Optimization Days, Montreal, May
High Throughput Computing and Sampling Issues for Optimization in Radiotherapy Michael C. Ferris, University of Wisconsin Alexander Meeraus, GAMS Development Corporation Optimization Days, Montreal, May
Significance of time-dependent geometries for Monte Carlo simulations in radiation therapy. Harald Paganetti
 Significance of time-dependent geometries for Monte Carlo simulations in radiation therapy Harald Paganetti Modeling time dependent geometrical setups Key to 4D Monte Carlo: Geometry changes during the
Significance of time-dependent geometries for Monte Carlo simulations in radiation therapy Harald Paganetti Modeling time dependent geometrical setups Key to 4D Monte Carlo: Geometry changes during the
OPTIMIZATION MODELS FOR RADIATION THERAPY: TREATMENT PLANNING AND PATIENT SCHEDULING
 OPTIMIZATION MODELS FOR RADIATION THERAPY: TREATMENT PLANNING AND PATIENT SCHEDULING By CHUNHUA MEN A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF
OPTIMIZATION MODELS FOR RADIATION THERAPY: TREATMENT PLANNING AND PATIENT SCHEDULING By CHUNHUA MEN A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF
VALIDATION OF DIR. Raj Varadhan, PhD, DABMP Minneapolis Radiation Oncology
 VALIDATION OF DIR Raj Varadhan, PhD, DABMP Minneapolis Radiation Oncology Overview Basics: Registration Framework, Theory Discuss Validation techniques Using Synthetic CT data & Phantoms What metrics to
VALIDATION OF DIR Raj Varadhan, PhD, DABMP Minneapolis Radiation Oncology Overview Basics: Registration Framework, Theory Discuss Validation techniques Using Synthetic CT data & Phantoms What metrics to
UNIVERSITY OF SOUTHAMPTON
 UNIVERSITY OF SOUTHAMPTON PHYS2007W1 SEMESTER 2 EXAMINATION 2014-2015 MEDICAL PHYSICS Duration: 120 MINS (2 hours) This paper contains 10 questions. Answer all questions in Section A and only two questions
UNIVERSITY OF SOUTHAMPTON PHYS2007W1 SEMESTER 2 EXAMINATION 2014-2015 MEDICAL PHYSICS Duration: 120 MINS (2 hours) This paper contains 10 questions. Answer all questions in Section A and only two questions
An experimental investigation on the effect of beam angle optimization on the reduction of beam numbers in IMRT of head and neck tumors
 JOURNAL OF APPLIED CLINICAL MEDICAL PHYSICS, VOLUME 13, NUMBER 4, 2012 An experimental investigation on the effect of beam angle optimization on the reduction of beam numbers in IMRT of head and neck tumors
JOURNAL OF APPLIED CLINICAL MEDICAL PHYSICS, VOLUME 13, NUMBER 4, 2012 An experimental investigation on the effect of beam angle optimization on the reduction of beam numbers in IMRT of head and neck tumors
arxiv: v1 [physics.med-ph] 22 Dec 2011
![arxiv: v1 [physics.med-ph] 22 Dec 2011 arxiv: v1 [physics.med-ph] 22 Dec 2011](/thumbs/86/93194414.jpg) Including Robustness in Multi-criteria Optimization for Intensity Modulated Proton Therapy arxiv:2.5362v [physics.med-ph] 22 Dec 20 Wei Chen, Jan Unkelbach, Alexei Trofimov, Thomas Madden, Hanne Kooy,
Including Robustness in Multi-criteria Optimization for Intensity Modulated Proton Therapy arxiv:2.5362v [physics.med-ph] 22 Dec 20 Wei Chen, Jan Unkelbach, Alexei Trofimov, Thomas Madden, Hanne Kooy,
A fluence convolution method to account for respiratory motion in three-dimensional dose calculations of the liver: A Monte Carlo study
 A fluence convolution method to account for respiratory motion in three-dimensional dose calculations of the liver: A Monte Carlo study Indrin J. Chetty, a) Mihaela Rosu, Neelam Tyagi, Lon H. Marsh, Daniel
A fluence convolution method to account for respiratory motion in three-dimensional dose calculations of the liver: A Monte Carlo study Indrin J. Chetty, a) Mihaela Rosu, Neelam Tyagi, Lon H. Marsh, Daniel
Photon Dose Algorithms and Physics Data Modeling in modern RTP
 Photon Dose Algorithms and Physics Data Modeling in modern RTP Niko Papanikolaou, PhD Professor and Director of Medical Physics University of Texas Health Science Center of San Antonio Cancer Therapy &
Photon Dose Algorithms and Physics Data Modeling in modern RTP Niko Papanikolaou, PhD Professor and Director of Medical Physics University of Texas Health Science Center of San Antonio Cancer Therapy &
CHAPTER 9 INFLUENCE OF SMOOTHING ALGORITHMS IN MONTE CARLO DOSE CALCULATIONS OF CYBERKNIFE TREATMENT PLANS: A LUNG PHANTOM STUDY
 148 CHAPTER 9 INFLUENCE OF SMOOTHING ALGORITHMS IN MONTE CARLO DOSE CALCULATIONS OF CYBERKNIFE TREATMENT PLANS: A LUNG PHANTOM STUDY 9.1 INTRODUCTION 9.1.1 Dose Calculation Algorithms Dose calculation
148 CHAPTER 9 INFLUENCE OF SMOOTHING ALGORITHMS IN MONTE CARLO DOSE CALCULATIONS OF CYBERKNIFE TREATMENT PLANS: A LUNG PHANTOM STUDY 9.1 INTRODUCTION 9.1.1 Dose Calculation Algorithms Dose calculation
Proton dose calculation algorithms and configuration data
 Proton dose calculation algorithms and configuration data Barbara Schaffner PTCOG 46 Educational workshop in Wanjie, 20. May 2007 VARIAN Medical Systems Agenda Broad beam algorithms Concept of pencil beam
Proton dose calculation algorithms and configuration data Barbara Schaffner PTCOG 46 Educational workshop in Wanjie, 20. May 2007 VARIAN Medical Systems Agenda Broad beam algorithms Concept of pencil beam
CHAPTER 2. Morphometry on rodent brains. A.E.H. Scheenstra J. Dijkstra L. van der Weerd
 CHAPTER 2 Morphometry on rodent brains A.E.H. Scheenstra J. Dijkstra L. van der Weerd This chapter was adapted from: Volumetry and other quantitative measurements to assess the rodent brain, In vivo NMR
CHAPTER 2 Morphometry on rodent brains A.E.H. Scheenstra J. Dijkstra L. van der Weerd This chapter was adapted from: Volumetry and other quantitative measurements to assess the rodent brain, In vivo NMR
Dynamic digital phantoms
 Dynamic digital phantoms In radiation research the term phantom is used to describe an inanimate object or system used to tune the performance of radiation imaging or radiotherapeutic devices. A wide range
Dynamic digital phantoms In radiation research the term phantom is used to describe an inanimate object or system used to tune the performance of radiation imaging or radiotherapeutic devices. A wide range
ICARO Vienna April Implementing 3D conformal radiotherapy and IMRT in clinical practice: Recommendations of IAEA- TECDOC-1588
 ICARO Vienna April 27-29 2009 Implementing 3D conformal radiotherapy and IMRT in clinical practice: Recommendations of IAEA- TECDOC-1588 M. Saiful Huq, Ph.D., Professor and Director, Dept. of Radiation
ICARO Vienna April 27-29 2009 Implementing 3D conformal radiotherapy and IMRT in clinical practice: Recommendations of IAEA- TECDOC-1588 M. Saiful Huq, Ph.D., Professor and Director, Dept. of Radiation
Comparison of internal and external dose conversion factors using ICRP adult male and MEET Man voxel model phantoms.
 Comparison of internal and external dose conversion factors using ICRP adult male and MEET Man voxel model phantoms. D.Leone, A.Häußler Intitute for Nuclear Waste Disposal, Karlsruhe Institute for Technology,
Comparison of internal and external dose conversion factors using ICRP adult male and MEET Man voxel model phantoms. D.Leone, A.Häußler Intitute for Nuclear Waste Disposal, Karlsruhe Institute for Technology,
Brilliance CT Big Bore.
 1 2 2 There are two methods of RCCT acquisition in widespread clinical use: cine axial and helical. In RCCT with cine axial acquisition, repeat CT images are taken each couch position while recording respiration.
1 2 2 There are two methods of RCCT acquisition in widespread clinical use: cine axial and helical. In RCCT with cine axial acquisition, repeat CT images are taken each couch position while recording respiration.
Use of Deformable Image Registration in Radiation Therapy. Colin Sims, M.Sc. Accuray Incorporated 1
 Use of Deformable Image Registration in Radiation Therapy Colin Sims, M.Sc. Accuray Incorporated 1 Overview of Deformable Image Registration (DIR) Algorithms that can deform one dataset to another have
Use of Deformable Image Registration in Radiation Therapy Colin Sims, M.Sc. Accuray Incorporated 1 Overview of Deformable Image Registration (DIR) Algorithms that can deform one dataset to another have
Segmentation Using a Region Growing Thresholding
 Segmentation Using a Region Growing Thresholding Matei MANCAS 1, Bernard GOSSELIN 1, Benoît MACQ 2 1 Faculté Polytechnique de Mons, Circuit Theory and Signal Processing Laboratory Bâtiment MULTITEL/TCTS
Segmentation Using a Region Growing Thresholding Matei MANCAS 1, Bernard GOSSELIN 1, Benoît MACQ 2 1 Faculté Polytechnique de Mons, Circuit Theory and Signal Processing Laboratory Bâtiment MULTITEL/TCTS
Applied Optimization Application to Intensity-Modulated Radiation Therapy (IMRT)
 Applied Optimization Application to Intensity-Modulated Radiation Therapy (IMRT) 2008-05-08 Caroline Olsson, M.Sc. Topics Short history of radiotherapy Developments that has led to IMRT The IMRT process
Applied Optimization Application to Intensity-Modulated Radiation Therapy (IMRT) 2008-05-08 Caroline Olsson, M.Sc. Topics Short history of radiotherapy Developments that has led to IMRT The IMRT process
Basics of treatment planning II
 Basics of treatment planning II Sastry Vedam PhD DABR Introduction to Medical Physics III: Therapy Spring 2015 Monte Carlo Methods 1 Monte Carlo! Most accurate at predicting dose distributions! Based on
Basics of treatment planning II Sastry Vedam PhD DABR Introduction to Medical Physics III: Therapy Spring 2015 Monte Carlo Methods 1 Monte Carlo! Most accurate at predicting dose distributions! Based on
Automated segmentation methods for liver analysis in oncology applications
 University of Szeged Department of Image Processing and Computer Graphics Automated segmentation methods for liver analysis in oncology applications Ph. D. Thesis László Ruskó Thesis Advisor Dr. Antal
University of Szeged Department of Image Processing and Computer Graphics Automated segmentation methods for liver analysis in oncology applications Ph. D. Thesis László Ruskó Thesis Advisor Dr. Antal
Iterative regularization in intensity-modulated radiation therapy optimization. Carlsson, F. and Forsgren, A. Med. Phys. 33 (1), January 2006.
 Iterative regularization in intensity-modulated radiation therapy optimization Carlsson, F. and Forsgren, A. Med. Phys. 33 (1), January 2006. 2 / 15 Plan 1 2 3 4 3 / 15 to paper The purpose of the paper
Iterative regularization in intensity-modulated radiation therapy optimization Carlsson, F. and Forsgren, A. Med. Phys. 33 (1), January 2006. 2 / 15 Plan 1 2 3 4 3 / 15 to paper The purpose of the paper
IMRT and VMAT Patient Specific QA Using 2D and 3D Detector Arrays
 IMRT and VMAT Patient Specific QA Using 2D and 3D Detector Arrays Sotiri Stathakis Outline Why IMRT/VMAT QA AAPM TG218 UPDATE Tolerance Limits and Methodologies for IMRT Verification QA Common sources
IMRT and VMAT Patient Specific QA Using 2D and 3D Detector Arrays Sotiri Stathakis Outline Why IMRT/VMAT QA AAPM TG218 UPDATE Tolerance Limits and Methodologies for IMRT Verification QA Common sources
Position accuracy analysis of the stereotactic reference defined by the CBCT on Leksell Gamma Knife Icon
 Position accuracy analysis of the stereotactic reference defined by the CBCT on Leksell Gamma Knife Icon WHITE PAPER Introduction An image guidance system based on Cone Beam CT (CBCT) is included in Leksell
Position accuracy analysis of the stereotactic reference defined by the CBCT on Leksell Gamma Knife Icon WHITE PAPER Introduction An image guidance system based on Cone Beam CT (CBCT) is included in Leksell
An Optimisation Model for Intensity Modulated Radiation Therapy
 An Optimisation Model for Intensity Modulated Radiation Therapy Matthias Ehrgott Department of Engineering Science University of Auckland New Zealand m.ehrgott@auckland.ac.nz Abstract Intensity modulated
An Optimisation Model for Intensity Modulated Radiation Therapy Matthias Ehrgott Department of Engineering Science University of Auckland New Zealand m.ehrgott@auckland.ac.nz Abstract Intensity modulated
Applied Optimization: Application to Intensity-Modulated Radiation Therapy (IMRT)
 Applied Optimization: Application to Intensity-Modulated Radiation Therapy (IMRT) 2010-05-04 Caroline Olsson, M.Sc. caroline.olsson@vgregion.se Topics History of radiotherapy Developments that has led
Applied Optimization: Application to Intensity-Modulated Radiation Therapy (IMRT) 2010-05-04 Caroline Olsson, M.Sc. caroline.olsson@vgregion.se Topics History of radiotherapy Developments that has led
Advanced Targeting Using Image Deformation. Justin Keister, MS DABR Aurora Health Care Kenosha, WI
 Advanced Targeting Using Image Deformation Justin Keister, MS DABR Aurora Health Care Kenosha, WI History of Targeting The advance of IMRT and CT simulation has changed how targets are identified in radiation
Advanced Targeting Using Image Deformation Justin Keister, MS DABR Aurora Health Care Kenosha, WI History of Targeting The advance of IMRT and CT simulation has changed how targets are identified in radiation
Secondary 3D Dose QA Fully Automated using MOSAIQ's IQ Engine. MOSAIQ User Meeting May Antwerp
 Secondary 3D Dose QA Fully Automated using MOSAIQ's IQ Engine MOSAIQ User Meeting May 31 2013 - Antwerp Contents Project goal and collaboration Secondary 3D Dose QA project justification Secondary 3D Dose
Secondary 3D Dose QA Fully Automated using MOSAIQ's IQ Engine MOSAIQ User Meeting May 31 2013 - Antwerp Contents Project goal and collaboration Secondary 3D Dose QA project justification Secondary 3D Dose
Development and validation of clinically feasible 4D-MRI in radiotherapy
 MSc. Applied Physics Thesis Development and validation of clinically feasible 4D-MRI in radiotherapy Daniel Tekelenburg By: Daniel Ruphay Tekelenburg In partial fulfilment of the requirements for the degree
MSc. Applied Physics Thesis Development and validation of clinically feasible 4D-MRI in radiotherapy Daniel Tekelenburg By: Daniel Ruphay Tekelenburg In partial fulfilment of the requirements for the degree
Photon beam dose distributions in 2D
 Photon beam dose distributions in 2D Sastry Vedam PhD DABR Introduction to Medical Physics III: Therapy Spring 2014 Acknowledgments! Narayan Sahoo PhD! Richard G Lane (Late) PhD 1 Overview! Evaluation
Photon beam dose distributions in 2D Sastry Vedam PhD DABR Introduction to Medical Physics III: Therapy Spring 2014 Acknowledgments! Narayan Sahoo PhD! Richard G Lane (Late) PhD 1 Overview! Evaluation
ADVANCING CANCER TREATMENT
 3 ADVANCING CANCER TREATMENT SUPPORTING CLINICS WORLDWIDE RaySearch is advancing cancer treatment through pioneering software. We believe software has un limited potential, and that it is now the driving
3 ADVANCING CANCER TREATMENT SUPPORTING CLINICS WORLDWIDE RaySearch is advancing cancer treatment through pioneering software. We believe software has un limited potential, and that it is now the driving
Modern Medical Image Analysis 8DC00 Exam
 Parts of answers are inside square brackets [... ]. These parts are optional. Answers can be written in Dutch or in English, as you prefer. You can use drawings and diagrams to support your textual answers.
Parts of answers are inside square brackets [... ]. These parts are optional. Answers can be written in Dutch or in English, as you prefer. You can use drawings and diagrams to support your textual answers.
MINIMAX OPTIMIZATION FOR HANDLING RANGE AND SETUP UNCERTAINTIES IN PROTON THERAPY
 MINIMAX OPTIMIZATION FOR HANDLING RANGE AND SETUP UNCERTAINTIES IN PROTON THERAPY Albin FREDRIKSSON, Anders FORSGREN, and Björn HÅRDEMARK Technical Report TRITA-MAT-1-OS2 Department of Mathematics Royal
MINIMAX OPTIMIZATION FOR HANDLING RANGE AND SETUP UNCERTAINTIES IN PROTON THERAPY Albin FREDRIKSSON, Anders FORSGREN, and Björn HÅRDEMARK Technical Report TRITA-MAT-1-OS2 Department of Mathematics Royal
Is deformable image registration a solved problem?
 Is deformable image registration a solved problem? Marcel van Herk On behalf of the imaging group of the RT department of NKI/AVL Amsterdam, the Netherlands DIR 1 Image registration Find translation.deformation
Is deformable image registration a solved problem? Marcel van Herk On behalf of the imaging group of the RT department of NKI/AVL Amsterdam, the Netherlands DIR 1 Image registration Find translation.deformation
Dosimetric Analysis Report
 RT-safe 48, Artotinis str 116 33, Athens Greece +30 2107563691 info@rt-safe.com Dosimetric Analysis Report SAMPLE, for demonstration purposes only Date of report: ----------- Date of irradiation: -----------
RT-safe 48, Artotinis str 116 33, Athens Greece +30 2107563691 info@rt-safe.com Dosimetric Analysis Report SAMPLE, for demonstration purposes only Date of report: ----------- Date of irradiation: -----------
SUPPLEMENTARY INFORMATION
 SUPPLEMENTARY INFORMATION doi:10.1038/nature10934 Supplementary Methods Mathematical implementation of the EST method. The EST method begins with padding each projection with zeros (that is, embedding
SUPPLEMENTARY INFORMATION doi:10.1038/nature10934 Supplementary Methods Mathematical implementation of the EST method. The EST method begins with padding each projection with zeros (that is, embedding
Basics of treatment planning II
 Basics of treatment planning II Sastry Vedam PhD DABR Introduction to Medical Physics III: Therapy Spring 2015 Dose calculation algorithms! Correction based! Model based 1 Dose calculation algorithms!
Basics of treatment planning II Sastry Vedam PhD DABR Introduction to Medical Physics III: Therapy Spring 2015 Dose calculation algorithms! Correction based! Model based 1 Dose calculation algorithms!
Tomographic Reconstruction
 Tomographic Reconstruction 3D Image Processing Torsten Möller Reading Gonzales + Woods, Chapter 5.11 2 Overview Physics History Reconstruction basic idea Radon transform Fourier-Slice theorem (Parallel-beam)
Tomographic Reconstruction 3D Image Processing Torsten Möller Reading Gonzales + Woods, Chapter 5.11 2 Overview Physics History Reconstruction basic idea Radon transform Fourier-Slice theorem (Parallel-beam)
Whole Body MRI Intensity Standardization
 Whole Body MRI Intensity Standardization Florian Jäger 1, László Nyúl 1, Bernd Frericks 2, Frank Wacker 2 and Joachim Hornegger 1 1 Institute of Pattern Recognition, University of Erlangen, {jaeger,nyul,hornegger}@informatik.uni-erlangen.de
Whole Body MRI Intensity Standardization Florian Jäger 1, László Nyúl 1, Bernd Frericks 2, Frank Wacker 2 and Joachim Hornegger 1 1 Institute of Pattern Recognition, University of Erlangen, {jaeger,nyul,hornegger}@informatik.uni-erlangen.de
Joint CI-JAI advanced accelerator lecture series Imaging and detectors for medical physics Lecture 1: Medical imaging
 Joint CI-JAI advanced accelerator lecture series Imaging and detectors for medical physics Lecture 1: Medical imaging Dr Barbara Camanzi barbara.camanzi@stfc.ac.uk Course layout Day AM 09.30 11.00 PM 15.30
Joint CI-JAI advanced accelerator lecture series Imaging and detectors for medical physics Lecture 1: Medical imaging Dr Barbara Camanzi barbara.camanzi@stfc.ac.uk Course layout Day AM 09.30 11.00 PM 15.30
Fast 3D Mean Shift Filter for CT Images
 Fast 3D Mean Shift Filter for CT Images Gustavo Fernández Domínguez, Horst Bischof, and Reinhard Beichel Institute for Computer Graphics and Vision, Graz University of Technology Inffeldgasse 16/2, A-8010,
Fast 3D Mean Shift Filter for CT Images Gustavo Fernández Domínguez, Horst Bischof, and Reinhard Beichel Institute for Computer Graphics and Vision, Graz University of Technology Inffeldgasse 16/2, A-8010,
Machine Learning for Medical Image Analysis. A. Criminisi
 Machine Learning for Medical Image Analysis A. Criminisi Overview Introduction to machine learning Decision forests Applications in medical image analysis Anatomy localization in CT Scans Spine Detection
Machine Learning for Medical Image Analysis A. Criminisi Overview Introduction to machine learning Decision forests Applications in medical image analysis Anatomy localization in CT Scans Spine Detection
Robotics. Lecture 5: Monte Carlo Localisation. See course website for up to date information.
 Robotics Lecture 5: Monte Carlo Localisation See course website http://www.doc.ic.ac.uk/~ajd/robotics/ for up to date information. Andrew Davison Department of Computing Imperial College London Review:
Robotics Lecture 5: Monte Carlo Localisation See course website http://www.doc.ic.ac.uk/~ajd/robotics/ for up to date information. Andrew Davison Department of Computing Imperial College London Review:
ADAPTIVE TILE CODING METHODS FOR THE GENERALIZATION OF VALUE FUNCTIONS IN THE RL STATE SPACE A THESIS SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL
 ADAPTIVE TILE CODING METHODS FOR THE GENERALIZATION OF VALUE FUNCTIONS IN THE RL STATE SPACE A THESIS SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY BHARAT SIGINAM IN
ADAPTIVE TILE CODING METHODS FOR THE GENERALIZATION OF VALUE FUNCTIONS IN THE RL STATE SPACE A THESIS SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY BHARAT SIGINAM IN
TomoTherapy Related Projects. An image guidance alternative on Tomo Low dose MVCT reconstruction Patient Quality Assurance using Sinogram
 TomoTherapy Related Projects An image guidance alternative on Tomo Low dose MVCT reconstruction Patient Quality Assurance using Sinogram Development of A Novel Image Guidance Alternative for Patient Localization
TomoTherapy Related Projects An image guidance alternative on Tomo Low dose MVCT reconstruction Patient Quality Assurance using Sinogram Development of A Novel Image Guidance Alternative for Patient Localization
Implementation of the EGSnrc / BEAMnrc Monte Carlo code - Application to medical accelerator SATURNE43
 International Journal of Innovation and Applied Studies ISSN 2028-9324 Vol. 6 No. 3 July 2014, pp. 635-641 2014 Innovative Space of Scientific Research Journals http://www.ijias.issr-journals.org/ Implementation
International Journal of Innovation and Applied Studies ISSN 2028-9324 Vol. 6 No. 3 July 2014, pp. 635-641 2014 Innovative Space of Scientific Research Journals http://www.ijias.issr-journals.org/ Implementation
ELEC Dr Reji Mathew Electrical Engineering UNSW
 ELEC 4622 Dr Reji Mathew Electrical Engineering UNSW Review of Motion Modelling and Estimation Introduction to Motion Modelling & Estimation Forward Motion Backward Motion Block Motion Estimation Motion
ELEC 4622 Dr Reji Mathew Electrical Engineering UNSW Review of Motion Modelling and Estimation Introduction to Motion Modelling & Estimation Forward Motion Backward Motion Block Motion Estimation Motion
Interactive Deformable Registration Visualization and Analysis of 4D Computed Tomography
 Interactive Deformable Registration Visualization and Analysis of 4D Computed Tomography Burak Erem 1, Gregory C. Sharp 2, Ziji Wu 2, and David Kaeli 1 1 Department of Electrical and Computer Engineering,
Interactive Deformable Registration Visualization and Analysis of 4D Computed Tomography Burak Erem 1, Gregory C. Sharp 2, Ziji Wu 2, and David Kaeli 1 1 Department of Electrical and Computer Engineering,
VALIDATION OF A MONTE CARLO DOSE CALCULATION ALGORITHM FOR CLINICAL ELECTRON BEAMS IN THE PRESENCE OF PHANTOMS WITH COMPLEX HETEROGENEITIES
 VALIDATION OF A MONTE CARLO DOSE CALCULATION ALGORITHM FOR CLINICAL ELECTRON BEAMS IN THE PRESENCE OF PHANTOMS WITH COMPLEX HETEROGENEITIES by Shayla Landfair Enright A Thesis Submitted to the Faculty
VALIDATION OF A MONTE CARLO DOSE CALCULATION ALGORITHM FOR CLINICAL ELECTRON BEAMS IN THE PRESENCE OF PHANTOMS WITH COMPLEX HETEROGENEITIES by Shayla Landfair Enright A Thesis Submitted to the Faculty
7/31/2011. Learning Objective. Video Positioning. 3D Surface Imaging by VisionRT
 CLINICAL COMMISSIONING AND ACCEPTANCE TESTING OF A 3D SURFACE MATCHING SYSTEM Hania Al-Hallaq, Ph.D. Assistant Professor Radiation Oncology The University of Chicago Learning Objective Describe acceptance
CLINICAL COMMISSIONING AND ACCEPTANCE TESTING OF A 3D SURFACE MATCHING SYSTEM Hania Al-Hallaq, Ph.D. Assistant Professor Radiation Oncology The University of Chicago Learning Objective Describe acceptance
gpmc: GPU-Based Monte Carlo Dose Calculation for Proton Radiotherapy Xun Jia 8/7/2013
 gpmc: GPU-Based Monte Carlo Dose Calculation for Proton Radiotherapy Xun Jia xunjia@ucsd.edu 8/7/2013 gpmc project Proton therapy dose calculation Pencil beam method Monte Carlo method gpmc project Started
gpmc: GPU-Based Monte Carlo Dose Calculation for Proton Radiotherapy Xun Jia xunjia@ucsd.edu 8/7/2013 gpmc project Proton therapy dose calculation Pencil beam method Monte Carlo method gpmc project Started
ADVANCING CANCER TREATMENT
 The RayPlan treatment planning system makes proven, innovative RayStation technology accessible to clinics that need a cost-effective and streamlined solution. Fast, efficient and straightforward to use,
The RayPlan treatment planning system makes proven, innovative RayStation technology accessible to clinics that need a cost-effective and streamlined solution. Fast, efficient and straightforward to use,
Image Guidance and Beam Level Imaging in Digital Linacs
 Image Guidance and Beam Level Imaging in Digital Linacs Ruijiang Li, Ph.D. Department of Radiation Oncology Stanford University School of Medicine 2014 AAPM Therapy Educational Course Disclosure Research
Image Guidance and Beam Level Imaging in Digital Linacs Ruijiang Li, Ph.D. Department of Radiation Oncology Stanford University School of Medicine 2014 AAPM Therapy Educational Course Disclosure Research
Applied Optimization Application to Intensity-Modulated Radiation Therapy (IMRT)
 Applied Optimization Application to Intensity-Modulated Radiation Therapy (IMRT) 2009-05-08 Caroline Olsson, M.Sc. Topics History of radiotherapy Developments that has led to IMRT The IMRT process How
Applied Optimization Application to Intensity-Modulated Radiation Therapy (IMRT) 2009-05-08 Caroline Olsson, M.Sc. Topics History of radiotherapy Developments that has led to IMRT The IMRT process How
Bootstrapping Method for 14 June 2016 R. Russell Rhinehart. Bootstrapping
 Bootstrapping Method for www.r3eda.com 14 June 2016 R. Russell Rhinehart Bootstrapping This is extracted from the book, Nonlinear Regression Modeling for Engineering Applications: Modeling, Model Validation,
Bootstrapping Method for www.r3eda.com 14 June 2016 R. Russell Rhinehart Bootstrapping This is extracted from the book, Nonlinear Regression Modeling for Engineering Applications: Modeling, Model Validation,
OPTIMIZATION METHODS IN INTENSITY MODULATED RADIATION THERAPY TREATMENT PLANNING
 OPTIMIZATION METHODS IN INTENSITY MODULATED RADIATION THERAPY TREATMENT PLANNING By DIONNE M. ALEMAN A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT
OPTIMIZATION METHODS IN INTENSITY MODULATED RADIATION THERAPY TREATMENT PLANNING By DIONNE M. ALEMAN A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT
Mathematical methods and simulations tools useful in medical radiation physics
 Mathematical methods and simulations tools useful in medical radiation physics Michael Ljungberg, professor Department of Medical Radiation Physics Lund University SE-221 85 Lund, Sweden Major topic 1:
Mathematical methods and simulations tools useful in medical radiation physics Michael Ljungberg, professor Department of Medical Radiation Physics Lund University SE-221 85 Lund, Sweden Major topic 1:
An optimization framework for conformal radiation treatment planning
 An optimization framework for conformal radiation treatment planning Jinho Lim Michael C. Ferris Stephen J. Wright David M. Shepard Matthew A. Earl December 2002 Abstract An optimization framework for
An optimization framework for conformal radiation treatment planning Jinho Lim Michael C. Ferris Stephen J. Wright David M. Shepard Matthew A. Earl December 2002 Abstract An optimization framework for
Probability and Statistics for Final Year Engineering Students
 Probability and Statistics for Final Year Engineering Students By Yoni Nazarathy, Last Updated: April 11, 2011. Lecture 1: Introduction and Basic Terms Welcome to the course, time table, assessment, etc..
Probability and Statistics for Final Year Engineering Students By Yoni Nazarathy, Last Updated: April 11, 2011. Lecture 1: Introduction and Basic Terms Welcome to the course, time table, assessment, etc..
Prof. Fanny Ficuciello Robotics for Bioengineering Visual Servoing
 Visual servoing vision allows a robotic system to obtain geometrical and qualitative information on the surrounding environment high level control motion planning (look-and-move visual grasping) low level
Visual servoing vision allows a robotic system to obtain geometrical and qualitative information on the surrounding environment high level control motion planning (look-and-move visual grasping) low level
Radiation Therapy Planning by Multicriteria Optimisation
 Radiation Therapy Planning by Multicriteria Optimisation Matthias Ehrgott, Mena Burjony Deptartment of Engineering Science University of Auckland New Zealand m.ehrgott@auckland.ac.nz Abstract Radiation
Radiation Therapy Planning by Multicriteria Optimisation Matthias Ehrgott, Mena Burjony Deptartment of Engineering Science University of Auckland New Zealand m.ehrgott@auckland.ac.nz Abstract Radiation
Improvement and Evaluation of a Time-of-Flight-based Patient Positioning System
 Improvement and Evaluation of a Time-of-Flight-based Patient Positioning System Simon Placht, Christian Schaller, Michael Balda, André Adelt, Christian Ulrich, Joachim Hornegger Pattern Recognition Lab,
Improvement and Evaluation of a Time-of-Flight-based Patient Positioning System Simon Placht, Christian Schaller, Michael Balda, André Adelt, Christian Ulrich, Joachim Hornegger Pattern Recognition Lab,
1. Learn to incorporate QA for surface imaging
 Hania Al-Hallaq, Ph.D. Assistant Professor Radiation Oncology The University of Chicago ***No disclosures*** 1. Learn to incorporate QA for surface imaging into current QA procedures for IGRT. 2. Understand
Hania Al-Hallaq, Ph.D. Assistant Professor Radiation Oncology The University of Chicago ***No disclosures*** 1. Learn to incorporate QA for surface imaging into current QA procedures for IGRT. 2. Understand
Supplementary Figure 1. Decoding results broken down for different ROIs
 Supplementary Figure 1 Decoding results broken down for different ROIs Decoding results for areas V1, V2, V3, and V1 V3 combined. (a) Decoded and presented orientations are strongly correlated in areas
Supplementary Figure 1 Decoding results broken down for different ROIs Decoding results for areas V1, V2, V3, and V1 V3 combined. (a) Decoded and presented orientations are strongly correlated in areas
Combination of Markerless Surrogates for Motion Estimation in Radiation Therapy
 Combination of Markerless Surrogates for Motion Estimation in Radiation Therapy CARS 2016 T. Geimer, M. Unberath, O. Taubmann, C. Bert, A. Maier June 24, 2016 Pattern Recognition Lab (CS 5) FAU Erlangen-Nu
Combination of Markerless Surrogates for Motion Estimation in Radiation Therapy CARS 2016 T. Geimer, M. Unberath, O. Taubmann, C. Bert, A. Maier June 24, 2016 Pattern Recognition Lab (CS 5) FAU Erlangen-Nu
Cpk: What is its Capability? By: Rick Haynes, Master Black Belt Smarter Solutions, Inc.
 C: What is its Capability? By: Rick Haynes, Master Black Belt Smarter Solutions, Inc. C is one of many capability metrics that are available. When capability metrics are used, organizations typically provide
C: What is its Capability? By: Rick Haynes, Master Black Belt Smarter Solutions, Inc. C is one of many capability metrics that are available. When capability metrics are used, organizations typically provide
Ch. 4 Physical Principles of CT
 Ch. 4 Physical Principles of CT CLRS 408: Intro to CT Department of Radiation Sciences Review: Why CT? Solution for radiography/tomography limitations Superimposition of structures Distinguishing between
Ch. 4 Physical Principles of CT CLRS 408: Intro to CT Department of Radiation Sciences Review: Why CT? Solution for radiography/tomography limitations Superimposition of structures Distinguishing between
