UCLA STAT 13 Introduction to Statistical Methods for the Life and Health Sciences
|
|
|
- Madlyn Lee
- 5 years ago
- Views:
Transcription
1 UCLA STAT 3 Introduction to Statistical Methods for the Life and Health Sciences!Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology!Teaching Assistants: Ming heng, Annie Che UCLA Statistics Chapter 6: Continuous Random Variables!Continuous Random Variables!The Normal Distribution!Sums and differences of random quantities University of California, Los Angeles, Winter Slide Slide Dietary intake of carbohydrate (mg/day) for N=599 people from a variety of work environments. Standardized histogram plot is unimodal but skewed to the right (high values). Vertical scale is (relative freq.)/(interval width) = f j /(N*m). The proportion of the data in [a : b] is the area under the standardized histogram on the range [a: b]. Superposition of a smooth curve (density function) on the standardized histogram (left panel). under the density curve on [a: b] = [5: 375] is analytically computed to be: (right panel), which is close to the empirically obtained estimate of the area under the histogram on the same interval: (left panel). (a) Standardized histogram (b) between a = 5 and b = 375 shaded (c) With approximating curve (d) between a = 5 and b = 375 shaded Shaded area =.483 (Corresponds to 48.3% of observations) Shaded area =.486 (cf. area =.483 for histogram) m 375 Carbohydrate (mg/day) Slide Carbohydrate (mg/day) Slide 4 Standardized histograms Probability and areas For a standardized histogram:.00! The vertical scale is Carbohydrate (mg/day) Relative_frequency / Interval_width! Total area under histogram =! Proportion of the data between a and b is the area under histogram between a and b For a continuous X.00 (d) between a = 5 and b = 375 shaded Shaded area =.486 (cf. area =.483 for histogram) ! the probability a random observation falls between a and b = area under the density curve between a and b. Slide 5 Slide 6
2 Sampling from the distribution in Fig. 6.. (b) Histograms with density curve superimposed (a) Dot plots of 6 sets of 5 random observations 6 sets of samples of 5 obs s observations 50,000 observations ,000 observations 5 million observations Note the fair amount of intra- and intergroup variability. What does that mean? Is that normal or expected? Slide From Chance Encounters by C.J. Wild and G.A.F. Seber, John Wiley & Sons, 000. Slide Visualizing the population mean Interval endpoints and continuous variables X Recall a continuous variable is one where the domain has no gaps in between the values the variable can take. In calculations involving a continuous random variable we do not have to worry about whether interval endpoints are included or excluded. The population mean is the imaginary value of X where the density curve balances Slide 0 Slide Review Review! How does a standardized histogram differ from a relative-frequency histogram? raw histogram? (f j /mn)! What graphic feature conveys the proportion of the data falling into a class interval for a standardized histogram? for a relative-frequency histogram? (area=width. height = m f j /mn= f j /n)! What are the two fundamental ways in which random observations arise? (Natural phenomena, sampling experiments choose a student at random and use the lottery method to record characteristics, scientific experiments - blood pressure measure)! How does a density curve describe probabilities? (The probability that a random obs. falls in [a:b] is the area under the PDF on the same interval.)! What is the total area under both a standardized histogram and a probability density curve? ()! When can histograms of data from a random process be relied on to closely resemble the density curve for that process? (large sample size, small histogram bin-size)! What characteristic of the density curve does the mean correspond to? (imaginary value of X, where the density curve balances) Slide Slide 3
3 Review! Does it matter whether interval endpoints are included or excluded when we calculate probabilities for a continuous random variable from the area? (No) Two standardized histograms with approximating Normal density curve Normal density curve has = 39.8 in., =.05 in (a) Chest measurements of Quetelet s Scottish soldiers (in.)! Why? ([a:b] == (a:b))! Are discrete variables the same or different in this regard, interval endpoint not effecting the area? (Different) Normal density curve has = 74 cm, = 6.57 cm Slide (b) Heights of the 494 men in the workforce database (cm) Slide 5 The Normal distribution density curve! Is symmetric about the mean! Bell-shaped and unimodal.! Mean = Median! (a) Changing shifts the curve along the axis Effects of µ and σ = = 6 Mean is a measure of central tendency (b) Increasing. N(µ, σ) 50% 50% Mean Slide = 60 =74 Standard deviation is a measure of variability/spread increases the spread and flattens the curve Slide 7 = 6 = = =70 Understanding the standard deviation: σ Probabilities supplied by computer programs Cumulative (lower-tail) probabilities = pr (X x ) = pr (X x ) Probabilities/areas (c) and numbers and numbers of standard of deviations standard deviations for the Normal distribution Shaded area = Shaded area = Shaded area = x OR x s in [0:] of the Std.Normal Distribution Are obtained by STATA command ztable % chance of falling 95% chance of falling between and + between and % chance of falling between 3 and + 3 Slide 8 Slide 9 3
4 Probabilities supplied by computer programs Cumulative (lower-tail) probabilities Problem:To find P(X<=80), when µ=74 and σ=6.57 Convert to Standard units: Y = (X- µ)/ σ = 6/6.57 = 0.9 Look-up the Normal Distribution Table: Final cumulative (lower-tail) result: = 0.89 = pr (X x ) Finding Help with STATA! /STAT3_Fall0/STAT3_labs.html OR Slide 0 Slide Basic method for obtaining probabilities (a) Computing pr(60 < X 80)! Sketch a Normal curve, marking the mean and other values of interest.! Shade the area under the curve that gives the desired probability.! Devise a way of getting the desired area from lowertail areas.! Obtain component lower-tail probabilities from a computer program Programs supply pr(x 80) and pr(x 60) pr(60 < X 80) = difference Shaded area =74 80 Shaded area 60 =74 We want Shaded area 60 =74 80 pr(60 < X 80) = pr(x 80) pr(x 60) Slide Slide 3 Fig. 6..4(c) Obtaining an upper-tail probability b Note: pr(x b) (c) More Normal probabilities (values obtained from Minitab) a pr(x a) pr(a < X b) = difference cm = 5ft, 67.6cm = 5ft 6in., 77.8cm = 5ft 0in., 8.9cm = 6ft From Chance Encounters by C.J. Wild and G.A.F. Seber, John Wiley & Sons, 000. We want Programs supply pr(x > 5) pr(x 5) pr(x > 5) =?? = =7. 5 =7. Since total area under curve =, pr(x > 5) = - pr(x 5) Generally, pr(x > x) = - pr(x x) Slide 4 Slide 5 4
5 Review Review! What features of the Normal curve do µ and σ visually correspond to? (point-of-balance; width/spread)! What is the probability that a random observation from a normal distribution is smaller than the mean? (0.5) larger than the mean? (0.5) exactly equal to the mean? (0.0) Why?! Approximately, what is the probability that a random observation from a normal distribution falls within standard deviation (SD) of the mean? (0.68) SD's? (0.95) 3 SD's? (0.997)! Computer programs may provide cumulative or partial probabilities for the normal distribution. What is a the difference between these? Can we get one from the other? Slide 6 Slide 7 The inverse problem Percentiles/quantiles prob = p (a) p-quantile Programs supply x p x-value for which pr(x x =?? p x ) = p p (b) 80th percentile (0.8-quantile) of women s heights prob = 0.8 Normal( = 6.7, = 6.) =6.7 x 0.8=?? Program returns Thus 80% lie below % of people have height below the 80th percentile. This is EQ to saying there s 80% chance that a random observation from the distribution (c) Further percentiles of women s heights Percent % 5% 0% 0% 30% 70% 80% 90% 95% 99% Propn Percentile (cm) (or quantile) (ft'in") 4'0" 5'0" 5'0" 5'" 5'" 5'5" 5'6" 5'7" 5'8 5'9" (+ frac) 3/8" 7/8" 3/4" 3/8" /8" /8" /8" 3/4" The inverse problem is what is the height for the 80th percentile/quantile? So far we studied given the height value what s the corresponding percentile? Slide 8 will fall below the 80th percentile. What value gives the top 5%? =6.7 The inverse problem upper-tail percentiles/quantiles Obtaining an inverse upper-tail probability??? What does this say about the lower tail? 0.5 prob = 0.5 Obtain from program Slide 9 prob = =6.7??? 0.5 [ Program returns 66.88] prob Review Standard Normal Curve! What is meant by the 60th percentile of heights?! What is the difference between a percentile and a quantile? (percentile used in expressing results in %, whereas quantiles used to express results in term of probabilities)! The lower quartile, median and upper quartile of a distribution correspond to special percentiles. What are they? express in terms of quantiles. (5%, 50%, 75%)! Quantiles are sometimes called inverse cumulative probabilities. Why?! The standard normal curve is described by the equation: y = x e π Where remember, the natural number e ~.78 We say: X~Normal(µ, σ), or simply X~N(µ, σ) Slide 30 Slide 3 5
6 Standard Normal Approximation General Normal Curve! The standard normal curve can be used to estimate the percentage of entries in an interval for any process. Here is the protocol for this approximation: " Convert the interval (we need the assess the percentage of entries in) to standard units. We saw the algorithm already. " Find the corresponding area under the normal curve (from tables or online databases); Data 8 Transform to Std.Units What percentage of the density scale histogram is shown on this graph? Report back % Slide 3 Compute %! The general normal curve is defined by: " Where µ is the average of (the symmetric) normal curve, and σ is the standard deviation (spread of the distribution). " Why worry about a standard and general normal curves? " How to convert between the two curves? Slide 33 y = ( x ) µ σ e πσ s under Standard Normal Curve Normal Approximation! Protocol: " Convert the interval (we need to assess the percentage of entries in) to Standard units. Actually convert the end points in Standard units. #In general, the transformation X $ (X-µ)/σ, standardizes the observed value X, where µ and σ are the average and the standard deviation of the distribution X is drawn from. " Find the corresponding area under the normal curve (from tables or online databases); #Sketch the normal curve and shade the area of interest #Separate your area into individually computable sections #Check the Normal Table and extract the areas of every subsection #Add/compute the areas of all sub-sections to get the total area. Slide 34 The central 50% Obtaining central range for symmetric distributions 0.5 a =?? 6.7 b =?? What values contain the central 50%? What does that say about the lower tails? a =?? 6.7 b =?? a =?? 6.7 Obtain a from program Slide b =?? Obtain b from program The z-score The standard Normal distribution! The z-score of x is the number of standard deviations x is from the mean. (Body-Mass-Index, BMI) TABLE 6.3. Examples of z -Scores X z -score = (x - µ )/σ Interpretation Male BMI values (kg/m ) 5 (5-7.3)/4. = kg/m is 0.56 sd's below the mean 35 (35-7.3)/4. = kg/m is.88 sd's above the mean Female heights (cm) 55 (55-6.7)/6. = cm is.4 sd's below the mean 80 (80-6.7)/6. =.79 80cm is.79 sd's above the mean Male BMI-values: µ =7.3, σ =4. Females heights: µ=6.7, σ=6.! Which ones of these are unusually large/small/away from the mean? Standard Normal distribution: mean(µ) = 0, SD(σ)= Slide 36 Slide 37 6
7 The central 90% Working in standard units What values contain the central 90%? What does that say about the lower tail? Working in standard units (# of SD s) TABLE 6.3. Central Ranges Male BMI values Female heights -z 90% 5% 90% 5% 0 z =?? -z 95% 0 0 z =?? -z z =?? Obtain z from program [Program returns.6449]! The z-score of x is the number of standard deviations x is away from the mean. Percentage z µ - z σ µ + z σ µ - z σ µ + z σ 80% % % % % Standardizing = ( X µ ) / M a le B M I-value s : µ=7.3, σ=4. Females heights : Inverting µ=6.7, σ=6. X = σ + µ σ Slide 38 Slide 40 TABLE Using z -score tables As an example, we shall find pr(.357) using part of the table given in Appendix A4 (reproduced below). Quincunx Step : Correct the z -value to two decimal places, that is, use z =.4. Step : Look down the z column until you find.. This tells you which row to look in. Step 3: The second decimal place, here 4, tells you which column to look in. Step 4: The entry in the table corresponding to that row and column is pr(.4) = z Slide 4 Slide 4 Continuous Variables and Density Curves The density curve! There are no gaps between the values a continuous random variable can take.! Random observations arise in two main ways: (i) by sampling populations; and (ii) by observing processes.! The probability distribution of a continuous variable is represented by a density curve. " Probabilities are represented by areas under the curve, #the probability that a random observation falls between a and b equal to the area under the density curve between a and b. " The total area under the curve equals. " The population (or distribution) mean µ X = E(X), is where the density curve balances. " When we calculate probabilities for a continuous random variable, it does not matter whether interval endpoints are included or excluded. Slide 43 Slide 44 7
8 For any random variable X The Normal distribution! E(aX +b) = a E(X) +b and SD(aX +b) = a SD(X) X ~ Normal(µ x = µ, σ x = σ) Features of the Normal density curve:! The curve is a symmetric bell-shape centered at µ.! The standard deviation σ governs the spread. " 68.3% of the probability lies within standard deviation of the mean " 95.4% within standard deviations " 99.7% within 3 standard deviations Slide 45 Slide 46 Probabilities! Computer programs provide lower-tail (or cumulative) probabilities of the form pr(x x) " We give the program the x-value; it gives us the probability.! Computer programs also provide inverse lower-tail probabilities (or quantiles) " We give the program the probability; it gives us the x- value.! When calculating probabilities, we shade the desired area under the curve and then devise a way of obtaining it via lower-tail probabilities. Slide 47 Standard Units The z-score of a value a is.! the number of standard deviations a is away from the mean! positive if a is above the mean and negative if a is below the mean. The standard Normal distribution has µ = 0 and σ = 0.! We usually use to represent a random variable with a standard Normal distribution. Slide 48 Ranges, extremes and z-scores Combining Random Quantities Central ranges: " P(-z z) is the same as the probability that a random observation from an arbitrary Normal distribution falls within z SD's either side of the mean. Extremes: " P( z) is the same as the probability that a random observation from an arbitrary Normal distribution falls more than z standard deviations above the mean. " P( -z) is the same as the probability that a random observation from an arbitrary Normal distribution falls more than z standard deviations below the mean. Variation and independence:! No two animals, organisms, natural or man-made objects are ever identical.! There is always variation. The only question is whether it is large enough to have a practical impact on what you are trying to achieve.! Variation in component parts leads to even greater variation in the whole. Slide 49 Slide 50 8
9 Independence We model variables as being independent.! if we think they relate to physically independent processes! and if we have no data that suggests they are related. Both sums and differences of independent random variables are more variable than any of the component random variables Formulas! For a constant number a, E(aX) = ae(x) and SD(aX) = a SD(X).! Means of sums and differences of random variables act in an obvious way " the mean of the sum is the sum of the means " the mean of the difference is the difference in the means! For independent random variables, (cf. Pythagorean theorem), SD( X + = SD( X = SD( + SD( E( X + = E( + E( [ASIDE: Sums and differences of independent Normally distributed random variables are also Normally distributed] Slide 5 Slide 5 Example Example! Assumption: Crime rate for individuals is independent of family relations!! Let X = RV representing the number of crimes an average individual commits in a 5 yr span.! Let X and X be the crime rates of a husband and the wife in one family. What is the expected crime rate for this family given that E(X) =.4 and SD(X) = 0.7? SD( X + = SD( X = SD( + SD( E( X + = E( + E(! Assumption: Crime rate for individuals is independent of family relations!! If X+X = 3X-, dependent case! X and X are independent (family relation)! Suppose X+X = 5, is this atypical? SD( X + = SD( X = E( X + = E( + E( SD( + SD( Slide 53 Slide 54 s under Standard Normal Curve Normal Approximation! Protocol: " Convert the interval (we need to assess the percentage of entries in) to Standard units. Actually convert the end points in Standard units. #In general, the transformation X $ (X-µ)/σ, standardizes the observed value X, where µ and σ are the average and the standard deviation of the distribution X is drawn from. " Find the corresponding area under the normal curve (from tables or online databases); #Sketch the normal curve and shade the area of interest #Separate your area into individually computable sections #Check the Normal Table and extract the areas of every subsection #Add/compute the areas of all sub-sections to get the total area. s under Standard Normal Curve Normal Approximation, Scottish Army Recruits! The mean height is 64 in and the standard deviation is in. " Only recruits shorter than 65.5 in will be trained for tank operation. What percentage of the incoming recruits will be trained to operate armored combat vehicles (tanks)? X $ (X-64)/ 65.5 $ ( )/ = ¾ Percentage is 77.34% " Recruits within ½ standard deviations of the mean will have no restrictions on duties. About what percentage of the recruits will have no restrictions on training/duties? X $ (X-64)/ 65 $ (65-64)/ = ½ 63 $ (63-64)/ = -½ Percentage is 38.30% Slide 55 Slide 56 9
10 Percentiles for Standard Normal Curve! When the histogram of the observed process follows the normal curve Normal Tables (of any type, as described before) may be used to estimate percentiles. The N-th percentile of a distribution is P is N% of the population observations are less than or equal to P.! Example, suppose the Math-part SAT scores of newly admitted freshmen at UCLA averaged 535 (out of [00:800]) and the SD was 00. Estimate the 95 percentile for the score distribution.! Solution: 95% 90% % 5% -z z=? Slide 57 95% =? Percentiles for Standard Normal Curve! Example, suppose the Math-part SAT scores of newly admitted freshmen at UCLA averaged 535 (out of [00:800]) and the SD was 00. Estimate the 95 percentile for the score distribution.! Solution: 95% 90% % 5% -z z=? ! =.65 (std. Units) $ 700 (data units), since X $ (X µ)/σ, converts data to standard units and X $ σ X + µ, converts standard to data units! σ = 00; µ =535, 00 x = 700. Slide 58 95% =? Summary. The Standard Normal curve is symmetric w.r.t. the origin (0,0) and the total area under the curve is 00% ( unit). Std units indicate how many SD s is a value below (-)/above (+) the mean 3. Many histograms have roughly the shape of the normal curve (bellshape) 4. If a list of numbers follows the normal curve the percentage of entries falling within each interval is estimated by:. Converting the interval to StdUnits and,. Computing the corresponding area under the normal curve (Normal approximation) 5. A histogram which follows the normal curve may be reconstructed just from (µ,σ ), mean and variance=std_dev 6. Any histogram can be summarized using percentiles 7. E(aX+b)=aE(X)+b, Var(aX+b)=a Var(X), where E(Y) the the mean of Y and Var(Y) is the square of the StdDev(Y), Example work out in your notebooks. Compute the chance a random observation from a distribution (symmetric, bell-shaped, unimodal) with m=75 and SD= falls within the range [53 : 7]. Check Work Should it be <50% or >50%? b a 9 b Slide 59 Slide 60 Example work out in your notebooks Compute the chance a random observation from a distribution (symmetric, bellshaped & unimodal) with mean µ=75 and SD σ=, falls within the range [53 : 7].. (53-75)/ = -/6=-.83 Std unit Check Work. (7-75)/=-0.333(3) Std units Should it be <50% or >50%? 3. [53:7] = 4. (SN_area[-.83 : 0] SN_area[-0.33 : 0]) = ( ) = 0.34 (34%) 6. Compute the 90 th percentile for the same data: 7. b+a+c=00% a=40% c b a 8. b=50% c=0% =.8 SU 9. 90% Percentile = σ.3 + µ =x.8+75 = General Normal Curve! The general normal curve is defined by: " Where µ is the average of (the symmetric) normal curve, and σ is the standard deviation (spread of the distribution). " Why worry about a standard and general normal curves? " How to convert between the two curves? y = ( x ) µ σ e πσ Slide 6 Slide 6 0
11 s under Standard Normal Curve Standard Normal Curve Table differences! Many histograms are similar in shape to the standard normal curve. For example, persons height. The height of all incoming female army recruits is measured for custom training and assignment purposes (e.g., very tall people are inappropriate for constricted space positions, and very short people may be disadvantages in certain other situations). The mean height is computed to be 64 in and the standard deviation is in. Only recruits shorter than 65.5 in will be trained for tank operation and recruits within ½ standard deviations of the mean will have no restrictions on duties. " What percentage of the incoming recruits will be trained to operate armored combat vehicles (tanks)? " About what percentage of the recruits will have no restrictions on training/duties? Slide 63! There are different tables and computer packages for representing the area under the standard normal curve. But the results are always interchangeable. under Normal curve on [-z : z] z 0 z under Normal curve on [z: infinity] under Normal curve on [-infinity : z] Slide z STAT 3, 0 UCLA, z Ivo Dinov Standard Normal Curve Table differences! There are different tables and computer packages for representing the area under the standard normal curve. But the results are always interchangeable. under Normal curve on [-z : z] under Normal curve on [-infinity : z] z 0 z 0 z under Normal curve on [0 : z] Slide 65 STAT 3, 0 UCLA, z Ivo Dinov
Density Curve (p52) Density curve is a curve that - is always on or above the horizontal axis.
 1.3 Density curves p50 Some times the overall pattern of a large number of observations is so regular that we can describe it by a smooth curve. It is easier to work with a smooth curve, because the histogram
1.3 Density curves p50 Some times the overall pattern of a large number of observations is so regular that we can describe it by a smooth curve. It is easier to work with a smooth curve, because the histogram
Lecture 3 Questions that we should be able to answer by the end of this lecture:
 Lecture 3 Questions that we should be able to answer by the end of this lecture: Which is the better exam score? 67 on an exam with mean 50 and SD 10 or 62 on an exam with mean 40 and SD 12 Is it fair
Lecture 3 Questions that we should be able to answer by the end of this lecture: Which is the better exam score? 67 on an exam with mean 50 and SD 10 or 62 on an exam with mean 40 and SD 12 Is it fair
Chapter 5: The standard deviation as a ruler and the normal model p131
 Chapter 5: The standard deviation as a ruler and the normal model p131 Which is the better exam score? 67 on an exam with mean 50 and SD 10 62 on an exam with mean 40 and SD 12? Is it fair to say: 67 is
Chapter 5: The standard deviation as a ruler and the normal model p131 Which is the better exam score? 67 on an exam with mean 50 and SD 10 62 on an exam with mean 40 and SD 12? Is it fair to say: 67 is
Lecture 3 Questions that we should be able to answer by the end of this lecture:
 Lecture 3 Questions that we should be able to answer by the end of this lecture: Which is the better exam score? 67 on an exam with mean 50 and SD 10 or 62 on an exam with mean 40 and SD 12 Is it fair
Lecture 3 Questions that we should be able to answer by the end of this lecture: Which is the better exam score? 67 on an exam with mean 50 and SD 10 or 62 on an exam with mean 40 and SD 12 Is it fair
appstats6.notebook September 27, 2016
 Chapter 6 The Standard Deviation as a Ruler and the Normal Model Objectives: 1.Students will calculate and interpret z scores. 2.Students will compare/contrast values from different distributions using
Chapter 6 The Standard Deviation as a Ruler and the Normal Model Objectives: 1.Students will calculate and interpret z scores. 2.Students will compare/contrast values from different distributions using
STA Module 4 The Normal Distribution
 STA 2023 Module 4 The Normal Distribution Learning Objectives Upon completing this module, you should be able to 1. Explain what it means for a variable to be normally distributed or approximately normally
STA 2023 Module 4 The Normal Distribution Learning Objectives Upon completing this module, you should be able to 1. Explain what it means for a variable to be normally distributed or approximately normally
STA /25/12. Module 4 The Normal Distribution. Learning Objectives. Let s Look at Some Examples of Normal Curves
 STA 2023 Module 4 The Normal Distribution Learning Objectives Upon completing this module, you should be able to 1. Explain what it means for a variable to be normally distributed or approximately normally
STA 2023 Module 4 The Normal Distribution Learning Objectives Upon completing this module, you should be able to 1. Explain what it means for a variable to be normally distributed or approximately normally
Prepare a stem-and-leaf graph for the following data. In your final display, you should arrange the leaves for each stem in increasing order.
 Chapter 2 2.1 Descriptive Statistics A stem-and-leaf graph, also called a stemplot, allows for a nice overview of quantitative data without losing information on individual observations. It can be a good
Chapter 2 2.1 Descriptive Statistics A stem-and-leaf graph, also called a stemplot, allows for a nice overview of quantitative data without losing information on individual observations. It can be a good
Chapter 2 Modeling Distributions of Data
 Chapter 2 Modeling Distributions of Data Section 2.1 Describing Location in a Distribution Describing Location in a Distribution Learning Objectives After this section, you should be able to: FIND and
Chapter 2 Modeling Distributions of Data Section 2.1 Describing Location in a Distribution Describing Location in a Distribution Learning Objectives After this section, you should be able to: FIND and
Chapter 1. Looking at Data-Distribution
 Chapter 1. Looking at Data-Distribution Statistics is the scientific discipline that provides methods to draw right conclusions: 1)Collecting the data 2)Describing the data 3)Drawing the conclusions Raw
Chapter 1. Looking at Data-Distribution Statistics is the scientific discipline that provides methods to draw right conclusions: 1)Collecting the data 2)Describing the data 3)Drawing the conclusions Raw
IT 403 Practice Problems (1-2) Answers
 IT 403 Practice Problems (1-2) Answers #1. Using Tukey's Hinges method ('Inclusionary'), what is Q3 for this dataset? 2 3 5 7 11 13 17 a. 7 b. 11 c. 12 d. 15 c (12) #2. How do quartiles and percentiles
IT 403 Practice Problems (1-2) Answers #1. Using Tukey's Hinges method ('Inclusionary'), what is Q3 for this dataset? 2 3 5 7 11 13 17 a. 7 b. 11 c. 12 d. 15 c (12) #2. How do quartiles and percentiles
Stat 528 (Autumn 2008) Density Curves and the Normal Distribution. Measures of center and spread. Features of the normal distribution
 Stat 528 (Autumn 2008) Density Curves and the Normal Distribution Reading: Section 1.3 Density curves An example: GRE scores Measures of center and spread The normal distribution Features of the normal
Stat 528 (Autumn 2008) Density Curves and the Normal Distribution Reading: Section 1.3 Density curves An example: GRE scores Measures of center and spread The normal distribution Features of the normal
BIOL Gradation of a histogram (a) into the normal curve (b)
 (التوزيع الطبيعي ( Distribution Normal (Gaussian) One of the most important distributions in statistics is a continuous distribution called the normal distribution or Gaussian distribution. Consider the
(التوزيع الطبيعي ( Distribution Normal (Gaussian) One of the most important distributions in statistics is a continuous distribution called the normal distribution or Gaussian distribution. Consider the
Chapter 6. THE NORMAL DISTRIBUTION
 Chapter 6. THE NORMAL DISTRIBUTION Introducing Normally Distributed Variables The distributions of some variables like thickness of the eggshell, serum cholesterol concentration in blood, white blood cells
Chapter 6. THE NORMAL DISTRIBUTION Introducing Normally Distributed Variables The distributions of some variables like thickness of the eggshell, serum cholesterol concentration in blood, white blood cells
Chapter 5. Normal. Normal Curve. the Normal. Curve Examples. Standard Units Standard Units Examples. for Data
 curve Approximation Part II Descriptive Statistics The Approximation Approximation The famous normal curve can often be used as an 'ideal' histogram, to which histograms for data can be compared. Its equation
curve Approximation Part II Descriptive Statistics The Approximation Approximation The famous normal curve can often be used as an 'ideal' histogram, to which histograms for data can be compared. Its equation
Distributions of random variables
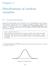 Chapter 3 Distributions of random variables 31 Normal distribution Among all the distributions we see in practice, one is overwhelmingly the most common The symmetric, unimodal, bell curve is ubiquitous
Chapter 3 Distributions of random variables 31 Normal distribution Among all the distributions we see in practice, one is overwhelmingly the most common The symmetric, unimodal, bell curve is ubiquitous
Frequency Distributions
 Displaying Data Frequency Distributions After collecting data, the first task for a researcher is to organize and summarize the data so that it is possible to get a general overview of the results. Remember,
Displaying Data Frequency Distributions After collecting data, the first task for a researcher is to organize and summarize the data so that it is possible to get a general overview of the results. Remember,
Chapter 2: The Normal Distributions
 Chapter 2: The Normal Distributions Measures of Relative Standing & Density Curves Z-scores (Measures of Relative Standing) Suppose there is one spot left in the University of Michigan class of 2014 and
Chapter 2: The Normal Distributions Measures of Relative Standing & Density Curves Z-scores (Measures of Relative Standing) Suppose there is one spot left in the University of Michigan class of 2014 and
Key: 5 9 represents a team with 59 wins. (c) The Kansas City Royals and Cleveland Indians, who both won 65 games.
 AP statistics Chapter 2 Notes Name Modeling Distributions of Data Per Date 2.1A Distribution of a variable is the a variable takes and it takes that value. When working with quantitative data we can calculate
AP statistics Chapter 2 Notes Name Modeling Distributions of Data Per Date 2.1A Distribution of a variable is the a variable takes and it takes that value. When working with quantitative data we can calculate
Chapter 6. THE NORMAL DISTRIBUTION
 Chapter 6. THE NORMAL DISTRIBUTION Introducing Normally Distributed Variables The distributions of some variables like thickness of the eggshell, serum cholesterol concentration in blood, white blood cells
Chapter 6. THE NORMAL DISTRIBUTION Introducing Normally Distributed Variables The distributions of some variables like thickness of the eggshell, serum cholesterol concentration in blood, white blood cells
Chapter 3 Analyzing Normal Quantitative Data
 Chapter 3 Analyzing Normal Quantitative Data Introduction: In chapters 1 and 2, we focused on analyzing categorical data and exploring relationships between categorical data sets. We will now be doing
Chapter 3 Analyzing Normal Quantitative Data Introduction: In chapters 1 and 2, we focused on analyzing categorical data and exploring relationships between categorical data sets. We will now be doing
The first few questions on this worksheet will deal with measures of central tendency. These data types tell us where the center of the data set lies.
 Instructions: You are given the following data below these instructions. Your client (Courtney) wants you to statistically analyze the data to help her reach conclusions about how well she is teaching.
Instructions: You are given the following data below these instructions. Your client (Courtney) wants you to statistically analyze the data to help her reach conclusions about how well she is teaching.
Chapter 6 Normal Probability Distributions
 Chapter 6 Normal Probability Distributions 6-1 Review and Preview 6-2 The Standard Normal Distribution 6-3 Applications of Normal Distributions 6-4 Sampling Distributions and Estimators 6-5 The Central
Chapter 6 Normal Probability Distributions 6-1 Review and Preview 6-2 The Standard Normal Distribution 6-3 Applications of Normal Distributions 6-4 Sampling Distributions and Estimators 6-5 The Central
Math 120 Introduction to Statistics Mr. Toner s Lecture Notes 3.1 Measures of Central Tendency
 Math 1 Introduction to Statistics Mr. Toner s Lecture Notes 3.1 Measures of Central Tendency lowest value + highest value midrange The word average: is very ambiguous and can actually refer to the mean,
Math 1 Introduction to Statistics Mr. Toner s Lecture Notes 3.1 Measures of Central Tendency lowest value + highest value midrange The word average: is very ambiguous and can actually refer to the mean,
The Normal Distribution
 The Normal Distribution Lecture 20 Section 6.3.1 Robb T. Koether Hampden-Sydney College Wed, Sep 28, 2011 Robb T. Koether (Hampden-Sydney College) The Normal Distribution Wed, Sep 28, 2011 1 / 41 Outline
The Normal Distribution Lecture 20 Section 6.3.1 Robb T. Koether Hampden-Sydney College Wed, Sep 28, 2011 Robb T. Koether (Hampden-Sydney College) The Normal Distribution Wed, Sep 28, 2011 1 / 41 Outline
Chapter 6: DESCRIPTIVE STATISTICS
 Chapter 6: DESCRIPTIVE STATISTICS Random Sampling Numerical Summaries Stem-n-Leaf plots Histograms, and Box plots Time Sequence Plots Normal Probability Plots Sections 6-1 to 6-5, and 6-7 Random Sampling
Chapter 6: DESCRIPTIVE STATISTICS Random Sampling Numerical Summaries Stem-n-Leaf plots Histograms, and Box plots Time Sequence Plots Normal Probability Plots Sections 6-1 to 6-5, and 6-7 Random Sampling
Name: Date: Period: Chapter 2. Section 1: Describing Location in a Distribution
 Name: Date: Period: Chapter 2 Section 1: Describing Location in a Distribution Suppose you earned an 86 on a statistics quiz. The question is: should you be satisfied with this score? What if it is the
Name: Date: Period: Chapter 2 Section 1: Describing Location in a Distribution Suppose you earned an 86 on a statistics quiz. The question is: should you be satisfied with this score? What if it is the
UNIT 1A EXPLORING UNIVARIATE DATA
 A.P. STATISTICS E. Villarreal Lincoln HS Math Department UNIT 1A EXPLORING UNIVARIATE DATA LESSON 1: TYPES OF DATA Here is a list of important terms that we must understand as we begin our study of statistics
A.P. STATISTICS E. Villarreal Lincoln HS Math Department UNIT 1A EXPLORING UNIVARIATE DATA LESSON 1: TYPES OF DATA Here is a list of important terms that we must understand as we begin our study of statistics
Averages and Variation
 Averages and Variation 3 Copyright Cengage Learning. All rights reserved. 3.1-1 Section 3.1 Measures of Central Tendency: Mode, Median, and Mean Copyright Cengage Learning. All rights reserved. 3.1-2 Focus
Averages and Variation 3 Copyright Cengage Learning. All rights reserved. 3.1-1 Section 3.1 Measures of Central Tendency: Mode, Median, and Mean Copyright Cengage Learning. All rights reserved. 3.1-2 Focus
CHAPTER 2 Modeling Distributions of Data
 CHAPTER 2 Modeling Distributions of Data 2.2 Density Curves and Normal Distributions The Practice of Statistics, 5th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers Density Curves
CHAPTER 2 Modeling Distributions of Data 2.2 Density Curves and Normal Distributions The Practice of Statistics, 5th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers Density Curves
Introduction to the Practice of Statistics Fifth Edition Moore, McCabe
 Introduction to the Practice of Statistics Fifth Edition Moore, McCabe Section 1.3 Homework Answers Assignment 5 1.80 If you ask a computer to generate "random numbers between 0 and 1, you uniform will
Introduction to the Practice of Statistics Fifth Edition Moore, McCabe Section 1.3 Homework Answers Assignment 5 1.80 If you ask a computer to generate "random numbers between 0 and 1, you uniform will
Chapter 2: Modeling Distributions of Data
 Chapter 2: Modeling Distributions of Data Section 2.2 The Practice of Statistics, 4 th edition - For AP* STARNES, YATES, MOORE Chapter 2 Modeling Distributions of Data 2.1 Describing Location in a Distribution
Chapter 2: Modeling Distributions of Data Section 2.2 The Practice of Statistics, 4 th edition - For AP* STARNES, YATES, MOORE Chapter 2 Modeling Distributions of Data 2.1 Describing Location in a Distribution
CHAPTER 2 DESCRIPTIVE STATISTICS
 CHAPTER 2 DESCRIPTIVE STATISTICS 1. Stem-and-Leaf Graphs, Line Graphs, and Bar Graphs The distribution of data is how the data is spread or distributed over the range of the data values. This is one of
CHAPTER 2 DESCRIPTIVE STATISTICS 1. Stem-and-Leaf Graphs, Line Graphs, and Bar Graphs The distribution of data is how the data is spread or distributed over the range of the data values. This is one of
10.4 Measures of Central Tendency and Variation
 10.4 Measures of Central Tendency and Variation Mode-->The number that occurs most frequently; there can be more than one mode ; if each number appears equally often, then there is no mode at all. (mode
10.4 Measures of Central Tendency and Variation Mode-->The number that occurs most frequently; there can be more than one mode ; if each number appears equally often, then there is no mode at all. (mode
10.4 Measures of Central Tendency and Variation
 10.4 Measures of Central Tendency and Variation Mode-->The number that occurs most frequently; there can be more than one mode ; if each number appears equally often, then there is no mode at all. (mode
10.4 Measures of Central Tendency and Variation Mode-->The number that occurs most frequently; there can be more than one mode ; if each number appears equally often, then there is no mode at all. (mode
The Normal Distribution & z-scores
 & z-scores Distributions: Who needs them? Why are we interested in distributions? Important link between distributions and probabilities of events If we know the distribution of a set of events, then we
& z-scores Distributions: Who needs them? Why are we interested in distributions? Important link between distributions and probabilities of events If we know the distribution of a set of events, then we
23.2 Normal Distributions
 1_ Locker LESSON 23.2 Normal Distributions Common Core Math Standards The student is expected to: S-ID.4 Use the mean and standard deviation of a data set to fit it to a normal distribution and to estimate
1_ Locker LESSON 23.2 Normal Distributions Common Core Math Standards The student is expected to: S-ID.4 Use the mean and standard deviation of a data set to fit it to a normal distribution and to estimate
Vocabulary. 5-number summary Rule. Area principle. Bar chart. Boxplot. Categorical data condition. Categorical variable.
 5-number summary 68-95-99.7 Rule Area principle Bar chart Bimodal Boxplot Case Categorical data Categorical variable Center Changing center and spread Conditional distribution Context Contingency table
5-number summary 68-95-99.7 Rule Area principle Bar chart Bimodal Boxplot Case Categorical data Categorical variable Center Changing center and spread Conditional distribution Context Contingency table
2.1 Objectives. Math Chapter 2. Chapter 2. Variable. Categorical Variable EXPLORING DATA WITH GRAPHS AND NUMERICAL SUMMARIES
 EXPLORING DATA WITH GRAPHS AND NUMERICAL SUMMARIES Chapter 2 2.1 Objectives 2.1 What Are the Types of Data? www.managementscientist.org 1. Know the definitions of a. Variable b. Categorical versus quantitative
EXPLORING DATA WITH GRAPHS AND NUMERICAL SUMMARIES Chapter 2 2.1 Objectives 2.1 What Are the Types of Data? www.managementscientist.org 1. Know the definitions of a. Variable b. Categorical versus quantitative
CHAPTER 2 Modeling Distributions of Data
 CHAPTER 2 Modeling Distributions of Data 2.2 Density Curves and Normal Distributions The Practice of Statistics, 5th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers HW 34. Sketch
CHAPTER 2 Modeling Distributions of Data 2.2 Density Curves and Normal Distributions The Practice of Statistics, 5th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers HW 34. Sketch
Lecture 6: Chapter 6 Summary
 1 Lecture 6: Chapter 6 Summary Z-score: Is the distance of each data value from the mean in standard deviation Standardizes data values Standardization changes the mean and the standard deviation: o Z
1 Lecture 6: Chapter 6 Summary Z-score: Is the distance of each data value from the mean in standard deviation Standardizes data values Standardization changes the mean and the standard deviation: o Z
Section 2.2 Normal Distributions. Normal Distributions
 Section 2.2 Normal Distributions Normal Distributions One particularly important class of density curves are the Normal curves, which describe Normal distributions. All Normal curves are symmetric, single-peaked,
Section 2.2 Normal Distributions Normal Distributions One particularly important class of density curves are the Normal curves, which describe Normal distributions. All Normal curves are symmetric, single-peaked,
Math 14 Lecture Notes Ch. 6.1
 6.1 Normal Distribution What is normal? a 10-year old boy that is 4' tall? 5' tall? 6' tall? a 25-year old woman with a shoe size of 5? 7? 9? an adult alligator that weighs 200 pounds? 500 pounds? 800
6.1 Normal Distribution What is normal? a 10-year old boy that is 4' tall? 5' tall? 6' tall? a 25-year old woman with a shoe size of 5? 7? 9? an adult alligator that weighs 200 pounds? 500 pounds? 800
Chapter 2 Describing, Exploring, and Comparing Data
 Slide 1 Chapter 2 Describing, Exploring, and Comparing Data Slide 2 2-1 Overview 2-2 Frequency Distributions 2-3 Visualizing Data 2-4 Measures of Center 2-5 Measures of Variation 2-6 Measures of Relative
Slide 1 Chapter 2 Describing, Exploring, and Comparing Data Slide 2 2-1 Overview 2-2 Frequency Distributions 2-3 Visualizing Data 2-4 Measures of Center 2-5 Measures of Variation 2-6 Measures of Relative
Chapter 2: The Normal Distribution
 Chapter 2: The Normal Distribution 2.1 Density Curves and the Normal Distributions 2.2 Standard Normal Calculations 1 2 Histogram for Strength of Yarn Bobbins 15.60 16.10 16.60 17.10 17.60 18.10 18.60
Chapter 2: The Normal Distribution 2.1 Density Curves and the Normal Distributions 2.2 Standard Normal Calculations 1 2 Histogram for Strength of Yarn Bobbins 15.60 16.10 16.60 17.10 17.60 18.10 18.60
Distributions of Continuous Data
 C H A P T ER Distributions of Continuous Data New cars and trucks sold in the United States average about 28 highway miles per gallon (mpg) in 2010, up from about 24 mpg in 2004. Some of the improvement
C H A P T ER Distributions of Continuous Data New cars and trucks sold in the United States average about 28 highway miles per gallon (mpg) in 2010, up from about 24 mpg in 2004. Some of the improvement
Measures of Central Tendency. A measure of central tendency is a value used to represent the typical or average value in a data set.
 Measures of Central Tendency A measure of central tendency is a value used to represent the typical or average value in a data set. The Mean the sum of all data values divided by the number of values in
Measures of Central Tendency A measure of central tendency is a value used to represent the typical or average value in a data set. The Mean the sum of all data values divided by the number of values in
Chapter 6. The Normal Distribution. McGraw-Hill, Bluman, 7 th ed., Chapter 6 1
 Chapter 6 The Normal Distribution McGraw-Hill, Bluman, 7 th ed., Chapter 6 1 Bluman, Chapter 6 2 Chapter 6 Overview Introduction 6-1 Normal Distributions 6-2 Applications of the Normal Distribution 6-3
Chapter 6 The Normal Distribution McGraw-Hill, Bluman, 7 th ed., Chapter 6 1 Bluman, Chapter 6 2 Chapter 6 Overview Introduction 6-1 Normal Distributions 6-2 Applications of the Normal Distribution 6-3
STP 226 ELEMENTARY STATISTICS NOTES PART 2 - DESCRIPTIVE STATISTICS CHAPTER 3 DESCRIPTIVE MEASURES
 STP 6 ELEMENTARY STATISTICS NOTES PART - DESCRIPTIVE STATISTICS CHAPTER 3 DESCRIPTIVE MEASURES Chapter covered organizing data into tables, and summarizing data with graphical displays. We will now use
STP 6 ELEMENTARY STATISTICS NOTES PART - DESCRIPTIVE STATISTICS CHAPTER 3 DESCRIPTIVE MEASURES Chapter covered organizing data into tables, and summarizing data with graphical displays. We will now use
AND NUMERICAL SUMMARIES. Chapter 2
 EXPLORING DATA WITH GRAPHS AND NUMERICAL SUMMARIES Chapter 2 2.1 What Are the Types of Data? 2.1 Objectives www.managementscientist.org 1. Know the definitions of a. Variable b. Categorical versus quantitative
EXPLORING DATA WITH GRAPHS AND NUMERICAL SUMMARIES Chapter 2 2.1 What Are the Types of Data? 2.1 Objectives www.managementscientist.org 1. Know the definitions of a. Variable b. Categorical versus quantitative
The Normal Distribution. John McGready, PhD Johns Hopkins University
 The Normal Distribution John McGready, PhD Johns Hopkins University General Properties of The Normal Distribution The material in this video is subject to the copyright of the owners of the material and
The Normal Distribution John McGready, PhD Johns Hopkins University General Properties of The Normal Distribution The material in this video is subject to the copyright of the owners of the material and
Measures of Central Tendency
 Page of 6 Measures of Central Tendency A measure of central tendency is a value used to represent the typical or average value in a data set. The Mean The sum of all data values divided by the number of
Page of 6 Measures of Central Tendency A measure of central tendency is a value used to represent the typical or average value in a data set. The Mean The sum of all data values divided by the number of
MAT 110 WORKSHOP. Updated Fall 2018
 MAT 110 WORKSHOP Updated Fall 2018 UNIT 3: STATISTICS Introduction Choosing a Sample Simple Random Sample: a set of individuals from the population chosen in a way that every individual has an equal chance
MAT 110 WORKSHOP Updated Fall 2018 UNIT 3: STATISTICS Introduction Choosing a Sample Simple Random Sample: a set of individuals from the population chosen in a way that every individual has an equal chance
Normal Distribution. 6.4 Applications of Normal Distribution
 Normal Distribution 6.4 Applications of Normal Distribution 1 /20 Homework Read Sec 6-4. Discussion question p316 Do p316 probs 1-10, 16-22, 31, 32, 34-37, 39 2 /20 3 /20 Objective Find the probabilities
Normal Distribution 6.4 Applications of Normal Distribution 1 /20 Homework Read Sec 6-4. Discussion question p316 Do p316 probs 1-10, 16-22, 31, 32, 34-37, 39 2 /20 3 /20 Objective Find the probabilities
Learning Objectives. Continuous Random Variables & The Normal Probability Distribution. Continuous Random Variable
 Learning Objectives Continuous Random Variables & The Normal Probability Distribution 1. Understand characteristics about continuous random variables and probability distributions 2. Understand the uniform
Learning Objectives Continuous Random Variables & The Normal Probability Distribution 1. Understand characteristics about continuous random variables and probability distributions 2. Understand the uniform
Chapter 5: The normal model
 Chapter 5: The normal model Objective (1) Learn how rescaling a distribution affects its summary statistics. (2) Understand the concept of normal model. (3) Learn how to analyze distributions using the
Chapter 5: The normal model Objective (1) Learn how rescaling a distribution affects its summary statistics. (2) Understand the concept of normal model. (3) Learn how to analyze distributions using the
STA Rev. F Learning Objectives. Learning Objectives (Cont.) Module 3 Descriptive Measures
 STA 2023 Module 3 Descriptive Measures Learning Objectives Upon completing this module, you should be able to: 1. Explain the purpose of a measure of center. 2. Obtain and interpret the mean, median, and
STA 2023 Module 3 Descriptive Measures Learning Objectives Upon completing this module, you should be able to: 1. Explain the purpose of a measure of center. 2. Obtain and interpret the mean, median, and
Lecture Slides. Elementary Statistics Twelfth Edition. by Mario F. Triola. and the Triola Statistics Series. Section 2.1- #
 Lecture Slides Elementary Statistics Twelfth Edition and the Triola Statistics Series by Mario F. Triola Chapter 2 Summarizing and Graphing Data 2-1 Review and Preview 2-2 Frequency Distributions 2-3 Histograms
Lecture Slides Elementary Statistics Twelfth Edition and the Triola Statistics Series by Mario F. Triola Chapter 2 Summarizing and Graphing Data 2-1 Review and Preview 2-2 Frequency Distributions 2-3 Histograms
MATH 1070 Introductory Statistics Lecture notes Descriptive Statistics and Graphical Representation
 MATH 1070 Introductory Statistics Lecture notes Descriptive Statistics and Graphical Representation Objectives: 1. Learn the meaning of descriptive versus inferential statistics 2. Identify bar graphs,
MATH 1070 Introductory Statistics Lecture notes Descriptive Statistics and Graphical Representation Objectives: 1. Learn the meaning of descriptive versus inferential statistics 2. Identify bar graphs,
No. of blue jelly beans No. of bags
 Math 167 Ch5 Review 1 (c) Janice Epstein CHAPTER 5 EXPLORING DATA DISTRIBUTIONS A sample of jelly bean bags is chosen and the number of blue jelly beans in each bag is counted. The results are shown in
Math 167 Ch5 Review 1 (c) Janice Epstein CHAPTER 5 EXPLORING DATA DISTRIBUTIONS A sample of jelly bean bags is chosen and the number of blue jelly beans in each bag is counted. The results are shown in
Week 2: Frequency distributions
 Types of data Health Sciences M.Sc. Programme Applied Biostatistics Week 2: distributions Data can be summarised to help to reveal information they contain. We do this by calculating numbers from the data
Types of data Health Sciences M.Sc. Programme Applied Biostatistics Week 2: distributions Data can be summarised to help to reveal information they contain. We do this by calculating numbers from the data
CHAPTER 2 Modeling Distributions of Data
 CHAPTER 2 Modeling Distributions of Data 2.2 Density Curves and Normal Distributions The Practice of Statistics, 5th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers Density Curves
CHAPTER 2 Modeling Distributions of Data 2.2 Density Curves and Normal Distributions The Practice of Statistics, 5th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers Density Curves
The Normal Distribution & z-scores
 & z-scores Distributions: Who needs them? Why are we interested in distributions? Important link between distributions and probabilities of events If we know the distribution of a set of events, then we
& z-scores Distributions: Who needs them? Why are we interested in distributions? Important link between distributions and probabilities of events If we know the distribution of a set of events, then we
Chapter2 Description of samples and populations. 2.1 Introduction.
 Chapter2 Description of samples and populations. 2.1 Introduction. Statistics=science of analyzing data. Information collected (data) is gathered in terms of variables (characteristics of a subject that
Chapter2 Description of samples and populations. 2.1 Introduction. Statistics=science of analyzing data. Information collected (data) is gathered in terms of variables (characteristics of a subject that
CHAPTER 2: Describing Location in a Distribution
 CHAPTER 2: Describing Location in a Distribution 2.1 Goals: 1. Compute and use z-scores given the mean and sd 2. Compute and use the p th percentile of an observation 3. Intro to density curves 4. More
CHAPTER 2: Describing Location in a Distribution 2.1 Goals: 1. Compute and use z-scores given the mean and sd 2. Compute and use the p th percentile of an observation 3. Intro to density curves 4. More
Ch6: The Normal Distribution
 Ch6: The Normal Distribution Introduction Review: A continuous random variable can assume any value between two endpoints. Many continuous random variables have an approximately normal distribution, which
Ch6: The Normal Distribution Introduction Review: A continuous random variable can assume any value between two endpoints. Many continuous random variables have an approximately normal distribution, which
3 Graphical Displays of Data
 3 Graphical Displays of Data Reading: SW Chapter 2, Sections 1-6 Summarizing and Displaying Qualitative Data The data below are from a study of thyroid cancer, using NMTR data. The investigators looked
3 Graphical Displays of Data Reading: SW Chapter 2, Sections 1-6 Summarizing and Displaying Qualitative Data The data below are from a study of thyroid cancer, using NMTR data. The investigators looked
MAT 102 Introduction to Statistics Chapter 6. Chapter 6 Continuous Probability Distributions and the Normal Distribution
 MAT 102 Introduction to Statistics Chapter 6 Chapter 6 Continuous Probability Distributions and the Normal Distribution 6.2 Continuous Probability Distributions Characteristics of a Continuous Probability
MAT 102 Introduction to Statistics Chapter 6 Chapter 6 Continuous Probability Distributions and the Normal Distribution 6.2 Continuous Probability Distributions Characteristics of a Continuous Probability
Learner Expectations UNIT 1: GRAPICAL AND NUMERIC REPRESENTATIONS OF DATA. Sept. Fathom Lab: Distributions and Best Methods of Display
 CURRICULUM MAP TEMPLATE Priority Standards = Approximately 70% Supporting Standards = Approximately 20% Additional Standards = Approximately 10% HONORS PROBABILITY AND STATISTICS Essential Questions &
CURRICULUM MAP TEMPLATE Priority Standards = Approximately 70% Supporting Standards = Approximately 20% Additional Standards = Approximately 10% HONORS PROBABILITY AND STATISTICS Essential Questions &
Chapter 6 The Standard Deviation as Ruler and the Normal Model
 ST 305 Chapter 6 Reiland The Standard Deviation as Ruler and the Normal Model Chapter Objectives: At the end of this chapter you should be able to: 1) describe how adding or subtracting the same value
ST 305 Chapter 6 Reiland The Standard Deviation as Ruler and the Normal Model Chapter Objectives: At the end of this chapter you should be able to: 1) describe how adding or subtracting the same value
Measures of Dispersion
 Measures of Dispersion 6-3 I Will... Find measures of dispersion of sets of data. Find standard deviation and analyze normal distribution. Day 1: Dispersion Vocabulary Measures of Variation (Dispersion
Measures of Dispersion 6-3 I Will... Find measures of dispersion of sets of data. Find standard deviation and analyze normal distribution. Day 1: Dispersion Vocabulary Measures of Variation (Dispersion
Student Learning Objectives
 Student Learning Objectives A. Understand that the overall shape of a distribution of a large number of observations can be summarized by a smooth curve called a density curve. B. Know that an area under
Student Learning Objectives A. Understand that the overall shape of a distribution of a large number of observations can be summarized by a smooth curve called a density curve. B. Know that an area under
Section 2.2 Normal Distributions
 Section 2.2 Mrs. Daniel AP Statistics We abbreviate the Normal distribution with mean µ and standard deviation σ as N(µ,σ). Any particular Normal distribution is completely specified by two numbers: its
Section 2.2 Mrs. Daniel AP Statistics We abbreviate the Normal distribution with mean µ and standard deviation σ as N(µ,σ). Any particular Normal distribution is completely specified by two numbers: its
Normal Data ID1050 Quantitative & Qualitative Reasoning
 Normal Data ID1050 Quantitative & Qualitative Reasoning Histogram for Different Sample Sizes For a small sample, the choice of class (group) size dramatically affects how the histogram appears. Say we
Normal Data ID1050 Quantitative & Qualitative Reasoning Histogram for Different Sample Sizes For a small sample, the choice of class (group) size dramatically affects how the histogram appears. Say we
CHAPTER 2: DESCRIPTIVE STATISTICS Lecture Notes for Introductory Statistics 1. Daphne Skipper, Augusta University (2016)
 CHAPTER 2: DESCRIPTIVE STATISTICS Lecture Notes for Introductory Statistics 1 Daphne Skipper, Augusta University (2016) 1. Stem-and-Leaf Graphs, Line Graphs, and Bar Graphs The distribution of data is
CHAPTER 2: DESCRIPTIVE STATISTICS Lecture Notes for Introductory Statistics 1 Daphne Skipper, Augusta University (2016) 1. Stem-and-Leaf Graphs, Line Graphs, and Bar Graphs The distribution of data is
The Normal Distribution & z-scores
 & z-scores Distributions: Who needs them? Why are we interested in distributions? Important link between distributions and probabilities of events If we know the distribution of a set of events, then we
& z-scores Distributions: Who needs them? Why are we interested in distributions? Important link between distributions and probabilities of events If we know the distribution of a set of events, then we
AP Statistics Summer Assignment:
 AP Statistics Summer Assignment: Read the following and use the information to help answer your summer assignment questions. You will be responsible for knowing all of the information contained in this
AP Statistics Summer Assignment: Read the following and use the information to help answer your summer assignment questions. You will be responsible for knowing all of the information contained in this
6-1 THE STANDARD NORMAL DISTRIBUTION
 6-1 THE STANDARD NORMAL DISTRIBUTION The major focus of this chapter is the concept of a normal probability distribution, but we begin with a uniform distribution so that we can see the following two very
6-1 THE STANDARD NORMAL DISTRIBUTION The major focus of this chapter is the concept of a normal probability distribution, but we begin with a uniform distribution so that we can see the following two very
Lecture Series on Statistics -HSTC. Frequency Graphs " Dr. Bijaya Bhusan Nanda, Ph. D. (Stat.)
 Lecture Series on Statistics -HSTC Frequency Graphs " By Dr. Bijaya Bhusan Nanda, Ph. D. (Stat.) CONTENT Histogram Frequency polygon Smoothed frequency curve Cumulative frequency curve or ogives Learning
Lecture Series on Statistics -HSTC Frequency Graphs " By Dr. Bijaya Bhusan Nanda, Ph. D. (Stat.) CONTENT Histogram Frequency polygon Smoothed frequency curve Cumulative frequency curve or ogives Learning
ECLT 5810 Data Preprocessing. Prof. Wai Lam
 ECLT 5810 Data Preprocessing Prof. Wai Lam Why Data Preprocessing? Data in the real world is imperfect incomplete: lacking attribute values, lacking certain attributes of interest, or containing only aggregate
ECLT 5810 Data Preprocessing Prof. Wai Lam Why Data Preprocessing? Data in the real world is imperfect incomplete: lacking attribute values, lacking certain attributes of interest, or containing only aggregate
Continuous Improvement Toolkit. Normal Distribution. Continuous Improvement Toolkit.
 Continuous Improvement Toolkit Normal Distribution The Continuous Improvement Map Managing Risk FMEA Understanding Performance** Check Sheets Data Collection PDPC RAID Log* Risk Analysis* Benchmarking***
Continuous Improvement Toolkit Normal Distribution The Continuous Improvement Map Managing Risk FMEA Understanding Performance** Check Sheets Data Collection PDPC RAID Log* Risk Analysis* Benchmarking***
The standard deviation 1 n
 The standard deviation 1 SD = (xj x) n 2 The SD gives a measure of how the data are clustered around the mean. If the SD is larger, then the data are more spread out we are more likely to find data that
The standard deviation 1 SD = (xj x) n 2 The SD gives a measure of how the data are clustered around the mean. If the SD is larger, then the data are more spread out we are more likely to find data that
How individual data points are positioned within a data set.
 Section 3.4 Measures of Position Percentiles How individual data points are positioned within a data set. P k is the value such that k% of a data set is less than or equal to P k. For example if we said
Section 3.4 Measures of Position Percentiles How individual data points are positioned within a data set. P k is the value such that k% of a data set is less than or equal to P k. For example if we said
Univariate Statistics Summary
 Further Maths Univariate Statistics Summary Types of Data Data can be classified as categorical or numerical. Categorical data are observations or records that are arranged according to category. For example:
Further Maths Univariate Statistics Summary Types of Data Data can be classified as categorical or numerical. Categorical data are observations or records that are arranged according to category. For example:
4.3 The Normal Distribution
 4.3 The Normal Distribution Objectives. Definition of normal distribution. Standard normal distribution. Specialties of the graph of the standard normal distribution. Percentiles of the standard normal
4.3 The Normal Distribution Objectives. Definition of normal distribution. Standard normal distribution. Specialties of the graph of the standard normal distribution. Percentiles of the standard normal
CHAPTER 2: SAMPLING AND DATA
 CHAPTER 2: SAMPLING AND DATA This presentation is based on material and graphs from Open Stax and is copyrighted by Open Stax and Georgia Highlands College. OUTLINE 2.1 Stem-and-Leaf Graphs (Stemplots),
CHAPTER 2: SAMPLING AND DATA This presentation is based on material and graphs from Open Stax and is copyrighted by Open Stax and Georgia Highlands College. OUTLINE 2.1 Stem-and-Leaf Graphs (Stemplots),
CHAPTER 6. The Normal Probability Distribution
 The Normal Probability Distribution CHAPTER 6 The normal probability distribution is the most widely used distribution in statistics as many statistical procedures are built around it. The central limit
The Normal Probability Distribution CHAPTER 6 The normal probability distribution is the most widely used distribution in statistics as many statistical procedures are built around it. The central limit
SCHOOL OF BUSINESS, ECONOMICS AND MANAGEMENT BBA240 STATISTICS/ QUANTITATIVE METHODS FOR BUSINESS AND ECONOMICS
 SCHOOL OF BUSINESS, ECONOMICS AND MANAGEMENT BBA240 STATISTICS/ QUANTITATIVE METHODS FOR BUSINESS AND ECONOMICS Unit Two Moses Mwale e-mail: moses.mwale@ictar.ac.zm ii Contents Contents UNIT 2: Numerical
SCHOOL OF BUSINESS, ECONOMICS AND MANAGEMENT BBA240 STATISTICS/ QUANTITATIVE METHODS FOR BUSINESS AND ECONOMICS Unit Two Moses Mwale e-mail: moses.mwale@ictar.ac.zm ii Contents Contents UNIT 2: Numerical
Unit 8: Normal Calculations
 Unit 8: Normal Calculations Prerequisites This unit requires familiarity with basic facts about normal distributions, which are covered in Unit 7, Normal Curves. In addition, students need some background
Unit 8: Normal Calculations Prerequisites This unit requires familiarity with basic facts about normal distributions, which are covered in Unit 7, Normal Curves. In addition, students need some background
AP Statistics. Study Guide
 Measuring Relative Standing Standardized Values and z-scores AP Statistics Percentiles Rank the data lowest to highest. Counting up from the lowest value to the select data point we discover the percentile
Measuring Relative Standing Standardized Values and z-scores AP Statistics Percentiles Rank the data lowest to highest. Counting up from the lowest value to the select data point we discover the percentile
1 Overview of Statistics; Essential Vocabulary
 1 Overview of Statistics; Essential Vocabulary Statistics: the science of collecting, organizing, analyzing, and interpreting data in order to make decisions Population and sample Population: the entire
1 Overview of Statistics; Essential Vocabulary Statistics: the science of collecting, organizing, analyzing, and interpreting data in order to make decisions Population and sample Population: the entire
Measures of Position
 Measures of Position In this section, we will learn to use fractiles. Fractiles are numbers that partition, or divide, an ordered data set into equal parts (each part has the same number of data entries).
Measures of Position In this section, we will learn to use fractiles. Fractiles are numbers that partition, or divide, an ordered data set into equal parts (each part has the same number of data entries).
CHAPTER 1. Introduction. Statistics: Statistics is the science of collecting, organizing, analyzing, presenting and interpreting data.
 1 CHAPTER 1 Introduction Statistics: Statistics is the science of collecting, organizing, analyzing, presenting and interpreting data. Variable: Any characteristic of a person or thing that can be expressed
1 CHAPTER 1 Introduction Statistics: Statistics is the science of collecting, organizing, analyzing, presenting and interpreting data. Variable: Any characteristic of a person or thing that can be expressed
3 Graphical Displays of Data
 3 Graphical Displays of Data Reading: SW Chapter 2, Sections 1-6 Summarizing and Displaying Qualitative Data The data below are from a study of thyroid cancer, using NMTR data. The investigators looked
3 Graphical Displays of Data Reading: SW Chapter 2, Sections 1-6 Summarizing and Displaying Qualitative Data The data below are from a study of thyroid cancer, using NMTR data. The investigators looked
The basic arrangement of numeric data is called an ARRAY. Array is the derived data from fundamental data Example :- To store marks of 50 student
 Organizing data Learning Outcome 1. make an array 2. divide the array into class intervals 3. describe the characteristics of a table 4. construct a frequency distribution table 5. constructing a composite
Organizing data Learning Outcome 1. make an array 2. divide the array into class intervals 3. describe the characteristics of a table 4. construct a frequency distribution table 5. constructing a composite
Normal Curves and Sampling Distributions
 Normal Curves and Sampling Distributions 6 Copyright Cengage Learning. All rights reserved. Section 6.2 Standard Units and Areas Under the Standard Normal Distribution Copyright Cengage Learning. All rights
Normal Curves and Sampling Distributions 6 Copyright Cengage Learning. All rights reserved. Section 6.2 Standard Units and Areas Under the Standard Normal Distribution Copyright Cengage Learning. All rights
8: Statistics. Populations and Samples. Histograms and Frequency Polygons. Page 1 of 10
 8: Statistics Statistics: Method of collecting, organizing, analyzing, and interpreting data, as well as drawing conclusions based on the data. Methodology is divided into two main areas. Descriptive Statistics:
8: Statistics Statistics: Method of collecting, organizing, analyzing, and interpreting data, as well as drawing conclusions based on the data. Methodology is divided into two main areas. Descriptive Statistics:
The main issue is that the mean and standard deviations are not accurate and should not be used in the analysis. Then what statistics should we use?
 Chapter 4 Analyzing Skewed Quantitative Data Introduction: In chapter 3, we focused on analyzing bell shaped (normal) data, but many data sets are not bell shaped. How do we analyze quantitative data when
Chapter 4 Analyzing Skewed Quantitative Data Introduction: In chapter 3, we focused on analyzing bell shaped (normal) data, but many data sets are not bell shaped. How do we analyze quantitative data when
Chapter 3 - Displaying and Summarizing Quantitative Data
 Chapter 3 - Displaying and Summarizing Quantitative Data 3.1 Graphs for Quantitative Data (LABEL GRAPHS) August 25, 2014 Histogram (p. 44) - Graph that uses bars to represent different frequencies or relative
Chapter 3 - Displaying and Summarizing Quantitative Data 3.1 Graphs for Quantitative Data (LABEL GRAPHS) August 25, 2014 Histogram (p. 44) - Graph that uses bars to represent different frequencies or relative
MAT 142 College Mathematics. Module ST. Statistics. Terri Miller revised July 14, 2015
 MAT 142 College Mathematics Statistics Module ST Terri Miller revised July 14, 2015 2 Statistics Data Organization and Visualization Basic Terms. A population is the set of all objects under study, a sample
MAT 142 College Mathematics Statistics Module ST Terri Miller revised July 14, 2015 2 Statistics Data Organization and Visualization Basic Terms. A population is the set of all objects under study, a sample
