Chapter 4 Arithmetic Functions
|
|
|
- Mabel Horton
- 5 years ago
- Views:
Transcription
1 Logic and Computer Design Fundamentals Chapter 4 Arithmetic Functions Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active in View Show mode)
2 Overview Iterative combinational circuits Binary adders Half and full adders Ripple carry adders Binary subtraction Signed binary numbers Signed binary addition and subtraction Binary adder- subtractor Overflow Binary multiplication Other arithmetic functions Design by contraction Chapter 4 2
3 Iterative Combinational Circuits Arithmetic functions Operate on binary vectors Use the same subfunction in each bit position Can design functional block for subfunction and repeat to obtain functional block for overall function Cell - subfunction block Iterative array - a array of interconnected cells An iterative array can be in a single dimension (1D) or multiple dimensions Chapter 4 3
4 Block Diagram of a 1D Iterative Array Example: n = 32 Number of inputs =? Truth table rows =? Equations with up to? input variables Equations with huge number of terms Design impractical! Iterative array takes advantage of the regularity to make design feasible Chapter 4 4
5 Functional Blocks: Addition Binary addition used frequently Addition Development: Half-Adder (HA), a 2-input bit-wise addition functional block, Full-Adder (FA), a 3-input bit-wise addition functional block, Ripple Carry Adder, an iterative array to perform binary addition. Chapter 4 5
6 Functional Block: Half-Adder A 2-input, 1-bit width binary adder that performs the following computations: X C S A half adder adds two bits to produce a two-bit sum The sum is expressed as a sum bit, S and a carry bit, C The half adder can be specified as a truth table for S and C + Y X Y C S Chapter 4 6
7 Logic Simplification: Half-Adder The K-Map for S, C is given below This is a pretty trivial map! S Y C Y X X S = X Y + X Y = X Y C = X Y Chapter 4 7
8 Five Different Implementations for Half-Adder We can derive following sets of equations for a halfadder: (a) S = X Y + X Y C = X Y (b) S = (X + Y) (X + Y) C = X Y (c) S = ( C+ X Y) C = X Y (d) S = (X + Y) C C (X Y) (e) S = = X Y C = + X Y (a), (b), and (e) are SOP, POS, and XOR implementations for S. In (c), the C function is used as a term in the AND- NOR implementation of S, and in (d), the C function is used in a POS term for S. Chapter 4 8
9 Implementations: Half-Adder The most common half adder implementation is: S = X Y C = X Y X Y S C (e) A NAND only implementation is: S = (X C = ( + Y) C ) ( X Y) X C S Y Chapter 4 9
10 Functional Block: Full-Adder A full adder is similar to a half adder, but includes a carry-in bit from lower stages. Like the half-adder, it computes a sum bit, S and a carry bit, C. For a carry-in (Z) of 0, it is the same as the half-adder: For a carry- in (Z) of 1: Z X Y C S Z X Y C S Chapter 4 10
11 Logic Optimization: Full-Adder Full-Adder Truth Table: Full-Adder K-Map: X Y Z C S S Y C Y X X Z Z Chapter 4 11
12 Equations: Full-Adder From the K-Map, we get: S = X Y Z + X Y Z + C = X Y + X Z + Y Z X Y Z + X Y Z The S function is the three-bit XOR function (Odd Function): S = X Y Z The Carry bit C is 1 if both X and Y are 1 (the sum is 2), or if the sum is 1 and a carry-in (Z) occurs. Chapter 4 12
13 Implementation: Full Adder Full Adder Schematic Chapter 4 13
14 Binary Adders To add multiple operands, we bundle logical signals together into vectors and use functional blocks that operate on the vectors Example: 4-bit ripple carry adder: Adds input vectors A(3:0) and B(3:0) to get a sum vector S(3:0) Note: carry out of cell i becomes carry in of cell i + 1 Description Subscript Name Carry In C i Augend A i Addend B i Sum S i Carry out C i+1 Chapter 4 14
15 4-bit Ripple-Carry Binary Adder A four-bit Ripple Carry Adder made from four 1-bit Full Adders: B 3 A 3 B 2 A 2 B 1 A 1 B 0 A 0 FA C 3 C 2 C 1 FA FA FA C 0 C 4 S 3 S 2 S 1 S 0 C0 is assumed to be zero, or we can use a half adder for A 0 and B 0 Chapter 4 15
16 Binary Subtraction: Unsigned Numbers Unsigned numbers are all positive integers including zero Algorithm: Subtract the subtrahend N from the minuend M; result is n bits If no end borrow occurs, then M N, and the result is a nonnegative number and correct. If an end borrow occurs, the N > M and the difference M - N + 2 n is subtracted from 2 n, and a minus sign is appended to the result. Examples: 0 1 End Borrow (-) 0011 Chapter 4 16
17 Binary Subtraction: Complements Two complements: Diminished Radix Complement of N (r - 1) s complement for radix r 1 s complement for radix 2 Defined as (r n - 1) - N Radix Complement r s complement for radix r 2 s complement in binary Defined as r n - N n is the number of digits in the number. The use of complements is very useful in implementing subtraction in computers. Chapter 4 17
18 Binary 1's Complement For r = 2, N = , n = 8 (8 digits): (r n 1) = = or The 1's complement of is then: Since the 2 n 1 factor consists of all 1's and since 1 0 = 1 and 1 1 = 0, the one's complement is obtained by complementing each individual bit (bitwise NOT). Chapter 4 18
19 Binary 2's Complement For r = 2, N = , n = 8 (8 digits), we have: (r n ) = or The 2's complement of is then: Note the result is the 1's complement plus 1, a fact that can be used in designing hardware Chapter 4 19
20 Alternate 2 s Complement Method Given: an n-bit binary number, beginning at the least significant bit and proceeding upward: Copy all least significant 0 s Copy the first 1 Complement all bits thereafter. 2 s Complement Example: Copy underlined bits: 100 and complement bits to the left: Chapter 4 20
21 Unsigned Subtraction with 2 s Complement For n-digit, unsigned numbers M and N, find M - N in base 2: Add the 2's complement of the subtrahend N to the minuend M: M + (2 n - N) = M - N + 2 n If M N, the sum produces end carry 2 n which is discarded; from above, M - N remains. If M < N, the sum does not produce an end carry and, from above, is equal to 2 n - ( N - M ), the 2's complement of ( N - M ). To obtain the result - (N M), take the 2's complement of the sum and place a - to its left. Chapter 4 21
22 Unsigned 2 s Complement Subtraction Example 1 Find s comp The carry of 1 indicates that no correction of the result is required. Chapter 4 22
23 Unsigned 2 s Complement Subtraction Example 2 Find s comp The carry of 0 indicates that a correction of the result is required. Result = ( ) 2 s comp Chapter 4 23
24 Signed Integers Positive numbers and zero can be represented by unsigned n-digit, radix r numbers. We need a representation for negative numbers. To represent a sign (+ or ) we need exactly one more bit of information (1 binary digit gives 2 1 = 2 elements which is exactly what is needed). Since computers use binary numbers, by convention, the most significant bit is interpreted as a sign bit: s a n 2 a 2 a 1 a 0 where: s = 0 for Positive numbers s = 1 for Negative numbers and a i = 0 or 1 represent the magnitude in some form. Chapter 4 24
25 Signed Integer Representations Signed-Magnitude here the n 1 digits are interpreted as a positive magnitude. Signed-Complement here the digits are interpreted as the rest of the complement of the number. There are two possibilities here: Signed 1's Complement Uses 1's Complement Arithmetic Signed 2's Complement Uses 2's Complement Arithmetic Chapter 4 25
26 Signed Integer Representation Example r =2, n=3 Number Sign-Mag. 1's Comp. 2's Comp We need a sign bit with 1 s and 2 s complements to distinguish between positive and negative numbers. Chapter 4 26
27 Signed 2 s Complement Arithmetic Addition: 1. Add the numbers including the sign bits, discarding a carry out of the sign bits 2. If the sign bits were the same for both numbers and the sign of the result is different, an overflow has occurred. 3. The sign of the result is computed in step 1. Subtraction: Form the complement of the number you are subtracting and follow the rules for addition. Chapter 4 27
28 Signed 2 s Complement Examples Example 1: Example 2: Chapter 4 28
29 2 s Complement Adder/Subtractor Subtraction can be done by addition of the 2's Complement. 1. Complement each bit (1's Complement.) 2. Add 1 to the result. The circuit shown computes A + B and A B: For S = 1, subtract, the 2 s complement of B is formed by using XORs to form the 1 s comp and adding the 1 applied to C 0. For S = 0, add, B is passed through unchanged C 4 B 3 C 3 C 2 C 1 C 0 FA FA FA FA S 3 A 3 B 2 A 2 B 1 A 1 B 0 A 0 S 2 S 1 S 0 S Chapter 4 29
30 Overflow Detection Overflow occurs if n + 1 bits are required to contain the result from an n-bit addition or subtraction Overflow can occur for: Addition of two operands with the same sign Subtraction of operands with different signs Signed number overflow cases with correct result sign Detection can be performed by examining the result signs which should match the signs of the top operand Chapter 4 30
31 Overflow Detection Signed number cases with carries C n and C n-1 shown for correct result signs: Signed number cases with carries shown for erroneous result signs (indicating overflow): Simplest way to implement overflow V = C n C n -1 Chapter 4 31
32 Other Arithmetic Functions Convenient to design the functional blocks by contraction - removal of redundancy from circuit to which input fixing has been applied Functions Incrementing Decrementing Multiplication by Constant Zero Fill and Extension Chapter 4 32
33 Design by Contraction Contraction is a technique for simplifying the logic in a functional block to implement a different function The new function must be realizable from the original function by applying rudimentary functions to its inputs Contraction is treated here only for application of 0s and 1s (not for X and X) After application of 0s and 1s, equations or the logic diagram are simplified by using rules given on pages of the text. Chapter 4 33
34 Design by Contraction Example Contraction of a ripple carry adder to incrementer for n = 3 Set B = 001 The middle cell can be repeated to make an incrementer with n > 3. Chapter 4 34
35 Incrementing & Decrementing Incrementing Adding a fixed value to an arithmetic variable Fixed value is often 1, called counting (up) Examples: A + 1, B + 4 Functional block is called incrementer Decrementing Subtracting a fixed value from an arithmetic variable Fixed value is often 1, called counting (down) Examples: A - 1, B - 4 Functional block is called decrementer Chapter 4 35
36 Multiplication/Division by 2 n (a) Multiplication by 100 Shift left by 2 (b) Division by 100 Shift right by 2 Remainder preserved C 5 B 3 0 C 3 C 4 B 2 0 C 2 B 3 B 2 B 1 B 0 C 3 B 1 C 1 (a) 0 0 C 2 C 1 C 0 B 0 C 0 C 2 1 C 2 2 (b) Chapter 4 36
37 Multiplication by a Constant Multiplication of B(3:0) by 101 B 3 B 2 B 1 B B 3 B 2 B 1 B 0 Carry output 4-bit Adder Sum C 6 C 5 C 4 C 3 C 2 C 1 C 0 Chapter 4 37
38 Zero Fill Zero fill - filling an m-bit operand with 0s to become an n-bit operand with n > m Filling usually is applied to the MSB end of the operand, but can also be done on the LSB end Example: filled to 16 bits MSB end: LSB end: Chapter 4 38
39 Extension Extension - increase in the number of bits at the MSB end of an operand by using a complement representation Copies the MSB of the operand into the new positions Positive operand example extended to 16 bits: Negative operand example extended to 16 bits: Chapter 4 39
Chapter 3: part 3 Binary Subtraction
 Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
ECE/Comp Sci 352 Digital Systems Fundamentals. Charles R. Kime Section 2 Fall Logic and Computer Design Fundamentals
 University of Wisconsin - Madison ECE/Comp Sci 352 Digital Systems Fundamentals Charles R. Kime Section 2 Fall 2001 Chapter 3 Combinational Logic Design Part 4 Charles Kime & Thomas Kaminski Complements
University of Wisconsin - Madison ECE/Comp Sci 352 Digital Systems Fundamentals Charles R. Kime Section 2 Fall 2001 Chapter 3 Combinational Logic Design Part 4 Charles Kime & Thomas Kaminski Complements
Chapter 3 Part 2 Combinational Logic Design
 University of Wisconsin - Madison ECE/Comp Sci 352 Digital Systems Fundamentals Kewal K. Saluja and Yu Hen Hu Spring 2002 Chapter 3 Part 2 Combinational Logic Design Originals by: Charles R. Kime and Tom
University of Wisconsin - Madison ECE/Comp Sci 352 Digital Systems Fundamentals Kewal K. Saluja and Yu Hen Hu Spring 2002 Chapter 3 Part 2 Combinational Logic Design Originals by: Charles R. Kime and Tom
Binary Addition. Add the binary numbers and and show the equivalent decimal addition.
 Binary Addition The rules for binary addition are 0 + 0 = 0 Sum = 0, carry = 0 0 + 1 = 0 Sum = 1, carry = 0 1 + 0 = 0 Sum = 1, carry = 0 1 + 1 = 10 Sum = 0, carry = 1 When an input carry = 1 due to a previous
Binary Addition The rules for binary addition are 0 + 0 = 0 Sum = 0, carry = 0 0 + 1 = 0 Sum = 1, carry = 0 1 + 0 = 0 Sum = 1, carry = 0 1 + 1 = 10 Sum = 0, carry = 1 When an input carry = 1 due to a previous
Chapter 4 Arithmetic
 Computer Eng 1 (ECE290) Chapter 4 Arithmetic Functions and Circuits HOANG Trang Reference: 2008 Pearson Education, Inc. Lecture note of Prof.Donna J.Brown Overview Binary adders Half and full adders Ripple
Computer Eng 1 (ECE290) Chapter 4 Arithmetic Functions and Circuits HOANG Trang Reference: 2008 Pearson Education, Inc. Lecture note of Prof.Donna J.Brown Overview Binary adders Half and full adders Ripple
Chapter 3 Part 2 Combinational Logic Design
 University of Wisconsin - Madison EE/omp ci 352 Digital ystems Fundamentals Kewal K. aluja and u Hen Hu pring 2002 hapter 3 Part 2 ombinational Logic Design Originals by: harles R. Kime and Tom Kamisnski
University of Wisconsin - Madison EE/omp ci 352 Digital ystems Fundamentals Kewal K. aluja and u Hen Hu pring 2002 hapter 3 Part 2 ombinational Logic Design Originals by: harles R. Kime and Tom Kamisnski
Lecture Topics. Announcements. Today: Integer Arithmetic (P&H ) Next: continued. Consulting hours. Introduction to Sim. Milestone #1 (due 1/26)
 Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: continued 1 Announcements Consulting hours Introduction to Sim Milestone #1 (due 1/26) 2 1 Overview: Integer Operations Internal representation
Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: continued 1 Announcements Consulting hours Introduction to Sim Milestone #1 (due 1/26) 2 1 Overview: Integer Operations Internal representation
CHAPTER V NUMBER SYSTEMS AND ARITHMETIC
 CHAPTER V-1 CHAPTER V CHAPTER V NUMBER SYSTEMS AND ARITHMETIC CHAPTER V-2 NUMBER SYSTEMS RADIX-R REPRESENTATION Decimal number expansion 73625 10 = ( 7 10 4 ) + ( 3 10 3 ) + ( 6 10 2 ) + ( 2 10 1 ) +(
CHAPTER V-1 CHAPTER V CHAPTER V NUMBER SYSTEMS AND ARITHMETIC CHAPTER V-2 NUMBER SYSTEMS RADIX-R REPRESENTATION Decimal number expansion 73625 10 = ( 7 10 4 ) + ( 3 10 3 ) + ( 6 10 2 ) + ( 2 10 1 ) +(
carry in carry 1101 carry carry
 Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
Binary Adders: Half Adders and Full Adders
 Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
Principles of Computer Architecture. Chapter 3: Arithmetic
 3-1 Chapter 3 - Arithmetic Principles of Computer Architecture Miles Murdocca and Vincent Heuring Chapter 3: Arithmetic 3-2 Chapter 3 - Arithmetic 3.1 Overview Chapter Contents 3.2 Fixed Point Addition
3-1 Chapter 3 - Arithmetic Principles of Computer Architecture Miles Murdocca and Vincent Heuring Chapter 3: Arithmetic 3-2 Chapter 3 - Arithmetic 3.1 Overview Chapter Contents 3.2 Fixed Point Addition
COMPUTER ARITHMETIC (Part 1)
 Eastern Mediterranean University School of Computing and Technology ITEC255 Computer Organization & Architecture COMPUTER ARITHMETIC (Part 1) Introduction The two principal concerns for computer arithmetic
Eastern Mediterranean University School of Computing and Technology ITEC255 Computer Organization & Architecture COMPUTER ARITHMETIC (Part 1) Introduction The two principal concerns for computer arithmetic
Chapter 10 - Computer Arithmetic
 Chapter 10 - Computer Arithmetic Luis Tarrataca luis.tarrataca@gmail.com CEFET-RJ L. Tarrataca Chapter 10 - Computer Arithmetic 1 / 126 1 Motivation 2 Arithmetic and Logic Unit 3 Integer representation
Chapter 10 - Computer Arithmetic Luis Tarrataca luis.tarrataca@gmail.com CEFET-RJ L. Tarrataca Chapter 10 - Computer Arithmetic 1 / 126 1 Motivation 2 Arithmetic and Logic Unit 3 Integer representation
World Inside a Computer is Binary
 C Programming 1 Representation of int data World Inside a Computer is Binary C Programming 2 Decimal Number System Basic symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Radix-10 positional number system. The radix
C Programming 1 Representation of int data World Inside a Computer is Binary C Programming 2 Decimal Number System Basic symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Radix-10 positional number system. The radix
Semester Transition Point. EE 109 Unit 11 Binary Arithmetic. Binary Arithmetic ARITHMETIC
 1 2 Semester Transition Point EE 109 Unit 11 Binary Arithmetic At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
1 2 Semester Transition Point EE 109 Unit 11 Binary Arithmetic At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
Advanced Computer Architecture-CS501
 Advanced Computer Architecture Lecture No. 34 Reading Material Vincent P. Heuring & Harry F. Jordan Chapter 6 Computer Systems Design and Architecture 6.1, 6.2 Summary Introduction to ALSU Radix Conversion
Advanced Computer Architecture Lecture No. 34 Reading Material Vincent P. Heuring & Harry F. Jordan Chapter 6 Computer Systems Design and Architecture 6.1, 6.2 Summary Introduction to ALSU Radix Conversion
Digital Systems and Binary Numbers
 Digital Systems and Binary Numbers Mano & Ciletti Chapter 1 By Suleyman TOSUN Ankara University Outline Digital Systems Binary Numbers Number-Base Conversions Octal and Hexadecimal Numbers Complements
Digital Systems and Binary Numbers Mano & Ciletti Chapter 1 By Suleyman TOSUN Ankara University Outline Digital Systems Binary Numbers Number-Base Conversions Octal and Hexadecimal Numbers Complements
Register Transfer Language and Microoperations (Part 2)
 Register Transfer Language and Microoperations (Part 2) Adapted by Dr. Adel Ammar Computer Organization 1 MICROOPERATIONS Computer system microoperations are of four types: Register transfer microoperations
Register Transfer Language and Microoperations (Part 2) Adapted by Dr. Adel Ammar Computer Organization 1 MICROOPERATIONS Computer system microoperations are of four types: Register transfer microoperations
(+A) + ( B) + (A B) (B A) + (A B) ( A) + (+ B) (A B) + (B A) + (A B) (+ A) (+ B) + (A - B) (B A) + (A B) ( A) ( B) (A B) + (B A) + (A B)
 COMPUTER ARITHMETIC 1. Addition and Subtraction of Unsigned Numbers The direct method of subtraction taught in elementary schools uses the borrowconcept. In this method we borrow a 1 from a higher significant
COMPUTER ARITHMETIC 1. Addition and Subtraction of Unsigned Numbers The direct method of subtraction taught in elementary schools uses the borrowconcept. In this method we borrow a 1 from a higher significant
Number System. Introduction. Decimal Numbers
 Number System Introduction Number systems provide the basis for all operations in information processing systems. In a number system the information is divided into a group of symbols; for example, 26
Number System Introduction Number systems provide the basis for all operations in information processing systems. In a number system the information is divided into a group of symbols; for example, 26
Arithmetic Operations
 Arithmetic Operations Arithmetic Operations addition subtraction multiplication division Each of these operations on the integer representations: unsigned two's complement 1 Addition One bit of binary
Arithmetic Operations Arithmetic Operations addition subtraction multiplication division Each of these operations on the integer representations: unsigned two's complement 1 Addition One bit of binary
10.1. Unit 10. Signed Representation Systems Binary Arithmetic
 0. Unit 0 Signed Representation Systems Binary Arithmetic 0.2 BINARY REPRESENTATION SYSTEMS REVIEW 0.3 Interpreting Binary Strings Given a string of s and 0 s, you need to know the representation system
0. Unit 0 Signed Representation Systems Binary Arithmetic 0.2 BINARY REPRESENTATION SYSTEMS REVIEW 0.3 Interpreting Binary Strings Given a string of s and 0 s, you need to know the representation system
Experiment 7 Arithmetic Circuits Design and Implementation
 Experiment 7 Arithmetic Circuits Design and Implementation Introduction: Addition is just what you would expect in computers. Digits are added bit by bit from right to left, with carries passed to the
Experiment 7 Arithmetic Circuits Design and Implementation Introduction: Addition is just what you would expect in computers. Digits are added bit by bit from right to left, with carries passed to the
II/IV B.Tech (Regular/Supplementary) DEGREE EXAMINATION. Answer ONE question from each unit.
 Hall Ticket Number: 14CS IT303 November, 2017 Third Semester Time: Three Hours Answer Question No.1 compulsorily. II/IV B.Tech (Regular/Supplementary) DEGREE EXAMINATION Common for CSE & IT Digital Logic
Hall Ticket Number: 14CS IT303 November, 2017 Third Semester Time: Three Hours Answer Question No.1 compulsorily. II/IV B.Tech (Regular/Supplementary) DEGREE EXAMINATION Common for CSE & IT Digital Logic
Computer Architecture and Organization
 3-1 Chapter 3 - Arithmetic Computer Architecture and Organization Miles Murdocca and Vincent Heuring Chapter 3 Arithmetic 3-2 Chapter 3 - Arithmetic Chapter Contents 3.1 Fixed Point Addition and Subtraction
3-1 Chapter 3 - Arithmetic Computer Architecture and Organization Miles Murdocca and Vincent Heuring Chapter 3 Arithmetic 3-2 Chapter 3 - Arithmetic Chapter Contents 3.1 Fixed Point Addition and Subtraction
UNIT IV: DATA PATH DESIGN
 UNIT IV: DATA PATH DESIGN Agenda Introduc/on Fixed Point Arithme/c Addi/on Subtrac/on Mul/plica/on & Serial mul/plier Division & Serial Divider Two s Complement (Addi/on, Subtrac/on) Booth s algorithm
UNIT IV: DATA PATH DESIGN Agenda Introduc/on Fixed Point Arithme/c Addi/on Subtrac/on Mul/plica/on & Serial mul/plier Division & Serial Divider Two s Complement (Addi/on, Subtrac/on) Booth s algorithm
*Instruction Matters: Purdue Academic Course Transformation. Introduction to Digital System Design. Module 4 Arithmetic and Computer Logic Circuits
 Purdue IM:PACT* Fall 2018 Edition *Instruction Matters: Purdue Academic Course Transformation Introduction to Digital System Design Module 4 Arithmetic and Computer Logic Circuits Glossary of Common Terms
Purdue IM:PACT* Fall 2018 Edition *Instruction Matters: Purdue Academic Course Transformation Introduction to Digital System Design Module 4 Arithmetic and Computer Logic Circuits Glossary of Common Terms
DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS
 C H A P T E R 6 DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS OUTLINE 6- Binary Addition 6-2 Representing Signed Numbers 6-3 Addition in the 2 s- Complement System 6-4 Subtraction in the 2 s- Complement
C H A P T E R 6 DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS OUTLINE 6- Binary Addition 6-2 Representing Signed Numbers 6-3 Addition in the 2 s- Complement System 6-4 Subtraction in the 2 s- Complement
Computer Architecture and Organization: L04: Micro-operations
 Computer Architecture and Organization: L4: Micro-operations By: A. H. Abdul Hafez Abdul.hafez@hku.edu.tr, ah.abdulhafez@gmail.com, hafez@research.iiit.ac.in 1 Outlines 1. Arithmetic microoperation 2.
Computer Architecture and Organization: L4: Micro-operations By: A. H. Abdul Hafez Abdul.hafez@hku.edu.tr, ah.abdulhafez@gmail.com, hafez@research.iiit.ac.in 1 Outlines 1. Arithmetic microoperation 2.
EE 109 Unit 6 Binary Arithmetic
 EE 109 Unit 6 Binary Arithmetic 1 2 Semester Transition Point At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
EE 109 Unit 6 Binary Arithmetic 1 2 Semester Transition Point At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
Basic Arithmetic (adding and subtracting)
 Basic Arithmetic (adding and subtracting) Digital logic to show add/subtract Boolean algebra abstraction of physical, analog circuit behavior 1 0 CPU components ALU logic circuits logic gates transistors
Basic Arithmetic (adding and subtracting) Digital logic to show add/subtract Boolean algebra abstraction of physical, analog circuit behavior 1 0 CPU components ALU logic circuits logic gates transistors
Chapter 10 Binary Arithmetics
 27..27 Chapter Binary Arithmetics Dr.-Ing. Stefan Werner Table of content Chapter : Switching Algebra Chapter 2: Logical Levels, Timing & Delays Chapter 3: Karnaugh-Veitch-Maps Chapter 4: Combinational
27..27 Chapter Binary Arithmetics Dr.-Ing. Stefan Werner Table of content Chapter : Switching Algebra Chapter 2: Logical Levels, Timing & Delays Chapter 3: Karnaugh-Veitch-Maps Chapter 4: Combinational
Digital Fundamentals
 Digital Fundamentals Tenth Edition Floyd Chapter 2 2009 Pearson Education, Upper 2008 Pearson Saddle River, Education NJ 07458. All Rights Reserved Decimal Numbers The position of each digit in a weighted
Digital Fundamentals Tenth Edition Floyd Chapter 2 2009 Pearson Education, Upper 2008 Pearson Saddle River, Education NJ 07458. All Rights Reserved Decimal Numbers The position of each digit in a weighted
COMBINATIONAL LOGIC CIRCUITS
 COMBINATIONAL LOGIC CIRCUITS 4.1 INTRODUCTION The digital system consists of two types of circuits, namely: (i) Combinational circuits and (ii) Sequential circuits A combinational circuit consists of logic
COMBINATIONAL LOGIC CIRCUITS 4.1 INTRODUCTION The digital system consists of two types of circuits, namely: (i) Combinational circuits and (ii) Sequential circuits A combinational circuit consists of logic
Arithmetic Processing
 CS/EE 5830/6830 VLSI ARCHITECTURE Chapter 1 Basic Number Representations and Arithmetic Algorithms Arithmetic Processing AP = (operands, operation, results, conditions, singularities) Operands are: Set
CS/EE 5830/6830 VLSI ARCHITECTURE Chapter 1 Basic Number Representations and Arithmetic Algorithms Arithmetic Processing AP = (operands, operation, results, conditions, singularities) Operands are: Set
Korea University of Technology and Education
 MEC52 디지털공학 Binary Systems Jee-Hwan Ryu School of Mechanical Engineering Binary Numbers a 5 a 4 a 3 a 2 a a.a - a -2 a -3 base or radix = a n r n a n- r n-...a 2 r 2 a ra a - r - a -2 r -2...a -m r -m
MEC52 디지털공학 Binary Systems Jee-Hwan Ryu School of Mechanical Engineering Binary Numbers a 5 a 4 a 3 a 2 a a.a - a -2 a -3 base or radix = a n r n a n- r n-...a 2 r 2 a ra a - r - a -2 r -2...a -m r -m
Chapter 2: Number Systems
 Chapter 2: Number Systems Logic circuits are used to generate and transmit 1s and 0s to compute and convey information. This two-valued number system is called binary. As presented earlier, there are many
Chapter 2: Number Systems Logic circuits are used to generate and transmit 1s and 0s to compute and convey information. This two-valued number system is called binary. As presented earlier, there are many
MC1601 Computer Organization
 MC1601 Computer Organization Unit 1 : Digital Fundamentals Lesson1 : Number Systems and Conversions (KSB) (MCA) (2009-12/ODD) (2009-10/1 A&B) Coverage - Lesson1 Shows how various data types found in digital
MC1601 Computer Organization Unit 1 : Digital Fundamentals Lesson1 : Number Systems and Conversions (KSB) (MCA) (2009-12/ODD) (2009-10/1 A&B) Coverage - Lesson1 Shows how various data types found in digital
ECE468 Computer Organization & Architecture. The Design Process & ALU Design
 ECE6 Computer Organization & Architecture The Design Process & Design The Design Process "To Design Is To Represent" Design activity yields description/representation of an object -- Traditional craftsman
ECE6 Computer Organization & Architecture The Design Process & Design The Design Process "To Design Is To Represent" Design activity yields description/representation of an object -- Traditional craftsman
Chap.3 3. Chap reduces the complexity required to represent the schematic diagram of a circuit Library
 3.1 Combinational Circuits 2 Chap 3. logic circuits for digital systems: combinational vs sequential Combinational Logic Design Combinational Circuit (Chap 3) outputs are determined by the present applied
3.1 Combinational Circuits 2 Chap 3. logic circuits for digital systems: combinational vs sequential Combinational Logic Design Combinational Circuit (Chap 3) outputs are determined by the present applied
Arithmetic and Logical Operations
 Arithmetic and Logical Operations 2 CMPE2c x +y + sum Or in tabular form Binary Addition Carry Out Sum B A Carry In Binary Addition And as a full adder a b co ci sum 4-bit Ripple-Carry adder: Carry values
Arithmetic and Logical Operations 2 CMPE2c x +y + sum Or in tabular form Binary Addition Carry Out Sum B A Carry In Binary Addition And as a full adder a b co ci sum 4-bit Ripple-Carry adder: Carry values
UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT
 UNIT-III 1 KNREDDY UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT Register Transfer: Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Micro operations Logic
UNIT-III 1 KNREDDY UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT Register Transfer: Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Micro operations Logic
CO Computer Architecture and Programming Languages CAPL. Lecture 9
 CO20-320241 Computer Architecture and Programming Languages CAPL Lecture 9 Dr. Kinga Lipskoch Fall 2017 A Four-bit Number Circle CAPL Fall 2017 2 / 38 Functional Parts of an ALU CAPL Fall 2017 3 / 38 Addition
CO20-320241 Computer Architecture and Programming Languages CAPL Lecture 9 Dr. Kinga Lipskoch Fall 2017 A Four-bit Number Circle CAPL Fall 2017 2 / 38 Functional Parts of an ALU CAPL Fall 2017 3 / 38 Addition
Combinational Logic II
 Combinational Logic II Ranga Rodrigo July 26, 2009 1 Binary Adder-Subtractor Digital computers perform variety of information processing tasks. Among the functions encountered are the various arithmetic
Combinational Logic II Ranga Rodrigo July 26, 2009 1 Binary Adder-Subtractor Digital computers perform variety of information processing tasks. Among the functions encountered are the various arithmetic
Chapter 4. Operations on Data
 Chapter 4 Operations on Data 1 OBJECTIVES After reading this chapter, the reader should be able to: List the three categories of operations performed on data. Perform unary and binary logic operations
Chapter 4 Operations on Data 1 OBJECTIVES After reading this chapter, the reader should be able to: List the three categories of operations performed on data. Perform unary and binary logic operations
LOGIC CIRCUITS. Kirti P_Didital Design 1
 LOGIC CIRCUITS Kirti P_Didital Design 1 Introduction The digital system consists of two types of circuits, namely (i) Combinational circuits and (ii) Sequential circuit A combinational circuit consists
LOGIC CIRCUITS Kirti P_Didital Design 1 Introduction The digital system consists of two types of circuits, namely (i) Combinational circuits and (ii) Sequential circuit A combinational circuit consists
Number representations
 Number representations Number bases Three number bases are of interest: Binary, Octal and Hexadecimal. We look briefly at conversions among them and between each of them and decimal. Binary Base-two, or
Number representations Number bases Three number bases are of interest: Binary, Octal and Hexadecimal. We look briefly at conversions among them and between each of them and decimal. Binary Base-two, or
CS/COE 0447 Example Problems for Exam 2 Spring 2011
 CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
2.1. Unit 2. Integer Operations (Arithmetic, Overflow, Bitwise Logic, Shifting)
 2.1 Unit 2 Integer Operations (Arithmetic, Overflow, Bitwise Logic, Shifting) 2.2 Skills & Outcomes You should know and be able to apply the following skills with confidence Perform addition & subtraction
2.1 Unit 2 Integer Operations (Arithmetic, Overflow, Bitwise Logic, Shifting) 2.2 Skills & Outcomes You should know and be able to apply the following skills with confidence Perform addition & subtraction
Logic Circuits I ECE 1411 Thursday 4:45pm-7:20pm. Nathan Pihlstrom.
 Logic Circuits I ECE 1411 Thursday 4:45pm-7:20pm Nathan Pihlstrom www.uccs.edu/~npihlstr My Background B.S.E.E. from Colorado State University M.S.E.E. from Colorado State University M.B.A. from UCCS Ford
Logic Circuits I ECE 1411 Thursday 4:45pm-7:20pm Nathan Pihlstrom www.uccs.edu/~npihlstr My Background B.S.E.E. from Colorado State University M.S.E.E. from Colorado State University M.B.A. from UCCS Ford
CHW 261: Logic Design
 CHW 261: Logic Design Instructors: Prof. Hala Zayed Dr. Ahmed Shalaby http://www.bu.edu.eg/staff/halazayed14 http://bu.edu.eg/staff/ahmedshalaby14# Slide 1 Slide 2 Slide 3 Digital Fundamentals CHAPTER
CHW 261: Logic Design Instructors: Prof. Hala Zayed Dr. Ahmed Shalaby http://www.bu.edu.eg/staff/halazayed14 http://bu.edu.eg/staff/ahmedshalaby14# Slide 1 Slide 2 Slide 3 Digital Fundamentals CHAPTER
Number Systems. Readings: , Problem: Implement simple pocket calculator Need: Display, adders & subtractors, inputs
 Number Systems Readings: 3-3.3.3, 3.3.5 Problem: Implement simple pocket calculator Need: Display, adders & subtractors, inputs Display: Seven segment displays Inputs: Switches Missing: Way to implement
Number Systems Readings: 3-3.3.3, 3.3.5 Problem: Implement simple pocket calculator Need: Display, adders & subtractors, inputs Display: Seven segment displays Inputs: Switches Missing: Way to implement
CO212 Lecture 10: Arithmetic & Logical Unit
 CO212 Lecture 10: Arithmetic & Logical Unit Shobhanjana Kalita, Dept. of CSE, Tezpur University Slides courtesy: Computer Architecture and Organization, 9 th Ed, W. Stallings Integer Representation For
CO212 Lecture 10: Arithmetic & Logical Unit Shobhanjana Kalita, Dept. of CSE, Tezpur University Slides courtesy: Computer Architecture and Organization, 9 th Ed, W. Stallings Integer Representation For
Department of Electrical and Computer Engineering University of Wisconsin - Madison. ECE/CS 352 Digital System Fundamentals.
 Department of Electrical and Computer Engineering University of Wisconsin - Madison ECE/C 352 Digital ystem Fundamentals Quiz #2 Thursday, March 7, 22, 7:15--8:3PM 1. (15 points) (a) (5 points) NAND, NOR
Department of Electrical and Computer Engineering University of Wisconsin - Madison ECE/C 352 Digital ystem Fundamentals Quiz #2 Thursday, March 7, 22, 7:15--8:3PM 1. (15 points) (a) (5 points) NAND, NOR
1. Mark the correct statement(s)
 1. Mark the correct statement(s) 1.1 A theorem in Boolean algebra: a) Can easily be proved by e.g. logic induction b) Is a logical statement that is assumed to be true, c) Can be contradicted by another
1. Mark the correct statement(s) 1.1 A theorem in Boolean algebra: a) Can easily be proved by e.g. logic induction b) Is a logical statement that is assumed to be true, c) Can be contradicted by another
Kinds Of Data CHAPTER 3 DATA REPRESENTATION. Numbers Are Different! Positional Number Systems. Text. Numbers. Other
 Kinds Of Data CHAPTER 3 DATA REPRESENTATION Numbers Integers Unsigned Signed Reals Fixed-Point Floating-Point Binary-Coded Decimal Text ASCII Characters Strings Other Graphics Images Video Audio Numbers
Kinds Of Data CHAPTER 3 DATA REPRESENTATION Numbers Integers Unsigned Signed Reals Fixed-Point Floating-Point Binary-Coded Decimal Text ASCII Characters Strings Other Graphics Images Video Audio Numbers
MGU-BCA-205- Second Sem- Core VI- Fundamentals of Digital Systems- MCQ s. 2. Why the decimal number system is also called as positional number system?
 MGU-BCA-205- Second Sem- Core VI- Fundamentals of Digital Systems- MCQ s Unit-1 Number Systems 1. What does a decimal number represents? A. Quality B. Quantity C. Position D. None of the above 2. Why the
MGU-BCA-205- Second Sem- Core VI- Fundamentals of Digital Systems- MCQ s Unit-1 Number Systems 1. What does a decimal number represents? A. Quality B. Quantity C. Position D. None of the above 2. Why the
BINARY SYSTEM. Binary system is used in digital systems because it is:
 CHAPTER 2 CHAPTER CONTENTS 2.1 Binary System 2.2 Binary Arithmetic Operation 2.3 Signed & Unsigned Numbers 2.4 Arithmetic Operations of Signed Numbers 2.5 Hexadecimal Number System 2.6 Octal Number System
CHAPTER 2 CHAPTER CONTENTS 2.1 Binary System 2.2 Binary Arithmetic Operation 2.3 Signed & Unsigned Numbers 2.4 Arithmetic Operations of Signed Numbers 2.5 Hexadecimal Number System 2.6 Octal Number System
Binary Adders. Ripple-Carry Adder
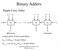 Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Module 2: Computer Arithmetic
 Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
A complement number system is used to represent positive and negative integers. A complement number system is based on a fixed length representation
 Complement Number Systems A complement number system is used to represent positive and negative integers A complement number system is based on a fixed length representation of numbers Pretend that integers
Complement Number Systems A complement number system is used to represent positive and negative integers A complement number system is based on a fixed length representation of numbers Pretend that integers
Chapter 1. Digital Systems and Binary Numbers
 Chapter 1. Digital Systems and Binary Numbers Tong In Oh 1 1.1 Digital Systems Digital age Characteristic of digital system Generality and flexibility Represent and manipulate discrete elements of information
Chapter 1. Digital Systems and Binary Numbers Tong In Oh 1 1.1 Digital Systems Digital age Characteristic of digital system Generality and flexibility Represent and manipulate discrete elements of information
Digital Arithmetic. Digital Arithmetic: Operations and Circuits Dr. Farahmand
 Digital Arithmetic Digital Arithmetic: Operations and Circuits Dr. Farahmand Binary Arithmetic Digital circuits are frequently used for arithmetic operations Fundamental arithmetic operations on binary
Digital Arithmetic Digital Arithmetic: Operations and Circuits Dr. Farahmand Binary Arithmetic Digital circuits are frequently used for arithmetic operations Fundamental arithmetic operations on binary
CHAPTER 6 ARITHMETIC, LOGIC INSTRUCTIONS, AND PROGRAMS
 CHAPTER 6 ARITHMETIC, LOGIC INSTRUCTIONS, AND PROGRAMS Addition of Unsigned Numbers The instruction ADD is used to add two operands Destination operand is always in register A Source operand can be a register,
CHAPTER 6 ARITHMETIC, LOGIC INSTRUCTIONS, AND PROGRAMS Addition of Unsigned Numbers The instruction ADD is used to add two operands Destination operand is always in register A Source operand can be a register,
ECEN 468 Advanced Logic Design
 ECEN 468 Advanced Logic Design Lecture 26: Verilog Operators ECEN 468 Lecture 26 Operators Operator Number of Operands Result Arithmetic 2 Binary word Bitwise 2 Binary word Reduction 1 Bit Logical 2 Boolean
ECEN 468 Advanced Logic Design Lecture 26: Verilog Operators ECEN 468 Lecture 26 Operators Operator Number of Operands Result Arithmetic 2 Binary word Bitwise 2 Binary word Reduction 1 Bit Logical 2 Boolean
Number Systems Base r
 King Fahd University of Petroleum & Minerals Computer Engineering Dept COE 2 Fundamentals of Computer Engineering Term 22 Dr. Ashraf S. Hasan Mahmoud Rm 22-44 Ext. 724 Email: ashraf@ccse.kfupm.edu.sa 3/7/23
King Fahd University of Petroleum & Minerals Computer Engineering Dept COE 2 Fundamentals of Computer Engineering Term 22 Dr. Ashraf S. Hasan Mahmoud Rm 22-44 Ext. 724 Email: ashraf@ccse.kfupm.edu.sa 3/7/23
Digital Systems and Binary Numbers
 Digital Systems and Binary Numbers Prof. Wangrok Oh Dept. of Information Communications Eng. Chungnam National University Prof. Wangrok Oh(CNU) 1 / 51 Overview 1 Course Summary 2 Binary Numbers 3 Number-Base
Digital Systems and Binary Numbers Prof. Wangrok Oh Dept. of Information Communications Eng. Chungnam National University Prof. Wangrok Oh(CNU) 1 / 51 Overview 1 Course Summary 2 Binary Numbers 3 Number-Base
Lecture (02) Operations on numbering systems
 Lecture (02) Operations on numbering systems By: Dr. Ahmed ElShafee ١ Dr. Ahmed ElShafee, ACU : Spring 2018, CSE202 Logic Design I Complements of a number Complements are used in digital computers to simplify
Lecture (02) Operations on numbering systems By: Dr. Ahmed ElShafee ١ Dr. Ahmed ElShafee, ACU : Spring 2018, CSE202 Logic Design I Complements of a number Complements are used in digital computers to simplify
Number Systems. Both numbers are positive
 Number Systems Range of Numbers and Overflow When arithmetic operation such as Addition, Subtraction, Multiplication and Division are performed on numbers the results generated may exceed the range of
Number Systems Range of Numbers and Overflow When arithmetic operation such as Addition, Subtraction, Multiplication and Division are performed on numbers the results generated may exceed the range of
COMP 303 Computer Architecture Lecture 6
 COMP 303 Computer Architecture Lecture 6 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 0000 0000 1000 Product 01001000 = 72 n bits x n bits =
COMP 303 Computer Architecture Lecture 6 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 0000 0000 1000 Product 01001000 = 72 n bits x n bits =
COMPUTER ARCHITECTURE AND ORGANIZATION Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital
 Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital hardware modules that accomplish a specific information-processing task. Digital systems vary in
Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital hardware modules that accomplish a specific information-processing task. Digital systems vary in
COE 202: Digital Logic Design Number Systems Part 2. Dr. Ahmad Almulhem ahmadsm AT kfupm Phone: Office:
 COE 0: Digital Logic Design Number Systems Part Dr. Ahmad Almulhem Email: ahmadsm AT kfupm Phone: 860-7554 Office: -34 Objectives Arithmetic operations: Binary number system Other number systems Base Conversion
COE 0: Digital Logic Design Number Systems Part Dr. Ahmad Almulhem Email: ahmadsm AT kfupm Phone: 860-7554 Office: -34 Objectives Arithmetic operations: Binary number system Other number systems Base Conversion
Positional Number System
 Positional Number System A number is represented by a string of digits where each digit position has an associated weight. The weight is based on the radix of the number system. Some common radices: Decimal.
Positional Number System A number is represented by a string of digits where each digit position has an associated weight. The weight is based on the radix of the number system. Some common radices: Decimal.
Arithmetic Circuits. Nurul Hazlina Adder 2. Multiplier 3. Arithmetic Logic Unit (ALU) 4. HDL for Arithmetic Circuit
 Nurul Hazlina 1 1. Adder 2. Multiplier 3. Arithmetic Logic Unit (ALU) 4. HDL for Arithmetic Circuit Nurul Hazlina 2 Introduction 1. Digital circuits are frequently used for arithmetic operations 2. Fundamental
Nurul Hazlina 1 1. Adder 2. Multiplier 3. Arithmetic Logic Unit (ALU) 4. HDL for Arithmetic Circuit Nurul Hazlina 2 Introduction 1. Digital circuits are frequently used for arithmetic operations 2. Fundamental
INF2270 Spring Philipp Häfliger. Lecture 4: Signed Binaries and Arithmetic
 INF2270 Spring 2010 Philipp Häfliger Lecture 4: Signed Binaries and Arithmetic content Karnaugh maps revisited Binary Addition Signed Binary Numbers Binary Subtraction Arithmetic Right-Shift and Bit Number
INF2270 Spring 2010 Philipp Häfliger Lecture 4: Signed Binaries and Arithmetic content Karnaugh maps revisited Binary Addition Signed Binary Numbers Binary Subtraction Arithmetic Right-Shift and Bit Number
Lecture 2: Number Systems
 Lecture 2: Number Systems Syed M. Mahmud, Ph.D ECE Department Wayne State University Original Source: Prof. Russell Tessier of University of Massachusetts Aby George of Wayne State University Contents
Lecture 2: Number Systems Syed M. Mahmud, Ph.D ECE Department Wayne State University Original Source: Prof. Russell Tessier of University of Massachusetts Aby George of Wayne State University Contents
Number Systems Standard positional representation of numbers: An unsigned number with whole and fraction portions is represented as:
 N Number Systems Standard positional representation of numbers: An unsigned number with whole and fraction portions is represented as: a n a a a The value of this number is given by: = a n Ka a a a a a
N Number Systems Standard positional representation of numbers: An unsigned number with whole and fraction portions is represented as: a n a a a The value of this number is given by: = a n Ka a a a a a
CPE 323 REVIEW DATA TYPES AND NUMBER REPRESENTATIONS IN MODERN COMPUTERS
 CPE 323 REVIEW DATA TYPES AND NUMBER REPRESENTATIONS IN MODERN COMPUTERS Aleksandar Milenković The LaCASA Laboratory, ECE Department, The University of Alabama in Huntsville Email: milenka@uah.edu Web:
CPE 323 REVIEW DATA TYPES AND NUMBER REPRESENTATIONS IN MODERN COMPUTERS Aleksandar Milenković The LaCASA Laboratory, ECE Department, The University of Alabama in Huntsville Email: milenka@uah.edu Web:
DIGITAL SYSTEM DESIGN
 DIGITAL SYSTEM DESIGN UNIT I: Introduction to Number Systems and Boolean Algebra Digital and Analog Basic Concepts, Some history of Digital Systems-Introduction to number systems, Binary numbers, Number
DIGITAL SYSTEM DESIGN UNIT I: Introduction to Number Systems and Boolean Algebra Digital and Analog Basic Concepts, Some history of Digital Systems-Introduction to number systems, Binary numbers, Number
CHAPTER 4: Register Transfer Language and Microoperations
 CS 224: Computer Organization S.KHABET CHAPTER 4: Register Transfer Language and Microoperations Outline Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Microoperations
CS 224: Computer Organization S.KHABET CHAPTER 4: Register Transfer Language and Microoperations Outline Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Microoperations
Computer Organization
 Computer Organization Register Transfer Logic Number System Department of Computer Science Missouri University of Science & Technology hurson@mst.edu 1 Decimal Numbers: Base 10 Digits: 0, 1, 2, 3, 4, 5,
Computer Organization Register Transfer Logic Number System Department of Computer Science Missouri University of Science & Technology hurson@mst.edu 1 Decimal Numbers: Base 10 Digits: 0, 1, 2, 3, 4, 5,
Computer Sc. & IT. Digital Logic. Computer Sciencee & Information Technology. 20 Rank under AIR 100. Postal Correspondence
 GATE Postal Correspondence Computer Sc. & IT 1 Digital Logic Computer Sciencee & Information Technology (CS) 20 Rank under AIR 100 Postal Correspondence Examination Oriented Theory, Practice Set Key concepts,
GATE Postal Correspondence Computer Sc. & IT 1 Digital Logic Computer Sciencee & Information Technology (CS) 20 Rank under AIR 100 Postal Correspondence Examination Oriented Theory, Practice Set Key concepts,
CHAPTER TWO. Data Representation ( M.MORRIS MANO COMPUTER SYSTEM ARCHITECTURE THIRD EDITION ) IN THIS CHAPTER
 1 CHAPTER TWO Data Representation ( M.MORRIS MANO COMPUTER SYSTEM ARCHITECTURE THIRD EDITION ) IN THIS CHAPTER 2-1 Data Types 2-2 Complements 2-3 Fixed-Point Representation 2-4 Floating-Point Representation
1 CHAPTER TWO Data Representation ( M.MORRIS MANO COMPUTER SYSTEM ARCHITECTURE THIRD EDITION ) IN THIS CHAPTER 2-1 Data Types 2-2 Complements 2-3 Fixed-Point Representation 2-4 Floating-Point Representation
COMPUTER ARCHITECTURE AND ORGANIZATION. Operation Add Magnitudes Subtract Magnitudes (+A) + ( B) + (A B) (B A) + (A B)
 Computer Arithmetic Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation problems. The Addition,
Computer Arithmetic Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation problems. The Addition,
Digital Fundamentals. CHAPTER 2 Number Systems, Operations, and Codes
 Digital Fundamentals CHAPTER 2 Number Systems, Operations, and Codes Decimal Numbers The decimal number system has ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 The decimal numbering system has a base of
Digital Fundamentals CHAPTER 2 Number Systems, Operations, and Codes Decimal Numbers The decimal number system has ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 The decimal numbering system has a base of
Number Systems CHAPTER Positional Number Systems
 CHAPTER 2 Number Systems Inside computers, information is encoded as patterns of bits because it is easy to construct electronic circuits that exhibit the two alternative states, 0 and 1. The meaning of
CHAPTER 2 Number Systems Inside computers, information is encoded as patterns of bits because it is easy to construct electronic circuits that exhibit the two alternative states, 0 and 1. The meaning of
Lecture 6: Signed Numbers & Arithmetic Circuits. BCD (Binary Coded Decimal) Points Addressed in this Lecture
 Points ddressed in this Lecture Lecture 6: Signed Numbers rithmetic Circuits Professor Peter Cheung Department of EEE, Imperial College London (Floyd 2.5-2.7, 6.1-6.7) (Tocci 6.1-6.11, 9.1-9.2, 9.4) Representing
Points ddressed in this Lecture Lecture 6: Signed Numbers rithmetic Circuits Professor Peter Cheung Department of EEE, Imperial College London (Floyd 2.5-2.7, 6.1-6.7) (Tocci 6.1-6.11, 9.1-9.2, 9.4) Representing
MYcsvtu Notes DATA REPRESENTATION. Data Types. Complements. Fixed Point Representations. Floating Point Representations. Other Binary Codes
 DATA REPRESENTATION Data Types Complements Fixed Point Representations Floating Point Representations Other Binary Codes Error Detection Codes Hamming Codes 1. DATA REPRESENTATION Information that a Computer
DATA REPRESENTATION Data Types Complements Fixed Point Representations Floating Point Representations Other Binary Codes Error Detection Codes Hamming Codes 1. DATA REPRESENTATION Information that a Computer
Number Systems and Computer Arithmetic
 Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
REGISTER TRANSFER AND MICROOPERATIONS
 1 REGISTER TRANSFER AND MICROOPERATIONS Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Microoperations Logic Microoperations Shift Microoperations Arithmetic Logic Shift
1 REGISTER TRANSFER AND MICROOPERATIONS Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Microoperations Logic Microoperations Shift Microoperations Arithmetic Logic Shift
Arithmetic Logic Unit
 Arithmetic Logic Unit A.R. Hurson Department of Computer Science Missouri University of Science & Technology A.R. Hurson 1 Arithmetic Logic Unit It is a functional bo designed to perform "basic" arithmetic,
Arithmetic Logic Unit A.R. Hurson Department of Computer Science Missouri University of Science & Technology A.R. Hurson 1 Arithmetic Logic Unit It is a functional bo designed to perform "basic" arithmetic,
CARLETON UNIVERSITY. Laboratory 2.0
 CARLETON UNIVERSITY Department of Electronics ELEC 267 Switching Circuits Jan 3, 28 Overview Laboratory 2. A 3-Bit Binary Sign-Extended Adder/Subtracter A binary adder sums two binary numbers for example
CARLETON UNIVERSITY Department of Electronics ELEC 267 Switching Circuits Jan 3, 28 Overview Laboratory 2. A 3-Bit Binary Sign-Extended Adder/Subtracter A binary adder sums two binary numbers for example
BUILDING BLOCKS OF A BASIC MICROPROCESSOR. Part 1 PowerPoint Format of Lecture 3 of Book
 BUILDING BLOCKS OF A BASIC MICROPROCESSOR Part PowerPoint Format of Lecture 3 of Book Decoder Tri-state device Full adder, full subtractor Arithmetic Logic Unit (ALU) Memories Example showing how to write
BUILDING BLOCKS OF A BASIC MICROPROCESSOR Part PowerPoint Format of Lecture 3 of Book Decoder Tri-state device Full adder, full subtractor Arithmetic Logic Unit (ALU) Memories Example showing how to write
 Get Free notes at Module-I One s Complement: Complement all the bits.i.e. makes all 1s as 0s and all 0s as 1s Two s Complement: One s complement+1 SIGNED BINARY NUMBERS Positive integers (including zero)
Get Free notes at Module-I One s Complement: Complement all the bits.i.e. makes all 1s as 0s and all 0s as 1s Two s Complement: One s complement+1 SIGNED BINARY NUMBERS Positive integers (including zero)
Digital Systems and Binary Numbers
 Digital Systems and Binary Numbers ( 范倫達 ), Ph. D. Department of Computer Science National Chiao Tung University Taiwan, R.O.C. Spring, 2018 ldvan@cs.nctu.edu.tw http://www.cs.nctu.edu.tw/~ldvan/ Outline
Digital Systems and Binary Numbers ( 范倫達 ), Ph. D. Department of Computer Science National Chiao Tung University Taiwan, R.O.C. Spring, 2018 ldvan@cs.nctu.edu.tw http://www.cs.nctu.edu.tw/~ldvan/ Outline
D I G I T A L C I R C U I T S E E
 D I G I T A L C I R C U I T S E E Digital Circuits Basic Scope and Introduction This book covers theory solved examples and previous year gate question for following topics: Number system, Boolean algebra,
D I G I T A L C I R C U I T S E E Digital Circuits Basic Scope and Introduction This book covers theory solved examples and previous year gate question for following topics: Number system, Boolean algebra,
Arithmetic Logic Unit (ALU)
 Arithmetic Logic Unit (ALU) Introduction to Computer Yung-Yu Chuang with slides by Sedgewick & Wayne (introcs.cs.princeton.edu), Nisan & Schocken (www.nand2tetris.org) and Harris & Harris (DDCA) Let's
Arithmetic Logic Unit (ALU) Introduction to Computer Yung-Yu Chuang with slides by Sedgewick & Wayne (introcs.cs.princeton.edu), Nisan & Schocken (www.nand2tetris.org) and Harris & Harris (DDCA) Let's
Logic, Words, and Integers
 Computer Science 52 Logic, Words, and Integers 1 Words and Data The basic unit of information in a computer is the bit; it is simply a quantity that takes one of two values, 0 or 1. A sequence of k bits
Computer Science 52 Logic, Words, and Integers 1 Words and Data The basic unit of information in a computer is the bit; it is simply a quantity that takes one of two values, 0 or 1. A sequence of k bits
Chapter 5: Computer Arithmetic. In this chapter you will learn about:
 Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
EC2303-COMPUTER ARCHITECTURE AND ORGANIZATION
 EC2303-COMPUTER ARCHITECTURE AND ORGANIZATION QUESTION BANK UNIT-II 1. What are the disadvantages in using a ripple carry adder? (NOV/DEC 2006) The main disadvantage using ripple carry adder is time delay.
EC2303-COMPUTER ARCHITECTURE AND ORGANIZATION QUESTION BANK UNIT-II 1. What are the disadvantages in using a ripple carry adder? (NOV/DEC 2006) The main disadvantage using ripple carry adder is time delay.
